快速格林函数方法计算Chern绝缘体边界态
这篇博客整理一下如何利用格林函数方法来计算Chern绝缘体不同边界上的边界态. 在Chern Insulator边界态及Chern数计算这篇博客中提供了计算Chern绝缘体边界态的程序,但是...
BHZ模型Wilson loop计算
这里整理一下计算BHZ模型Wilson loop的代码. BHZ模型是最初学习拓扑时接触比较早的模型,前面也整理过如何计算BHZ模型的$\mathcal{Z}_2$拓扑不变量,但是其拓扑性质...
BBH Nested Wilson loop计算(Julia Version)
Python在执行一些操作的时候有点慢,这里就使用Julia写了一下Nested Wilson loop以及Wilson loop的计算程序。 Wilson loop这个计算没有什么好说的,...
秋
科研要搞,生活也要搞。 鉴于该网站分享的大都是学习笔记,作者水平有限,若发现有问题可以发邮件给我 yxliphy@gmail.com 也非常欢迎喜欢分享的小伙伴投稿
Andreev reflection and Fraction Josephson effect
最近正好有些空闲的时间,发现自己对拓扑中的一些理解并不深刻,正好借这个机会重新学习一下,加深自己对其中内容的理解,也能让自己之后的研究走的更远。 Andreev reflection要理解通...
Hubbard 模型平均场(简单介绍)
简单先整理一下Hubbard模型平均场处理的方法。 前言Hubbard模型作为凝聚态研究中许多有趣效应的出发点,具有很重要的研究价值。在固体物理最简单的处理中,就是忽略了电子与电子之间的相互...
Orbit effect and Zeeman effect in superconductor
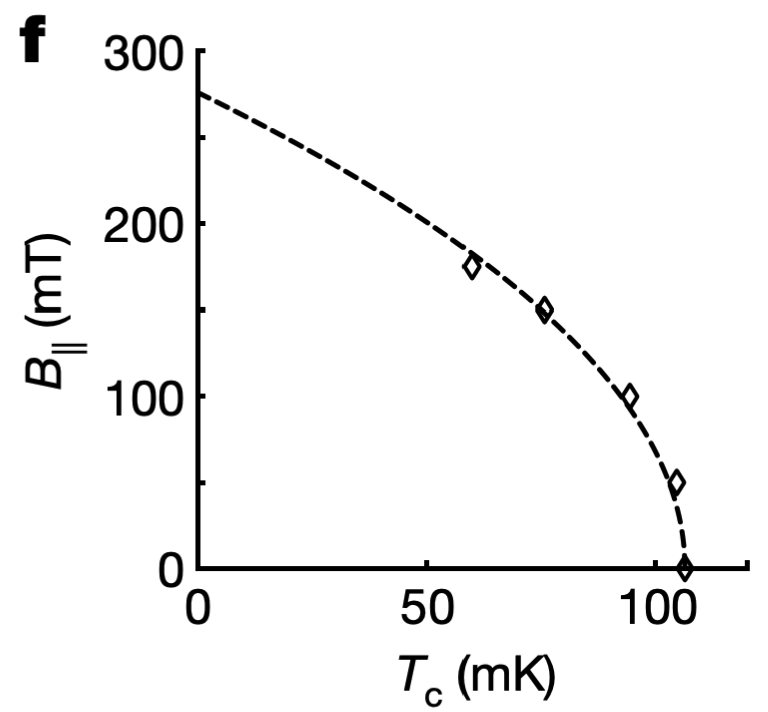
当外加磁场破坏超导电性时,轨道效应(orbital effect)是指磁场对电子的轨道运动产生的影响,这种效应导致超导态被破坏。具体来说,磁场通过影响电子的轨道运动,从而破坏超导电流的无阻流动能...
实验可测量与超导特征参数之间的关系(持续更新.......)
整理一下实验中如何测量超导一些特征参数。 超导相干长度与磁场关系 2\pi\xi^2=\frac{\phi_0}{B_{c\perp}},\quad \text{或者}\quad \xi=\...
常用量纲转换(持续更新.......)
整理物理量之间的转换关系。 为了将能量从毫电子伏特(meV)转换为温度(K),我们可以使用以下关系: E = k_B T其中,$E$ 是能量,$k_B$ 是玻尔兹曼常数,$T$ 是温度。 玻...
对称性约束响应系数
这里先用一个具体的例子来展示一下对称性是如何约束响应系数分量的。 这里来分析一下,在系统具有 $C_{2x}$ 对称性(即关于 $x$轴的二重旋转对称性)时,一阶电导率张量$\sigma_{...








![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)

