Yu-Xuan's Blog

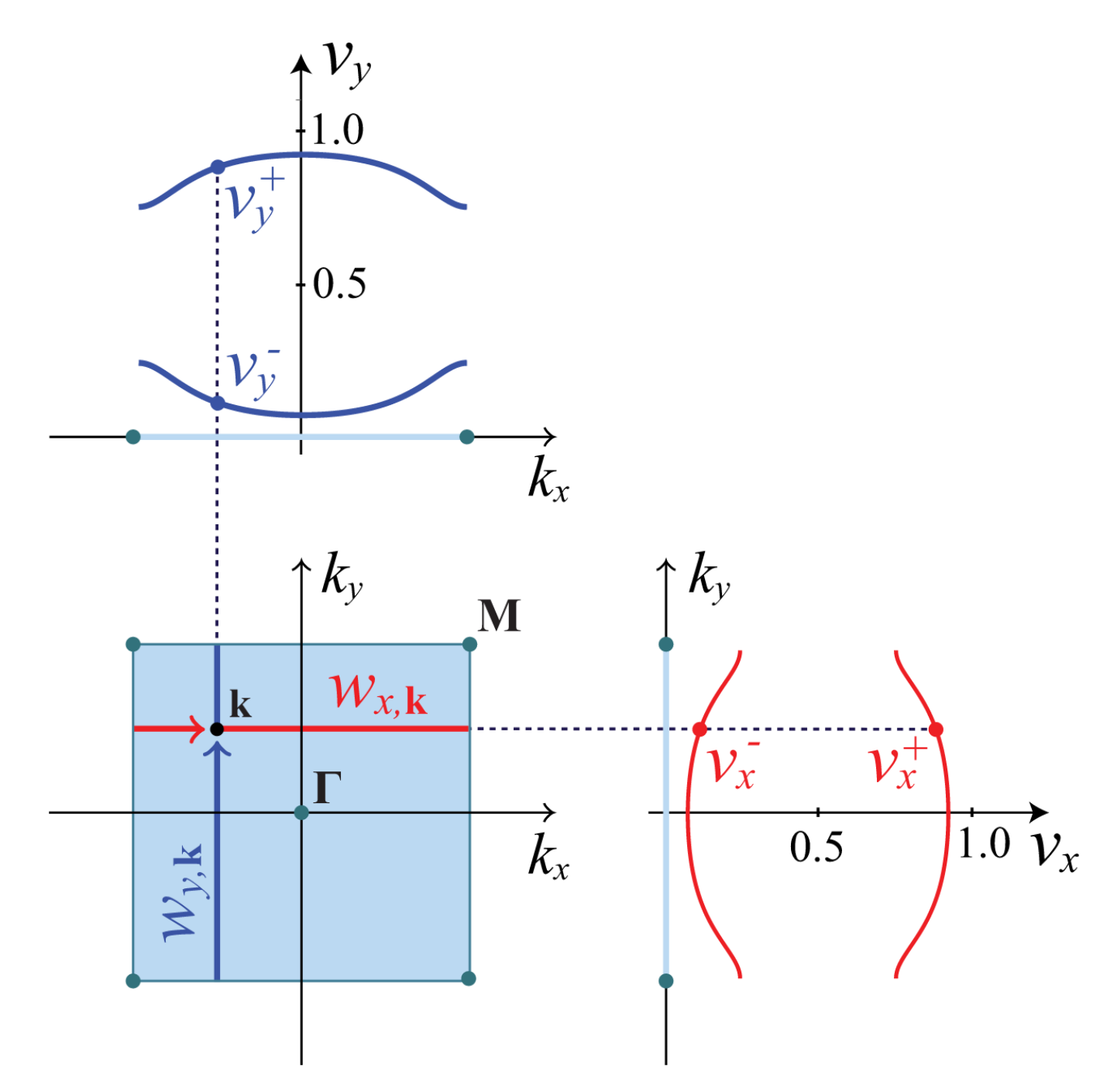
继续通过Wilson loop的理解，整理出如何计算Nested Wilson loop以及其物理含义。{:.info} Nested Wilson loop在计算高阶拓扑绝缘体的时候，其边界态被打开了能隙，那么此时通过Wilson loop就不再能鉴别体系的拓扑性质了。但是此时Wilson loop也会打开gap，因为文献中已经证明了体系的边界态和Wilson loop其实是等价的，所以这个时候可以对Wilson loop重新建立一个关于Wilson loop的体边对应关系，这也就关系着这里想要讨论的Nested Wilson loop。 仍然先考虑一个2D系统，其动量分别为$k_x,k_y$，而且其对应的Wilson loop都是有gap的，如下图所示 因为此时在$v_x=\frac{1}{2}$处存在Wannier gap，那么就可以将Wannier能带分成两个sector \begin{align} \nu^-_x &= \{\nu^j_x(k_y), \text{ s.t. } \nu^j_x(k_y) \text{ is below the Wannier gap} \}\nonumber \\ \nu^+_x &= \{\nu^j_x(k_y), \text{ s.t. } \nu^j_x(k_y) \text{ is above the Wannier gap} \}.\nonumber \end{align}在之前的Blog中提到过，因为在求解Wilson loop时的矩阵$G$是幺正的，所以它的本征值只有mod 1才是well defined，所以可以将这里通过gap分开的两个能带分别进行标记$\nu^-_x \in [0,1/2)$ and $\nu^+_x \in [1/2,1)$，那么就可以利用这些孤立的Wannier能带来分别构建其对应的投影算符 \begin{align} P_{\nu_x}&=\sum_{j=1}^{N_W}\sum_{R_x, k_y} \rvert \Psi^j_{R_x,k_y}\rangle \langle \Psi^j_{R_x,k_y}\rvert\nonumber\\ &=\sum_{j=1}^{N_W} \sum_{n,m=1}^{N_{occ}} \sum_\mathbf{k}...

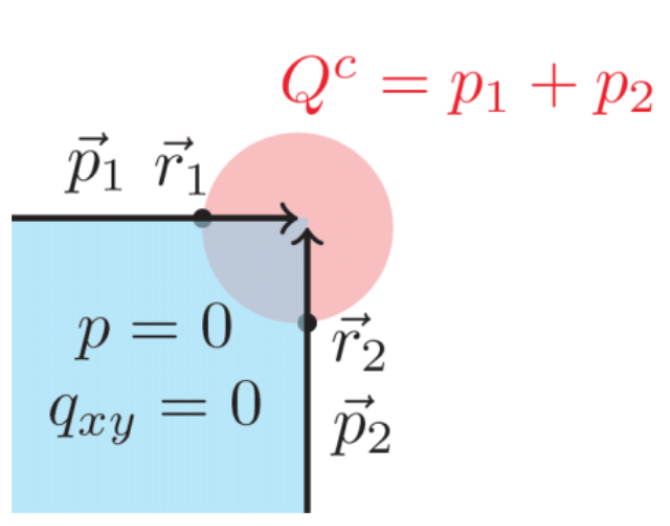
在计算发生边界拓扑相变的高阶拓扑绝缘体的时候, 有时候会遇到需要计算体系的边界极化, 其实也就是要在一个cylinder结构上计算其对应的Wilson loop, 并计算每个格点上对极化的贡献, 这里就先详细的整理一下理论背景, 后面给一个详细的例子来给出计算记过.{:.info} 边界极化首先考虑一个2D系统$\mathbf{k}=(k_x,k_y)$, 将其一个方向变换到实空间 c_{k,\alpha}\rightarrow c_{k_x,R_y,\alpha}此时二次量子化形式下的哈密顿量为 \begin{align} H = \sum_{k_x} c^\dagger_{k_x,R_y,\alpha} [h_{k_x}]^{R_y,\alpha,R'_y,\beta} c_{k_x,R'_y,\beta}, \label{eq1} \end{align}这里的$\alpha,\beta\in 1,\cdots N_{\rm orb}$为轨道指标, $R_y.R_y’\in 1\cdots N$则是$y$方向开边界之后的格点指标, 因为此时$x$方向仍然是周期的, 所以$k_x$还是一个好量子数, 此时计算需要的哈密顿量矩阵为 \begin{align} [h_{k_x}]^{R_y,\alpha,R'_y,\beta} = \sum_n [u^n_{k_x}]^{R_y,\alpha} \epsilon_{n,k_x} [u^{*n}_{k_x}]^{R'_y\beta}, \label{eq2} \end{align}这里的求和指标$n\in 1\cdots N_{\rm orb}\times N_y$. 如果二维系统的$x$方向和$y$方向都是周期的, 那么$h(k_x,k_y)$是有$N_{\rm orb}$个轨道的哈密顿量, 那么此时方程\eqref{eq2}中$h(k_x)$描述的就是一个具有$N_{\rm orb}\times R_y$个占据态能带的准1D体系, 与重学Wilson loop 中一样, 此时将哈密顿量进行对角化 \begin{align} H = \sum_{n,{k_x}} \gamma^\dagger_{n,{k_x}} \epsilon_{n,k_x}...

这里整理一下自己在重新学习高阶拓扑过程中，对Wilson loop以及相关内容的一个重新理解，也为后面理解Nested Wilson loop做一个铺垫。{:.info} 重学Wilson loop最近重读经典文献Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators，对Wilson loop其中的一些表示还有具体含义有了更多的理解，之前都只是参照公式进行计算，现在想重新整理一下具体的物理含义，而不是简简单单的计算一下。 位置算符在理解Berry位相的时候，除了通过参数空间中的演化来理解，在晶体中的电极化也是跟Berry位相有关的，实空间中极化问题的解决也就是现代极化理论。其中关键的一定就是将位置算符在周期系统中表示出来，首先在实空间中写出了位置算符，假设晶体中有$N$个原胞，每个原胞中的轨道数量为$N_{\rm orb}$，可以将位置算符表示为 \hat{x}=\sum_{R,\alpha}c^\dagger_{r,\alpha}\rvert 0\rangle e^{-i\delta_k(R+r_\alpha)}\langle 0\rvert c_{R,\alpha}这里的$\alpha\in1\cdots N_{\rm orb}$是轨道的指标，$R$则是原胞索引，$r_\alpha$是原胞中原子相对于原胞中心的位置，$\Delta_k=2\pi/N$，想要研究其在动量空间中的性质，进行傅立叶变换即可 \begin{array}{l}c_{R, \alpha}=\frac{1}{\sqrt{N}} \sum_{k} e^{-i k\left(R+r_{\alpha}\right)} c_{k, \alpha}, \\c_{k, \alpha}=\frac{1}{\sqrt{N}} \sum_{R} e^{i k\left(R+r_{\alpha}\right)} c_{R, \alpha}\end{array}这里的$k\in\Delta_k\cdot (0,1,\cdots,N-1)$，变换过程中利用周期边界条件 c_{R+N, \alpha}=c_{R, \alpha}...

在科研中我通常需要整理一些笔记,虽然也想用iPad来整理,但是排版上总是不尽人意,字写得也不好看,所以干脆就整理一个Latex模板专门整理学习笔记.这篇Blog就是将自己的这个模板分享出来,主要还是基于project-logbook进行了一些改造.{:.info} 这个笔记的模板就是将科研日志模板(Latex)这个模板修改了一下，将其中的一些环境块修改了，最后只保留了以note环境块，可以通过对其设置不同的颜色框来达到不同的目的，其实这个模板还是很简单的。 高亮块想要将一些文字高亮起来,这里使用了一个note环境来实现12\begin{note}{这里写title}{blue!50} \end{note} 12\begin{note}{Question}{red}\end{note} 在使用note环境的时候，第一个参数title就是用来设置高亮标题的,第二个参数则是控制高亮块的颜色。可以将重要的结论或者要注意的一些内容通过设置不同的颜色来进行标记。 想要设置不同的颜色，可以通过修改颜色blue!50产生不同的颜色块,从而来对不同的内容进行高亮标记。下面给一个我整理的笔记示例。 除此之外，还可以考虑给自己的笔记增加水印，可以在导言区加入下面的命令，这是用来加入一个图片水印，可以自己设计一个专属图片(我这里的图片由办公室段师姐提供，在此致谢)123456\makeatletter\@namedef{ver@everypage.sty}{9999/99/99}\makeatother\usepackage{everypage-1x}\usepackage[contents=DRAFT, color=red, opacity=0.2]{background}\backgroundsetup{scale=0.5, angle=45, opacity = 0.1, contents = {\includegraphics[width=\paperwidth, height=\paperwidth,...

平时在阅读文献或者组会讨论的时候总会有一些需要记录的内容，这里就修改了别人的一个模板，整理了一个适合自己的记录科研log的Latex模板。{:.info} Research-Log这是用来整理平时科研过程中自己的想法，和别人合作时各方的讨论结果以及问题整理的一个模版。平时在开组会活着与同学讨论过程中总会有一些想法，顺便可以整理记录，时间久了应该也能从中找出一些不错的点子。 我这里的模版是基于project-logbook进行了一些改造。它是一个英文版本，就是用来写科研日志的，我在这里进行了中文化，并对其中的一些环境进行了修改，对高亮色块的颜色配置进行了修改。 Meeting首先是Meeting环境1234\begin{Meeting}{会议日期}{main}%最后一个参数是作者id，用来标记这次会议是谁的想法这里是一次会议讨论内容的记录，主导者第一个作者，用mian来作为他的id。在这次讨论中有一个重要任务先要完成\hightodo{日期}{main}{这里是目前最优先要做的事情，这些事情都会被加入到最后的todo list 中 }\end{Meeting}这个环境块主要是用来整理一下会议或者讨论的记录，其中可以标记出会议的主导者。同时也能利用1\hightodo{日期}{main}{这里是目前最优先要做的事情，这些事情都会被加入到最后的todo list 中 }高亮出讨论中最重要，优先级最高的需要解决的问题。 Note(Think)这个环境块和Meeting没有太大本质上的区别，就是进行了颜色上的区分，可以给这个Note环境一个标题，用来提醒自己这个Note要说明什么问题。同样还有一个Think环境块，也只是修改了一下颜色而已。 这里还有一个lotodo，用来区别前面的hightodo，二者的颜色是不同的，代表了需要完成的事情的优先级是不同的，相当于是要高亮一下提醒自己需要做的事情，1\lowtodo{日期}{abc}{这里是目前次优先要做的事情 ，这些事情都会被加入到最后的todo list...

在进行数值计算的时候，对于较大的矩阵，有时候并不完全需要其所有的本征值，而只需要一定范围内的本征值即可，这里就整理一下如何利用Fortran来得到选定区间内的本征值{:.info}这里其实就是使用CHEEVX这个函数进行厄米矩阵对角化过程，具体使用实例可以参考这里，该函数的帮助文档在这里。 代码123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310! Author:YuXuan-Li! ...