Fortran结合MPI并行
该Bolg整理在Fortran用MPI编写并行程序，用在科学计算中速度提升肉眼可见， 代码解析先给一个完整的代码，是用来计算自旋极化率的，实际上在Fortran结合MPI并行计算自旋极化率中...
Fortran结合MPI并行计算自旋极化率
在之前的博客Julia的MPI并行计算极化率(重复Bilayer Two-Orbital Model of La$_3$Ni$_2$O$_7$ under Pressure)利用Julia计算了...
使用Latex进行文档对比并自动标记修改的内容
这里整理一下如何使用Latex自动整理出文档改动内容并进行标记，这个功能在我们给审稿人回复意见的时候非常有用。 前言通常在文章审稿的过程中，都需要根据审稿人的要求和问题对文章内容进行修改，常...
Julia的MPI并行计算极化率(重复Bilayer Two-Orbital Model of La$_3$Ni$_2$O$_7$ under Pressure)
这里将Julia的并行实操了一下,并行计算了自旋极化率,在通常的计算中这部分的计算量是非常大的,而使用Julia的宏@distributed我目前无法实现跨节点计算,这里就尝试用MPI并行实现跨...
Julia中MPI,@distributed,@threads三种并行方法的比较
最近折腾了一下Julia的并行操作，目前我了解到的有三种：MPI并行、@distributed、@threads，这里就用极化率的计算来对比一下三者的速度。 这里先单独列举一下三种并行方式在...
Julia的MPI并行
在之前搞计算的时候,虽然也用到了Julia的并行计算,但实现方法上并没有利用MPI,单速度上勉强也是够用的.最近遇到了计算量比较大的情形,此时如果可以在集群上多使用几个节点,多点CPU的话计算速...
超导中的约瑟夫森效应
关于超导约瑟夫森效应的笔记。 前言超导体除了抗磁效应在实际生活中有一定的应用之外，它还存在约瑟夫森(Josephson)效应，结构就是在两个超导体之间放置一个绝缘体，实验发现这个三明治结构在...
拓扑绝缘体(BHZ模型)边界态理论计算
解析求解拓扑绝缘体边界态 前言拓扑物态的研究已经成为了凝聚态研究中重要的一部分，我先不赘述与拓扑相关的基本知识了，其实在之前的量子几何张量与量子度规(1)这篇文章中，已经给出了基本的Berr...
超导中的金兹堡-朗道(Ginzburg–Landau )理论
在理解超导体的基本物理现象时，通过唯象的金兹堡-朗道理论(GL theory)是个不错的出发点，通过GL理论与电动力学中的麦克斯韦方程可以描述超导体的许多性质，其中之一就是超导完全抗磁性(Mei...
量子几何张量与量子度规-学习笔记
最近接触到了一个感兴趣的研究方向，其中涉及到了量子几何张量(Quantum geometry tensor)和量子度规(quantum metric)的概念，目前我正在学习过程中，整理了部分的内...
重学凝聚态拓扑(Class 2)
最近正好有些空闲的时间，发现自己对拓扑中的一些理解并不深刻，正好借这个机会重新学习一下，加深自己对其中内容的理解，也能让自己之后的研究走的更远。 Zero-dimensional quant...
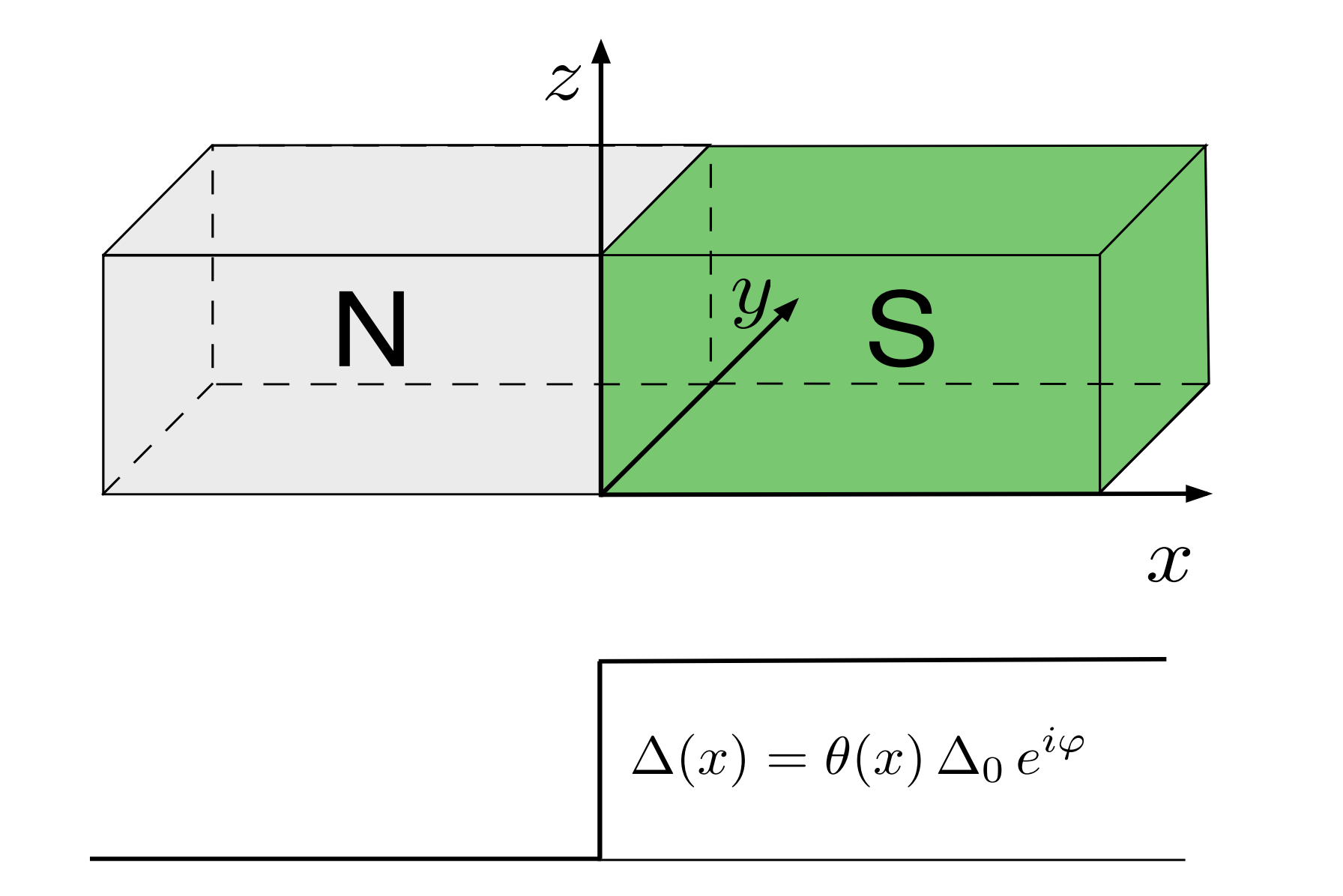
Andreev Reflection Note
Andreev反射作为超导独特的性质，在很多方面都有独特的现象，最近学习相关方面的知识，这里就先整理了一下。 Andreev Reflection考虑如上图所示的正常态-超导异质结，沿着$x$...
公告
欢迎关注公众号，有趣的内容也会在上面同步。 有密码的文章属于正在建设中或者没有通过验证的内容，若有需要可通过邮件联系。
![超导自由能泛函(Ginzburg–Landau)推导[非均匀配对]](/assets/images/SC/SC-Free.png)
