Kane Mele model zigzag 边界态的计算
接触量子自旋霍尔效应很久了,但是一直也都是在square lattice上做计算,
从来没有认真的在六角点阵上计算过拓扑的内容,正好最近在看文献的过程中需要在石墨烯机构上进行,
就从最基本的Kane-Mele 模型出发学习怎么在六角点阵上写出最近邻以及次近邻的哈密顿量。
{:.info}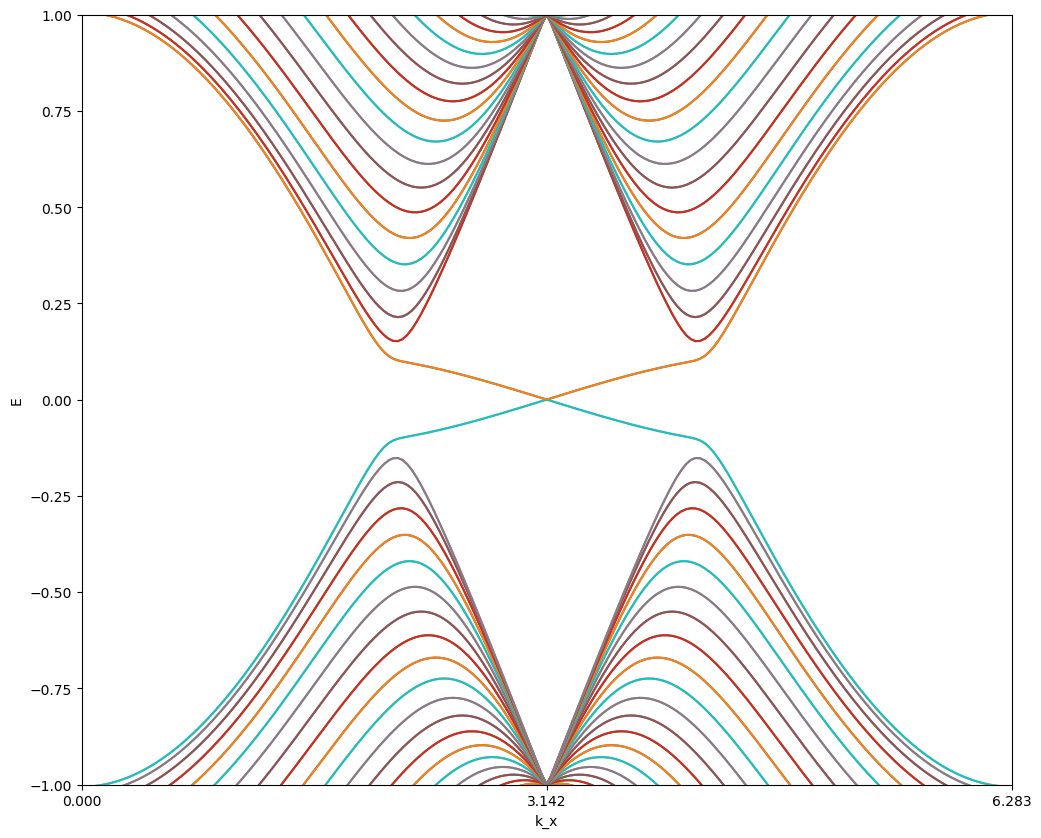
关于最近邻之间的hopping在前面石墨烯的边界态文章中已经仔细考虑过,包括cell的选取还有原子的编号,在这里。现在唯一的不同就是要考虑次近邻之间的hopping。在这里暂时并未考虑Rashbo自旋轨道耦合。
基本设定
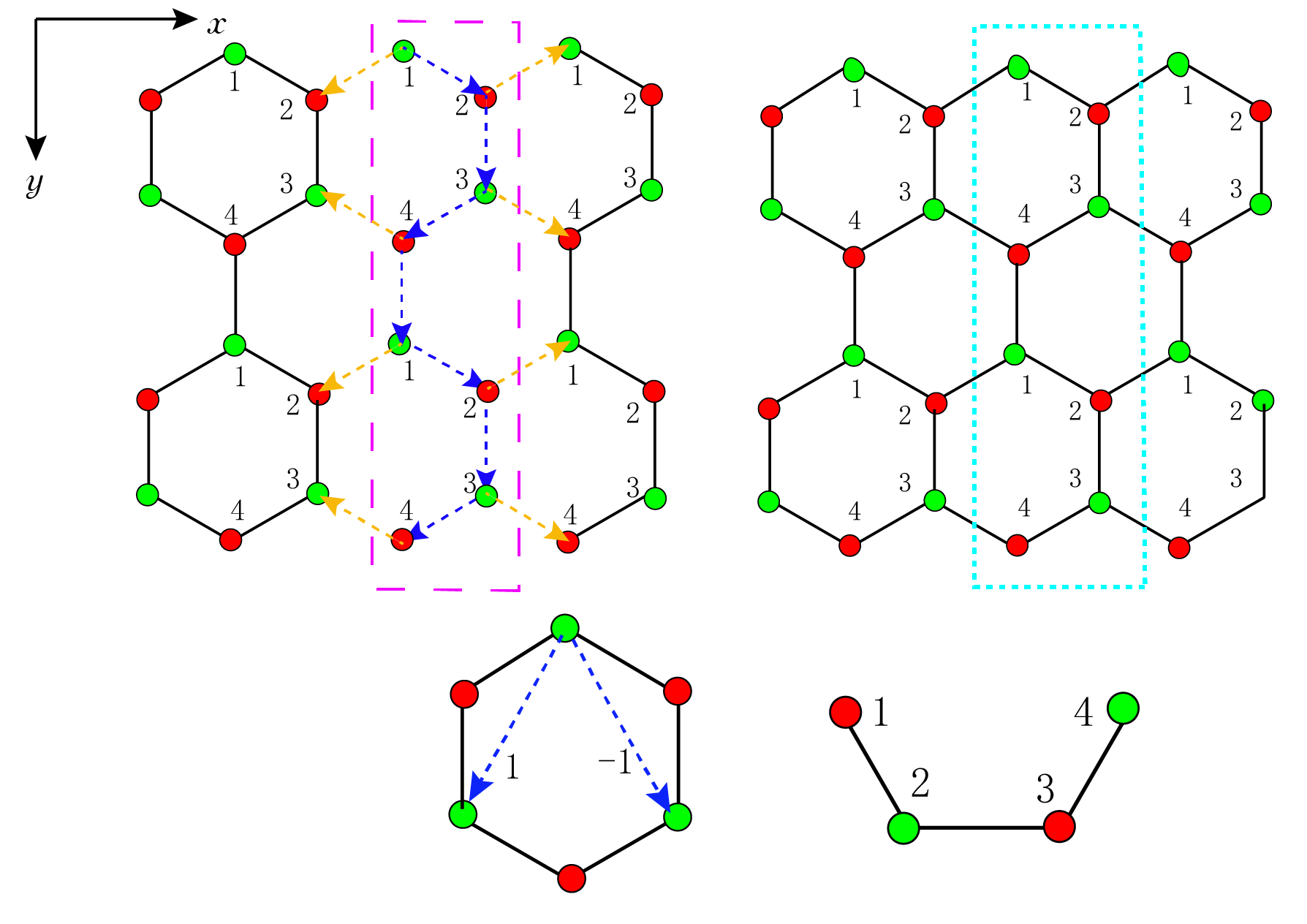
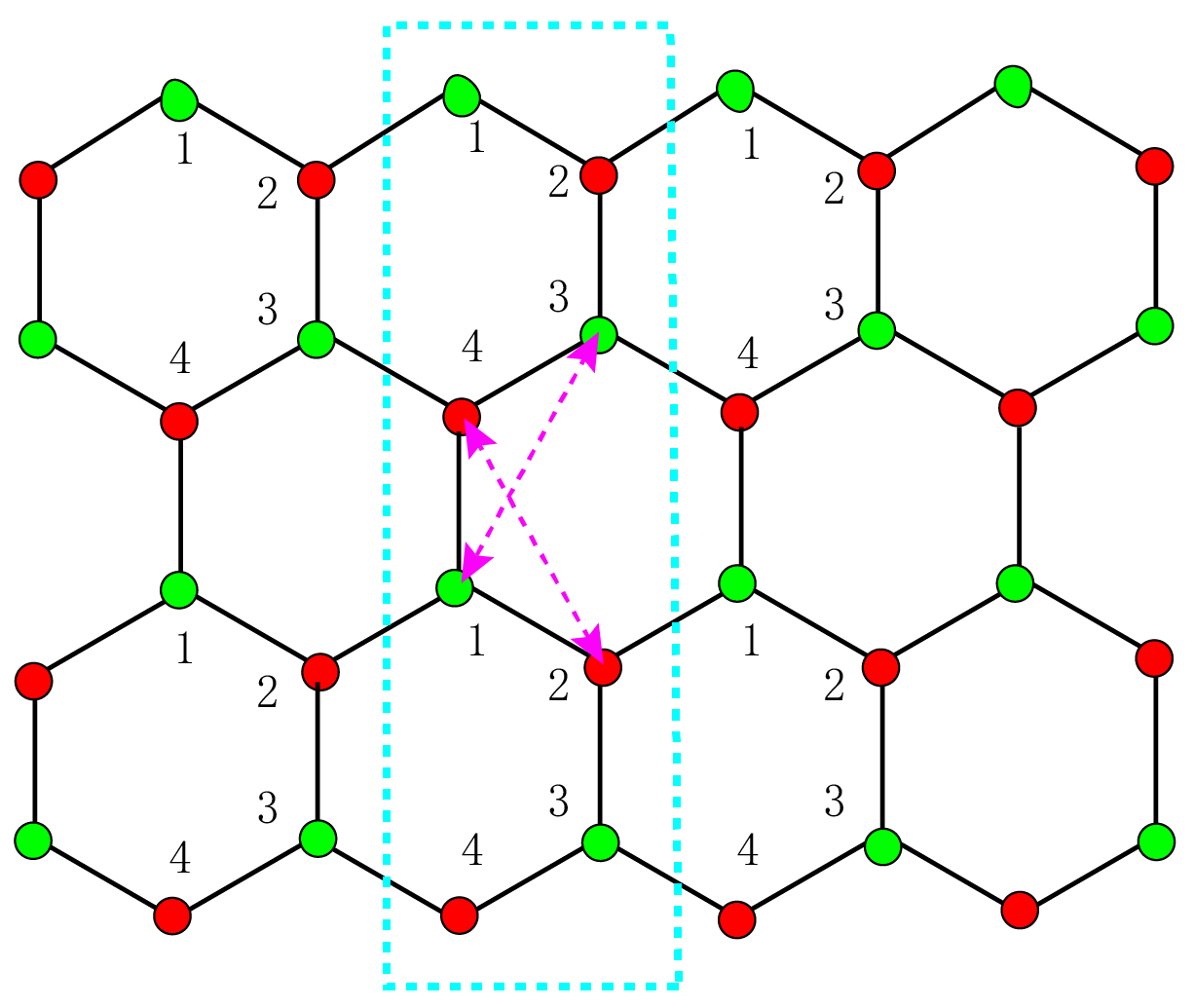
蓝色虚线框中是选择的一个大cell,在y方向是有限长度,在x方向是无限的,所以$k_x$是个好量子数,这种边界态叫zigzag;当x方向开边界,y方向无限长时的边界态叫armchair,可以参考这里。格点之间的hopping可以在一个大cell之内,可会存在大cell之间的hopping,在下面会逐一展示。关于Kane-Mele模型中的$v_{ij}$的示意如上图_hopping_蓝色箭头所示,当格点连线在hopping的右侧时$v_{ij}=-1$,在左侧时$v_{ij}=1$;将一个大cell划分成更小的周期重复结构,如上图右下图所示,并分别编号。第一张图所示的是最近邻hopping的选择。
与之前的Graphene模型相比较,这里是有两个自旋的,不过唯一的影响的只是第二项,对于上下自旋的不同相差一个符号,并不会对hopping的分析有影响。
次近邻hopping
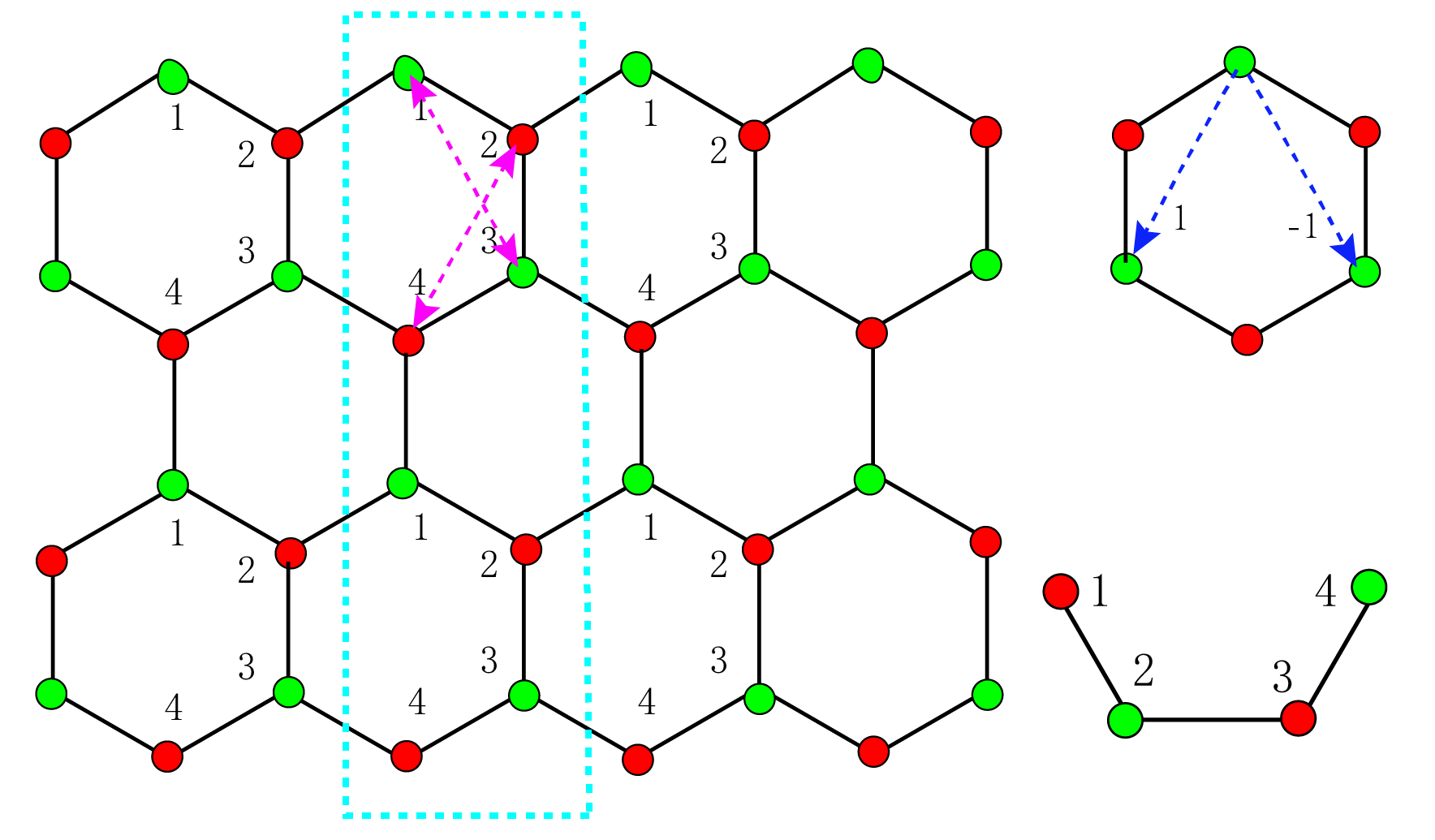
在虚线框中的是一个大cell,在右侧的是一个小cell,在写Hamiltonian的时候是以小cell为基本单元进行的。
首先可以看到,无论是边界上的小cell还是非边界上的小cell,都会具有如图中紫色虚线箭头所示的次近邻hopping,而且这些hopping是在同一个大cell内的。这种情况中格点连线都在hopping线的右端$v_{ij} = -1$,即就是对应$exp(-im*phi0)$,这里用$e^{i\phi_0}=\cos(\phi_0)+i\sin(\phi_0)$来更加方便的将模型中第二项的虚数因子吸收进来。此时的基矢选择为$\Psi^\dagger=(c^\dagger_{1\uparrow},c^\dagger_{1\downarrow},c^\dagger_{2\uparrow},c^\dagger_{2\downarrow},\dots,c^\dagger_{n\uparrow},c^\dagger_{n\downarrow})$,在这里补充一点,基矢的选择并不是只有这一种方式,同样可以选择$\Psi^\dagger=(c^\dagger_{1\uparrow},c^\dagger_{2\uparrow},\dots,c^\dagger_{n\uparrow},c^\dagger_{1\downarrow},c^\dagger_{2\downarrow},\dots,c^\dagger_{n\downarrow})$,只不过在构建矩阵的时候元素填充需要修改,不过结果是完全一样的,感兴趣可以验证一下。
1 | function spin(i::Int64)::Int64 |
 {:width=”400px”,:height=”495px”}
{:width=”400px”,:height=”495px”}
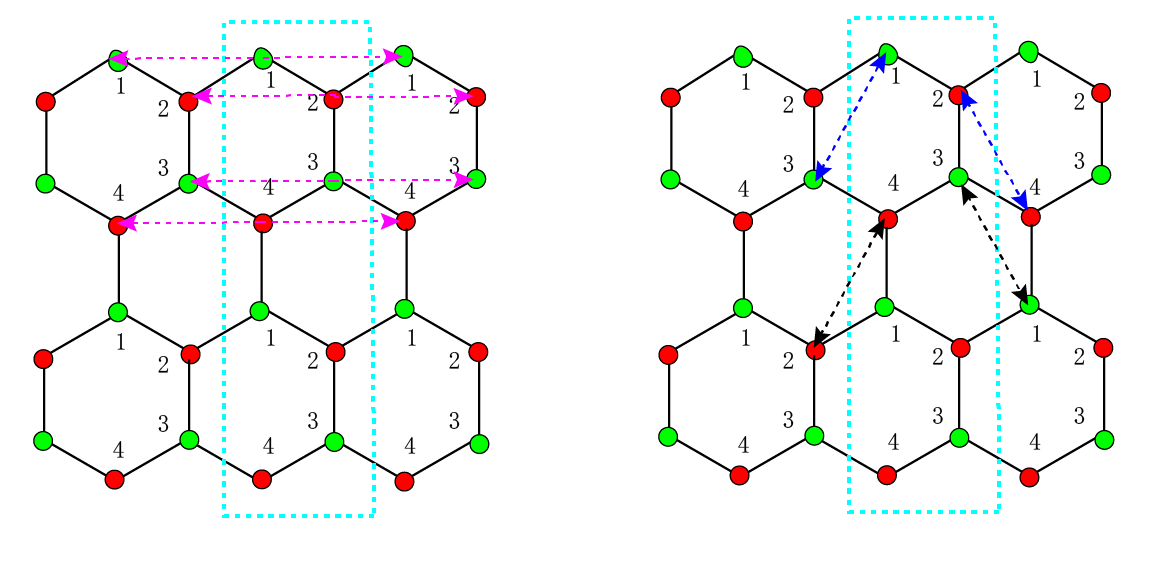
接下来考虑次近邻hopping连接到相邻的小cell之间的情况。从上图中可以看出,除了最后一个小cell之外,在大cell内剩余的小cell之间都会存在这种hopping。这种情况中格点连线都在hopping线的右端$v_{ij} = 1$,即就是对应$exp(im*phi0)$。
1 | for si = 1:2 |
上面所考虑的次近邻hopping都是在一个大cell内的(蓝色虚线),接下来考虑的次近邻是连接两个大cell的情况。
首先可以看到粉色箭头所示的次近邻hopping对于每一个小cell和每一个格点都是存在的,因为每个格点上这种形式的hopping同时存在向左和向右的情况,所以这两中hopping在同一个格点上是要相加的$2\cos(\phi_0)2\cos(k_x)$。下面右图所示的蓝色hopping线对于每一个小cell都是存在的,在这里需要注意一下,对于边界上的1,2位置上,只存在四个方向的次近邻,加上下图粉色的hopping,已经考虑了三个方向了,则只需要考虑剩下的一个方向hopping,即蓝色虚线所示。对于3,4格点,除了最下端的小cell的3,4格点不存在黑色虚线所示的hopping,其它*小cell中都存在,都是由6个方向的次近邻hopping。所以对于这些情况需要额外的考虑。
1 | # 对于水平方向的次近邻hopping,由于存在两个,向右hopping的vij=-1,向左hopping的vij=-1,它们是大cell之间hopping,相当与还是回到原来的格点位置,所以需要想这两种hopping加到一起 |
最近邻hopping
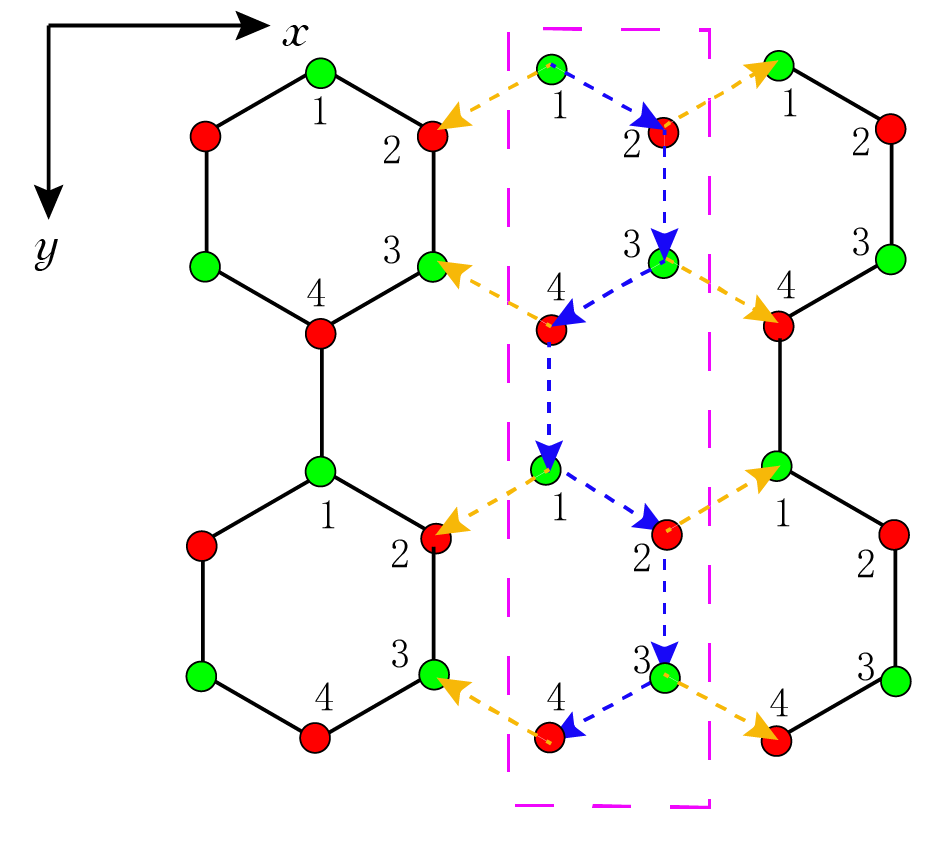 {:width=”400px”,:height=”495px”}
{:width=”400px”,:height=”495px”}
1 | function hn(kx::Float64,n::Int64)::Matrix{ComplexF64}# 最近邻hopping |
完整代码
1 | # import Pkg |
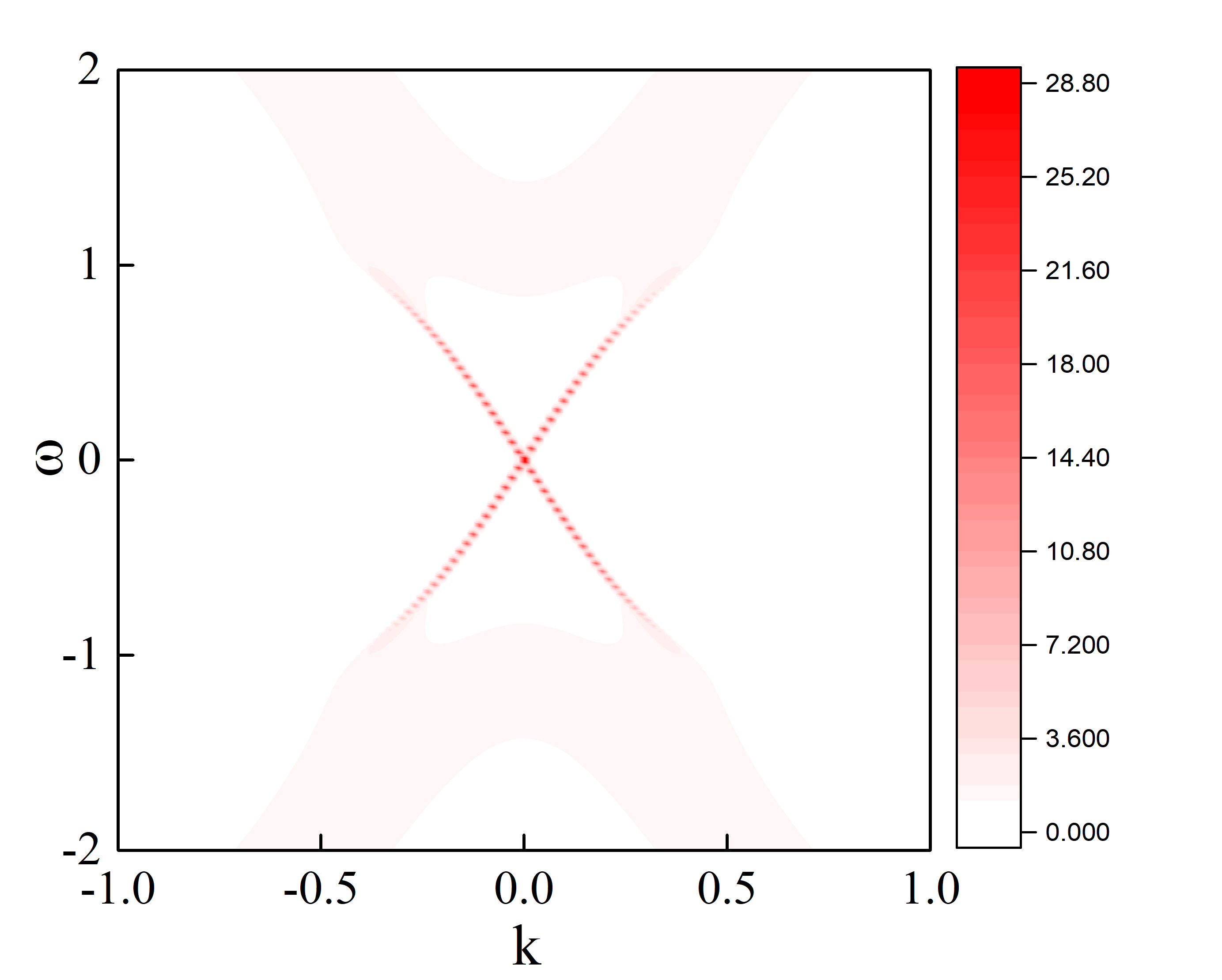
结果展示
 {:width=”400px”,:height=”495px”}
{:width=”400px”,:height=”495px”}
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |