有时候在文章中经常看到一些结果，会计算wave function profile，其实对应的也可以计算局域电子态密度。
局域电子态密度
关于局域电子态密度在可以自行去查看其含义和计算方法，这里的计算公式来自这里，文章中有具体的计算公式，但是其中牵扯到了BdG方程，这个不是我项讨论的东西，暂时先略过，想看BdG可以参考 Bogoliubovde Gennes Method and Its Applications，只要清楚它是怎么计算的。直接上代码进行演示。
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
!==========================================
module param
implicit none
integer xn,yn,ne,len2
parameter(xn = 30,yn = 30, len2=xn*yn)
integer,parameter::N = xn*yn*8
integer,parameter::up = xn
complex,parameter::im=(0.,1.)
real,parameter::pi = 3.14159265359
complex Ham(N,N)
integer bry(4,len2)
!------------------------------------------------------------------------------
real mu,tx,ty,delx,dely,ax,ay,m0,bcy,bcx
!-----------------LAPACK PACKAGE PARAM
integer::lda = N
integer,parameter::lwmax=2*N+N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork ! at least 2*N+N**2
integer lrwork ! at least 1 + 5*N +2*N**2
integer liwork ! at least 3 +5*N
integer info
end module param
!========== PROGRAM START ==========================
program sol
use param
integer m,l,i
!================ Physics memory allocate =================
external::fermi
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
Ham = (0,0) ! Hamiltonian initinal
! Boundary condition control
bcx = 0 ! zero is open boundary,one is periodic boundary conditions
bcy = 0 ! bcx is x direction boundary set,bcy is y direction set.
!------------------------------------------
m0 = 1.5
tx = 1.0
ty = 1.0
mu = 0.0
ax = 1.0
ay = 1.0
!=========== D(k) = D0 + D_x cos(k_x) + D_y cos(k_y) ============
del0 = 0
delx = 0.5
dely = -0.5
!------------------------
call matset()
call waveprofile()
call ldos()
stop
end
!===========================================================
subroutine waveprofile()
use param
integer ix,iy,i,m1,m2
real re
open(22,file="waveprof.dat")
do iy = 1,yn
do ix = 1,xn
i = (iy - 1)*xn + ix
re = 0
do m1 = 0,7
do m2 = -3,4
re = re + abs(Ham(i + m1*len2,xn*yn*4 + m2))**2.0
end do
end do
write(22,*)ix,iy,re
end do
end do
close(22)
end subroutine waveprofile
!===========================================================
subroutine matset()
use param
integer m,l,k1,k2
Ham = (0,0)
call diag()
call kinetic()
do m = 0,3
do l = 0,3
do k1 = 1,len2
do k2 = 1,len2
Ham(len2*4+len2*m+k1,len2*4+len2*l+k2) = -conjg(Ham(len2*m+k1,len2*l+k2)) !HOLE PART
end do
end do
end do
end do
call pair()
do k1 = 1,len2
do k2 = 1,len2
Ham(len2*4+k1,len2*2+k2) = -conjg(Ham(k1,len2*6+k2)) !(5,3) ---> (1,7)
Ham(len2*5+k1,len2*3+k2) = -conjg(Ham(len2+k1,len2*7+k2)) !(6,4) ---> (2,8)
Ham(len2*6+k1,k2) = -conjg(Ham(len2*2+k1,len2*4+k2)) !(7,1) ---> (3,5)
Ham(len2*7+k1,len2+k2) = -conjg(Ham(len2*3+k1,len2*5+k2)) !(8,2) ---> (4,6)
end do
end do
call ishermitian()
call eigsol()
return
end subroutine matset
!======================================================================
real function delta(x)
implicit none
real x
real::gamma = 0.005
delta = 1.0/3.1415926535*gamma/(x**2+gamma**2)
end function delta
!=========================== Local Density of State =============================
subroutine ldos()
use param
integer m,l,i
real s,E
real,external::delta
open(12,file="ldos.dat")
E = 0 ! zero energy Local Density of State
do m = 1,yn
do l = 1,xn
k = l + (m-1)*xn
s = 0
do i = 1,N
s = s + delta(w(i)-E)*(abs(Ham(k,i))**2+abs(Ham(k+len2,i))**2)&
+ delta(w(i)+E)*(abs(Ham(k+len2*6,i))**2+abs(Ham(k+len2*7,i))**2)
end do
write(12,*)m,l,s
end do
end do
close(12)
return
end subroutine ldos
!===========================================================
subroutine boundary()
! Transform lattice into a matrix index
use param
integer i,ix,iy
bry = 0
do iy = 1,yn ! y direction change
do ix = 1,xn ! x direction change
i = (iy-1)*xn + ix
bry(1,i) = i + 1 ! right hopping
if(ix.eq.xn)bry(1,i) = bry(1,i) - xn ! right boundary
bry(2,i) = i - 1 ! left hopping
if(ix.eq.1)bry(2,i) = bry(2,i) + xn ! left boundary
bry(3,i) = i + xn ! up hopping
if(iy.eq.yn)bry(3,i) = bry(3,i) - len2 ! upper boundary
bry(4,i)= i - xn ! down hopping
if(iy.eq.1)bry(4,i) = bry(4,i) + len2 ! lower boundary
enddo
enddo
end subroutine boundary
!================= diagonal block matrices ==============
subroutine diag()
use param
integer m,l,i
do m = 1,yn
do l = 1,xn
i = (m-1)*xn + l
Ham(i,i) = m0 + mu
Ham(len2+i,len2+i) = -m0 + mu
Ham(len2*2+i,len2*2+i) = m0 + mu
Ham(len2*3+i,len2*3+i) = -m0 + mu
end do
end do
!========= X =============================================
do l = 1,yn
do m = 2+(l-1)*xn,xn*l-1 ! Cannot consider left and right boundary
! (1,1) (a,up;a,up)
Ham(m,m+1) = -tx/2
Ham(m,m-1) = -tx/2
! (2,2) (b,up;b,up)
Ham(len2+m,len2+m+1) = tx/2
Ham(len2+m,len2+m-1) = tx/2
! (3,3) (a,down;a,down)
Ham(len2*2+m,len2*2+m+1) = -tx/2
Ham(len2*2+m,len2*2+m-1) = -tx/2
! (4,4) (b,down;b,down)
Ham(len2*3+m,len2*3+m+1) = tx/2
Ham(len2*3+m,len2*3+m-1) = tx/2
end do
end do
!========== X boundry ==========================
do m = 1,yn
! (1,1) (a,up;a,up)
Ham(m*xn,m*xn-(xn-1)) = -tx/2*bcx
Ham(m*xn,m*xn-1) = -tx/2
Ham(1+(m-1)*xn,1+(m-1)*xn+1) = -tx/2
Ham(1+(m-1)*xn,m*xn) = -tx/2*bcx
! (2,2) (b,up;b,up)
Ham(len2+m*xn,m*xn-(xn-1)+len2) = tx/2*bcx
Ham(len2+m*xn,m*xn-1+len2) = tx/2
Ham(len2+1+(m-1)*xn,1+(m-1)*xn+1+len2) = tx/2
Ham(len2+1+(m-1)*xn,m*xn+len2) = tx/2*bcx
! (3,3) (a,down;a,down)
Ham(len2*2+m*xn,m*xn-(xn-1)+len2*2) = -tx/2*bcx
Ham(len2*2+m*xn,m*xn-1+len2*2) = -tx/2
Ham(len2*2+1+(m-1)*xn,1+(m-1)*xn+1+len2*2) = -tx/2
Ham(len2*2+1+(m-1)*xn,m*xn+len2*2) = -tx/2*bcx
! (4,4) (b,down;b,down)
Ham(len2*3+m*xn,m*xn-(xn-1)+len2*3) = tx/2*bcx
Ham(len2*3+m*xn,m*xn-1+len2*3) = tx/2
Ham(len2*3+1+(m-1)*xn,1+(m-1)*xn+1+len2*3) = tx/2
Ham(len2*3+1+(m-1)*xn,m*xn+len2*3) = tx/2*bcx
end do
! ============= Y ======================
do m = xn+1,xn*(yn-1)
!(1,1) (a,up;a,up)
Ham(m,m+up) = -ty/2
Ham(m,m-up) = -ty/2
!(2,2) (b,up;b,up)
Ham(len2+m,len2+m+up) = ty/2
Ham(len2+m,len2+m-up) = ty/2
!(3,3) (a,down;a,down)
Ham(len2*2+m,len2*2+m+up) = -ty/2
Ham(len2*2+m,len2*2+m-up) = -ty/2
!(4,4) (b,down;b,down)
Ham(len2*3+m,len2*3+m+up) = ty/2
Ham(len2*3+m,len2*3+m-up) = ty/2
end do
!================= Y boundry ==============
do m = 1,xn
! (1,1)
Ham(m,m+up) = -ty/2
Ham(m,xn*(yn-1)+m) = -ty/2*bcy ! lower boundary
Ham(xn*(yn-1)+m,m) = -ty/2*bcy ! upper boundary
Ham(xn*(yn-1)+m,xn*(yn-1)+m-up) = -ty/2
! (2,2)
Ham(len2+m,m+up+len2) = ty/2
Ham(len2+m,xn*(yn-1)+m+len2) = ty/2*bcy
Ham(len2+xn*(yn-1)+m,m+len2) = ty/2*bcy
Ham(len2+xn*(yn-1)+m,xn*(yn-1)+m-up+len2) = ty/2
! (3,3)
Ham(len2*2+m,m+up+len2*2) = -ty/2
Ham(len2*2+m,xn*(yn-1)+m+len2*2) = -ty/2*bcy
Ham(len2*2+xn*(yn-1)+m,m+len2*2) = -ty/2*bcy
Ham(len2*2+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*2) = -ty/2
! (4,4)
Ham(len2*3+m,m+up+len2*3) = ty/2
Ham(len2*3+m,xn*(yn-1)+m+len2*3) = ty/2*bcy
Ham(len2*3+xn*(yn-1)+m,m+len2*3) = ty/2*bcy
Ham(len2*3+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*3) = ty/2
end do
return
end subroutine diag
!============= non-diagonal matrices =====================
subroutine kinetic()
use param
integer l,m
!========= A_xsink_x =================
do l = 1,yn
do m = 2+(l-1)*xn,xn*l-1
! (1,2)----->(5,6) (a,up;b,up)
Ham(m,len2+m+1) = -im*ax/2 ! This term under conjugate will be left hopping
Ham(m,len2+m-1) = im*ax/2
! (2,1)----->(6,5) (b,up;a,up)
Ham(len2+m,m+1) = -im*ax/2
Ham(len2+m,m-1) = im*ax/2
! (3,4)----->(7,8) (a,down;b,down)
Ham(len2*2+m,len2*3+m+1) = im*ax/2
Ham(len2*2+m,len2*3+m-1) = -im*ax/2
! (4,3)----->(8,7) (b,down;a,down)
Ham(len2*3+m,len2*2+m+1) = im*ax/2
Ham(len2*3+m,len2*2+m-1) = -im*ax/2
end do
end do
!========== Right and Left boundry ==========================
do m = 1,yn
! (1,2)
Ham(m*xn,len2+m*xn-(xn-1)) = -im*ax/2*bcx ! right boundary hopping towards right boundary
Ham(m*xn,len2+m*xn-1) = im*ax/2 ! right boundary hopping towards left
Ham(1+(m-1)*xn,len2+1+(m-1)*xn+1) = -im*ax/2 ! left boundary hopping towards right
Ham(1+(m-1)*xn,len2+m*xn) = im*ax/2*bcx ! left boundary hopping towards right boundary
! (2,1)
Ham(len2+m*xn,m*xn-(xn-1)) = -im*ax/2*bcx
Ham(len2+m*xn,m*xn-1) = im*ax/2
Ham(len2+1+(m-1)*xn,1+(m-1)*xn+1) = -im*ax/2
Ham(len2+1+(m-1)*xn,m*xn) = im*ax/2*bcx
! (3,4)
Ham(len2*2+m*xn,m*xn-(xn-1)+len2*3) = im*ax/2*bcx
Ham(len2*2+m*xn,m*xn-1+len2*3) = -im*ax/2
Ham(len2*2+1+(m-1)*xn,1+(m-1)*xn+1+len2*3) = im*ax/2
Ham(len2*2+1+(m-1)*xn,m*xn+len2*3) = -im*ax/2*bcx
! (4,3)
Ham(len2*3+m*xn,m*xn-(xn-1)+len2*2) = im*ax/2*bcx
Ham(len2*3+m*xn,m*xn-1+len2*2) = -im*ax/2
Ham(len2*3+1+(m-1)*xn,1+(m-1)*xn+1+len2*2) = im*ax/2
Ham(len2*3+1+(m-1)*xn,m*xn+len2*2) = -im*ax/2*bcx
end do
! ============= A_ysink_y(Tested is correct) ======================
do m = xn+1,xn*(yn-1)
!(1,2)
Ham(m,len2+m+up) = ay/2
Ham(m,len2+m-up) = -ay/2
!(2,1)
Ham(len2+m,m+up) = -ay/2
Ham(len2+m,m-up) = ay/2
!(3,4)
Ham(len2*2+m,len2*3+m+up) = ay/2
Ham(len2*2+m,len2*3+m-up) = -ay/2
!(4,3)
Ham(len2*3+m,len2*2+m+up) = -ay/2
Ham(len2*3+m,len2*2+m-up) = ay/2
end do
!================= Upper and Blower boundry ==============
do m = 1,xn
! (1,2)
Ham(m,len2+m+up) = ay/2
Ham(m,len2+xn*(yn-1)+m) = -ay/2*bcy
Ham(xn*(yn-1)+m,len2+m) = ay/2*bcy
Ham(xn*(yn-1)+m,len2+xn*(yn-1)+m-up) = -ay/2
! (2,1)
Ham(len2+m,m+up) = -ay/2
Ham(len2+m,xn*(yn-1)+m) = ay/2*bcy
Ham(len2+xn*(yn-1)+m,m) = -ay/2*bcy
Ham(len2+xn*(yn-1)+m,xn*(yn-1)+m-up) = ay/2
! (3,4)
Ham(len2*2+m,m+up+len2*3) = ay/2
Ham(len2*2+m,xn*(yn-1)+m+len2*3) = -ay/2*bcy
Ham(len2*2+xn*(yn-1)+m,m+len2*3) = ay/2*bcy
Ham(len2*2+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*3) = -ay/2
! (4,3)
Ham(len2*3+m,m+up+len2*2) = -ay/2
Ham(len2*3+m,xn*(yn-1)+m+len2*2) = ay/2*bcy
Ham(len2*3+xn*(yn-1)+m,m+len2*2) = -ay/2*bcy
Ham(len2*3+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*2) = ay/2
end do
return
end subroutine kinetic
! ================ Spuerconduct pair term =====================
subroutine pair()
use param
integer m,l
!==== ====== delta_X Term ===============
do l = 1,yn
do m = 2+(l-1)*xn,xn*l-1
!(1,7)
Ham(m,len2*6+m+1) = -delx/2
Ham(m,len2*6+m-1) = -delx/2
! (2,8)
Ham(len2+m,len2*7+m+1) = -delx/2
Ham(len2+m,len2*7+m-1) = -delx/2
! (3,5)
Ham(len2*2+m,len2*4+m+1) = delx/2
Ham(len2*2+m,len2*4+m-1) = delx/2
! (4,6)
Ham(len2*3+m,len2*5+m+1) = delx/2
Ham(len2*3+m,len2*5+m-1) = delx/2
end do
end do
!========== X boundry ==========================
do m = 1,yn
! (1,7)
Ham(m*xn,len2*6+m*xn-(xn-1)) = -delx/2*bcx ! right boundary hopping towards right boundary
Ham(m*xn,len2*6+m*xn-1) = -delx/2 ! right boundary hopping towards left
Ham(1+(m-1)*xn,len2*6+1+(m-1)*xn+1) = -delx/2 ! left boundary hopping towards right (1,5402)
Ham(1+(m-1)*xn,len2*6+m*xn) = -delx/2*bcx ! left boundary hopping towards right bpundary
! (2,8)
Ham(len2+m*xn,m*xn-(xn-1)+len2*7) = -delx/2*bcx
Ham(len2+m*xn,m*xn-1+len2*7) = -delx/2
Ham(len2+1+(m-1)*xn,1+(m-1)*xn+1+len2*7) = -delx/2
Ham(len2+1+(m-1)*xn,m*xn+len2*7) = -delx/2*bcx
! (3,5)
Ham(len2*2+m*xn,m*xn-(xn-1)+len2*4) = delx/2*bcx
Ham(len2*2+m*xn,m*xn-1+len2*4) = delx/2
Ham(len2*2+1+(m-1)*xn,1+(m-1)*xn+1+len2*4) = delx/2
Ham(len2*2+1+(m-1)*xn,m*xn+len2*4) = delx/2*bcx
! (4,6)
Ham(len2*3+m*xn,m*xn-(xn-1)+len2*5) = delx/2*bcx
Ham(len2*3+m*xn,m*xn-1+len2*5) = delx/2
Ham(len2*3+1+(m-1)*xn,1+(m-1)*xn+1+len2*5) = delx/2
Ham(len2*3+1+(m-1)*xn,m*xn+len2*5) = delx/2*bcx
end do
!=========== delta_Y Term =========================
do m = xn+1,xn*(yn-1)
!(1,7)
Ham(m,len2*6+m+up) = -dely/2
Ham(m,len2*6+m-up) = -dely/2
!(2,8)
Ham(len2+m,len2*7+m+up) = -dely/2
Ham(len2+m,len2*7+m-up) = -dely/2
!(3,5)
Ham(len2*2+m,len2*4+m+up) = dely/2
Ham(len2*2+m,len2*4+m-up) = dely/2
!(4,6)
Ham(len2*3+m,len2*5+m+up) = dely/2
Ham(len2*3+m,len2*5+m-up) = dely/2
end do
!================= Y boundry ==============
do m = 1,xn
! (1,7)
Ham(m,len2*6+m+up) = -dely/2 ! up
Ham(m,len2*6+xn*(yn-1)+m) = -dely/2*bcy ! down
Ham(xn*(yn-1)+m,len2*6+m) = -dely/2*bcy ! up
Ham(xn*(yn-1)+m,len2*6+xn*(yn-1)+m-up) = -dely/2 !down
! (2,8)
Ham(len2+m,m+up+len2*7) = -dely/2
Ham(len2+m,xn*(yn-1)+m+len2*7) = -dely/2*bcy
Ham(len2+xn*(yn-1)+m,m+len2*7) = -dely/2*bcy
Ham(len2+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*7) = -dely/2
! (3,5)
Ham(len2*2+m,m+up+len2*4) = dely/2
Ham(len2*2+m,xn*(yn-1)+m+len2*4) = dely/2*bcy
Ham(len2*2+xn*(yn-1)+m,m+len2*4) = dely/2*bcy
Ham(len2*2+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*4) = dely/2
! (4,6)
Ham(len2*3+m,m+up+len2*5) = dely/2
Ham(len2*3+m,xn*(yn-1)+m+len2*5) = dely/2*bcy
Ham(len2*3+xn*(yn-1)+m,m+len2*5) = dely/2*bcy
Ham(len2*3+xn*(yn-1)+m,xn*(yn-1)+m-up+len2*5) = dely/2
end do
return
end subroutine pair
!============================================================
subroutine ishermitian()
use param
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(16,file = 'hermitian.dat')
write(16,*)i,j
write(16,*)Ham(i,j)
write(16,*)Ham(j,i)
write(16,*)"===================="
close(16)
stop
end if
end do
end do
return
end subroutine ishermitian
!================================================================
subroutine eigsol()
use param
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','U',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','U',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file="mes.txt",status="unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
open(12,file="eigval.dat",status="unknown")
do m = 1,N
write(12,*)m,w(m)
end do
close(12)
return
end subroutine eigsol
程序中通过对矩阵的对角化同时计算了wave function profile 和 LDOS，通过文件名即可区分对应的结果。博主服务器上安装了intel Fortran，所以编译命令为ifort -mkl file-name.f90，-mkl是为了调用矩阵对角化的程序cheevd。局域电子态密度的结果如下：
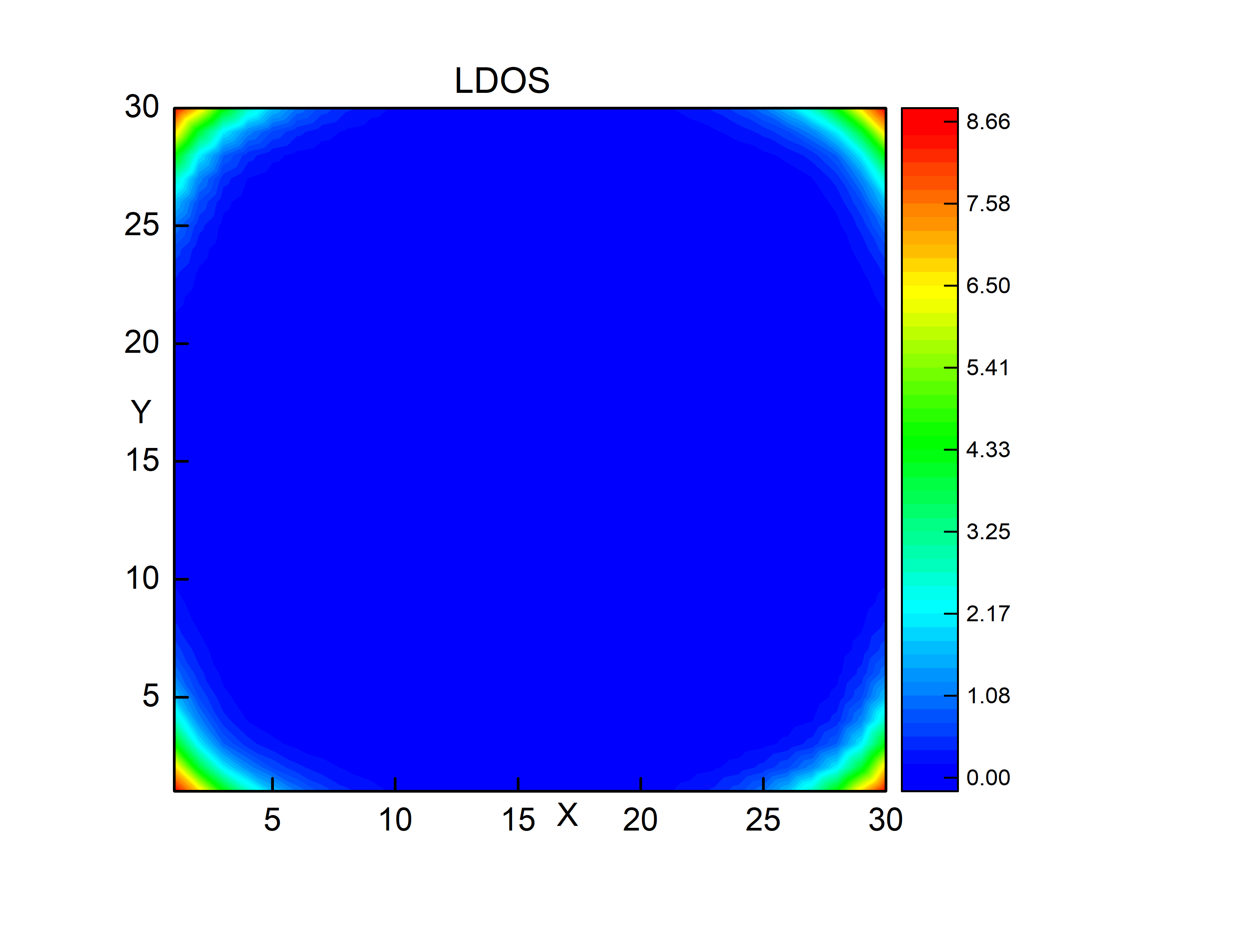代码计算LDOS的过程如下：
!======================================================================
real function delta(x)
implicit none
real x
real::gamma = 0.005
delta = 1.0/3.1415926535*gamma/(x**2+gamma**2)
end function delta
!=========================== Local Density of State =============================
subroutine ldos()
use param
integer m,l,i
real s,E
real,external::delta
open(12,file="ldos.dat")
E = 0 ! zero energy Local Density of State
do m = 1,yn
do l = 1,xn
k = l + (m-1)*xn
s = 0
do i = 1,N
s = s + delta(w(i)-E)*(abs(Ham(k,i))**2+abs(Ham(k+len2,i))**2)&
+ delta(w(i)+E)*(abs(Ham(k+len2*6,i))**2+abs(Ham(k+len2*7,i))**2)
end do
write(12,*)m,l,s
end do
end do
close(12)
return
end subroutine ldos
具体是如何计算LDOS的可以看这里，虽然这个文件不是关于现在这个模型的，但是实现过程都是完全类似的，可做参考。
wave function profile
先暂时说一些跟文章有关的内容：这是一个高阶拓扑超导的模型，在拐角处会产生Majorana corner state，它们对应的能量是0，关于零能这个证据，在矩阵对角化后从本征值就可以看到。而LDOS的结果也是表明了在四个拐角处的态密度比其它位置要大的多。 那么如何从波函数的直接得到跟上面类似的结果呢？关于矩阵对角化后的本征值和本征矢量问题，在p-wave 超导体Vortex中的Majorana zero mode的博客中的手册中找到详细的解释，里面同时又关于BdG方程的矩阵哈密顿量构建的方法。 既然corner state对应的能量是0，那么只需要关注零能本征值对应的本征矢量即可，这里一共会有8个零能本征值(具体的可以去搞明白这篇文献)，所以wave function profile的计算只需将8个零能本征值对应的波函数模方求和即可。
!===========================================================
subroutine waveprofile()
use param
integer ix,iy,i,m1,m2
real re
open(22,file="waveprof.dat")
do iy = 1,yn
do ix = 1,xn
i = (iy - 1)*xn + ix
re = 0
do m1 = 0,7
do m2 = -3,4
re = re + abs(Ham(i + m1*len2,xn*yn*4 + m2))**2.0
end do
end do
write(22,*)ix,iy,re
end do
end do
close(22)
end subroutine waveprofile
这就是通过Fortran实现的wave function profile 计算，结果如下：
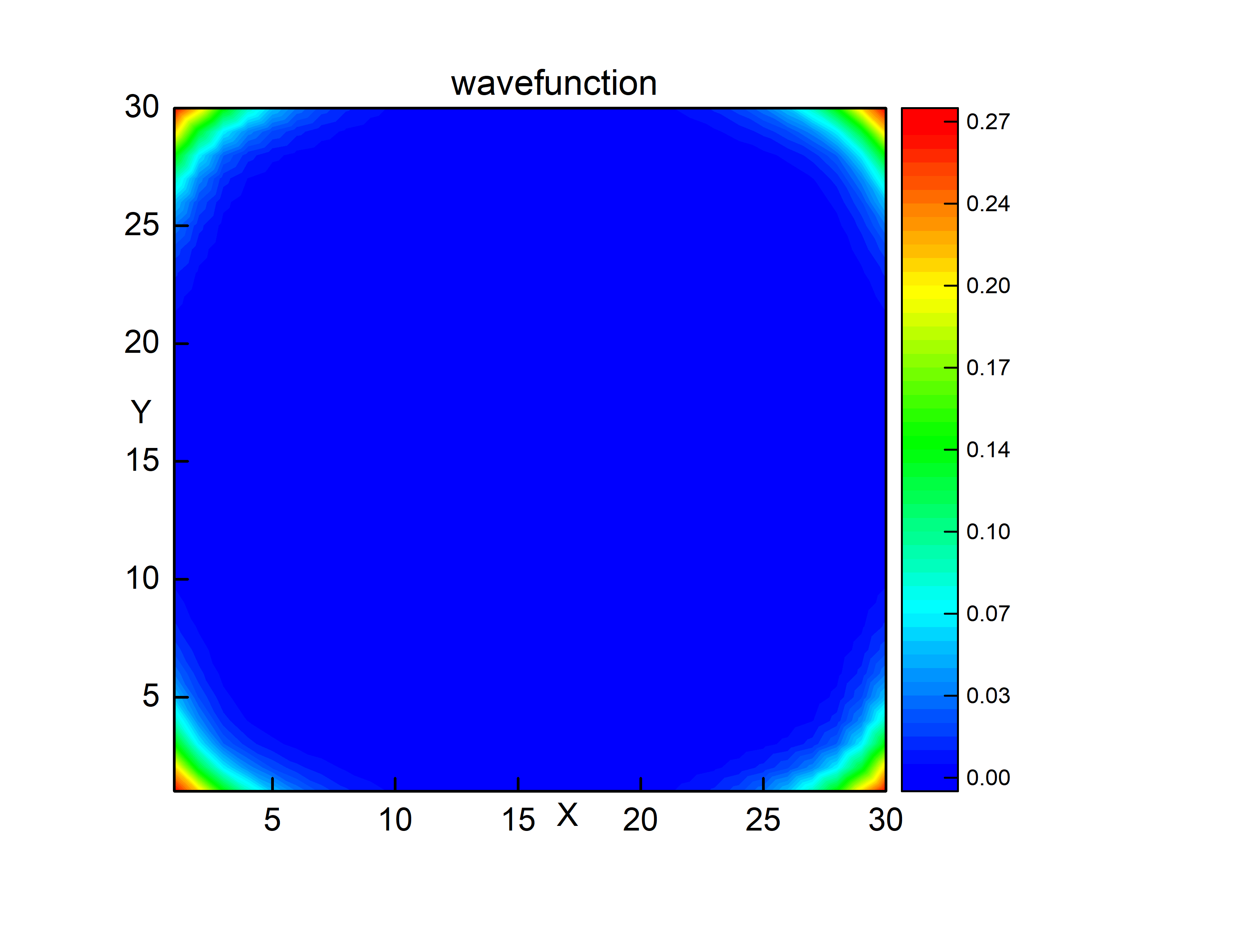这里计算的模型来自于这篇文章Majorana Corner Modes in a High-Temperature Platform
公众号
相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。
