在这篇博客中通过简单的SSH模型，来计算一下Winding Number这一拓扑不变量。虽然这个模型很简单，但是最近在学习Non-Hermitian的文章中，很多都是以这个模型为基础，研究非厄米体系的一些基本性质，其中也有通过计算非厄米系统的Winding Number来联系体系的拓扑性质。这里我就暂时不涉及非厄米的内容，因为我也只是对这个课题了解一点点内容，这里主要计算厄密SSH模型的Winding Number。

png

Winding Number

直观描述

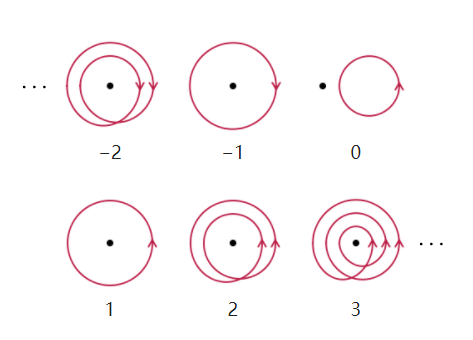
Winding number是指平面一条闭合的曲线以逆时针方向绕一点所转的圈数,正方向是逆时针,则这时候的Winding number是正数,如果是顺时针方向绕动的,那么Winding number就是负数.

png

数学表达

平面上的曲线可以通过参数方程来表示

\[x=x(t) \text { and } y=y(t) \quad \text { for } 0 \leq t \leq 1\]

如果在$t=0$和$t=1$的时候位置是相同的,那么在参数$t$变化的过程中就形成了一个闭合的曲线.这个问题同样可以放在极坐标空间中来处理

\[r=r(t) \text { and } \theta=\theta(t) \quad \text { for } 0 \leq t \leq 1\]

根据前面的假设,$t=0$与$t=1$位置相同,构成一个闭合的曲线,那么在极坐标空间中$\theta(0)$与$\theta(1)$之间则相差$2\pi$的整数倍

\[\text { winding number }=\frac{\theta(1)-\theta(0)}{2 \pi}\]

再次转换坐标系,在复平面上进行分析,直角平面上的两个分量分别看作是复平面上的实部和虚部,$z=x+\text{i} y=re^{i\theta}$

\[d z=e^{i \theta} d r+i r e^{i \theta} d \theta\] \[\frac{d z}{z}=\frac{d r}{r}+i d \theta=d[\ln r]+i d \theta\]

由于$\gamma$是闭合曲线,那么总的$\ln(r)$的改变等于0,所以积分$\frac{dz}{z}$就是i乘以总的$\theta$角的改变值,所以Winding Number又可以表示为

\[\frac{1}{2 \pi i} \oint_{\gamma} \frac{d z}{z}\]

SSH model

在这里我就不详细阐述什么是SSH模型了，简单的放一张示意图，向学习SSH模型的具体内容，可以去参考中的第一本书中，这本书讲的还是非常不错的。

png

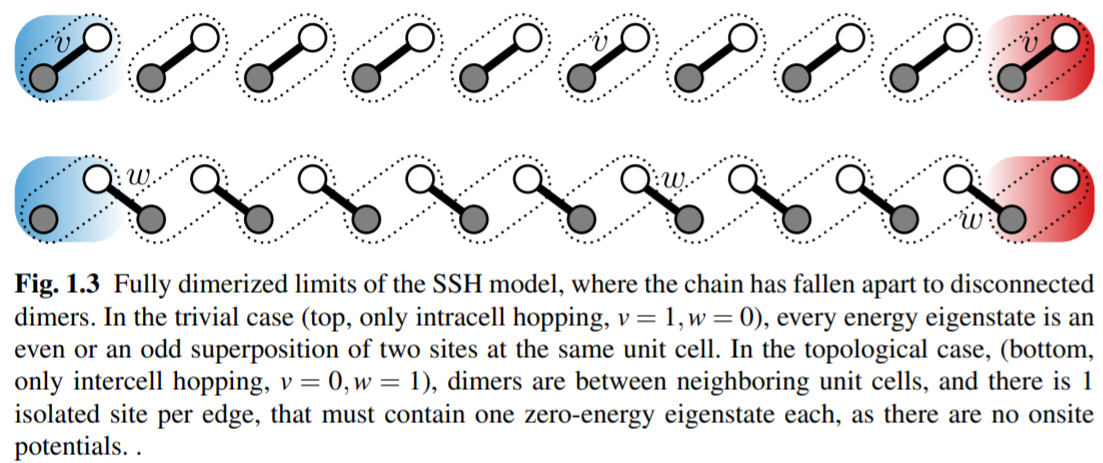
SSH 模型好玩的一点，其实就是每个元胞中包含两个不等价的原子，可以通过参数调节，来控制元胞内原子之间的hopping以及元胞间原子间的hopping，从而可以存在两种不同的结构，也就是如上图所示，可能在两边存在独立的边界态。

SSH模型的哈密顿量在动量空间中可以通过Pauli矩阵简单明了的表示出来 $H(k)=d_0(k)+\mathbf{d}(k)\mathbf{\hat{\sigma}},d_x=v+w\cos(k),d_y=w\sin(k),d_z=0$ $d_z=0$是由于系统具有手性(chiral)对称，可以把整个哈密顿量写成矩阵形式

png

接下来就是计算上面公式中的$v$，也就是Winding Number。首先对这个公式进行一下翻译，即如何将这种解析的公式转换成数值计算。

数值求导

$\frac{d\log(h(k))}{dk}\approx\frac{\log(h(k + \Delta k))-\log(h(k))}{\Delta k}$，在这里直接使用高等数学中导数的定义即可，因为在这里并不追求计算的精度，所以这个数值求导是很粗糙的，如果想追求精度也可以使用更加高精度的数值计算方法来计算函数在某一点上的导数(中心差商，二阶差商法等等)。

数值积分

接下来就是计算数值积分了，这里再说点题外话，计算函数的数值积分时，同样存在很多的方法，同样可以可以根据计算精度的要求，来选择合适的数值积分方法，比如欧拉法，三角形法等等。 $\int_a^bf(x)dx=\sum f(x)*\Delta x$，这是一个很粗糙的数值积分求和，精度非常低，但是因为这里只是想追求一个相对准确的结果，所以如果在计算的过程中，将间隔$\Delta x$取的较小的话，还是可以获取准确的结果，而这种粗糙的积分求和方式也是经常使用的，我曾在计算格林函数相关的一些内容时也是使用这个简单的方法，虽然精度比较差，但是主要的结果还是正确的。同样，想追求精度就可以自己改写这个数值积分的方法，利用高精度，以及速度更快的方式来计算。

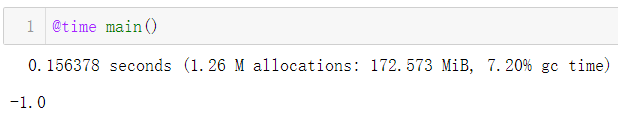
Winding Number计算

using LinearAlgebra
# =============================================
function matset(k::Float64)::Matrix{ComplexF64}
# 哈密顿量矩阵构建
    v::Float64 = 0.6
    w::Float64 = 1
    matrix = zeros(ComplexF64,2,2)
    matrix[1,2] = v + w*exp(-1im*k)
    matrix[2,1] = v + w*exp(1im*k)
    return matrix
end
# ===============================================
function main()
    dk1::Float64 = 1e-9 # 微分步长
    dk2::Float64 = 1e-5 # 积分步长
    wind::ComplexF64 = 0.0
    for k in -pi:dk2:pi
        h0 = matset(k)
        log0 = log(h0[1,2])
        
        hdk = matset(k + dk1)
        logk = log(hdk[1,2])
        
        wind = wind + (logk - log0)/dk1*dk2  # 数值微分与数值积分
    end
    return round(real(wind/(2*pi*1im)))
end