在学习格林函数的过程中,松原格林函数用来计算是很方便的,虽然它是用来处理有限温的问题,但是通过解析延拓之后,和零温下的格林函数的结果是相同的,而且相对于零温格林函数的计算,松原格林函数涉及到松原频率求和,在计算上面我觉得还是具有一定的简便性的,只需要扎实的掌握粒子分布函数和复变函数的留数定理之后,就可以快速的进行计算。
留数定理
设区域G的边界C为以分段光滑的简单闭合曲线,若除有限个孤立奇点$b_k,(k=1,2,3,…,n)$外,函数$f(z)$在G内单值解析,在G上连续,并且在C上$f(z)$没有奇点,则$\int_Cf(z)dz=2\pi i\sum_{k=1}^nRes[f(b_k)]$,$Res[f(b_k)]$即为函数$f(z)$在$b_k$处的留数,它等于$f(z)$在$b_k$的邻域内洛朗展开
\(f(z)=\sum_{l=-\infty}^{\infty}a^{(k)}_l(z-b_k)^l\) 中$(z-b_k)^{-1}$的系数$a_{-1}^{(k)}$。
留数计算理解
假设$z=b$是函数的一阶极点,则有$f(z)=a_1(z-b)^{-1}+a_0+a_1(z-b)+a_2(a-b)^2+…$,那么函数$f(z)$在$z=b$上的留数为$a_{-1}=lim_{z\rightarrow b}(z-b)f(z)$。从形式上来看,留数的计算就是在原函数$f(z)$中,将这个极点$z=b$抠去$(z-b)f(z)$,剩下的部分取$z=b$时候的值,就是这个函数在该奇点处的留数,这个简单的方法只是对于一阶极点而言,如果是高阶的极点,比如$z=b$是函数$f(z)$的$m$阶极点,则系数\(a_{-1}=\frac{1}{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}(z-b)^mf(z)|_{z=b}\)。
如果$z=b$是$f(z)$的一阶极点,结社函数$f(z)$可以表示为$\frac{P(z)}{Q(z)}$,$P(z),Q(z)$在$b$点及其邻域内解析,$z=b$是$Q(z)$的一阶零点,$Q(b)=0,Q’(z)\neq0,P(b)\neq0$,则可以得到$a_{-1}=\lim_{z\rightarrow b}(z-b)f(z)=\lim_{z\rightarrow b}(z-b)\frac{P(z)}{Q(z)}=\frac{P(b)}{Q’(b)}$
Bose/Fermi 分布函数的留数
Bose分布函数
玻色分布$n_B(z)=\frac{1}{e^{\beta z}-1}$,这个函数的极点为$z=\frac{2\pi i}{\beta}m,(m=0,\pm1,\pm2,…)$,利用上面一阶极点计算方法,$a_{-1}=\frac{1}{(e^{\beta z}-1)’|_{z=\frac{2\pi i}{\beta}m}}=\frac{1}{\beta}$,Bose分布函数的所有极点都是一阶极点且其留数为$\frac{1}{\beta}$
Fermi分布函数
Fermi分布$n_F=\frac{1}{e^{\beta z}+1}$,该函数极点为$z=\frac{(2m+1)\pi i}{\beta},(m=0,\pm1\pm2,…)$,利用相同的方法可以计算得到$a_{-1}=-\frac{1}{\beta}$,Fermi分布的所有极点同样也都是一阶极点其对应的留数为$-\frac{1}{\beta}$
松原求和计算
在利用松原格林函数计算时,会遇到对松原频率求和的计算,包括玻色频率($\omega=\frac{2m\pi i}{\beta}$)或者费米频率($\omega=\frac{(2m+1)\pi i}{\beta}$),下面就以一个实例来说明如何计算这种松原频率求和。
计算
\[S=-\frac{1}{\beta}\sum_m\frac{2\omega_q}{\omega_m^2+\omega_q^2}\frac{1}{ip_n+i\omega_m-\xi_p}=-\frac{1}{\beta}\sum_mf(i\omega_m)\]这里$\omega_m$是玻色频率,$p_n$是费米频率,$\omega_q,\xi_p$则是其它的变量,因为这两个不涉及到松原频率,所以把它们当作其他变量即可,不用特别对待。在利用复变函数留数定理的最大改变就是可以把一个闭合环路积分等价为对一些离散点函数值的求和,那么相应的我们同样可以把一系列离散点 求和变成一个闭合环路的积分,只不过在逆用留数定理的时候,由于求和函数(比如上面的$f(z)$)可能有它自己的极点,所以最后也只是将对Bose/Fermi分布函数极点上的求和,等价成对$f(z)$自身极点上的数值。可能突然这么说不太好理解,通过下面具体的计算就可以对上面的分析有一个更清晰的认识。
首先可以看到,S的求和是对所有的Bose频率操作的,那么可以先构造一个$R\rightarrow\infty$的闭合路径进行积分与求和之间的转换,即$I=\lim_{R\rightarrow \infty}\int\frac{dz}{2\pi i}f(z)n_B(z)$,对于这个半径趋向无穷大的环路积分,其结果是为0的,这一点是可以通过复变函数中约当引理可以证明,具体的可以参考复变函数中的内容,在这里就不进行更加详细的讨论。
下面将求和中的函数提取出来$f(z)=\frac{2\omega_q}{z^2-\omega_q^2}\frac{1}{ip_n+z-\xi_p}$,这个函数一共有三个极点:$z=\pm\omega_q,z=\xi_p-ip_n$,极点分布如下图所示
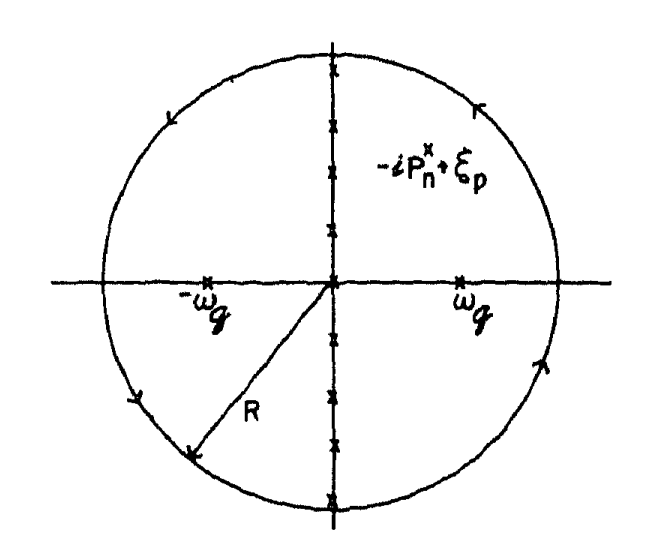
在虚轴上的是Bose分布函数的极点,其它的三个极点是来源于$f(z)$,接下来就是计算在不同的极点上对应的留数
Bose 频率:$z_m=\frac{2\pi m}{\beta}$,$R_i$ = $\frac{1}{\beta}f(i\omega_m)$
声子格林函数极点:$z_1=\omega_q$,$R_1$ = $\frac{n_B(\omega_q)}{ip_n-\xi_p+\omega_q}$,$z_2=-\omega_q$, $R_2$ = $\frac{2\omega_q}{-\omega_q-\omega_q}\frac{n_B(-\omega_q)}{ip_n-\xi_p-\omega_q}=\frac{n_B(\omega_q)+1}{ip_n-\xi_p-\omega_q}$
$n_B(-z)=-1-n_B(z)$
$z_3=\xi_p-ip_n$,$n_B(\xi_q-ip_n)=\frac{1}{e^{\beta(\xi_p-ip_n)}-1}=-\frac{1}{e^{\beta\xi_q}+1}=-n_F(\xi_q)$,$R_3=\frac{1}{ip_n-\xi_p+\omega_q}-\frac{n_F(\xi_p)}{ip_n-\xi_p-\omega_q}$
将这写所有极点上的留数加起来:$I=\frac{1}{\beta}\sum_mf(i\omega_m)+\frac{N_q+n_F(\xi_p)}{ip_n-\xi_p+\omega_q}+\frac{N_q+1-n_F(\xi_p)}{ip_n-\xi_p-\omega_q}$
前面说过,环路积分半径$R\rightarrow\infty$时积分结果为0,所以可以得到$-\frac{1}{\beta}\sum_mf(i\omega_q)=\frac{N_q+n_F(\xi_p)}{ip_n-\xi_p+\omega_q}+\frac{N_q+1-n_F(\xi_p)}{ip_n-\xi_p-\omega_q}=S$,到这里就得到了所需要计算的结果
参考
2.Many-Particle Physics(Third Edition)
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |