在$Z_2$拓扑不变量计算中,是通过一个比较直接的数值计算方法来对系统的$Z_2$拓扑不变量进行计算,而在学习能带拓扑的时候,最基本的理解都是通过电荷极化以及Wannier函数进行的,所以这里再利用Wannier Center的方法来计算体系的$Z_2$拓扑不变量,通过这个方法计算的时候,可以建立一个很清晰的物理图像,从而可以进一步加深对凝聚态物理中的拓扑有更深的理解。
Wannier Center
在学习在利用Wannier Center计算拓扑不变量的过程中,我想先对参考文章中的一些概念再做一些自己的理解。
Bloch Function
在周期势场中运动的电子,其波函数满足Bloch定理$\psi(\mathbf{r})=e^{i\mathbf{k}\mathbf{r}}u(\mathbf{r})$,其中$e^{i\mathbf{k}\mathbf{r}}$是调幅因子,而$u(\mathbf{r})$是函数的周期部分,即这一项就是满足和势场相同的周期性,也可以说这一项就是一个元胞内的波函数(cell function)。$u(\mathbf{r}+\mathbf{R})=u(\mathbf{r})$。
Wannier Function
在学习固体物理的时候,与Bloch函数相对应的就是Wannier函数,其中Bloch函数是个拓展性非常好的波函数,而相反的Wannier函数则是一个局域性非常强的波函数,其实这一点可以通过它们之间的联系看出来,因为它们二者之间互为其Fourier变化。那么通过量子力学中的动量空间与实空间的对应关系,自然也就可以有这一个清晰的图像对应。这里再强调一下Wannier函数的重要性,我在学习凝聚态拓扑的过程中了解到,很多电荷极化以及现代极化理论的理解和计算都离不开对Wannier函数。Bloch函数与Wannier函数之间的联系为: \(|k\alpha\tau\rangle=\frac{1}{\sqrt{N_{cell}}}\sum_je^{ik(R_j+\tau})|j\alpha\tau\rangle\) Bloch函数和Wannier函数都是完备基矢,都可以用作基矢来对任意的波函数进行展开,只要选取合适的展开系数即可
位置算符
文中首先定义了一个位置算符$\hat{X}=\sum_{j a \tau} \mathrm{e}^{-\mathrm{i} \tilde{\alpha} x_{x} \cdot\left(R_{j}+\tau\right)}|j \alpha \tau\rangle\langle j \alpha \tau|$,首先可以看到这是利用Wannier函数为基矢构成的位置算符。文章中指出,这个位置算符的位相中有实空间物理位置的物理意义,我做如下理解:先后先看到位相因子$\mathrm{e}^{-\mathrm{i} \tilde{\alpha} x_{x} \cdot\left(R_{j}+\tau\right)}$中含有$R_j$它代表了第$j$个元胞的位置$\tau$则代表的时元胞中其它原子的位置,如果选取的元胞不同,则$R_j$自然是不同的,这时候反映在这个位相上的值就不同,所以位相不同,则通过这个关系就可以将实空间位置与位相联系起来。
接下来又定义了投影算符,只不过这时候的投影算符是作用到特定的动量方向上的($k_x$ or $k_y$)
\[\hat{P}_{k_{y}}=\sum_{m \in o} \sum_{k_{x}}\left|\Psi_{m k_{x}k_y}\right\rangle\left\langle\Psi_{m k_{x} k_y}\right|\]这里的求和中的o代表的是对所有占据态本征矢量进行求和。接下来就是将位置算符与投影算符结合到一起,得到一个方向投影上的位置算符,即就是文章的公式(18),在这里存在一个$\delta$函数,所以当且仅当$k_x-k_x’=\delta k_x$的时候,这一项才不为零。而且在文章中也提到$\delta k_x=2\pi/N_xa_x,k_i=2\pi i/N_xa_x$,也就是在$k_x$方向上的离散动量,由于$\delta$函数的限制,所以才会有文章(19)式矩阵中$F_{i,i+1}$的索引表示,这个时候的$i$索引的是离散的动量$k_x$,因为这里是投影到$k_y$上的,所以将$k_x$当作了内部变化量,也就正好符合文章中提到的,将维度降低进行计算。
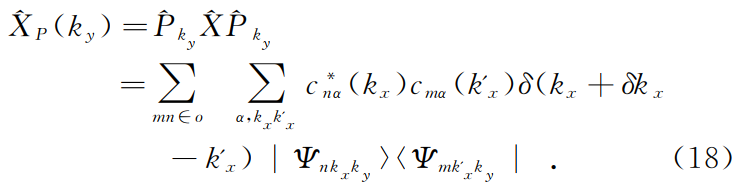
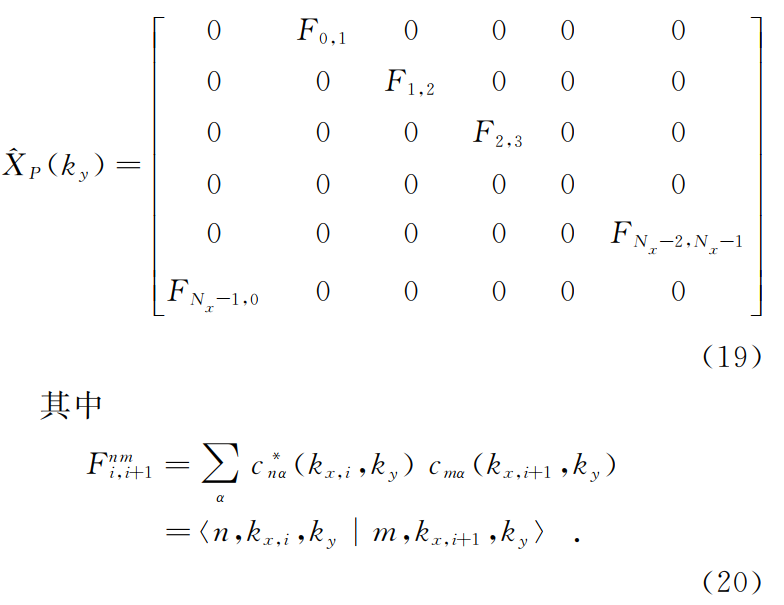
(19)矩阵构建的基矢为$|\Psi_{nk_xk_y}\rangle$,这些元素都出现在非对角线上是因为存在$\delta(k_x+\delta k_x-k_x’)$,从而限制了矩阵中元素的位置。
Wilson Loop
\(W(k_y)=F_{0,1}F_{1,2}F_{2,3}\dots F_{N_x-2,N_x-1}F_{N_x-1,0}\)
将(19)中的所有不为0的矩阵元按照顺序相乘,既可以得到由$k_x$的取值构成的一个闭合环路的$U(2N)$Wilson loop.
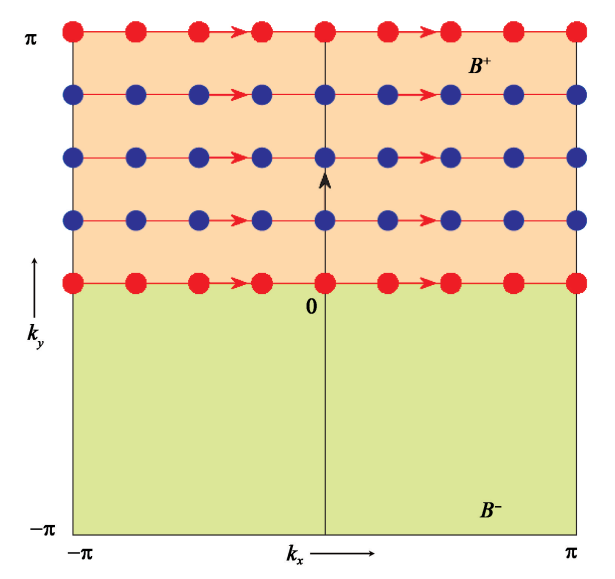
$F_{i,j}$的维度是$2N\times 2N$,即表示此时的占据态共有$2N$个
由于此时体系具有时间反演不变性,所以占据态的数目一定是偶数个,也就是说能带是二重简并的,故构成$F_{ij}$的矩阵也就是$2N\times 2N$大小的
这个矩阵$W(k_y)$的强大之处在于它的本征值和行列式是与环路上各个$k_x$点上的波函数的具体规范没有关系。这是一个很重要的性质,因为在前面计算chern数的文章中,我也曾遇到过规范选择的问题,但是我在那么没有提及这个问题,也是寻找了另外一种方法来计算chern数,而不是通过定义的方法直接计算的。所以这里构建的Wilson loop它的计算和规范选择无关,就具有很好的实用价值了。
在确定了$W(k_y)$矩阵之后,其本征值就是需要求解的量,假设本征值是$\lambda_m(k_y)=\lvert\lambda_m\rvert e^{i\phi(k_y)},(m=1,\dots,2N)$,本征值的位相$\phi(k_y)$即是等效一维系统占据态的瓦尼尔函数心(Wannier Center),而Wannier Center的演化则直接和体系的拓扑性质相联系,具体如何联系的可以参考后面的两篇文章。
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |