前面学习了chern数的计算,其中其实遇到了波函数规范选择的问题,这个在计算时间反演不变系统的$Z_2$拓扑不变量的时候也会遇到,暂时我对这个规范问题也没有很好的理解,正好也通过计算$Z_2$拓扑不变量来对规范问题进行更进一步的了解,这里只是单纯的学习如何计算$Z_2$。
计算方法
首先介绍一下我学习的计算$Z_2$ 拓扑不变量的方法,主要参考了这个PPT中的计算方法。如果网址打不开,可以在这里下载。我在这里只是简单的展示一下如何用代码计算拓扑不变量,而对于ppt中的计算方法还在进一步理解中,也非常欢迎对这方面比较熟悉的人,可以和我交流交流,让我对这部分内容有一个更加深入的了解。
BHZ 模型$Z_2$拓扑不变量计算
在这里,我就一比较熟悉的BHZ模型为例,来计算一下其$Z_2$拓扑不变量。在这里首先对ppt中的公式运用做一些说明。
首先,熟悉chern number计算的话,肯定知道我们是要对占据态能带进行拓扑不变量的计算,在第10张ppt中 \(U_{\mu}=\det(\langle u_m(\mathbf{k})|u_n(\mathbf{k} + \Delta\mu)\rangle)\) 这里的$|u\rangle$代表的都是占据态的本征矢量,所以如果求解得到哈密顿量对应的本征值和本征矢量后,假设此时化学势为0,那么应该选取的就是能量小于零对应的本征矢量来进行计算。这里因为是存在时间反演对称,所以如果本征值一定会成对出现,即存在简并态(两个本征矢量具有相同的本征值),关于相同的本征值有两个,这一点可以在计算的时候明确得到。
假设计算得到一个本征值为$E_1$,那么对应的一定存在另外一个本征值$E_2$,满足$E_1 = E_2$,但是这两个本征值对应的本征矢量是不同的。所以上面的表 达式中计算的矩阵行列式,这个矩阵就是由这两个简并的本征态构成的。而$\Delta \mu$则是代表在$k_x$或者$k_y$方向上有一个增量。我在看ppt中的这个行 列式计算的公式的时候,是觉得它有一些让人疑惑的地方。还是以第十张ppt中的计算公式$U_{\mu}=\det(\langle u_m(\mathbf{k})|u_n(\mathbf{k} + \Delta\mu)\rangle)$,在这个公式中应该写出$U_\mu=U_\mu(\mathbf{k})$,这样就可以很自然的可以和下面计算贝利联络以及贝利曲率的公式相互联系起 来。如果作为初学者,可能会对这个地方有一个小的疑惑。在这里再进一步把这些角标说的更加清楚一些,计算公式中的$m,n$其实就是两个相同本征值对应的两 个不同的本征矢量。所以如果系统存在时间反演对称性,那么本征值成对出现,所以在对角化哈密顿量之后,两个占据态的本征值对应两个两个不同的本征矢量(价带波函数),这 也就是这里$m,n$索引的对象(分别对应的是两个本征值的本征矢量),所以这是一个2*2的矩阵,可以通过简单的方法求得其行列式,关于行列式的求解,可以在程序中去查找。
在最后利用Berry联络求解拓扑数的时候的公式为
\[n(k_l)=\frac{1}{2}(\left[\Delta_\nu A_\mu-\Delta_\mu A_\nu\right]-F(k_l))\]将这个公式翻译成差分形式之后也就是
\[\Delta_\nu A_\mu=A_{\mu+\nu}-A_\mu\qquad\Delta_\mu A_\nu=A_{\nu+\mu}-A_\nu\]这里$A_\mu(k_l)=\textrm{Im}\log\left[ U_\mu(k_l)\right]$,那么相应上面的公式其实也就是对$U_\mu(k_l)$的差分.这个形式在代码里面也可以很清楚的看明白。
在计算$Z_2$的过程中,需要用到多个方向上增量的本征矢量,包括:$(k_x,k_y),(k_x + \Delta k_x,k_y),(k_x+\Delta k_x,k_y + \Delta k_y),(k_x, k_y+\Delta k_y)$,这其实也就对应着第11张ppt中的示意图中的$u_1,u_2,u_3,u_4$。这里的$u_i$对应的都是简并的本征态,所以也就有了相应的对矩 阵求行列式的操作。具体是如何构成这个矩阵的,即就是上面所说的利用两个简并本征矢量来构成。
Julia
using LinearAlgebra
function ham(kx::Float64,ky::Float64)::Matrix{ComplexF64}
# BHZ模型
A::Float64 = 0.3645/5
B::Float64 = -0.686/25
C::Float64 = 0
D::Float64 = -0.512/25
M::Float64 = -0.01
matrix = zeros(ComplexF64,4,4)
varepsilon = C - 2*D*(2 - cos(kx) - cos(ky))
d3 = - 2*B*(2 - (M/2/B) - cos(kx) - cos(ky))
d1d2 = A*(sin(kx) + 1im*sin(ky))
matrix[1, 1] = varepsilon + d3
matrix[2, 2] = varepsilon - d3
matrix[1, 2] = conj(d1d2)
matrix[2, 1] = d1d2
varepsilon = C - 2*D*(2 - cos(-kx) - cos(-ky))
d3 = - 2*B*(2 - (M/2/B) - cos(-kx) - cos(-ky))
d1d2 = A*(sin(-kx) + 1im*sin(-ky))
matrix[3, 3] = varepsilon + d3
matrix[4, 4] = varepsilon - d3
matrix[3, 4] = d1d2
matrix[4, 3] = conj(d1d2)
return matrix
end
# ==============================================================================
function detcal(a1,b1,a2,b2)
# 计算行列式
x1 = dot(a1',b1)
x2 = dot(a2',b2)
x3 = dot(a1',b2)
x4 = dot(a2',b1)
return x1*x2 - x3*x4
end
# ===============================================================
function main()
dk::Float64 = 0.05
Z2::Float64 = 0.0
Ux::ComplexF64 = 0.0 + 0im
Uy::ComplexF64 = 0.0 + 0im
Uxy::ComplexF64 = 0.0 + 0im
Uyx::ComplexF64 = 0.0 + 0im
F::Float64 = 0.0
A::Float64 = 0.0
for kx in -pi:dk:0
for ky in -pi:dk:pi
h = ham(kx,ky)
val,vec = eigen(h)
vc1 = vec[:,1]
vc2 = vec[:,2]
# ----------------------------
hkx = ham(kx + dk,ky)
val,vec = eigen(hkx)
vkx1 = vec[:,1]
vkx2 = vec[:,2]
# ----------------------------
hky = ham(kx,ky + dk)
val,vec = eigen(hky)
vky1 = vec[:,1]
vky2 = vec[:,2]
# -------------------------------------------
hkxky = ham(kx + dk,ky + dk)
val,vec = eigen(hkxky)
vkxky1 = vec[:,1]
vkxky2 = vec[:,2]
# -------------------------------------------
Ux = detcal(vc1, vkx1, vc2, vkx2)
Uy = detcal(vc1, vky1, vc2, vky2)
Uxy = detcal(vky1, vkxky1, vky2, vkxky2)
Uyx = detcal(vkx1, vkxky1, vkx2, vkxky2)
# --------------------------------------------
F = imag(log(Ux*Uyx*conj(Uxy)*conj(Uy)))
A = -imag(log(Ux)) + imag(log(Uyx)) + imag(log(conj(Uxy))) -imag(log(conj(Uy)))
Z2 = Z2 + (A - F)/(2.0*pi)
end
end
return mod(Z2,2)
end
# ====================================================================
@time main()
Mathematica
最近正好又回想起来要利用这个方法来计算$Z_2$拓扑不变量,也就用Mathematica也写了一个版本,不过对于这种循环的程序,直接改写成Mathematica的代码,样子又丑,运行速度还不怎么滴,所以我也只是拿来练练手,熟悉了一下方法,并没有带代码进行函数式编程的改写,毕竟函数式编程才是Mathematica的最大优势,因为博客不能直接放Mathematica的代码,那么就只好截图如下了
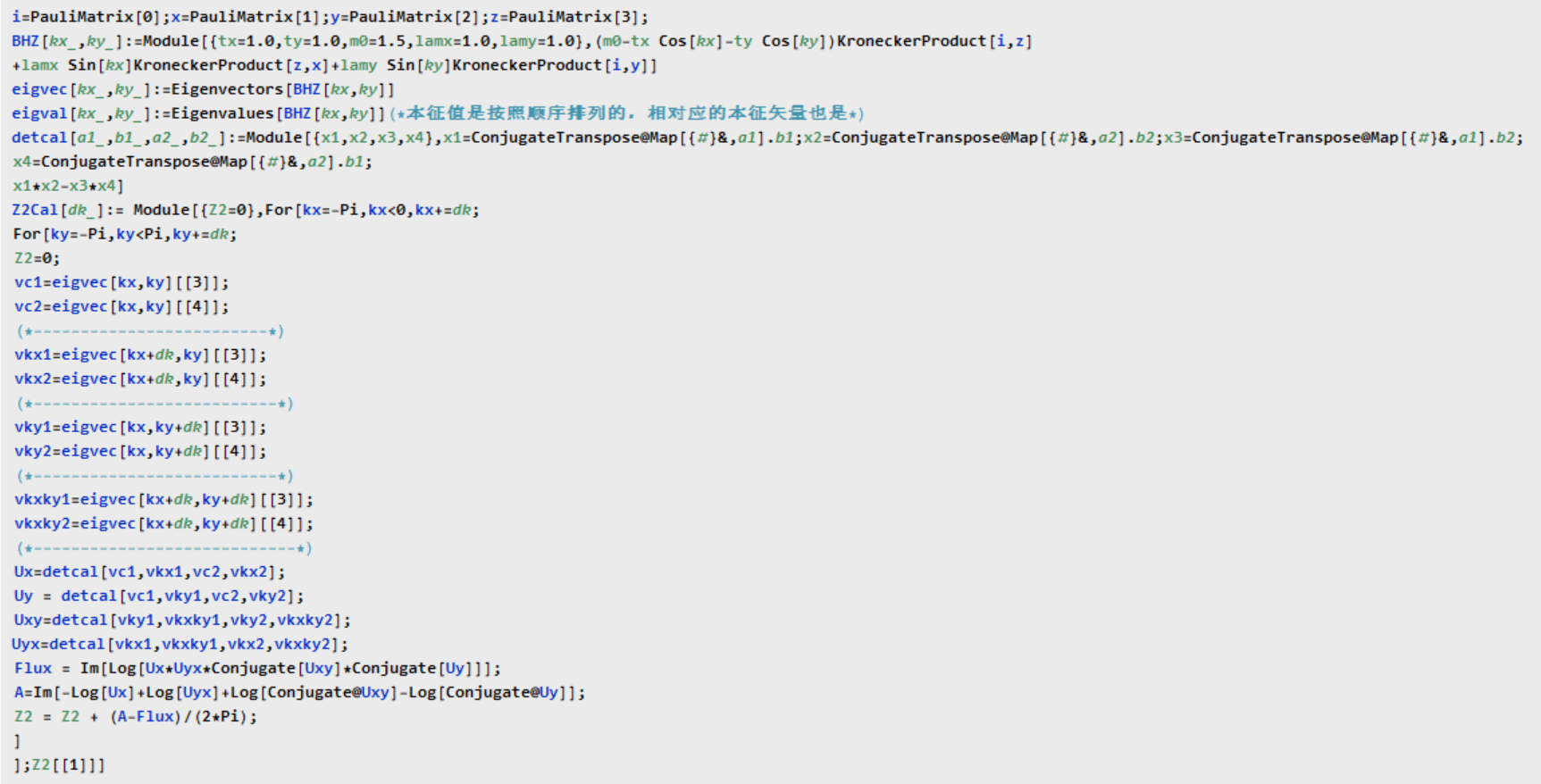
至于Mathematica的代码,可以点击这里下载.
在利用mma计算的时候,发现一些奇怪的事情,我如果用11.2的版本,那么计算得到的结果是稳定的,也是正确的,而当我使用12.0的时候,计算得到的结果在间隔或者k点数目取不同值的时候,有时候会得到错误的结果,我只能将这个问题归结的软件自身的问题上,毕竟我在利用其它语言计算的时候,并没有遇到太多这方面的问题.
小疑问
在计算的时候,我曾把$dk=0.1$,这时候的结果是错误的,如果将这个间隔调小之后,就可以得到正确的结果。而我利用这里的python代码进行计算的时候,相同的间隔下面仍然得到正确的结果。我对比了python和julia计算得到的本征值和本征矢量,发现本征值的计算两个不同语言的结果是相同的,但是本征矢量则是不同的。但这个应该只是小问题,应该是可以忽略这个问题的。而且利用julia来计算的话,在速度上还是很有优势的。
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
