平时在计算时会用到python和julia,利用anaconda中的jupyter可以在浏览器中很方便的同时使用多种语言,在这里整理一下Anaconda的安装以及jupyter的使用.同时把一些平时计算用的最基本的东西也都整理到一起,算是对新手的一个指引,里面的内容不是很详细,我只是想介绍一下自己平时用到的软件还有编程语言的最基本的一些操作.
软件下载
安装过程
1)在“Select Installation Type”界面的“Install for”中选择“All Users(requires admin privileges)”单选按钮
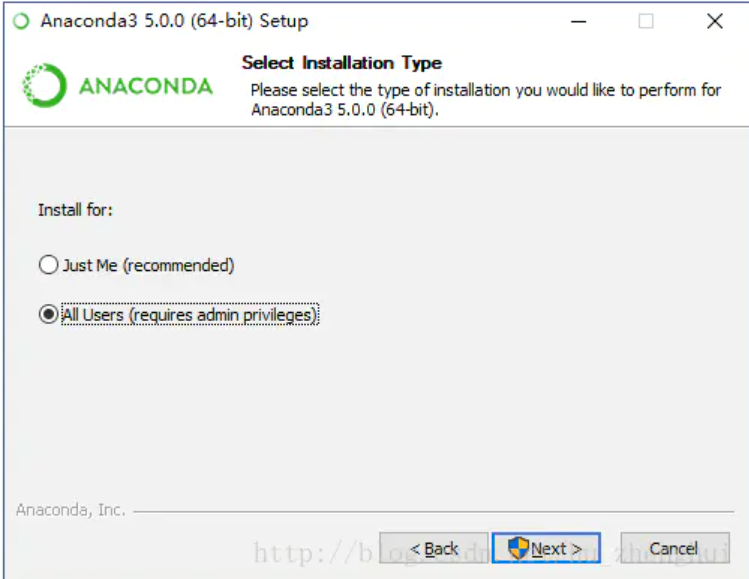
2)在“Choose Install Location”界面中查看“Destination Folder”,可能为C:\ProgramData\Anaconda3,注意检查该路径不能包含非英文字符
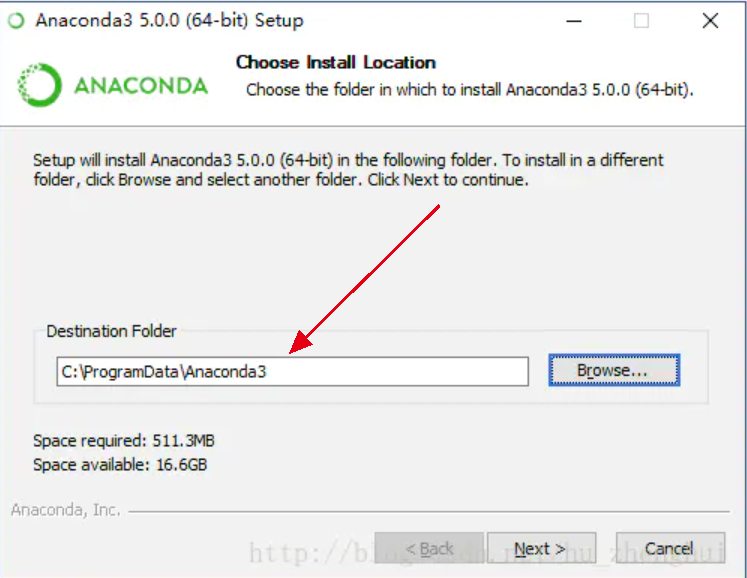
3)在“Advanced Installation Options”界面中选中“Register Anaconda as my default Python 3.6”复选框。
!png
建议这里不要选则将Anaconda增加到系统的环境变量中,增加太多会导致系统上的环境变量较为混乱.如果单独出来,后面对于Anaconda的包管理来说,也是较为简洁的,可以通过它自带的命令行来进行包管理.
4)安装完成后,开始==>所有程序中,出现文件夹anaconda3(64-bit)
Anaconda包管理
- 1.包更新升级
conda upgrade --all - 2.包安装 ```python conda install numpy scipy pandas
conda install numpy=1.10 安装指定版本的包
- 3.包移除
```python
conda remove package_name
Jupyter使用
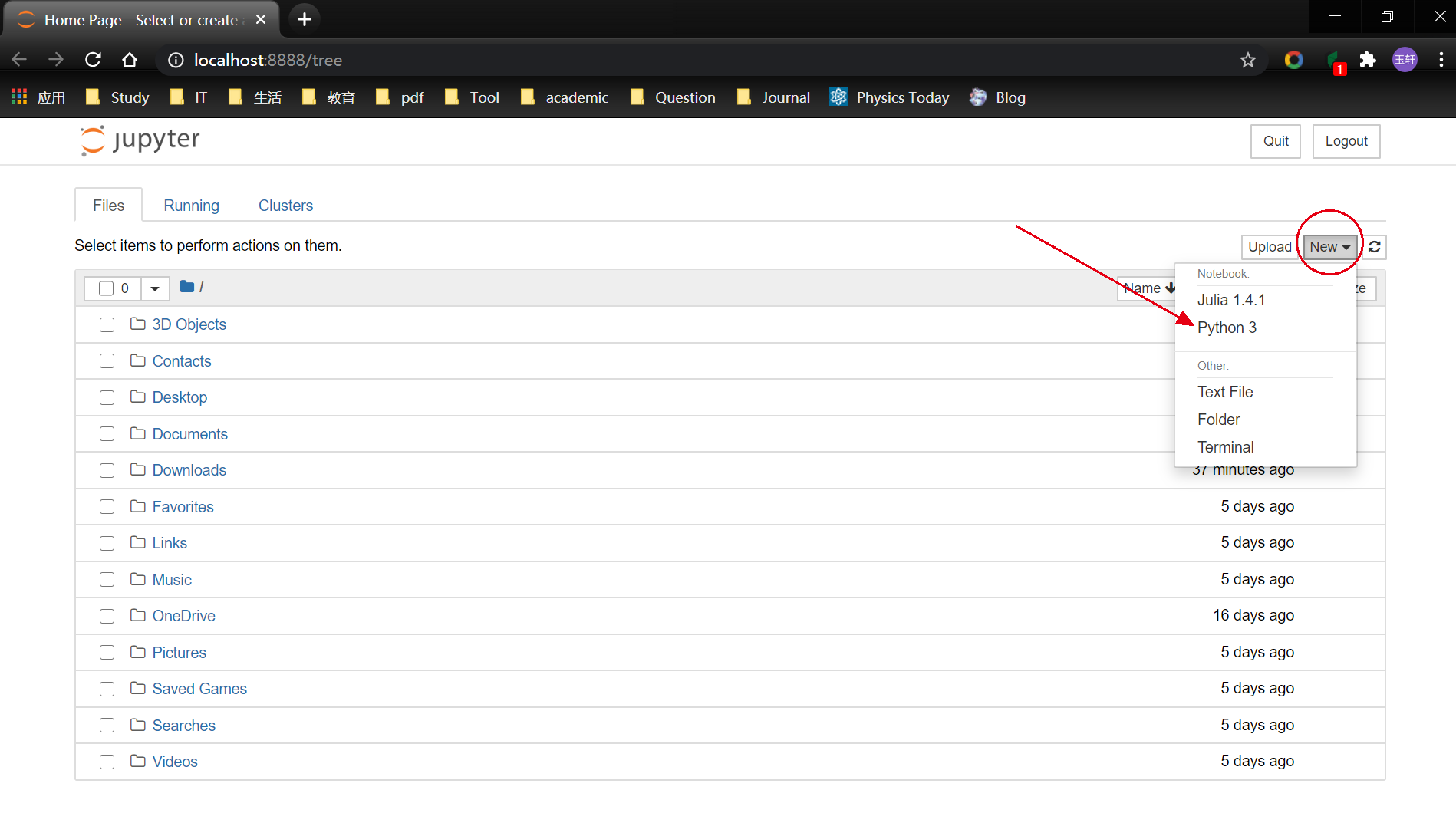
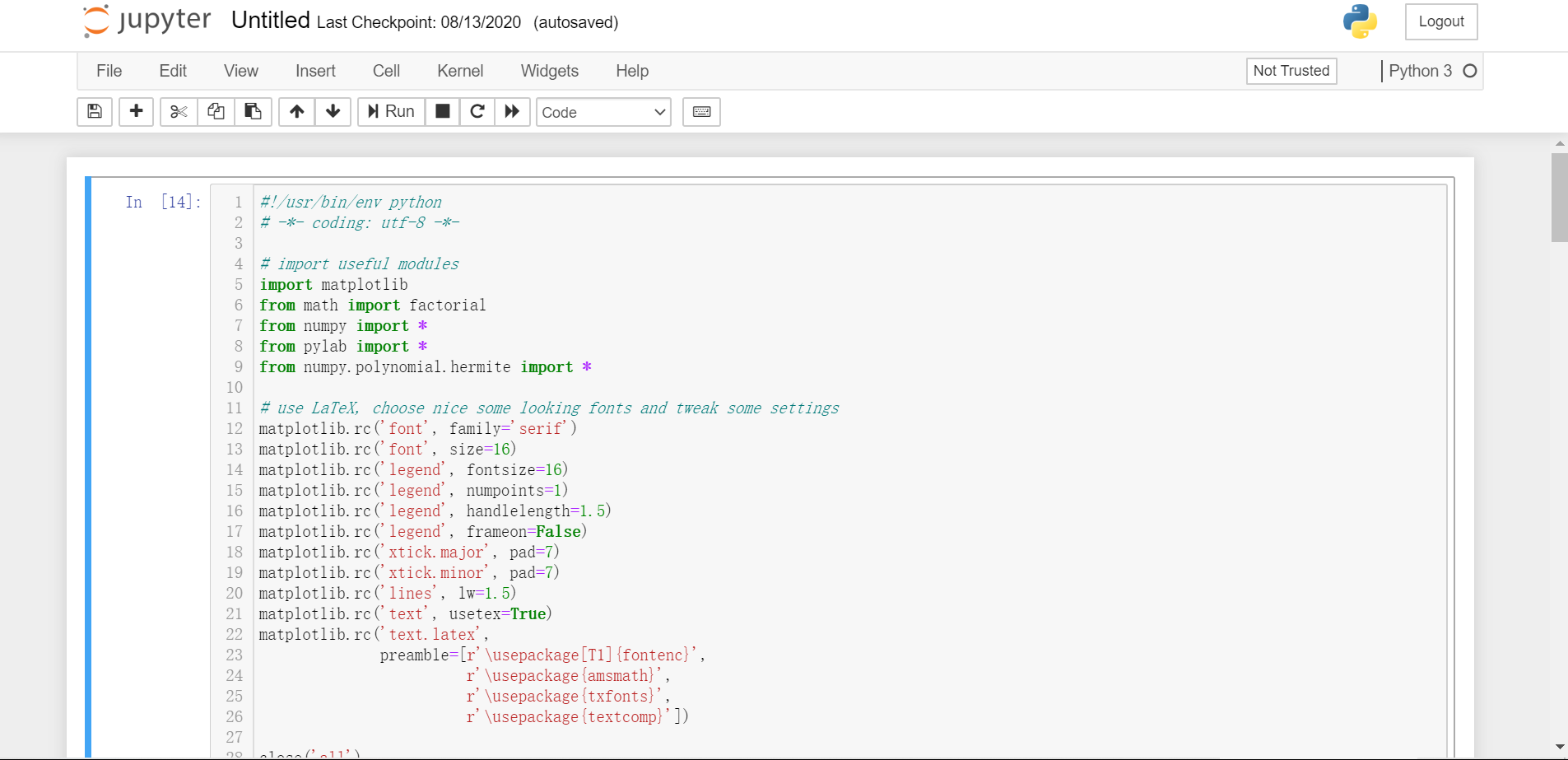
VsCode使用
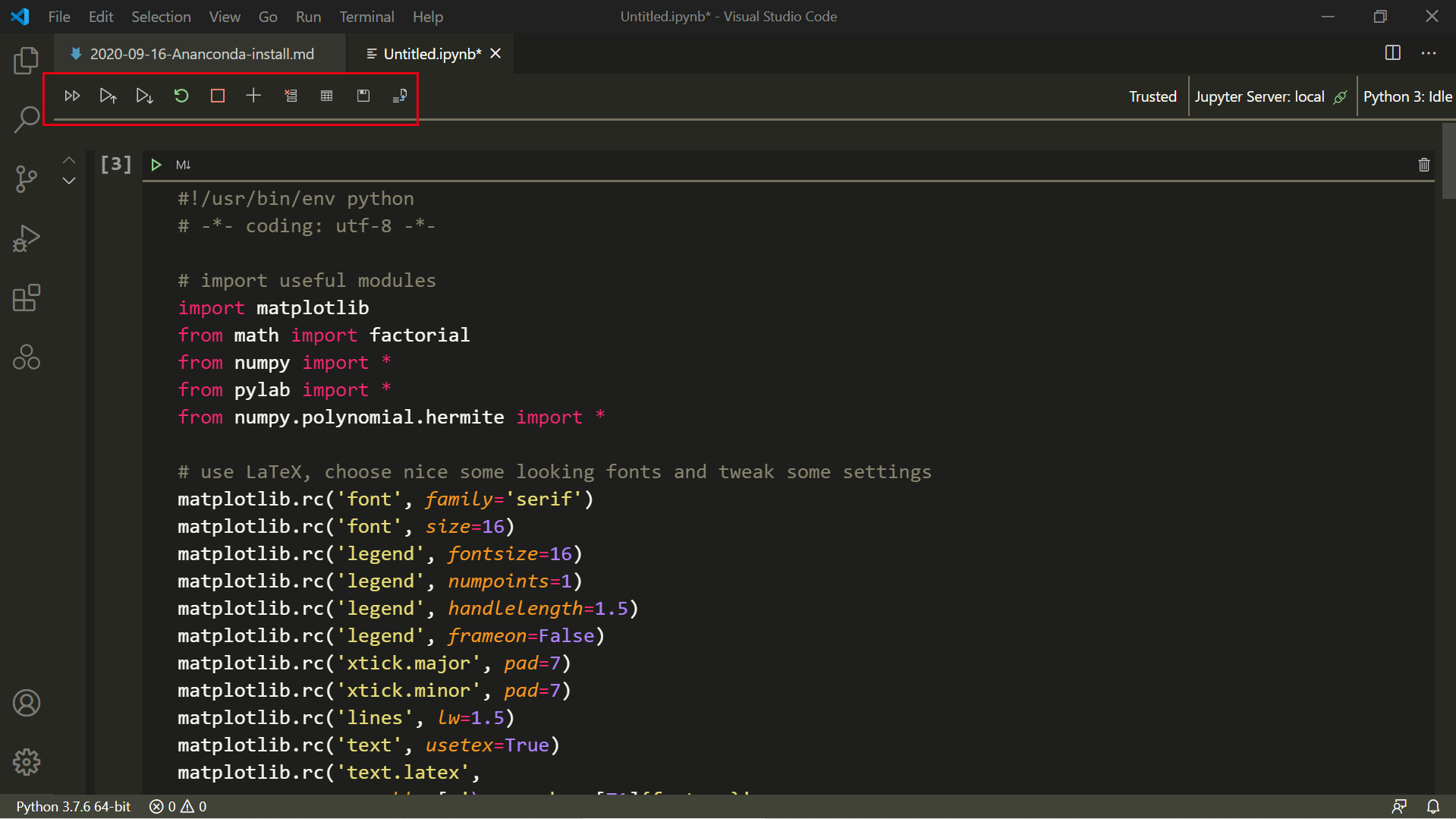
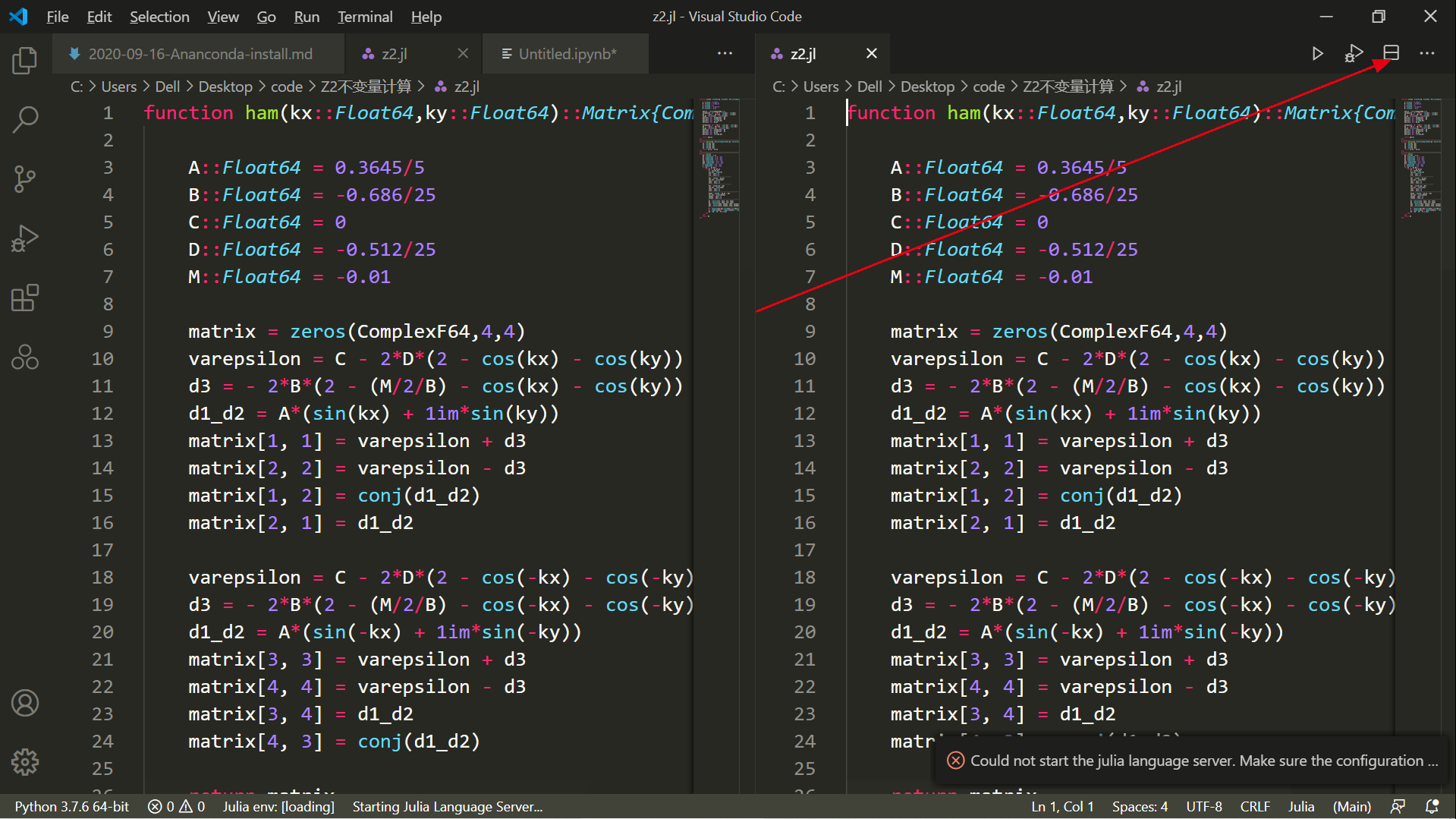
Plotly
Installation
pip install plotly==4.10.0
conda install -c plotly plotly=4.10.0
Jupyter Notebook Support
conda install "notebook>=5.3" "ipywidgets>=7.2"
plot
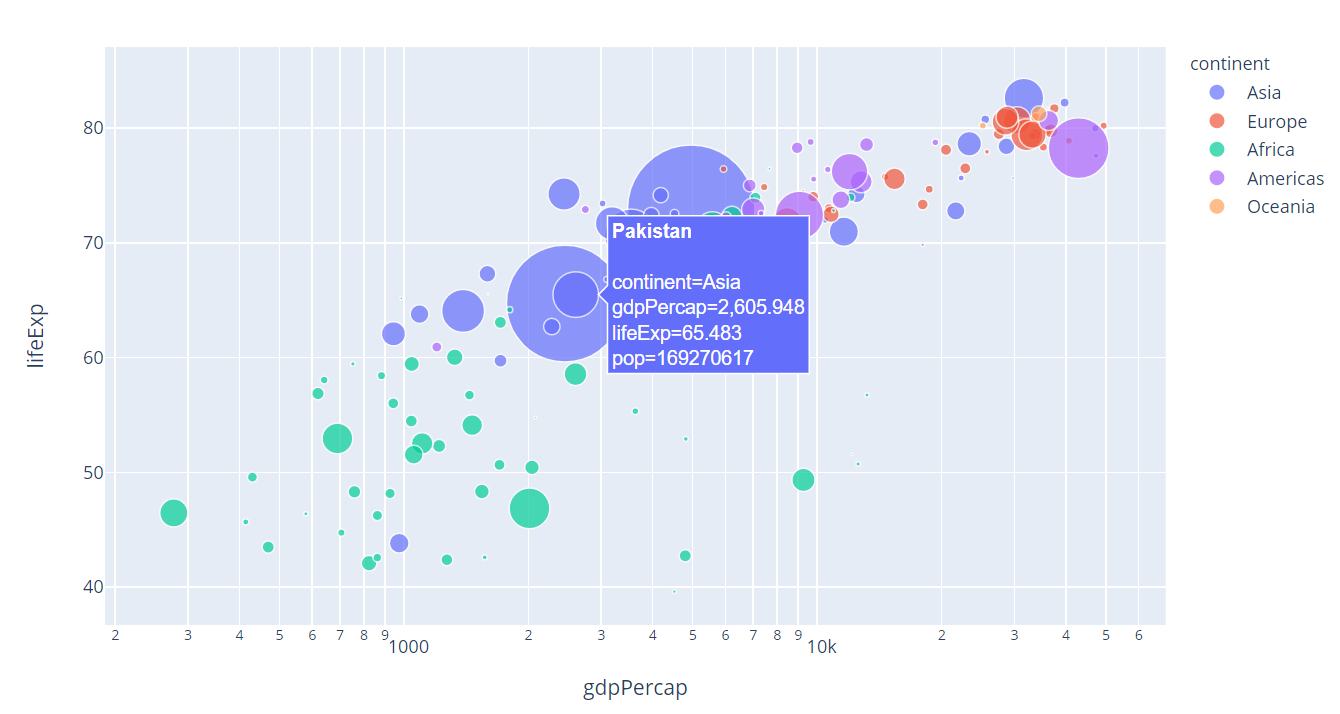
import plotly.graph_objects as go
# Valid color strings are CSS colors, rgb or hex strings
colorscale = [[0, 'gold'], [0.5, 'mediumturquoise'], [1, 'lightsalmon']]
fig = go.Figure(data =
go.Contour(
z=[[10, 10.625, 12.5, 15.625, 20],
[5.625, 6.25, 8.125, 11.25, 15.625],
[2.5, 3.125, 5., 8.125, 12.5],
[0.625, 1.25, 3.125, 6.25, 10.625],
[0, 0.625, 2.5, 5.625, 10]],
colorscale=colorscale)
)
fig.show()
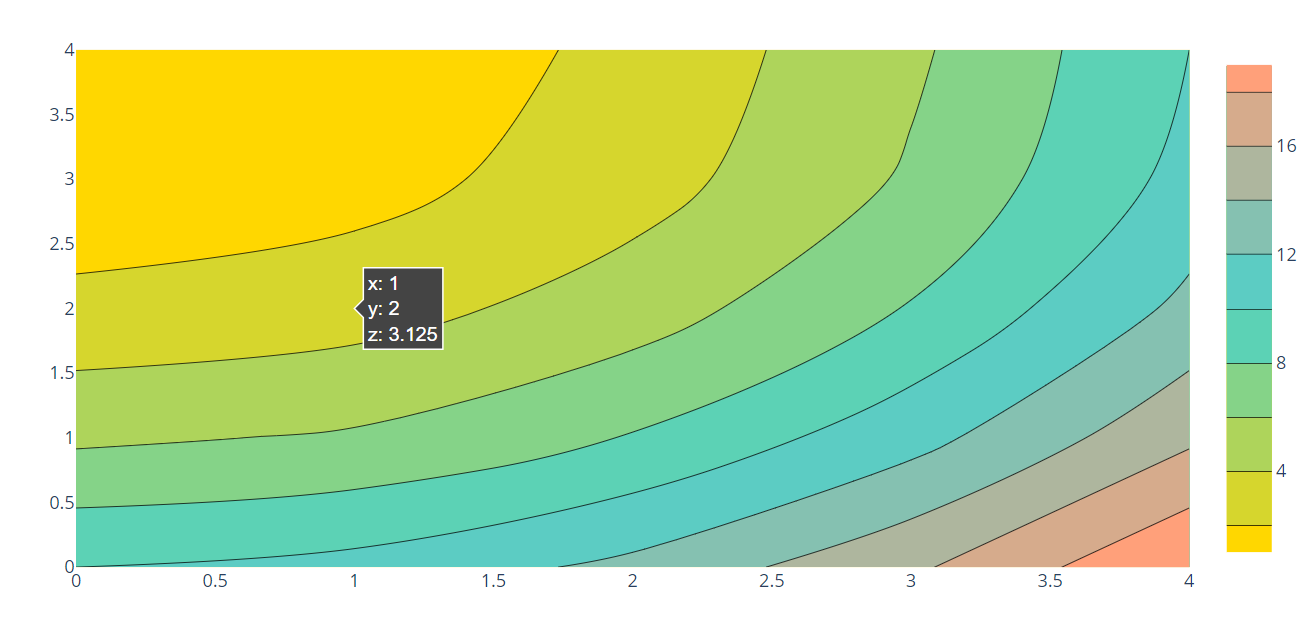
体积图
import plotly.graph_objects as go
import numpy as np
X, Y, Z = np.mgrid[-1:1:30j, -1:1:30j, -1:1:30j]
values = np.sin(np.pi*X) * np.cos(np.pi*Z) * np.sin(np.pi*Y)
fig = go.Figure(data=go.Volume(
x=X.flatten(),
y=Y.flatten(),
z=Z.flatten(),
value=values.flatten(),
isomin=-0.1,
isomax=0.8,
opacity=0.1, # needs to be small to see through all surfaces
surface_count=21, # needs to be a large number for good volume rendering
))
fig.show()
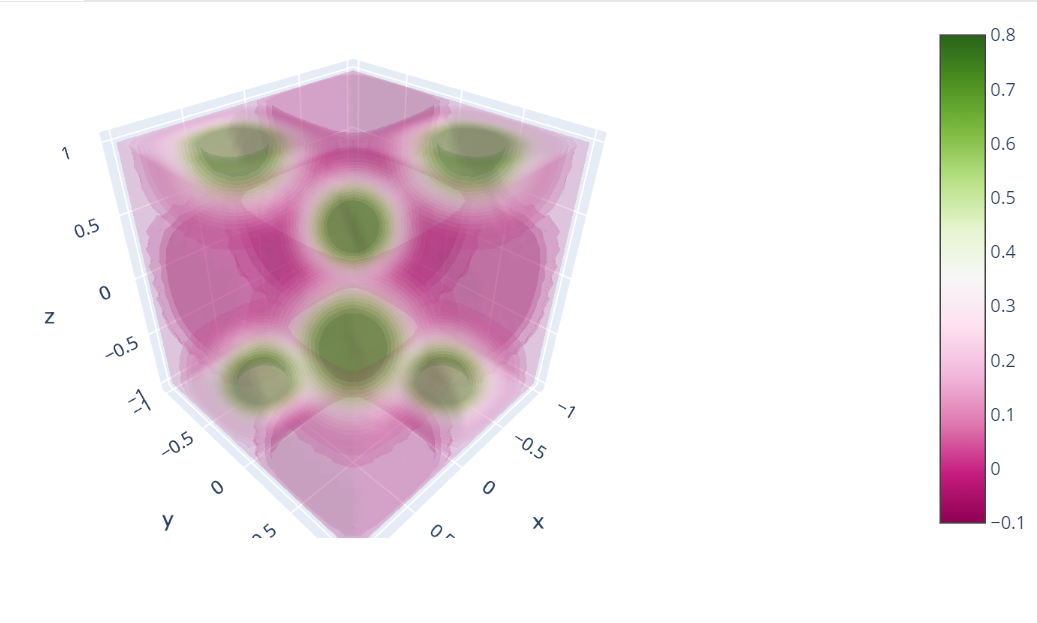
import plotly.graph_objects as go
import numpy as np
X, Y, Z = np.mgrid[-1:1:30j, -1:1:30j, -1:1:30j]
values = np.sin(np.pi*X) * np.cos(np.pi*Z) * np.sin(np.pi*Y)
fig = go.Figure(data=go.Volume(
x=X.flatten(),
y=Y.flatten(),
z=Z.flatten(),
value=values.flatten(),
isomin=-0.5,
isomax=0.5,
opacity=0.1, # max opacity
opacityscale=[[-0.5, 1], [-0.2, 0], [0.2, 0], [0.5, 1]],
surface_count=21,
colorscale='RdBu'
))
fig.show()
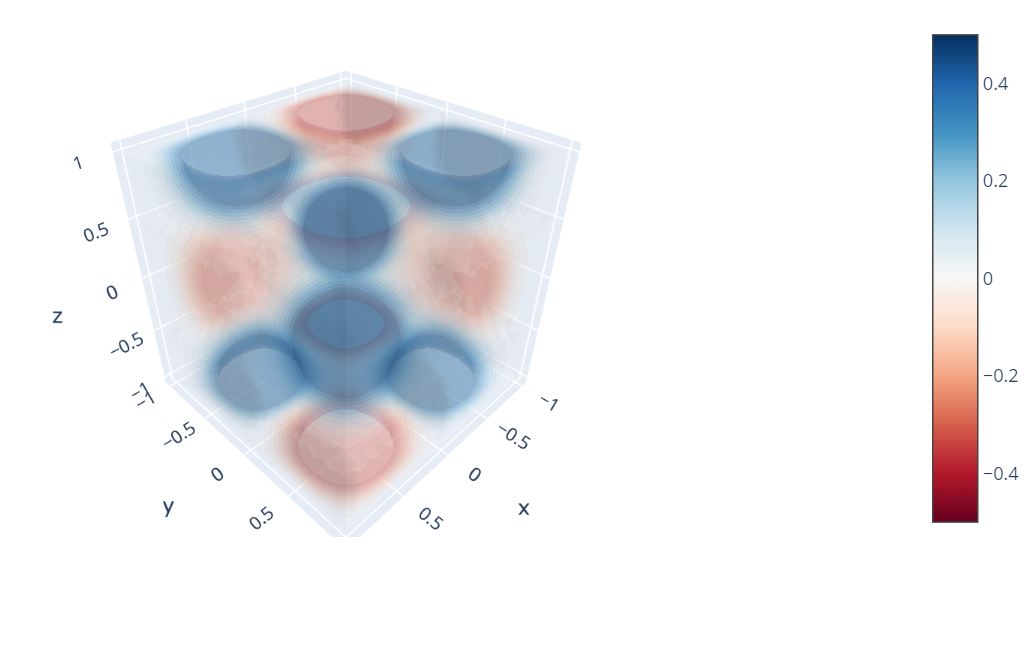
服务器程序编译执行
Linux基本命令
ls or ls -al 显示当前文件夹中的所有文件
pwd 打印当前路径
mkdir f1 创建一个名为f1的文件夹
clear 清除中断显示的所有内容
cd /home 切换到根目录下的home文件夹,这个命令可以配合pwd使用,可以自己决定切换到哪一个目录,只要路径名称是正确的,其你是拥有文件的访问权限
vim te.f90 在终端打开te.f90文件
gedit te.f90 以图形界面的方式打开te.f90文件
diff f1 f2 比较两个文件之间的差异
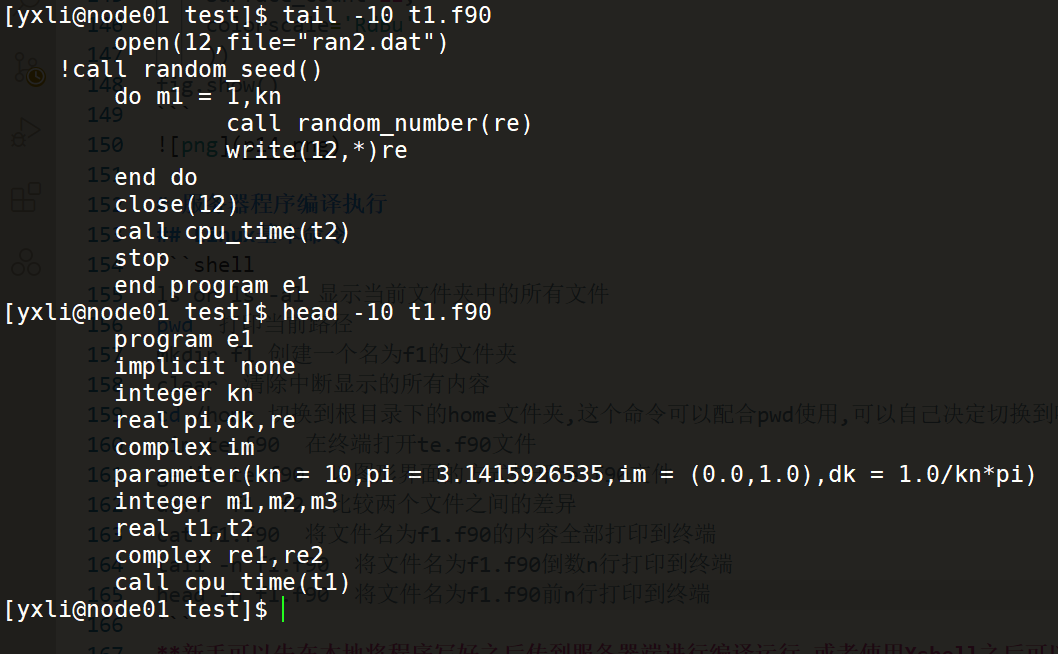
cat f1.f90 将文件名为f1.f90的内容全部打印到终端
tail -n f1.f90 将文件名为f1.f90倒数n行打印到终端
head -n f1.f90 将文件名为f1.f90前n行打印到终端
新手可以先在本地将程序写好之后传到服务器端进行编译运行,或者使用Xshell之后可以直接使用gedit在服务器端利用图形界面对代码进行直接修改,vim使用需要一定的学习.
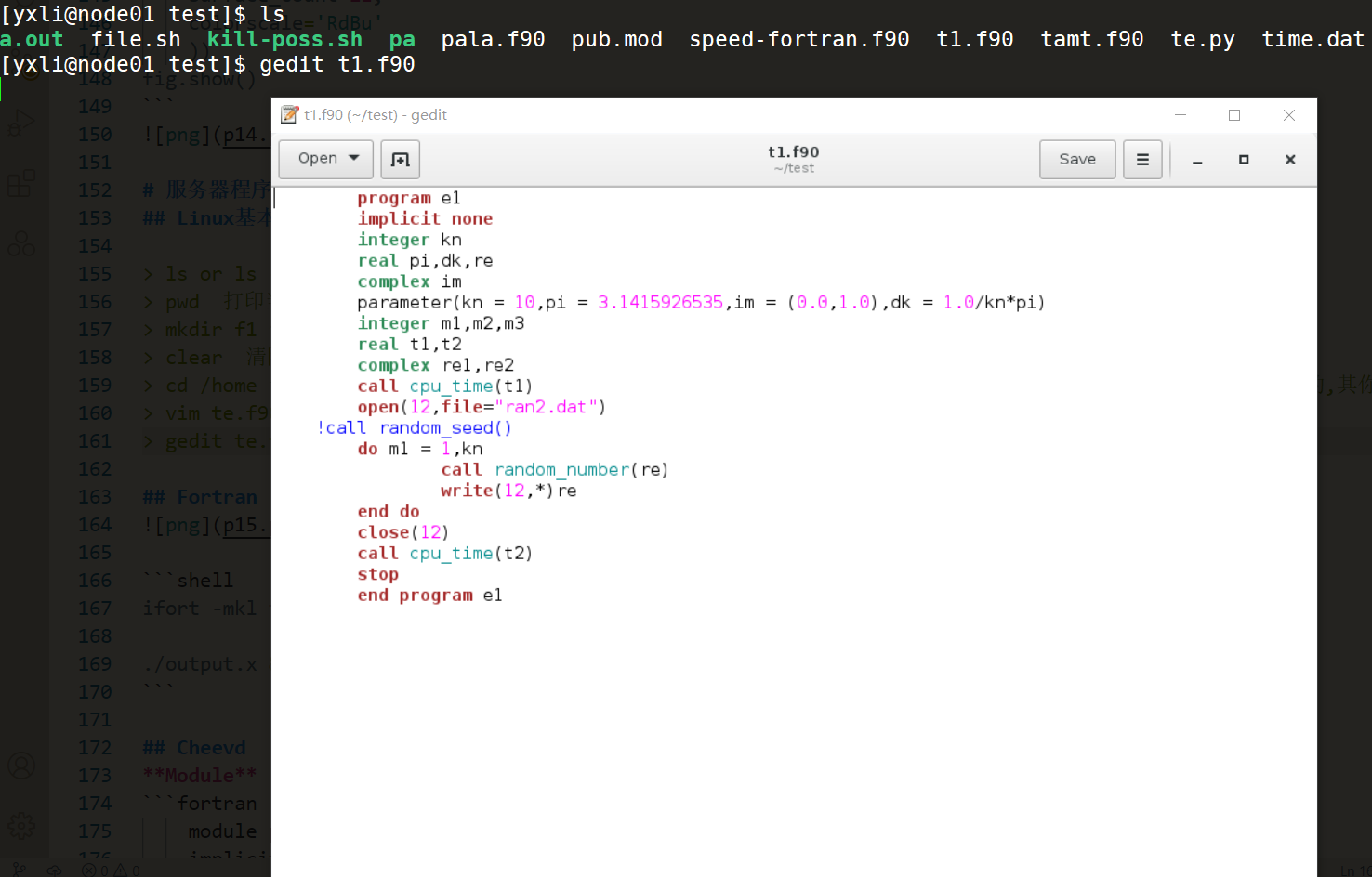
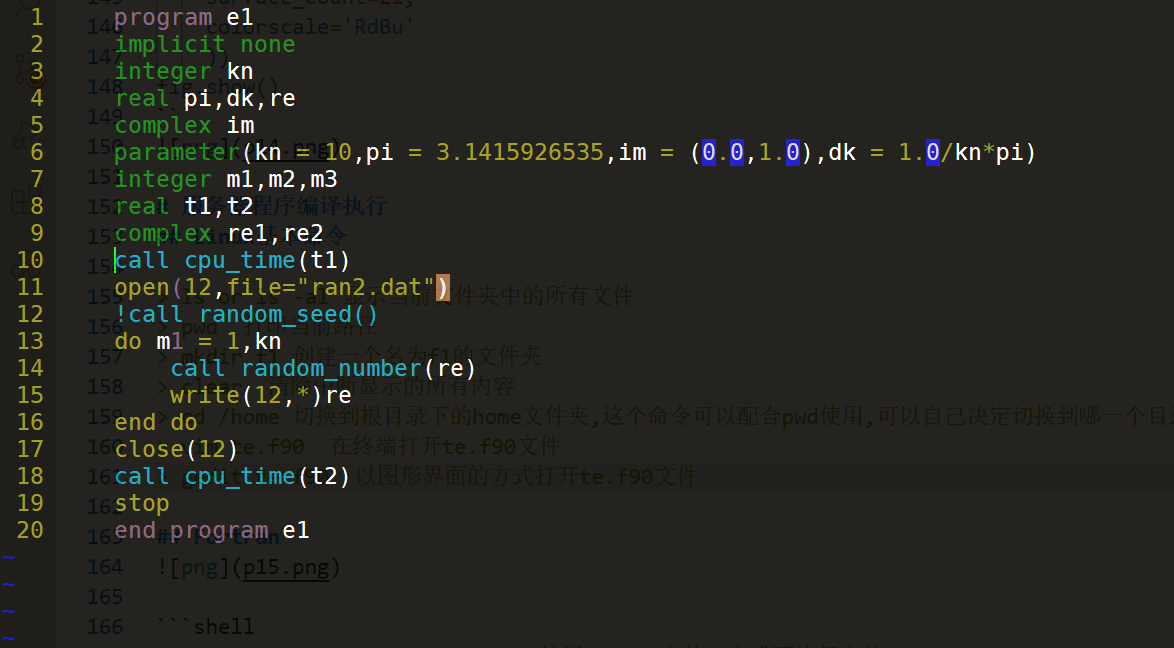
Fortran
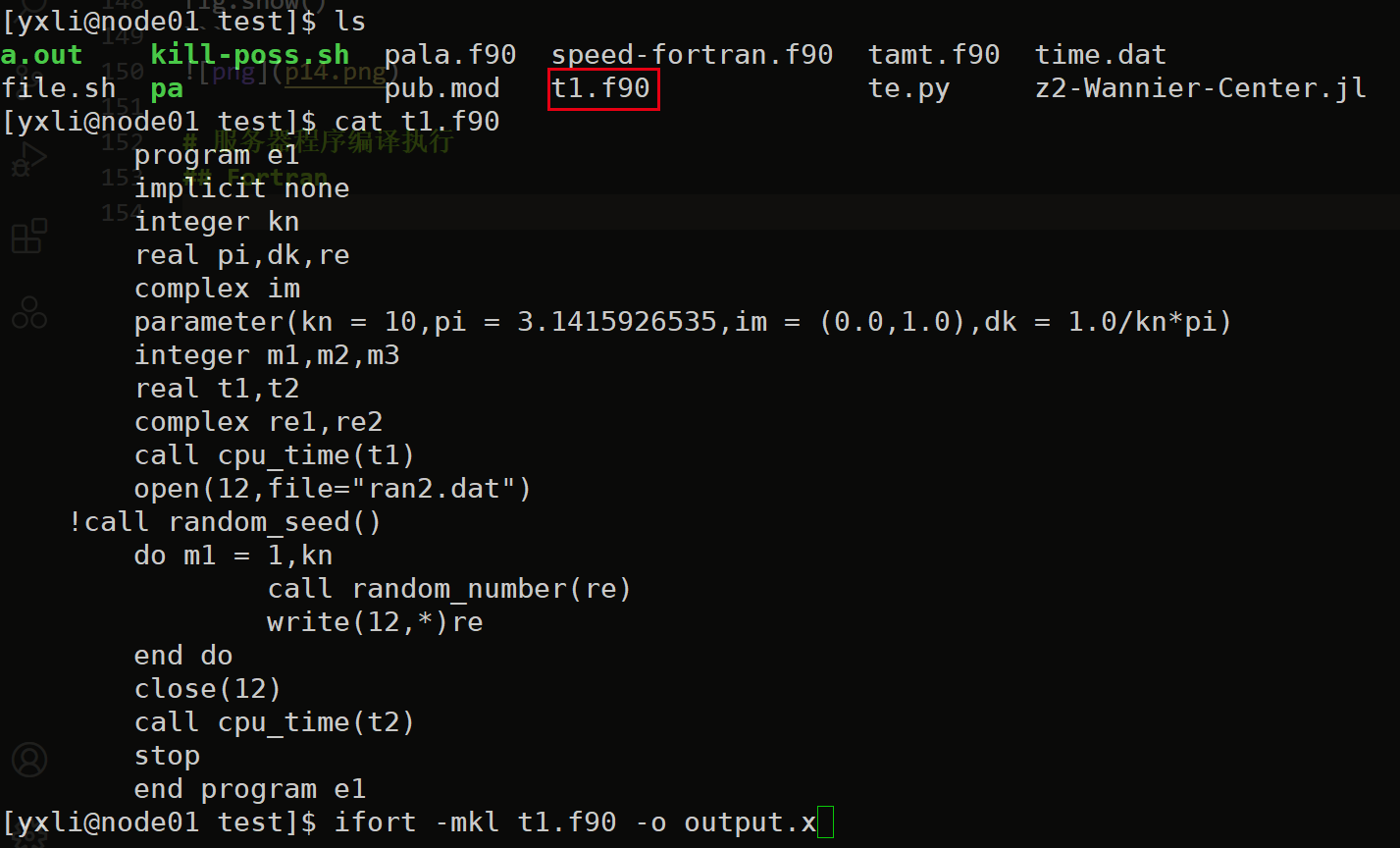
ifort -mkl t1.f90 -o output.x 编译t1.f90文件,生成可执行文件output.x
./output.x & 执行output.x 并放到后台执行
如果矩阵维数较大,需要加入额外的编译选项
ifort -mkl -mcmodel=large t1.f90 -o output.x !-mcmodel=large 是为了让编译器可以接受维数更大的矩阵
ifort -mkl -O3 t1.f90 -o output.x 加入-O3选项可以让编译器对一些内容进行默认操作,文档说这是一种相对激进的编译选项,可以有一定速度提升
Cheevd
Module
module pub
implicit none
integer xn,yn,ne
parameter(xn = 30,yn = 30,ne = 1000)
integer,parameter::N = xn*yn*8
integer::lda = N
integer,parameter::lwmax=2*N+N**2
real,allocatable::w(:)
complex*8,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork ! at least 2*N+N**2
integer lrwork ! at least 1 + 5*N +2*N**2
integer liwork ! at least 3 +5*N
integer info
end module pub
对角化函数调用
subroutine eigsol()
use pub
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file="mes.txt",status="unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
open(12,file="eigval.dat",status="unknown")
do m = 1,N
write(12,*)m,w(m)
end do
close(12)
return
end subroutine eigsol
程序示例
! Author:YuXuanLi
! E-Mail:yxli406@gmail.com
! Article:Majorana Corner Modes in a High-Temperature Platform
! Doi:10.1103/PhysRevLett.121.096803
!==========================================
module param
implicit none
integer xn,yn,nkx,nky,ne,nkxy
parameter(nkx=50,nky=50,ne=1000)
integer,parameter::N = 4
complex,parameter::im = (0.,1.) !Imagine unit
real,parameter::pi = 3.14159265358979
complex Ham(N,N) ! Hamiltonian Matrix
real mu ! Chemical Potential
real tx,ty ! hopping term energy
real ax,ay ! copule energy
real m0 !Driac mass
real kx,ky
! LAPACK PACKAGE PARAM
integer::lda = N
integer,parameter::lwmax = 2*N+N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork ! at least 2*N+N**2
integer lrwork ! at least 1 + 5*N +2*N**2
integer liwork ! at least 3 +5*N
integer info
end module param
!========== PROGRAM START ==========================
program sol
use param
integer m,l ! loop variales
!================ Physics memory allocate =================
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
! paramater set value
m0 = 1.5 ! effective mass
tx = 1.0 ! hopping energy in x direction
ty = 1.0 ! hopping energy in y direction
mu = 0.2 ! chemical potential
ax = 1.0 ! couple energy in x direction
ay = 1.0 ! couple energy in y direction
call band()
stop
end program
!===========================================================
subroutine matrix_set()
use param
Ham = 0
!----------------------------------------------
Ham(1,1) = m0 - tx*cos(kx) - ty*cos(ky) + mu
Ham(2,2) = -(m0 - tx*cos(kx) - ty*cos(ky)) + mu
Ham(3,3) = m0 - tx*cos(kx) - ty*cos(ky) + mu
Ham(4,4) = -(m0 - tx*cos(kx) - ty*cos(ky)) + mu
!-----------------------------------------------
Ham(1,2) = ax*sin(kx) - im*ay*sin(ky)
Ham(2,1) = ax*sin(kx) + im*ay*sin(ky)
Ham(3,4) = -ax*sin(kx) - im*ay*sin(ky)
Ham(4,3) = -ax*sin(kx) + im*ay*sin(ky)
!--------------------------------------------------
call ishermitian()
end subroutine matrix_set
!============================================================
subroutine band()
! Evaluate the density of state in (x,y) position
use param
integer m,l,k,i! circle variable
open(12,file="tiband.dat")
! (0,0)------>(pi,0)
do k = 0,nky
kx = pi*k/nkx ! discrete wavevector in x direction
!kx = 0
ky = 0 ! discrete wavevector in y direction
! 不同的kx和ky重新进行哈密顿量矩阵的构造和求解
call matrix_set() ! 新的kx和ky下重新填充矩阵,并求解对应本征值
call eigSol()
write(12,"(6f9.5)")kx,ky,(w(i),i=1,N)
end do
! (pi,0)---->(pi,pi)
do k = 0,nkx
kx = pi
ky = pi*k/nkx ! discrete wavevector in y direction
! 不同的kx和ky重新进行哈密顿量矩阵的构造和求解
call matrix_set() ! 新的kx和ky下重新填充矩阵,并求解对应本征值
call eigSol()
write(12,"(6f9.5)")kx,ky,(w(i),i=1,N)
end do
! (pi,pi)---->(0,0)
do k = 0,nkx-1
kx = pi-pi*k/nkx ! discrete wavevector in x direction
ky = pi-pi*k/nky ! discrete wavevector in y direction
call matrix_set() ! 新的kx和ky下重新填充矩阵,并求解对应本征值
call eigSol()
write(12,"(6f9.5)")kx,ky,(w(i),i=1,N)
end do
close(12)
end subroutine band
!============================================================
subroutine ishermitian()
use param
integer i,j
integer ccc
ccc = 0
open(16,file = 'verify.dat')
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
ccc = ccc +1
write(16,*)i,j
write(16,*)Ham(i,j)
write(16,*)Ham(j,i)
end if
end do
end do
write(16,*)ccc
close(16)
return
end subroutine ishermitian
!================= Hermitain Matrices solve ==============
subroutine eigSol()
use param
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(101,file="mes.txt",status="unknown")
write(101,*)'The algorithm failed to compute eigenvalues.'
close(101)
end if
open(100,file="eigval.dat",status="unknown")
do m = 1,N
write(100,*)m,w(m)
end do
close(100)
return
end subroutine eigSol
Python
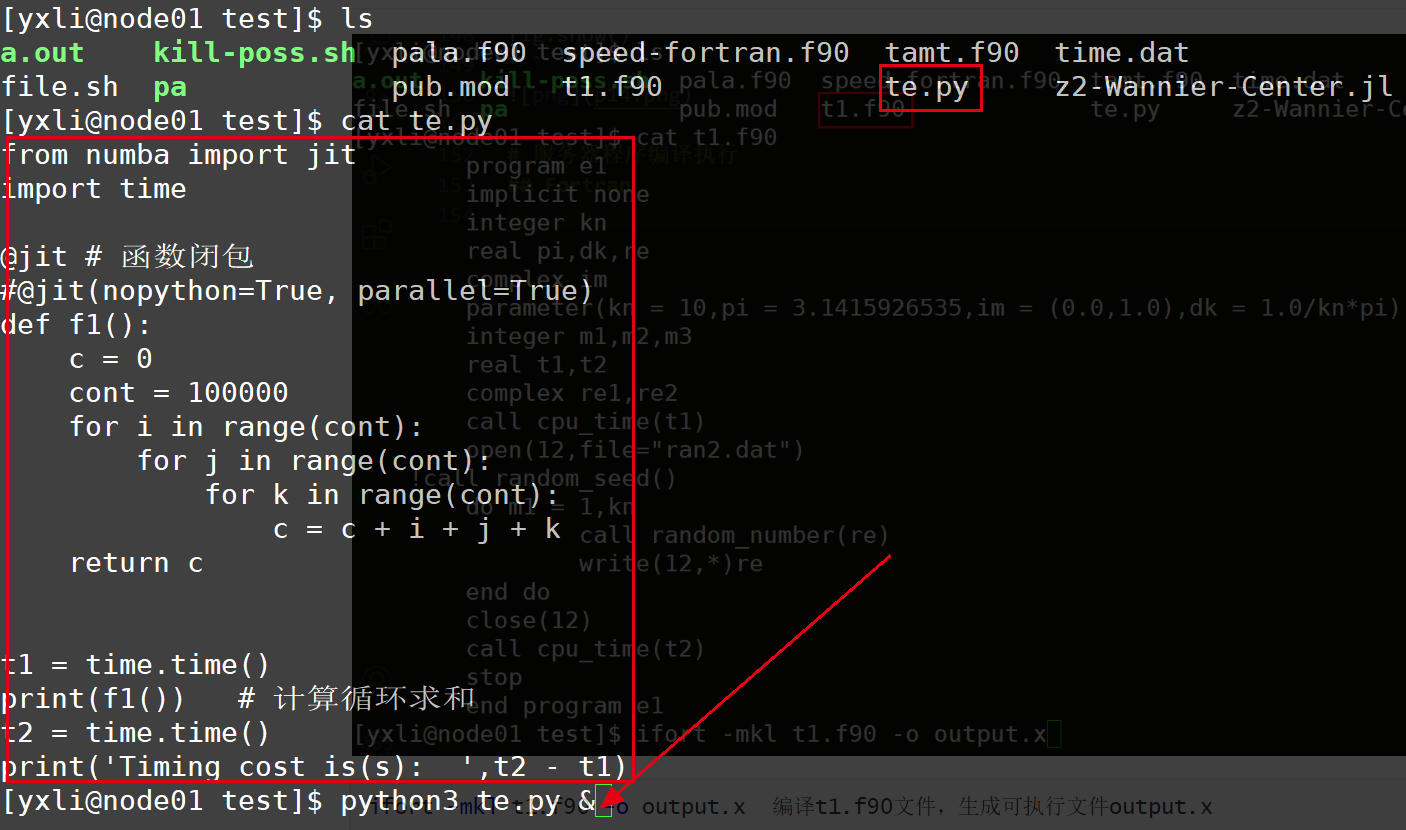
python3 te.py & 执行python程序,并放到后台执行(python不用编译)
julia的执行和python相同
Origin作图
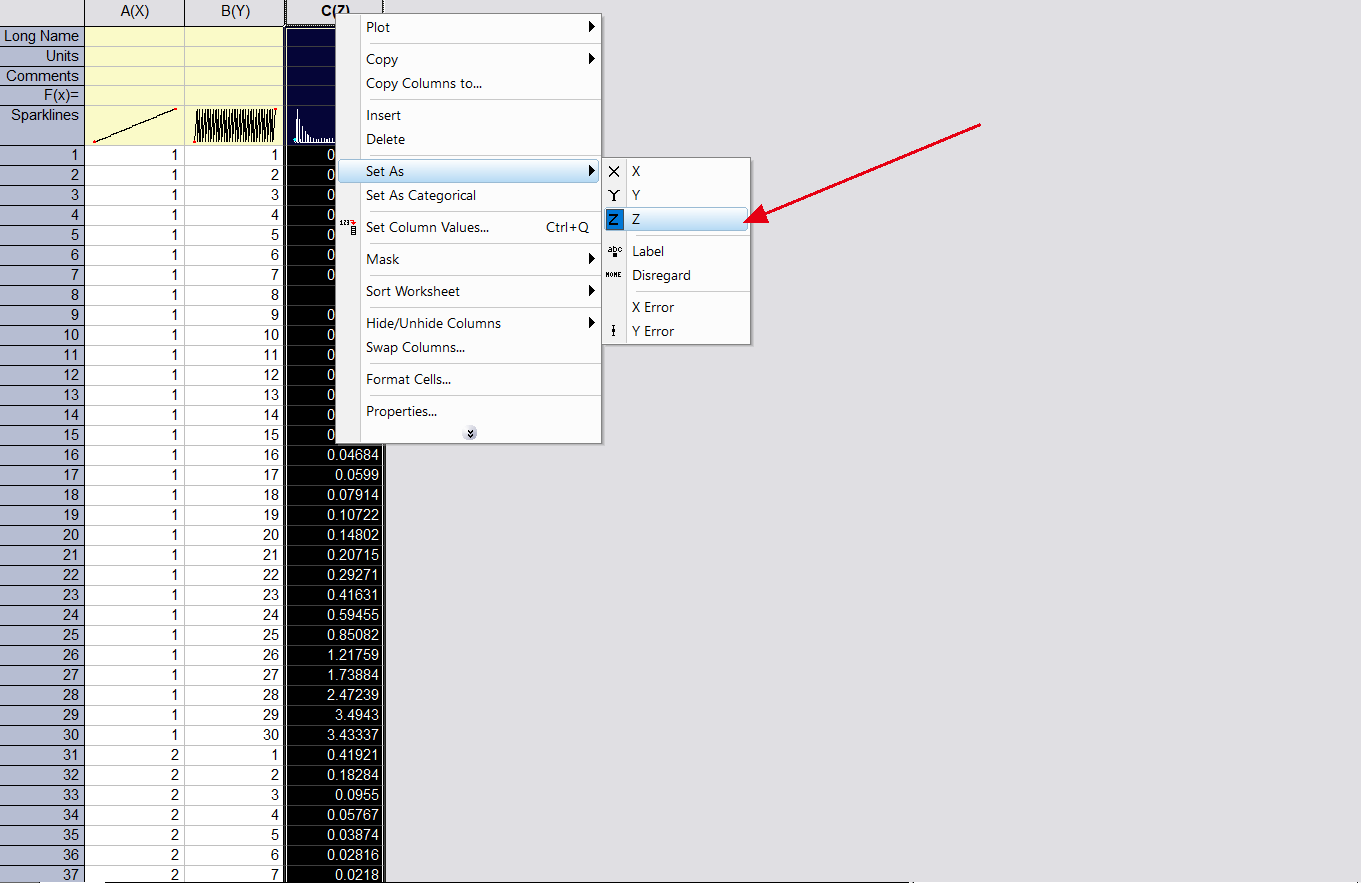
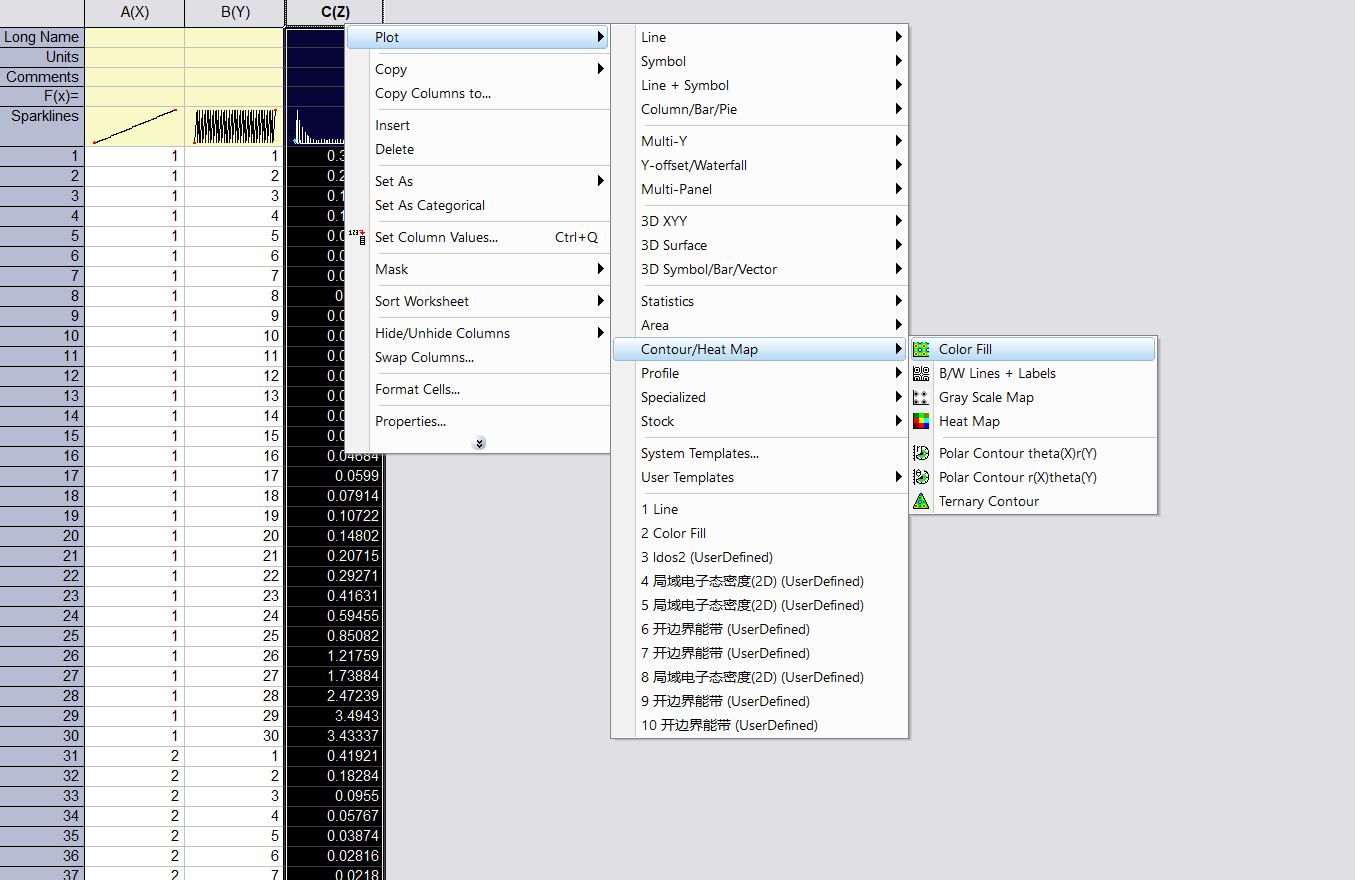
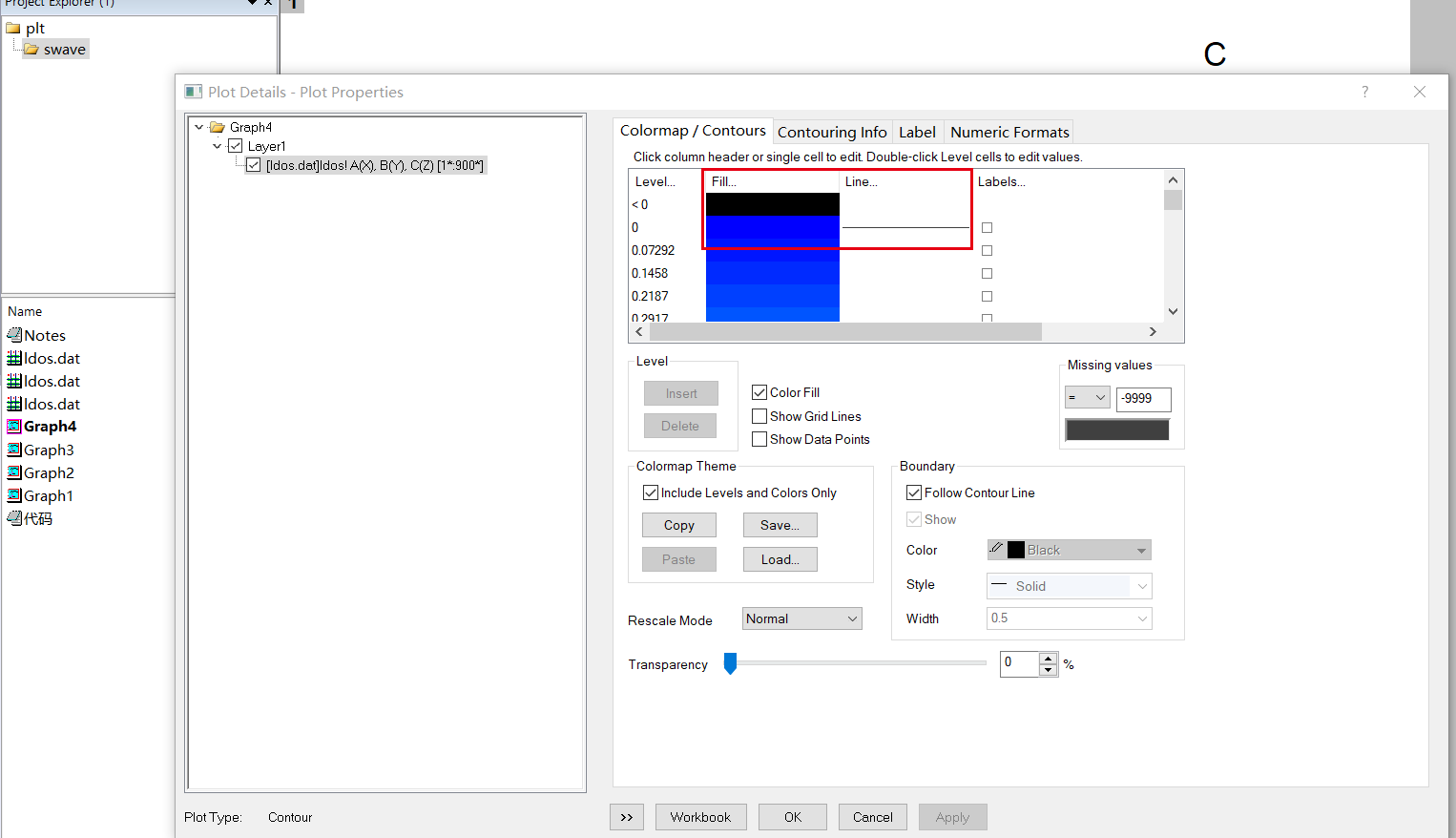
坐标轴样式调节
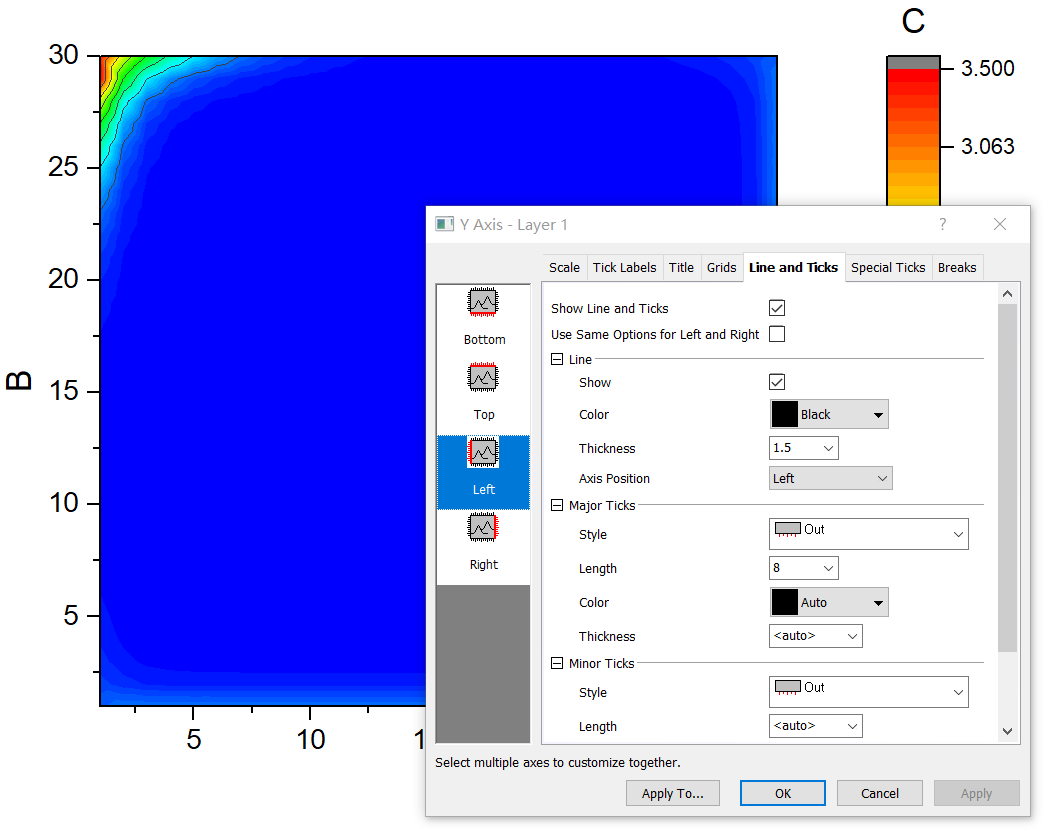
建立自己的作图模板
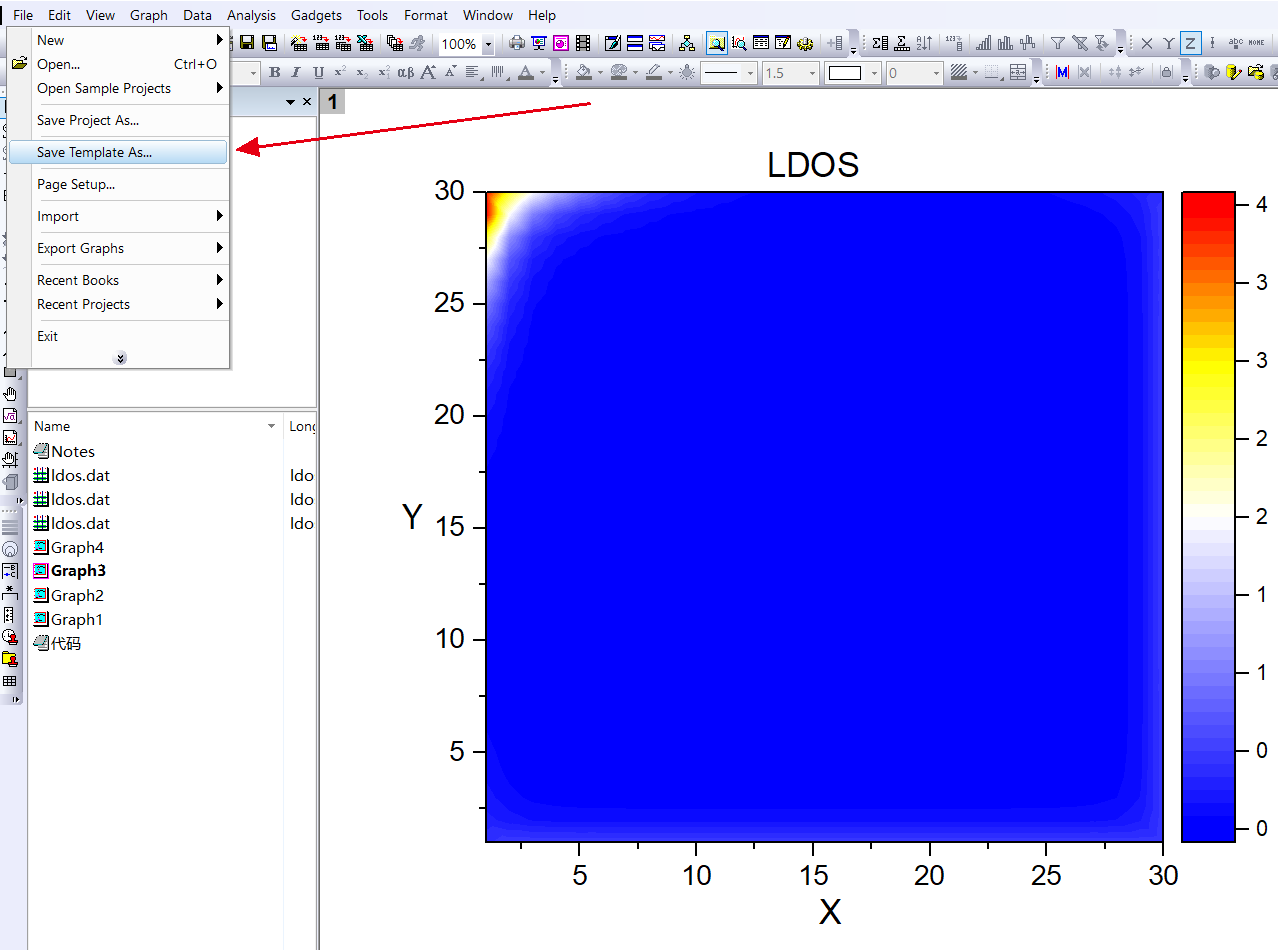
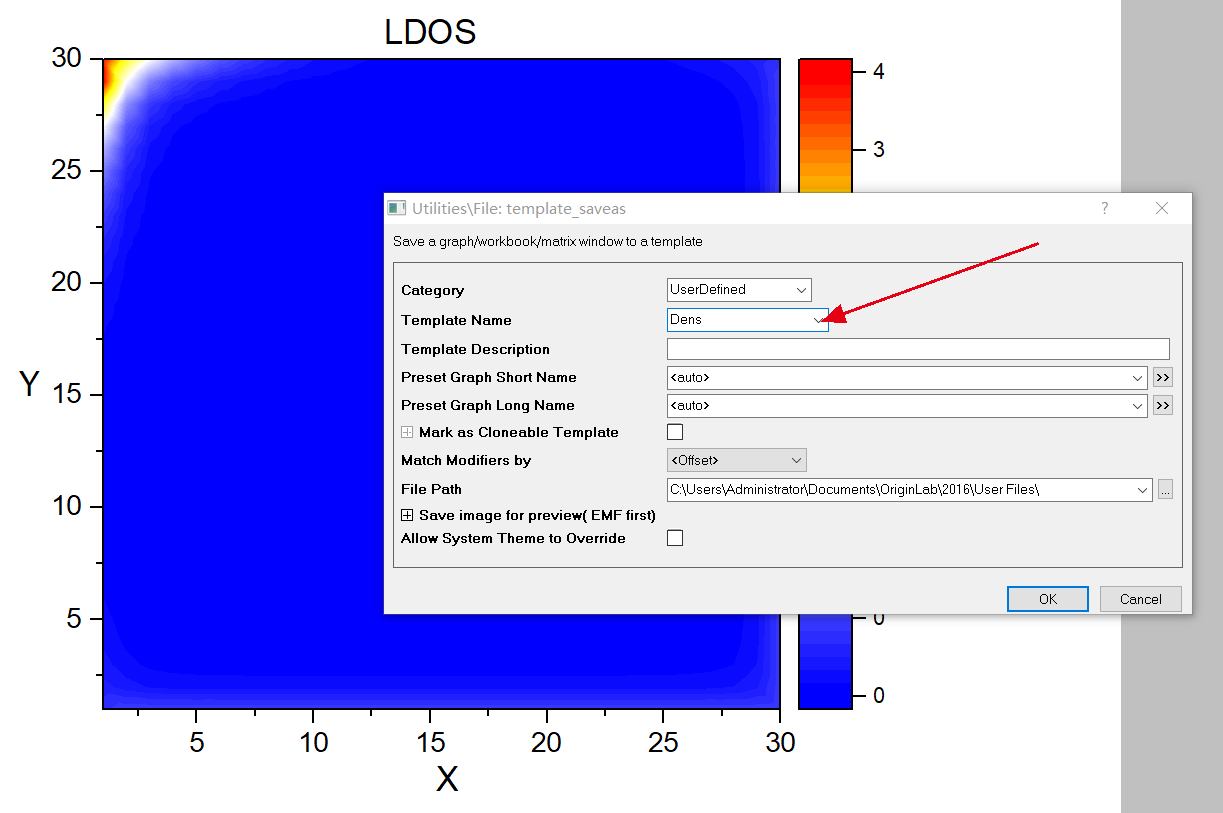
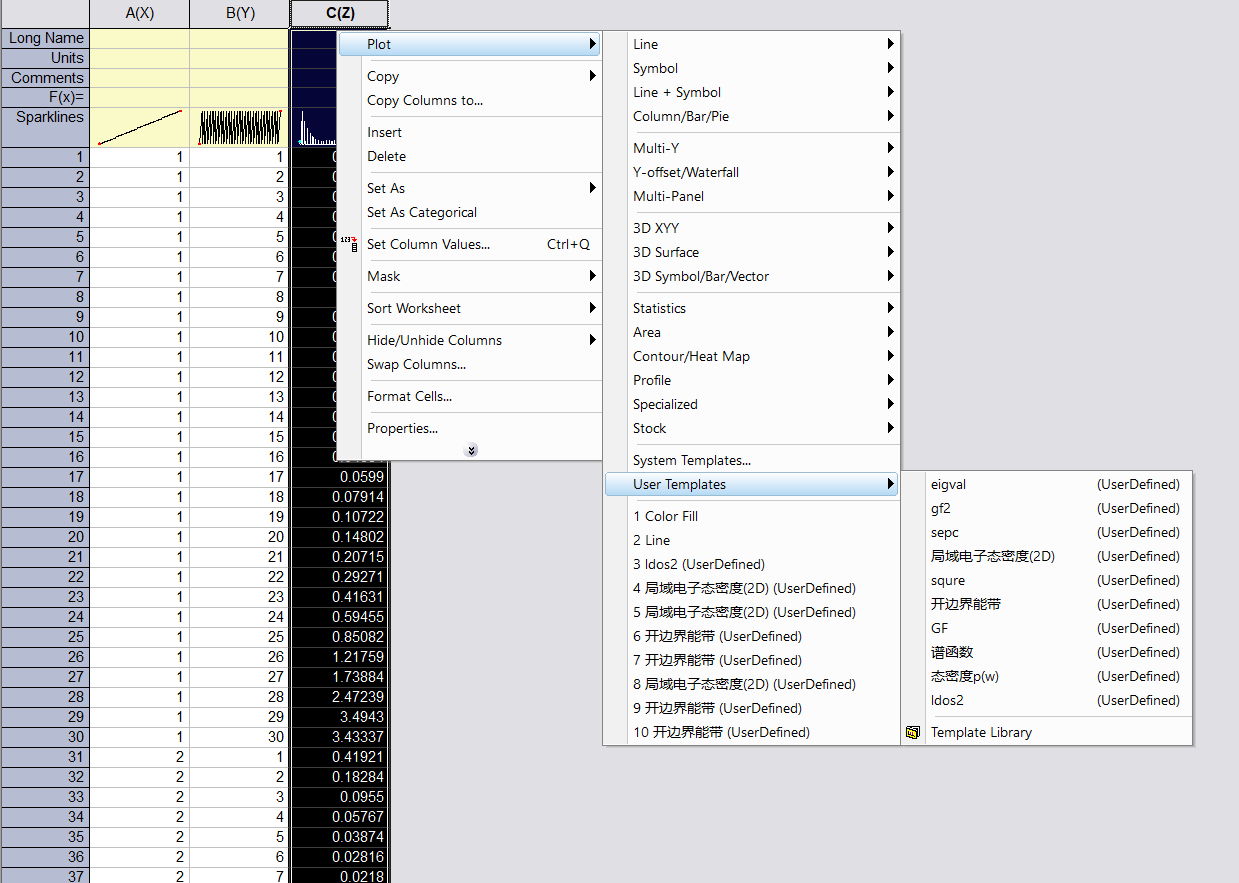
补充
- 批量编译执行Fortran程序
仅仅执行确定文件夹下的Fortran程序,再下一级目录中文件不会去执行
#!/bin/sh #============ get the file name =========== Folder="/home/yxli/te" #要批量编译哪个文件夹下面的Fortran for file_name in ${Folder}/*.f90 do temp_file=`basename $file_name .f90` ifort -mkl $file_name -o $temp_file.out ./$temp_file.out & # 编译成功之后自动运行 done rm *out # 删除编译后文件 - 批量执行文件夹中所有的Fortran程序(文件夹中可以包含文件夹) 递归搜寻文件夹下面所有的Fortran文件
#!/bin/bash
function getdir(){
for element in `ls $1`
do
dir_or_file=$1"/"$element
if [ -d $dir_or_file ]
then
getdir $dir_or_file
else # 下面的全是文件
if [ "${dir_or_file##*.}"x = "f90"x ]||[ "${dir_or_file##*.}"x = "f"x ];then # 筛选处特定后缀的文件
dir_name=`dirname $dir_or_file` # 读取目录
file_name=`basename $dir_or_file .f90` # 读取以f90结尾的文件名
out_file_name="$dir_name/$file_name" # 定义编号成功的文件名称
ifort -mkl $dir_or_file -o $out_file_name.out # 编译后文件名以out结尾
dir1=`dirname $out_file_name` # 读取编译成功文件的路径,只提取目录
cd $dir1 # 切换到具体的文件夹
./$file_name.out 1>mes 2>bad & # 执行该文件夹下面编译好的文件
# ./$out_file_name.out 1>mes 2>bad &
# rm $out_file_name.out
fi
fi
done
}
root_dir="/home/yxli/te"
getdir $root_dir
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |
