虽然在看拓扑领域的文章中,经常提到自旋轨道耦合是很重要的,而且也经常遇到Rashba和Dresselhaus这两种不同的自旋轨道耦合,但也一直没有仔细去看过它们之间到底有什么区别与联系,在这里就从推导自旋轨道耦合的具体表达式开始,然后再详细的讨论一下这两种不同的自旋轨道耦合到底有什么不同与联系.
自旋轨道耦合推导
电子带电荷$-e$绕原子核以速度$\bf{v}$运动的时候,会存在自旋磁矩.电场对静止的磁矩是不存在相互作用的,而对运动的磁矩,电场将会与其发生相互作用,所以自旋磁矩和由原子实在该处产生的电场将产生相互作用,这就是自旋轨道相互作用的起源.
因为运动是相对的,上面的分析是将坐标系放在了原子实上面,那么接下来将坐标系放在电子上面,那么就是原子核绕着电子运动.这时候自旋轨道耦合效应可以理解为,电场$\bf{E}$以速度$-\bf{v}$运动产生一个磁场$\bf{B}$,这个磁场对自旋存在力矩的作用.磁场可以根据毕奥萨法尔定律计算
\[\boldsymbol{B}=\frac{\mu_{0} \boldsymbol{j} \times \boldsymbol{r}}{r^{3}}=\mu_{0} \varepsilon_{0}(\boldsymbol{v} \times \boldsymbol{E})\]这里$\bf{v}$是电子的速度,$\bf{E}$是原子核在电场处产生的电场.利用电场分布的径向分布形式即
\[E=\frac{1}{e} \frac{\partial V}{\partial r} \frac{r}{r}\]上式中V是原子核对电子的库伦势,利用轨道角动量关系$\bf{L}=r\times p$,及$\mathbf{p}=m\mathbf{v}$,可将磁感应强度写作
\[\boldsymbol{B}=\frac{1}{e m c^{2}} \frac{1}{r} \frac{\partial V}{\partial r} \boldsymbol{L}\label{eq2}\]上式即表示在电子坐标系中原子实在电子处产生的磁场.考虑自旋之后,自由电子的哈密顿量为
\[H=\frac{(\boldsymbol{\sigma} \cdot p)^{2}}{2 m}\]如果再考虑磁场$\mathbf{B}=\nabla\times\mathbf{A}$的存在后,动量要变成正则动量的形式$p\rightarrow p+\frac{e}{c}\mathbf{A}$,则哈密顿量变为
\[H=\frac{\left(\mathbf{\sigma} \cdot\left(\mathbf{p}+\frac{e}{c} \mathbf{A}\right)\right)^{2}}{2 m}\label{eq1}\]利用泡里算符关系式
\[(\boldsymbol{\sigma} \cdot \boldsymbol{A})(\boldsymbol{\sigma} \cdot \boldsymbol{B})=\boldsymbol{A} \cdot \boldsymbol{B}+\mathrm{i} \boldsymbol{\sigma} \cdot(\boldsymbol{A} \times \boldsymbol{B})\]将(\ref{eq1})化简为
\[H=\frac{\left(p+\frac{e}{c} A\right)^{2}}{2 m}+\frac{\mathrm{i}}{2 m} \boldsymbol{\sigma} \cdot\left(p+\frac{e}{c} \boldsymbol{A}\right) \times\left(p+\frac{e}{c} \boldsymbol{A}\right)\]第一项是电子轨道磁矩和外磁场的相互作用,这里主要关注第二项,利用矢量代数工具可将第二项化简
\(\frac{\mathrm{i} e}{2 m c} \boldsymbol{\sigma} \cdot[(\boldsymbol{p} \times \boldsymbol{A})+(\boldsymbol{A} \times \boldsymbol{p})]= \frac{\mathrm{i} e}{2 m c} \boldsymbol{\sigma} \cdot(-\mathrm{i} \hbar \nabla \times \boldsymbol{A})=\frac{e h}{2 m c} \boldsymbol{\sigma} \cdot \boldsymbol{B}=-\boldsymbol{\mu}_{s} \cdot \boldsymbol{B}\label{eq3}\) $\mathbf{\mu_s}$是自旋$\bf{S}$相对应的磁矩,根据原子物理的可以知道电子的自旋磁矩$\mathbf{\mu_s}=-g_s\mu_B\mathbf{S}$,这里$g_s$是自旋朗德g因子,玻尔磁子$\mu_B=\frac{e\hbar}{2mc}$,$\bf{S}$是自旋角动量.
将(\ref{eq2})代入(\ref{eq3})后,再利用$A \cdot(B \times C)=B \cdot(C \times A)=C \cdot(A \times B)$可以得到自旋轨道相互作用为
\[U=\frac{1}{m^{2} c^{2}} \frac{1}{r} \frac{\partial V}{\partial r} \boldsymbol{L} \cdot \boldsymbol{S}= -\frac{1}{m^{2} c^{2}} \nabla V \cdot(\boldsymbol{S} \times \boldsymbol{p})\]到这里就推导出了自旋轨道耦合的一般表达式,在考虑电子参考系的非惯性系后真空中的自旋轨道耦合哈密顿量为(什么非惯性系这个我也不懂)
\[H_{s 0}=-\frac{1}{4 m^{2} c^{2}}(\boldsymbol{\sigma} \cdot \boldsymbol{p}) \times \nabla V\]这就是经常在文章中看到的自旋轨道耦合通用形式.
Rashba自旋轨道耦合
Rashba就是在二维平面的垂直方向破坏反演对称后的结果,如果在$z$方向加上一个电场,从而在这个方向上的反演对称就会被破坏
\[H_{E}=-E_{0} z\]带电的电子以速度$v$在电场中运动时将会感受到一个有效的磁场
\[\mathbf{B}=-(\mathbf{v} \times \mathbf{E}) / c^{2}\]那么此时的自旋轨道相互作用为
\[H_{\mathrm{SO}}=\frac{g \mu_{\mathrm{B}}}{2 c^{2}}(\mathbf{v} \times \mathbf{E}) \cdot \boldsymbol{\sigma}\]所以此时的Rashba自旋轨道耦合可表示为
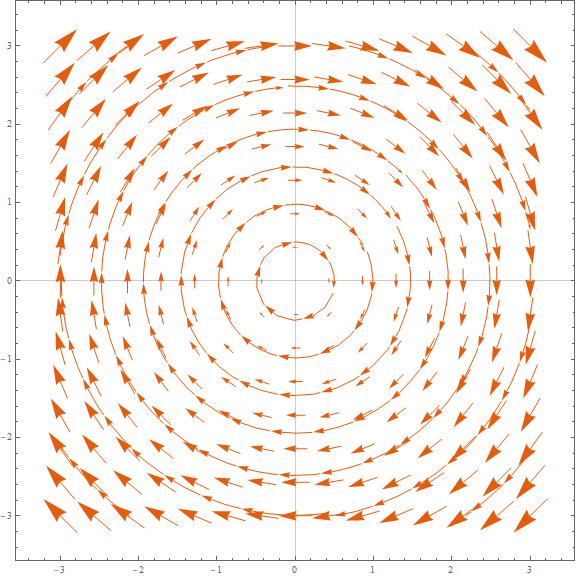
\[H_{\mathrm{R}}=-\alpha_{\mathrm{R}}(\boldsymbol{\sigma} \times \mathbf{p}) \cdot \hat{z}=-\alpha_R(\sigma_{x} p_{y}-\sigma_{y} p_{x})\]这一项前面的系数通常可以通过实验进行测量.这一项的存在就类似于此时存在一个磁场$(p_y,-p_x,0)$,这个磁场的方向和大小与动量有关,其向量图表示如下
VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}, StreamPoints -> Coarse, PlotTheme -> "Scientific", ImageSize -> Large, PlotRange -> All]
Dresselhauss自旋轨道耦合
Dresselhauss这种形式的自旋轨道耦合推导的过程比较复杂,我也没有找到合适的资料,这里只是简单的从把知乎和维基上的内容进行一下整理.这种形式的自旋轨道耦合哈密顿量通常表示为
\[H_{\mathrm{D}} \propto p_{x}\left(p_{y}^{2}-p_{z}^{2}\right) \sigma_{x}+p_{y}\left(p_{z}^{2}-p_{x}^{2}\right) \sigma_{y}+p_{z}\left(p_{x}^{2}-p_{y}^{2}\right) \sigma_{z}\]在一个2D的纳米结构中,也就是$z$方向上是有限的时候,这个哈密顿量可以分拆成线性项和三次方项 \(H_{\mathrm{D}}^{(1)}=\frac{\beta}{\hbar}\left(\sigma_{x} p_{x}-\sigma_{y} p_{y}\right)\\ H_{\mathrm{D}}^{(3)}=-\frac{\beta}{\hbar^{3}}\left(\frac{d}{\pi}\right)^{2} p_{x} p_{y}\left(p_{y} \sigma_{x}-p_{x} \sigma_{y}\right)\)
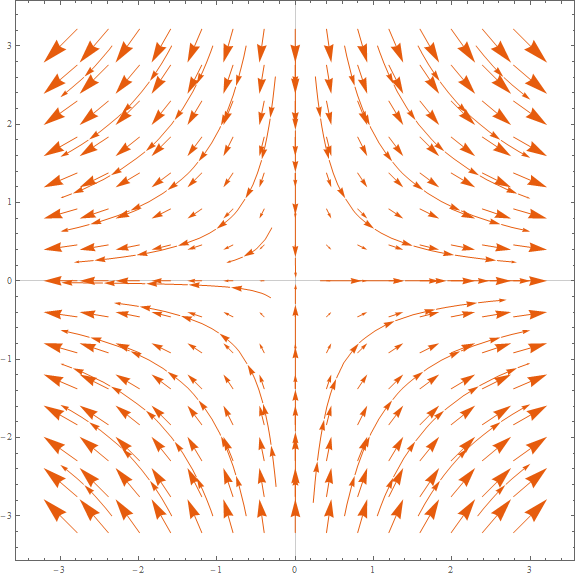
这里$\beta$是耦合常数,$d$则是材料的厚度.如果在这里只关注线性项,那么此时也有一个等效的磁场$(p_x,-p_y,0)$,其向量图如下
VectorPlot[{x, -y}, {x, -3, 3}, {y, -3, 3}, StreamPoints -> Coarse,PlotTheme -> "Scientific", ImageSize -> Large, PlotRange -> All]
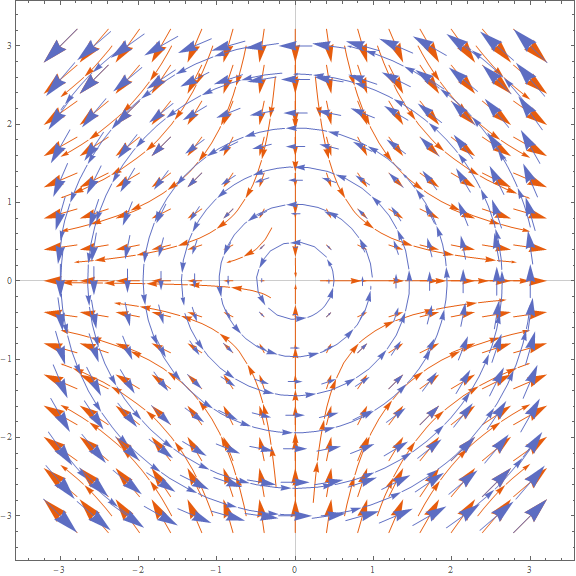
将这两不同形式的自旋轨道耦合对应的等效磁场放在一起进行比较,如下图所示
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |