Yu-Xuan Blog
  • YuXuan
  • 2020年 09月29日

表面电荷与极化多值性理解

 

在学习Berry位相与电荷极化的过程中,总算是成功的理解了便面电荷密度和电荷极化之间的联系,以及表面电荷的多值问题,这里就把自己的一些理解和写的一些代码整理出来,也加深一下自己对这个概念的理解.我这里所有的内容都是来自于Berry Phase in electronic structure theory.

在学习Berry位相与电荷极化的过程中,总算是成功的理解了便面电荷密度和电荷极化之间的联系,以及表面电荷的多值问题,这里就把自己的一些理解和写的一些代码整理出来,也加深一下自己对这个概念的理解.我这里所有的内容都是来自于Berry Phase in electronic structure theory.

极化

首先考虑一个晶体绝缘体随着时间慢慢变化,但是在这个过程中晶体的元胞仍然保持周期性.这种变化可以通过外加一个弱电场或者磁场来实现.如果这种变化引起了极化$\mathbf{P}$的改变,那么相应的就会由一个宏观的电流密度$\mathbf{J}$在晶体内部流动.

\[\mathbf{J}=\frac{d\mathbf{P}}{dt}\label{eq1}\]

接下来考虑静态情况,不过此时晶体哈密顿量随空间有一个变化,这将会导致极化$\mathbf{P}$随着宏观大小的距离$\mathbf{r}$改变,这里$\mathbf{r}$的尺度是远大于原子尺度的,这样的话就存在一个宏观的电荷密度

\[\rho(\mathbf{r})=-\nabla\cdot\mathbf{P}(\mathbf{r})\label{eq2}\]

当系统在空间和时间上都存在缓变的时候,(\ref{eq1})和(\ref{eq2})是自洽的,可以利用电荷守恒方程

\[\frac{d\rho}{dt}=-\nabla\cdot\mathbf{J}\]

现在考虑第三种情况,考虑一个静态的晶体绝缘体存在一个和表面方向$\hat{\mathbf{n}}$垂直的极化$\mathbf{P}$.这种情况下在表面上会存在束缚电荷的极化,如果此时表面是绝缘的,那么表面上就不存在自由电子.所以可以存在下列关系

\[\sigma_{surf}=\mathbf{P}\cdot\hat{\mathbf{n}}\label{eq3}\]

这里$\sigma_{surf}$就是微观的表面电荷.

(\ref{eq3})的定义,严格上来说并不是正确的表达.

png

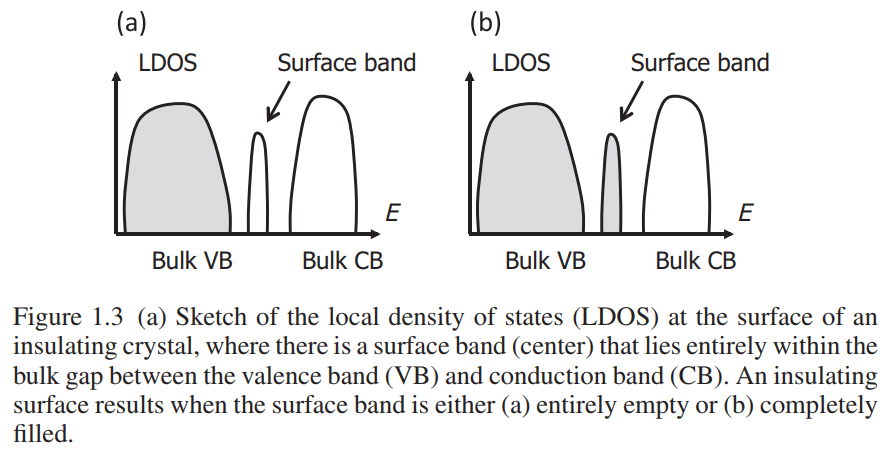
上面的这张图显示了晶体绝缘体在表面的局域态密度,左边的阴影部分代表是被占据的价带,而空白的部分则代表的是导带.在这里假设有一个表面态能带,它的宽度很小,恰好就落在了体态价带和导带能隙之间,在这里假设表面态能带是非常窄的,这样才能保证它恰好就在能隙内.有了这样的一个图像之后,对于绝缘的表面态能带,就存在两种情况,如上图所示.对于(a)图,如果费米面恰好落在体态价带与表面态能带之间,那么此时表面态能带中没有电子填充,自然表面就是绝缘性质.而对于(b)图来说,如果费米面落在表面态能带与体态导带之间,此时表面态能带式被电子满填充的,那么根据能带分析,此时表面态仍然是绝缘的.

显然对于上图中的两种情况,表面态都是绝缘属性,但是表面的电子密度却是不相同的,两种情况表面电子密度的差为$-e/A_{surf}$,这里$A_{surf}$就是表面垂直方向上$\hat{\mathbf{n}}$元胞的面积,电荷量$e>0$.

从这里就可以看到,如果还是利用(\ref{eq3})来表达表面电荷密度,那么就会出现一定的矛盾,很明显两种情况对应的表面电荷密度是不同的.所以这里需要先放弃(\ref{eq3})这种表达,但是它还是一个反映极化和表面电荷密度不错的出发点.接下来转变视角,我觉得这是我从参考书上学到最天才的方法.既然(\ref{eq3})还是一个很好的出发点,那么保留它的形式,但是这个时候电荷密度不再是等于极化在便面垂直方向上的分量,将极化的这个分量想象成一个多值函数,就好像复变函数中的很多函数,在复平面上都是周期的,存在很多的branch,而上图中(a)与(b)所表示的情况,只不过就是电荷密度落在了这个多值函数的某一个分支上而已.就是这个天才的想法,让我对这本参考书佩服的五体投地,之前学习凝聚态中的拓扑时,从来没有从这个基础,这么优美的角度分析过问题.那么既然这个时候已经表明极化在表面上的分量是个多值函数,那么与复变函数类似的做比较,它自然也是有自己的周期的,这个周期前面也已经计算出,即就是$\frac{e}{A_{surf}}$,所以可以将(\ref{eq3})改写成多值函数的形式

\[\sigma_{surf}=\mathbf{P}\cdot\hat{\mathbf{n}}\quad mod\quad \frac{e}{A_{surf}}\]

这个公式中最后取了$mod\quad \frac{e}{A_{surf}}$,也就是这个时候的表面电荷密度,到底是在多值函数的哪一个分支上.这个想法真的是非常的天才.

Riemann绘制

上面讲了这么多,如果对复变函数熟悉的话,一定可以看明白这个多值是在说什么东西,那么这里更加好看一些,所谓的有图有真相,就利用软件顺便来画画复变函数里面的黎曼面,也可以更加清楚的看到这个多值,到底是什么含义,公式中最后的取mod又如何反映取值是在多值函数的哪个分支上.

Mathematica绘制

png

Mathematica里面是没有内置函数直接可以进行黎曼面绘制的,最后还是从外部调用了已经写好的一个包,可以用来绘制黎曼面,代码如上.简单的解释一下上面的代码,它一共会画两张图,一张是函数实部的黎曼面,另一张就是虚部的黎曼面,设下的参数就仅仅是作图样式的一些简单设置.下面就画一下$\log(z)$这个函数的黎曼面

rsurf /@ {Log[z]}

png

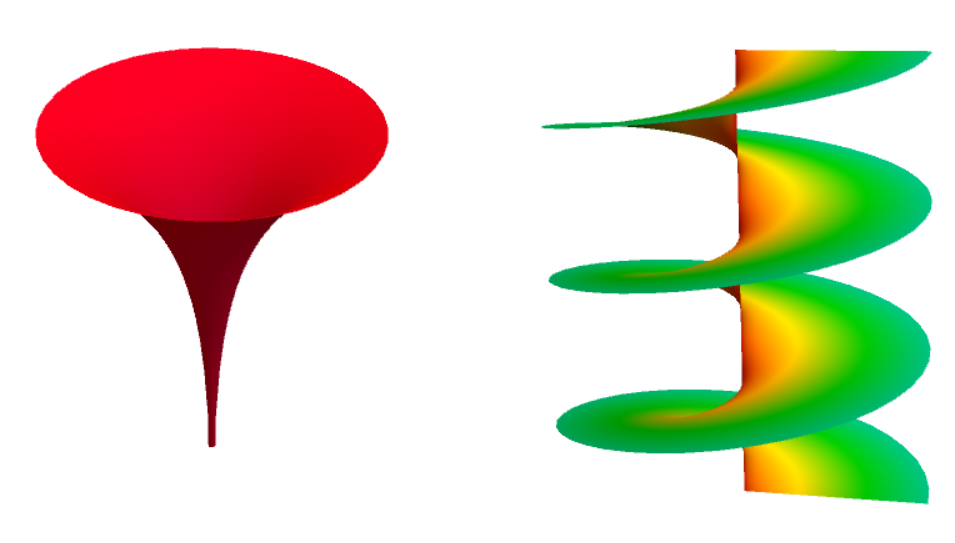
左侧是实部的黎曼面,右侧的即就是虚部的黎曼面.接下来复习一下复变函数的概念,解释一个$\log(z)$这个函数.

对于一个给定的自变量值z,凡是满足$e^w=z$的所有$w$值均称为对数函数$w=\log(z)$的函数值.它是指数函数$w=e^z$的反函数.令$w=u+iv$,$z=re^{i\theta}$,可以得到$e^ue^{iv}=re^{i\theta}$,所以有

\[u=\ln r=\ln \rvert z\rvert\qquad v=\theta + 2n\pi\quad(n=0,\pm1\pm2,\dots)\]

这样就可以把对数函数$w=\ln z$明确的表示为

\[w=\ln z=\ln\rvert z\rvert+i(\theta+2n\pi)=\ln \rvert z\rvert+i\cdot arg(z)\]

对数函数$w=\ln z$也是多值的,其多值性来源于宗量$z$辐角的多值性,多值性的表现则是函数值$w$的虚部.对应每一个$z$值,有无穷多个$w$值,它们的实部相同,虚部相差$2\pi$的整数倍.这里的分析也就正好和上面的两张图完美的对应到了一起,黎曼面的解释就到这里结束.上面的这个函数同样也可以用来绘制其它函数的黎曼面,感兴趣可以自行玩耍.

Python绘制

"""
Riemann plot of a non-Hermitian matrix
"""

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np


XR = np.arange(-1, 1, 0.01)
YR = np.arange(-1, 1, 0.01)

delta, kappa = np.meshgrid(XR, YR)

g1 = 0.2; g2 = 0.1
chi = (g1+g2)/2.0
beta = (g1-g2)/2.0
Gamma = delta + 1j*beta

disc = np.sqrt(kappa**2+Gamma**2)

lambda1 = delta-1j*chi+disc 
lambda2 = delta-1j*chi-disc 


F = plt.figure(1)
A = F.gca(projection='3d')
plt.xlabel('$\delta$')
plt.ylabel('$\kappa$')
A.set_zlabel('Re $\lambda$')
S = A.plot_surface( kappa, delta, lambda1.real, rstride=1, cstride=1, cmap=cm.Reds )
S = A.plot_surface( kappa, delta, lambda2.real, rstride=1, cstride=1, cmap=cm.Greys )

F = plt.figure(2)
A = F.gca(projection='3d')
plt.xlabel('$\delta$')
plt.ylabel('$\kappa$')
A.set_zlabel('Im $\lambda$')

S = A.plot_surface(kappa, delta, lambda1.imag, cmap=cm.Reds)
S = A.plot_surface(kappa, delta, lambda2.imag, cmap=cm.Greys)

plt.show()

由于python的用途实在太广泛了,所以这里就顺便也用python来绘制一下,不过从效果上看,好像没有Mathematica那么漂亮.

png

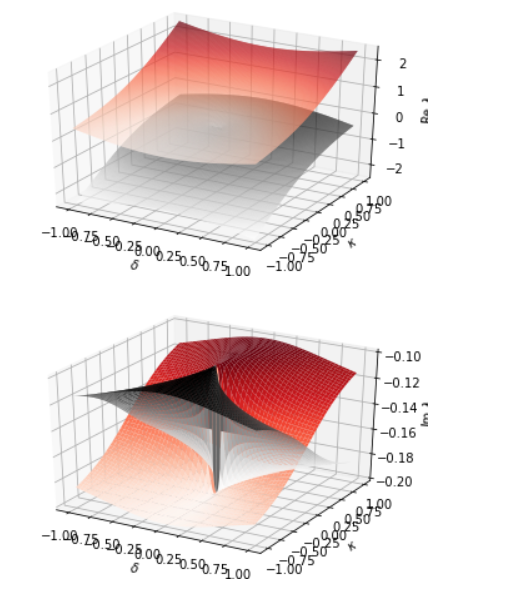
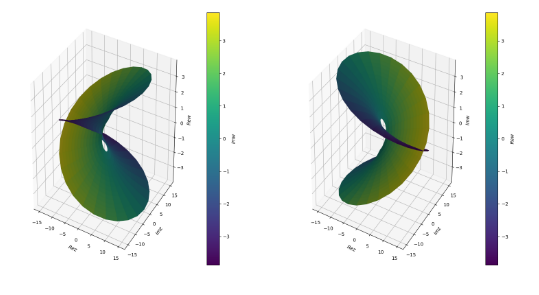
上面的绘制我觉得不够美观,所以再提供另外一个比较好看的绘图方式

import numpy as np  
import matplotlib.pyplot as plt  
import matplotlib.cm as cm 
from mpl_toolkits.mplot3d import Axes3D 
 
# compute data to plot 
r, theta = np.mgrid[1:16, -2*np.pi:2*np.pi:50j] 
z = r * np.exp(1j*theta)  
w = np.sqrt(r) * np.exp(1j*theta/2)  
 
# plot data  
fig = plt.figure()  
for plot_index in [1, 2]: 
    if plot_index == 1: 
        z_data, c_data = w.real, w.imag 
        z_comp, c_comp = 'Re', 'Im' 
    else: 
        z_data, c_data = w.imag, w.real 
        z_comp, c_comp = 'Im', 'Re' 
    c_data = (c_data - c_data.min()) / c_data.ptp() 
    colors = cm.viridis(c_data) 
 
    ax = fig.add_subplot(f'12{plot_index}', projection='3d') 
    surf = ax.plot_surface(z.real, z.imag, z_data, facecolors=colors,
                           clim=[z_data.min(), z_data.max()])
    ax.set_xlabel('$Re z$')  
    ax.set_ylabel('$Im z$')   
    ax.set_zlabel(f'${z_comp} w$')  
    cb = plt.colorbar(surf, ax=ax)  
    cb.set_label(f'${c_comp} w$')  
 
plt.show()

png

参考

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。

png