时间反演
虽然在前面对时间反演算符做过一些计算,但是对其具体的含义还有一些物理图像并没有很清晰的认识,在这里就仔细的对这个算符进行一些物理图像上的解释,同时也能够更好的理解到底时间反演是一个什么样的物理过程.
首先有一个量子态$\rvert a\rangle$,它有一个与其对应的时间反演态$\Theta\rvert a\rangle$,这里的$\Theta$就是时间反演算符,它是个反幺正的,这一点在后面会进行解释.
\[\rvert a\rangle\rightarrow\Theta\rvert a\rangle\]这里的$\Theta\rvert a\rangle$从一个更加贴切的图像上来理解的话,应该叫做运动反演态,因为所谓时间反演,就是让这个运动沿着相同的轨迹,再演化回去,回到最初的哪个状态.那么可以想象,如果是一个运动的话,其时间反演不就正好是把这个运动过程反过来进行么,这是我对这个图像浅显的理解.也就是说如果$\rvert a\rangle$对应的动量为$\mathbf{p}$,那么$\Theta\rvert a\rangle$这个时间反演态对应的动量就应该是$\mathbf{-p}$,这样才可以保证沿着原来的运动轨迹再跑回去.那么相同的,这个解释对于角动量也是试用的,这一点从角动量表达式$\mathbf{J}=\mathbf{r}\times\mathbf{p}$就可以看出.
接下来利用薛定谔绘景中的时间演化算符来对时间反演做进一步说明.假定再$t=0$时刻状态为$\rvert a\rangle$,那么再经过了时间$t=\delta t$之后系统的状态可以表示为
\[\rvert a,t_0;t=\delta t\rangle=(1-\frac{iH}{\hbar}\delta t)\rvert a\rangle\]这里的时间演化就主要是由哈密顿量H来表征的了.下面对时间反演态$\Theta\rvert a\rangle$来做时间演化
\[(1-\frac{iH}{\hbar})\Theta\rvert a\rangle\]因为$\Theta\rvert a\rangle$是$\rvert a\rangle$的时间反演态,那么上面的表达式理解成时间反演态在进行时间演化算符,它应该和下面的状态属于同一个态
\[\Theta\rvert a,t_0=0;t=-\delta t\rangle\]因为对于时间反演态,时间的演化箭头是相反的,所以这里也就是$t=-\delta t$.
综上所述可以得到
\[\left(1-\frac{i H}{\hbar} \delta t\right) \Theta\rvert a\rangle=\Theta\left(1-\frac{i H}{\hbar}(-\delta t)\right)\rvert a\rangle\]到这里就可以得到
\[-iH\Theta\rvert\rangle=\Theta i H\rvert\rangle\label{e1}\]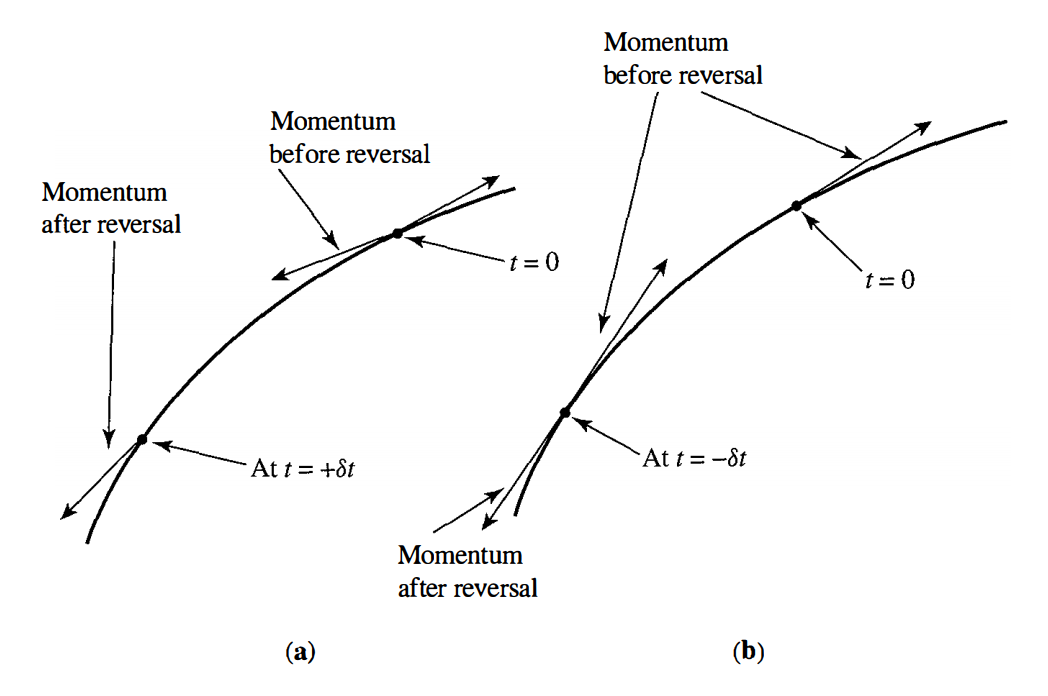
反幺正证明
在这里对时间反演是不能是幺正的进行解释.先假设时间反演是幺正的$\Theta\Theta^{-1}=1$,那么(\ref{e1})中$\Theta$对虚数$i$是没有影响的,则它可以从方程两端约去就得到
\[-H\Theta=\Theta H\]假设态$\rvert n\rangle$是$H$的本征态,其本征能量是$E_n$,那么它的时间反演态就是$\Theta \rvert n\rangle$,可以有
\[H \Theta\rvert n\rangle=-\Theta H\rvert n\rangle=\left(-E_{n}\right) \Theta\rvert n\rangle\]所以时间反演态的本征能量为$-E_n$,但是这个结果对于自由粒子来说就是有问题的,自由粒子的能量范围是$0\rightarrow\infty$,那么对应的时间反演态的能量就变成$-\infty\rightarrow 0$,这很显然是不符合物理的.同样的可以对自由粒子的动能算符进行操作
\[\Theta^{-1} \frac{\mathbf{p}^{2}}{2 m} \Theta=\frac{-\mathbf{p}^{2}}{2 m}\]很显然,从最开始的物理过程分析也能明白,时间反演态动量会相反,但是有了平方之后就会消去这个符号,而这里还是存在负号,所以从一开始假定时间反演算符是幺正的,这个出发点就是错误的,它应该是反幺正算符才对,那么如果它是反幺正算符,对于复数i肯定会有影响,则利用(\ref{e1})的表达式可以得
\[\Theta i H\rvert\rangle=-i \Theta H\rvert\rangle\]所以此时的时间反演算符是个反线性算符,上式可以化简为
\[\Theta H=H\Theta\]在上面的分析中,如果$\Theta$是个反幺正算符,对于复数有$\Theta i=-i\Theta$
时间反演与可观测量
既然已经证明了时间反演算符是反幺正的也就是非线性算符,那么在利用Dirac的态表示符号的时候,就需要注意,一般如果是对于时间反演态,不会取这样的形式$\langle \beta\rvert$,因为这种形式会将两个ket空间bra空间变的不是那么清楚,而且如果熟悉这个符号的话,就一定清楚这套符号的发展本来就是对于线性算符的,所以对于非线性算符作用,一般不这样写,而是利用下面的记号
\[\rvert \tilde{\alpha}\rangle=\Theta\rvert \alpha\rangle, \quad\rvert \tilde{\beta}\rangle=\Theta\rvert \beta\rangle\]将时间反演态直接用另外的一个态表示,这样的处理对于之后进行可观测量的计算是有一定的简化的.
假设$\otimes$是一个线性算符,那么就会有下面这个性质
\[\langle\beta\rvert \otimes\rvert \alpha\rangle=\left\langle\tilde{\alpha}\left\rvert \Theta \otimes^{\dagger} \Theta^{-1}\right\rvert \tilde{\beta}\right\rangle\]这个恒等式是对反幺正算符才会成立的.下面先定义一个量
\[\rvert \gamma\rangle \equiv \otimes^{\dagger}\rvert \beta\rangle\]那么利用ket和bra的对偶关系可以得到
\[\rvert \gamma\rangle \stackrel{\mathrm{DC}}{\leftrightarrow}\langle\beta\rvert \otimes=\langle\gamma\rvert\]所以对于一个态,计算某个物理可观测量的时候,可以和它的时间反演态相互联系起来
\[\begin{aligned} \langle\beta\rvert\otimes\rvert\alpha\rangle&=\langle\gamma\rvert\alpha\rangle=\langle\tilde{\alpha}\rvert\tilde{\gamma}\rangle\\ &=\langle\tilde{\alpha}\rvert\Theta\otimes^\dagger\rvert\beta\rangle=\langle\tilde{\alpha}\rvert\Theta\otimes^\dagger\Theta^{-1}\Theta\rvert\beta\rangle\\ &=\langle\tilde{\alpha}\rvert\Theta\otimes^\dagger\Theta^{-1}\rvert\tilde{\beta}\rangle \end{aligned}\]所以对于一个厄密的可观测量$A$,可以有下面的关系
\[\langle\beta\rvert A\rvert\alpha\rangle=\langle\tilde{\alpha}\rvert\Theta A\Theta^{-1}\rvert\tilde{\beta}\rangle\]对于一个可观测量$A$可以有$\Theta A\Theta^{-1}=\pm A$,如果取正号,那么这个观测量在时间反演下是even,否则就是odd.这个其实就是限制了算符$A$的矩阵元在时间反演情况下有一个特定的位相,即
\[\langle\beta\rvert A\rvert \alpha\rangle=\pm\langle\tilde{\beta}\rvert A\rvert \tilde{\alpha}\rangle^{*}\]如果此时$\rvert\beta\rangle=\rvert\alpha\rangle$,那么上式也就变成了算符的期望值.对于动量算符就有$\langle\alpha\rvert \mathbf{p}\rvert ,\alpha\rangle=-\langle\tilde{\alpha}\rvert \mathbf{p}\rvert \tilde{\alpha}\rangle$,所以动量算符$\mathbf{p}$在时间反演下就是odd.这也就意味着
\[\mathbf{p} \Theta\left|\mathbf{p}^{\prime}\right\rangle =-\Theta \mathbf{p} \Theta^{-1} \Theta\left|\mathbf{p}^{\prime}\right\rangle =\left(-\mathbf{p}^{\prime}\right) \Theta\left|\mathbf{p}^{\prime}\right\rangle\]对于位置算符,也可以自行进行验证,就会发现它在时间反演下是even.那么角动量$\mathbf{J}=\mathbf{r}\times\mathbf{p}$在时间反演下自然也和动量是相同的,$\Theta\mathbf{J}\Theta^{-1}=-\mathbf{J}$.
自旋在时间反演下的变化
由上面的分析可以看到,动量在时间反演下肯定是odd的,也就是有负号出现,那么自旋在时间反演下肯定也就会出现负号
\[\Theta \mathbf{S}\Theta^{-1}=-\mathbf{S}\]此时$S$是粒子的自旋算符,它可以通过Pauli矩阵表示出来.既然此时的$S$是矩阵的表达形式,那么相应的时间反演算符$\Theta$肯定也就是一个矩阵表达,而在前面的分析中已经知道,时间反演算符是个反幺正的,也就是非厄密算符,它对一个复数$i$有取共轭的作用,所以此时将时间反演算符写成$\Theta=U\mathcal{K}$这里将取共轭的部分吸收到$\mathcal{K}$中,$\mathcal{K}i=-i$,那么剩下的$U$就是一个矩阵,可以通过对自旋算符的作用将这个矩阵完全求解出来.
\[\Theta \mathbf{S}\Theta^{-1}=U\mathcal{K}\mathbf{S}\mathcal{K}^{-1}U^{-1}=U\mathbf{S}^*U^{-1}\]在$S_z$的表象中,$S_x,S_z$都是实数矩阵,$S_y$是复数矩阵,所以可以得到
\[US_xU^{-1}=-S_x,\quad US^*_yU^{-1}=S_y,\quad US_zU^{-1}=-S_z\]因为$2\times 2$的矩阵,其实$S_i$就已经构成这个空间中的完备基矢,所以可以将这个$U$求解出来
\[U=i\sigma_y,\quad U=-i\sigma_y\]所以对于时间反演算符,还具有$\Theta^2=-1$这一性质.
时间反演作用在自旋上$\Theta \mathbf{S}\Theta^{-1}=-\mathbf{S}$可以看做是绕着某一个轴转动了$\pi$的角度,通常选择$y$轴,那么时间反演操作算符为
\[\mathcal{T}=e^{-i\frac{\pi S_y}{\hbar}}\mathcal{K}\]这里的$\mathcal{K}$表示复共轭,$\mathcal{T}$的平方为
\[\begin{equation}\begin{aligned}\mathcal{T}^2&=e^{-i\frac{\pi S_y}{\hbar}}\mathcal{K}e^{-i\frac{\pi S_y}{\hbar}}\mathcal{K}\\&=e^{-i\frac{\pi S_y}{\hbar}}e^{i\frac{\pi S^*_y}{\hbar}}\\&=e^{-2i\frac{\pi S_y}{\hbar}}\end{aligned}\end{equation}\]对于复共轭操作$\mathcal{K}^2=1$,对于整数自旋,$S_y$的本征值是$\hbar$的整数倍,总可以得到$\mathcal{T}^2=1$,与spinless的情况一致,但是对于半整数自旋的系统
\[e^{-i\frac{\pi S_y}{\hbar}}=e^{-i\frac{\pi \sigma_y}{2}}=\sum_n^\infty\frac{1}{n!}(-\frac{i\pi\sigma_y}{2})^n=-i\sigma_y\]从而可以有$\mathcal{T}^2=-1$.时间反演算符对半整数自旋系统的作用为
\[\mathcal{T}c_{j,\alpha,\sigma}\mathcal{T}^{-1}=i(\sigma_y)_{\sigma,\sigma^{'}}c_{j,\alpha,\sigma^{'}}\]即满足
\[\mathcal{T}c_{j,\alpha,\uparrow}\mathcal{T}^{-1}=c_{j,\alpha,\downarrow}\] \[\mathcal{T}c_{j,\alpha,\downarrow}\mathcal{T}^{-1}=-c_{j,\alpha,\uparrow}\]Kramers 定理
既然系统存在时间反演不变,那么自然可以介绍一下Kramers定理,这个定理告诉我们,所有的能量本征值,最少是两重简并的.从哈密顿量对角化的角度来说,也就是每一个本征值都必定出现两次,但是它们对应的本征态却是不同的.下面可以通过反证法来证明.假设有两个态$\rvert u\rangle$,$\rvert v\rangle=\mathcal{T}\rvert u\rangle$,这里$\mathcal{T}$是时间反演算符,$\rvert v\rangle$则是$\rvert u\rangle$的时间反演态,它应该和$\rvert u\rangle$具有相同的本征值.哈密顿量具有时间反演即满足
\[\mathcal{T}H=H\mathcal{T}\]若$H\rvert u\rangle=E\rvert u\rangle$,$E$是哈密顿量本征值,定位实数,则
\[H(\mathcal{T}\rvert u\rangle)=\mathcal{T}H\rvert u\rangle=\mathcal{T}E\rvert u\rangle\]假设没有简并出现,那么$\rvert v\rangle$和$\rvert u\rangle$之间仅仅就相差一个位相因子$\rvert v\rangle=e^{i\varphi}\rvert u\rangle$,利用时间反演算符$\mathcal{T}^2$作用到$\rvert u\rangle$可得$\mathcal{T}^2\rvert u\rangle=\mathcal{T}e^{i\varphi}\rvert u\rangle=e^{-i\varphi}\mathcal{T}\rvert u\rangle=\rvert u\rangle$,这里利用了关系式$\mathcal{T}\rvert u\rangle=\rvert v\rangle=e^{i\varphi}\rvert u\rangle$,所以从假设出发,推导出了和$\mathcal{T}^2=-1$相矛盾的结果,那么就说明一开始的假设式错误的,所以$\rvert u\rangle$和$\rvert v\rangle$一定是两个不同的简并态,它们之间并不只是简单的相差一个位相因子,但是这两个态的能量确实是相同的.综上分析可以得到$\mathcal{T}\rvert u\rangle=\rvert v\rangle,\mathcal{T}\rvert v\rangle=-\rvert u\rangle$
当自旋轨道耦合(SOC)比较弱的时候,可以认为自旋还是一个好的量子数,可以把spin-up和spin-down的电子看作是时间反演对,但是这个看法在SOC比较强的时候就不可成立,因为较强的自旋轨道耦合已经使得自旋不再使个好量子数.
参考
- 1.Modern Quantum Mechanic
- 2.高等量子力学(喀兴林)
- 2.Berry Phases in Electronic Structure Theory
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |