在固体物理中,Bloch定理使非常重要的,这也是我们可以将阿伏伽德罗常数多的体系进行求解的一个重要起点,主要就是因为晶体是由一系列具有周期性的结构组成,那么势场自然也就有周期性,从而就有了Bloch定理,在这里就主要想写一些自己最近在学此过程中对这个定理的进一步认识,同时也主要理解一下Cell波函数在这里的作用.
Bloch定理
对于理想晶体,原子排列成晶格,晶格具有周期性,从而等效的势场$V(\mathbf{r})$也具有周期性,晶体中的电子就是在一个具有周期性的等效势场中运动的,满足方程
\[[-\frac{\hbar^2}{2m}\nabla^2+V(\mathbf{r})]\psi=E\psi\\ V(\mathbf{r})=V(\mathbf{r+R_n})\]这里$\mathbf{R_n}$是任意晶格矢量.
Bloch定理就是,当势场具有周期性的时候,波动方程的解$\psi$具有如下性质
\[\psi_{n\mathbf{k}}(\mathbf{r+R_n})=e^{i\mathbf{k}\cdot\mathbf{R_n}}\psi_{n\mathbf{k}}(\mathbf{r}) \label{eq1}\]其中$\mathbf{k}$为一矢量.(\ref{eq1})表明当平移晶格矢量$\mathbf{R_n}$时,波函数只增加了位相因子$e^{i\mathbf{k}\cdot\mathbf{R_n}}$,(\ref{eq1})也就是Bloch定理,根据Bloch定理,可以把波函数写作
\[\psi_{n\mathbf{k}}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{R_n}}u_{n\mathbf{k}}(\mathbf{r})\label{eq2}\]其中$u(\mathbf{r})$具有和晶体相同的周期性,即
\[u_{n\mathbf{k}}(\mathbf{r+R_n})=u_{n\mathbf{k}}(\mathbf{r})\](\ref{eq2})表达的波函数称为Bloch函数,它是平面波与周期函数的乘积.
周期规范条件
在动量空间中,如果将问题限制在第一布里渊区,那么如果动量$\mathbf{k}$变化一个倒空间格矢,则可以有
\[\rvert \psi_{\mathbf{k+G}}\rangle=e^{i\eta(\mathbf{k})}\rvert\psi_{n\mathbf{k}}\rangle\]这里的$\mathbf{G}$是倒空间的一个格矢,连接着边界上的两个态.这里额外的位相因子并不重要,它并不会影响态的物理解释,故可以通过人为的方式来选择这个位相,在这里取位相因子是幺正的,也就是所谓的周期规范条件
\(\rvert \psi_{n,\mathbf{k+G}}\rangle=\rvert\psi_{n\mathbf{k}}\rangle\)
Cell 波函数
从上面的内容可以看到,虽然Bloch函数将晶体能带的计算大大简化了,但是在BZ边界上,Bloch波函数存在着位相因子的问题,这个在实际的计算中还是会有一定的不方便,所以通常为了方便总是选取Bloch波函数的周期部分来计算
\[u_{n \mathbf{k}}(\mathbf{r})=e^{-i \mathbf{k} \cdot \mathbf{r}} \psi_{n \mathbf{k}}(\mathbf{r})\]这个cell波函数的周期性为
\[u_{n \mathbf{k}}(\mathbf{r}+\mathbf{R})=u_{n \mathbf{k}}(\mathbf{r})\]平移一个倒空间的格矢$\mathbf{G}$后,在周期规范条件下有
\[u_{n, \mathbf{k}+\mathbf{G}}(\mathbf{r})=e^{-i \mathbf{G} \cdot \mathbf{r}} u_{n \mathbf{k}}(\mathbf{r})\]cell波函数与Bloch波函数的不同之处在于,所有的cell波函数$u_{n\mathbf{k}}$都属于定义在元胞上的周期函数的相同希尔伯特空间内.这个性质体现为对cell波函数求梯度$\nabla_\mathbf{k}u_{n\mathbf{k}}$它是属于同一个希尔伯特空间中具有良好定义的周期函数,然而对于Bloch波函数$\nabla_\mathbf{k}\psi_{n\mathbf{l}}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}[\nabla_\mathbf{k}u_{n\mathbf{k}}(\mathbf{r})+i\mathbf{r}u_{n\mathbf{k}}(\mathbf{r})]$它并具有和cell波函数相同性质,所以通常都是利用cell波函数$u_{n\mathbf{k}}(\mathbf{r})$而不是Bloch波函数$\psi_{n\mathbf{k}}(\mathbf{r})$来定义Berry位相和其它与Bloch波函数相关量的计算.这两个函数之间联系可以直观的通过图来观察
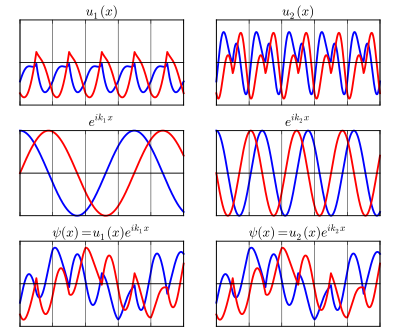
现在可以将体系的哈密顿量也变换成与动量$\mathbf{k}$相关的形式,变换方式如下
\[\begin{array}{c} H_{\mathbf{k}}=e^{-i \mathbf{k} \cdot \mathbf{r}} H e^{i \mathbf{k} \cdot \mathbf{r}} \\ H_{\mathbf{k}}\left|u_{n \mathbf{k}}\right\rangle=E_{n \mathbf{k}}\left|u_{n \mathbf{k}}\right\rangle \end{array}\]将哈密顿量变换之后,cell波函数就成了它的本征态,对应的本征值为$E_{n\mathbf{k}}$.例如对于$H=p^2/2m+V(r)$变换为
\[H_{\mathbf{k}}=\frac{(\mathbf{p}+\hbar \mathbf{k})^{2}}{2 m}+V(\mathbf{r})\]相对应的,单粒子的算符$\mathcal{O}$也要相应的进行变化$\mathcal{O}_\mathbf{k}=e^{-i\mathbf{k}\cdot\mathbf{r}}\mathcal{O}e^{i\mathbf{k}\cdot\mathbf{r}}$,算符的期望值为
\[\langle\mathcal{O}\rangle=\frac{1}{N} \sum_{n \mathbf{k}}\left\langle\psi_{n \mathbf{k}}|\mathcal{O}| \psi_{n \mathbf{k}}\right\rangle_{\mathrm{cell}}=\frac{1}{N} \sum_{n \mathbf{k}}\left\langle u_{n \mathbf{k}}\left|\mathcal{O}_{\mathbf{k}}\right| u_{n \mathbf{k}}\right\rangle\]这个变换类似于薛定谔表象与海森表表象的算符变换关系,可以参考Schrodinger,Heisenberg,Interaction绘景的区别与联系.
结语
到这里,我也对平时碰到的哈密顿量有了一个清晰的认识.无论是在量子力学还是固体物理中,哈密顿量的引入都是$H=p^2/2m+V(\mathbf{r})$的形式,但是在我阅读文献的时候,将哈密顿量进行二次量子化处理之后,最后看到的也都是$H(\mathbf{k})$这种形式,从这里总算是搞明白这两中不同形式的哈密顿量之间到底是有什么样的联系.
关于这个cell波函数的应用,我也正在学习过,通过它可以用来计算拓扑不变量,之后我也会将利用这个波函数计算拓扑不变量的方法进行整理.
参考
- 1.固体物理(黄昆)
- 2.Berry Phases in Electronic Structure Theory
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |