平时说到周期边界条件,如果对固体物理熟悉的话,第一时间想到的就是Bron-Von Karman边界条件,这就将实空间和动量空间联系了起来,但是有时候我们并不要在动量空间中研究问题,而是要在实空间研究体系Bulk的性质,那么我们就需要实现一个实空间的周期边界条件,这里我就整理一下如何对实空间的哈密顿量(紧束缚近似)实现这样的周期边界条件.

p-wave 超导体Vortex中的Majorana zero mode

我之前的一篇博客p-wave 超导体Vortex中的Majorana zero mode,就是要在实空间中利用周期边界条件,来研究一些问题.在那篇的手册中,对于周期边界到底如何设置,并没有做出很详细的描述,而这里我就将这个问题重新整理,仔细分解如何构建这样的一个周期边界.

hopping

其实在实空间中,如何设置周期边界条件的主要问题就是,对于实空间哈密顿量中的hopping项$C^\dagger_iC_j(i\ne j)$到底跳到哪一个格点上.首先放一张示意图,展示一下hooping项,以及周期边界下的拓扑结构.

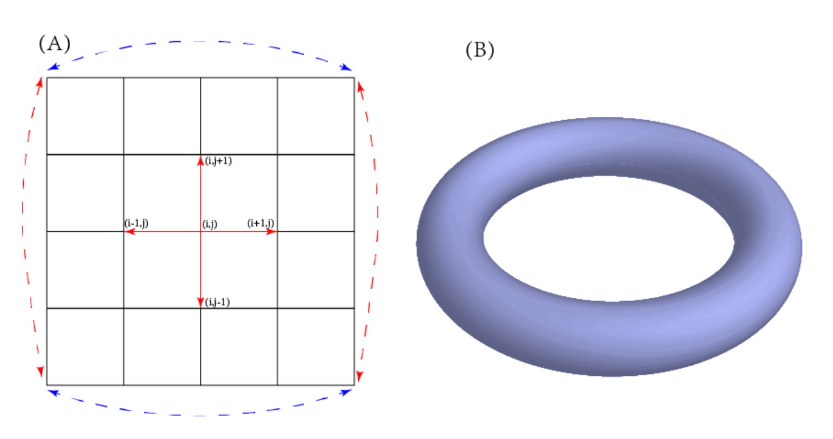
对于一个二维的系统,只有$x,y$两个方向,如果将这两个方向都设成周期的,那么就可以形成一个圆环面.

对于不处在边界上的格点,存在4个方向上的hopping,如图所示.如果将格点进行编号,假设$x$方向与$y$的格点数目分别为$x_n$和$y_n$,那么总的格点数目就是$x_n\times y_n$.假设一个不在边界上的格点其索引为$i$,那么它向右hopping即$C^\dagger_{i+1}C_i$,就代表索引要从$i$变成$i+1$,那么类似的如果是向左hopping,索引变化为$i\rightarrow (i-1)$.

接下来就是$y$方向的hopping,还是以$i$为起点,如果向$y$的正方向hopping,那么$i\rightarrow (i+y_n)$,向$y$的负方向hopping则有$i\rightarrow (i-y_n)$.这些就是不在边界上点的4个方向hopping.下面分析边界上的点如何进行hopping.

如果一个点处在最右端,为了构成周期边界条件,它向右hopping应该回到最左端$x_n\rightarrow 1$,相应的如果是最左端的格点,它向左hopping的时候,就应该是跳到最右端$1\rightarrow x_n$.对于处在上边界上的格点,它向上的hopping要跳到下边界$i\rightarrow i-(x_n-1)\times yn$,对应下边界上的点,向下hopping要到上边界,索引变化为$i\rightarrow i+(x_n-1)\times y_n$.

这个跳跃方式在我现在的角度来看,肯定就是比较简单的,但是对于初学者,最好还是画一个小的正方点阵,进行标号之后,对上面所说的这个编号索引的变化进行计算.不亲自算一下,看这些东西还是很抽象的,可能不明白我在说什么.

对于上面的索引计算,我自己利用Mathematica写了个程序,对于正反点阵,只需要改改点阵大小就可以快速的将所有方向上hopping索引的位置都计算出来

由于Mathematica的代码放在博客中总会出现奇奇怪怪的问题,导致编译不过,所以我单独将代码放在了这里.我上面所说的这种周期边界hopping同样也可以通过Fortran来写一个简单的小程序,将所有这些索引变化进行计算

subroutine boundary()
integer ix,iy,i
integer xn,yn,len2
parameter(xn = 10,yn = 10,len2 = xn*yn)
integer bry(4,len2)
do iy = 1,yn
    do ix = 1,xn
        i = (iy - 1)*xn + ix
        bry(1,i) = i + 1
        if(ix==xn)bry(1,i) = bry(1,i) - xn
        bry(2,i) = i - 1
        if(ix==1)bry(2,i) = bry(2,i) + xn
        bry(3,i) = i + xn
        if(iy==yn)bry(3,i) = bry(3,i) - len2
        bry(4,i) = i - xn
        if(iy==1)bry(4,i) = bry(4,i) + len2
    end do
end do
return
end subroutine boundary

如果相对这个周期边界的设置想进一步了解,可以参考前面这篇博客p-wave 超导体Vortex中的Majorana zero mode,里面有我重复博客中提到的文章的代码的地址,和一份更加详细的代码解释的手册,希望可以有帮助

开边界条件

既然周期边界都设置好了,那么就顺便提及一下开边界的问题,很简单,只需要将上面关于周期边界hopping的那些项设置为0即可.也就说熊最左边到最右边,从最右边到最左边,最上边到最下边,最下边到最上边,这四个边界上的这种hopping现在设置为0,那么自然就是开边界条件了.说这个是因为如果计算3D体系的时候,如果要计算体边对应关系的能带图,可能就需要在两个方向上开边界,而另外一个方向上保持周期条件,这个设置进行类比即可.

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。