在之前的学习中,仅仅知识对紧束缚的概念有一个简单的认识,并将Bloch波函数与Wannier波函数之间的联系搞清楚了,这里我想从具体一个材料出发,根据局域的原子轨道来构建系统的哈密顿量,并从这个角度更加深入的理解紧束缚近似模型.

轨道选择

png

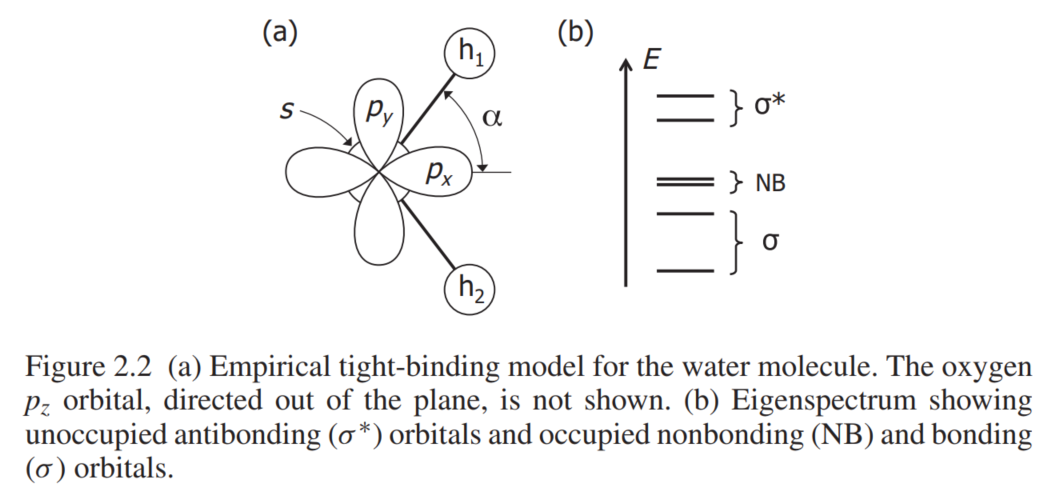
首先来看最简单的水分子的模型,在这个分子中,也可以认为这就是通常所说的元胞,这个元胞中有1个氧原子,2个氢原子,为了比较精确的描述这个体系,在这个分子中,考虑氧原子贡献$s$轨道和$p$轨道,氢原子则只能贡献$s$轨道.对于氧原子的$p$轨道,它有3个不同的取向$p_x,p_y,p_z$,那么加上两个氢原子各贡献1个$s$轨道,那么整体考虑下来,总共是有6个轨道,如果对紧束缚了解的话,就会明白在构建哈密顿量矩阵表达的时候,这个矩阵就是$6\times 6$的大小.

将这6个轨道进行标记$\rvert s\rangle,\rvert p_x\rangle,\rvert p_y\rangle,\rvert p_z\rangle,\rvert h_1\rangle,\rvert h_2\rangle$.以$\rvert s\rangle$和$\rvert h_1\rangle$为基准线,这两个轨道之间的hopping为$t_s=\langle s\rvert H\rvert h_1\rangle=\langle s\rvert H\rvert h_2\rangle$,$\rvert h_1\rangle$轨道与$\rvert p_x\rangle$轨道之间的夹角为$\alpha$,那么它们之间的hopping大小为$t_p\cos(\alpha)$;至于与$\rvert h_2\rangle$之间的hopping则可以通过简单三角函数关系得到.

我们的目的是以$\rvert s\rangle,\rvert p_x\rangle,\rvert p_y\rangle,\rvert p_z\rangle,\rvert h_1\rangle,\rvert h_2\rangle$这6个轨道,来构建矩阵$H_{ij}=\langle\varphi_i\rvert H\rvert\varphi_j\rangle$,通过上面的hopping大小分析之后,设氧原子$s$轨道的占位能为$E_s$,$p$轨道占位能为$E_p$,氢原子$s$轨道的占位能为$E_h$.则可以得到矩阵为

\[H_{\mathrm{H}_{2} \mathrm{O}}=\left(\begin{array}{cccccc} E_{s} & 0 & 0 & 0 & t_{s} & t_{s} \\ 0 & E_{p} & 0 & 0 & t_{p} \cos \alpha & t_{p} \cos \alpha \\ 0 & 0 & E_{p} & 0 & t_{p} \sin \alpha & -t_{p} \sin \alpha \\ 0 & 0 & 0 & E_{p} & 0 & 0 \\ t_{s} & t_{p} \cos \alpha & t_{p} \sin \alpha & 0 & E_{h} & 0 \\ t_{s} & t_{p} \cos \alpha & -t_{p} \sin \alpha & 0 & 0 & E_{h} \end{array}\right)\]

这里谈谈我对紧束缚近似的理解:其实首先就是寻找到最小单元元胞(对于水分子就更简单了),接下来就是分析哪些原子的哪些轨道应该是需要进行考虑的,因为原则上来说,你选取的轨道越多,自然拟合的更好,但是在固体物理中,通常费米面附近的能带才是需要更加关注的,所以肯定是尽量选择那些靠近费米面的能带(这里的能带也就是轨道形成的,每个轨道在考虑晶体的周期性之后,可以简单的认为它就形成了能带,所以有时候在看文献的过程中常说$p_x,d_{xy}$能带,其实说的就是在元胞中考虑时候的哪个轨道形成的).在选择好了合适的轨道后,那些轨道的数量就是k空间哈密顿量的维数,这一点从上面水分子的分析就可以明白,因为你需要算不同轨道之间的overlap,所以自然这个矩阵的大小就和选取的轨道数目相关了.所以可以说这些局域的原子轨道其实就对应着固体理论中的Wannier轨道,都是局域化的,而且也满足正交关系.

PythTB计算水分子

这里利用PythTB这个包来计算一下水分子的紧束缚模型,顺便加点注释,解释一些这个包到底要怎么使用,至于如何安装请参考官网

首先从pythtb中导入所需要的函数和类from pythtb import *

#!/usr/bin/env python
from __future__ import print_function # python3 style print
# ----------------------------------------------------------
# Tight-binding model for H2O molecule
# ----------------------------------------------------------
# import the pythtb module
from pythtb import *
import numpy as np

接下来就是一些简单的参数定义

# geometry: bond length and half bond-angle
b=1.0; angle=54.0*np.pi/180
# site energies [O(s), O(p), H(s)]
eos=-1.5; eop=-1.2; eh=-1.0
# hoppings [O(s)-H(s), O(p)-H(s)]
ts=-0.4; tp=-0.3

下面就是定义坐标系,这里水分子是个三维的结构,所以可以简单的就选用3维的直角坐标

# define frame for defining vectors: 3D Cartesian  建立一个坐标系，直角也好，利用元胞基矢建立也可以，
# 它的主要目的就是用来确定元胞中不同原子的相对位置到底是怎么样的
lat=[[1.0,0.0,0.0],[0.0,1.0,0.0],[0.0,0.0,1.0]] 

在确定了坐标系之后,那么接下来就是要确定水分子的6个轨道分别处在什么位置,从下面的行医可以看到,氧原子的4个轨道位置都是相同的,这是肯定的,毕竟它们是由同一个氧原子贡献的,而两个氢原子贡献的$s$轨道的位置则是不同的,设置如下

# define coordinates of orbitals: O(s,px,py,pz) ; H(s) ; H(s)
orb=[ [0.,0.,0.], [0.,0.,0.], [0.,0.,0.], [0.,0.,0.],  # 这里一共使用6个轨道，所以需要将这个6个轨道在以上面坐标系为基础上来明确这些
[b*np.cos(angle), b*np.sin(angle),0.],                 # 轨道的位置
[b*np.cos(angle),-b*np.sin(angle),0.] ]

设置好了元胞和每个轨道的位置之后,就可以来构建模型了,具体模型参数的含义已经写在代码注释中

# define model
my_model = tbmodel(0,3,lat,orb)  # 设置k空间是0维的,这里就只是计算1个水分子,不存在周期性,则k空间维度自然就是0
# 实空间是3维的，也就说完全是在实空间考虑,实空间有x,y,z三个方向,没有所谓的周期边界，三个方向都是开边界
my_model.set_onsite([eos,eop,eop,eop,eh,eh])  # 设置轨道onsite的能量，也就是占位能
my_model.set_hop(ts,0,4)  # 设置不同轨道之间的hopping大小,这里的后两个参数是轨道的索引,0代表第一个轨道,4代表第5个轨道,也就说第四个轨道
                        # 到第五个轨道的hopping大小维tx
my_model.set_hop(ts,0,5)
my_model.set_hop(tp*np.cos(angle),1,4)
my_model.set_hop(tp*np.cos(angle),1,5)
my_model.set_hop(tp*np.sin(angle),2,4)
my_model.set_hop(-tp*np.sin(angle),2,5)
# print model
my_model.display()  # 模型设置完成之后，打印模型的信息
# solve model
(eval,evec) = my_model.solve_all(eig_vectors=True)  # 对设置好的模型进行求解，并同时要求得到对应的本征矢量
# the model is real, so OK to discard imaginary parts of eigenvectors
evec = evec.real
# optional: choose overall sign of evec according to some specified rule
# (here, we make the average oxygen p component positive)
for i in range(len(eval)):
    if sum(evec[i,1:4]) < 0:
        evec[i,:]=-evec[i,:]
# print results, setting numpy to format floats as xx.xxx
np.set_printoptions(formatter={'float': '{: 6.3f}'.format})
# print eigenvalues and real parts of eigenvectors, one to a line
print(" n eigval eigvec")
for n in range(6):
    print(" %2i %7.3f " % (n,eval[n]), evec[n,:])

最终计算得到的6个轨道的能量和其对应的本征矢量结果如下

n   eigval  eigvec
-1.896  [ 0.802  0.201 -0.000  0.000  0.398  0.398]
-1.458  [ 0.000 -0.000  0.800 -0.000  0.424 -0.424]
-1.242  [-0.342  0.927  0.000 -0.000  0.110  0.110]
-1.200  [-0.000  0.000  0.000  1.000  0.000 -0.000]
-0.742  [-0.000 -0.000  0.600  0.000 -0.566  0.566]
-0.562  [ 0.490  0.317  0.000  0.000 -0.574 -0.574]

参考

1.Berry Phases in Electronic Structure Theory

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。

png

上篇实空间哈密顿量的周期边界设置

下篇Wilson Loop计算