打卡11月的第一个任务,在前面的博客中提到过计算拓扑不变量的问题,利用Wilson Loop的方法可以很好的将规范选择问题避免,最近正好在看一篇高阶拓扑半金属的文章,正好学习一下如何利用Wilson loop来计算拓扑不变量.
前言
在这里就不阐述到底如何计算Wilson loop,它与Wannier Center的关系可以看我的这篇博客通过Wannier Center计算体系Z2拓扑不变量,我所有的内容也是从Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection中学习的,感兴趣可以参考这篇文章,你也可以将哈密顿量换成BHZ模型,遮掩过就可以计算文章中的结果.
我这里势利用了Higher-Order Weyl Semimetals中的哈密顿量,因为自己正在看这篇文章,正好也可以学习一下如何计算Wilson loop.
代码实现
using LinearAlgebra,PyPlot,DelimitedFiles
# =====================================================
function hamset(kx::Float64,ky::Float64,kz::Float64)::Matrix{ComplexF64}
# 构造系统哈密顿量
t1::Float64 = 0.2
t2::Float64 = 0.24
gam::Float64 = 0.5
lam::Float64 = 1.0
ham = zeros(ComplexF64,4,4)
ham1 = zeros(ComplexF64,4,4)
#----------------------------
ham[1,2] = (1 + exp(-1im*kz))*(t1 + t2*exp(-1im*(kx + ky)))
ham[1,3] = gam + lam*exp(-1im*kx)
ham[1,4] = gam + lam*exp(-1im*ky)
ham[2,3] = exp(1im*kz)*(gam + lam*exp(1im*ky))
ham[2,4] = gam + lam*exp(1im*kx)
ham[3,4] = (1 + exp(-1im*kz))*(t1 + t2*exp(-1im*(-kx + ky)))
#-----------------------------------------------------------
ham1 = ham + ham'
return ham1
end
# ======================================================================
function main(kz)
nx::Int64 = 100
ny::Int64 = 800
Noccu::Int64 = 2 # 占据态数目
Kx = range(0,2,length = nx)
Ky = range(-1,0.9999,length = ny)
klist = []
Wave = zeros(ComplexF64,4,4,nx)
Wan = zeros(ComplexF64,Noccu,Noccu)
ang = zeros(Float64,ny,Noccu)
for iy in 1:ny
ky = Ky[iy]*pi
append!(klist,ky)
for ix in 1:nx # 在固定ky的时候,对每一个kx进行对角化
kx = Kx[ix]*pi
ham = hamset(kx,ky,kz)
val,vec = eigen(ham)
Wave[:,:,ix] = vec[:,:] # 存储所有点上的本征矢量
end
Wave[:,:,nx] = Wave[:,:,1] # 首尾相连
F = 1
for i1 in 1:nx-1
for i2 in 1:Noccu
for i3 in 1:Noccu
Wan[i2,i3] = Wave[:,i2,i1]'*Wave[:,i3,i1 + 1] # 计算Berry联络
end
end
F = F*Wan
end
val,vec = eigen(F)
ang[iy,:] = map(angle,val)/(2*pi)
end
return klist,ang
end
# =================================================================
k,ang = main(0.2*pi)
plot(k,ang)
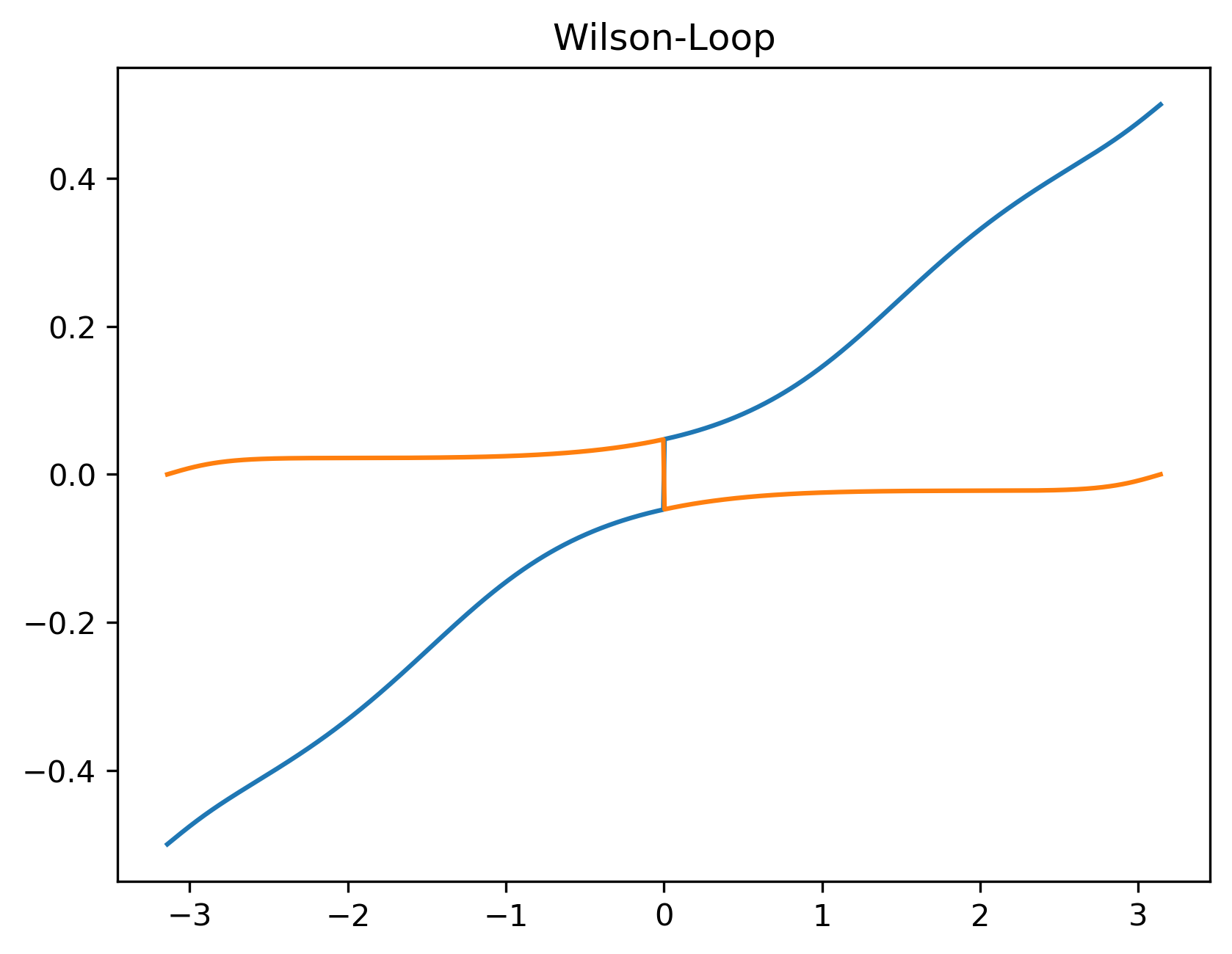
参考
- 1.Berry Phases in Electronic Structure Theory
- 2.Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection
- 3.Higher-Order Weyl Semimetals
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |