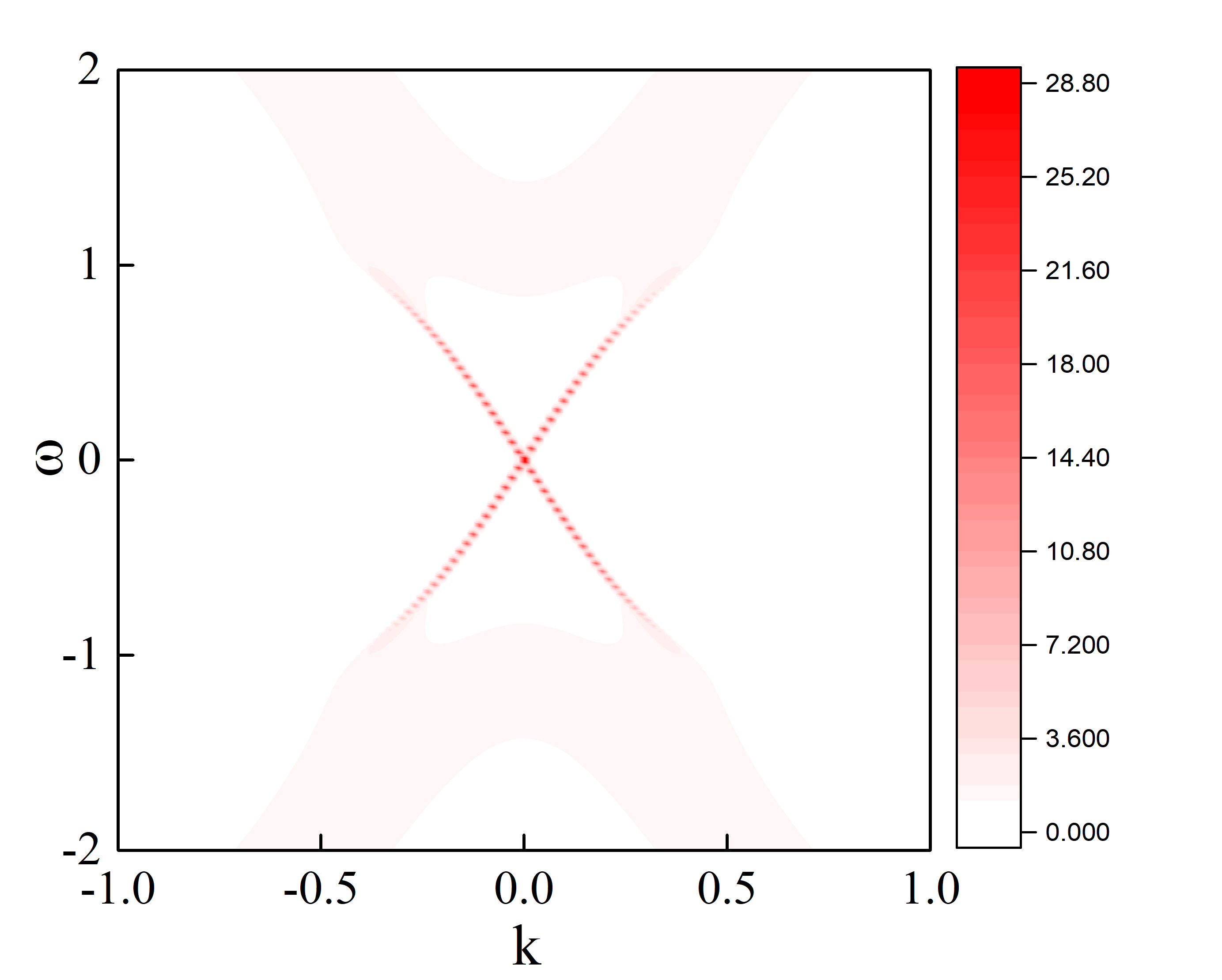
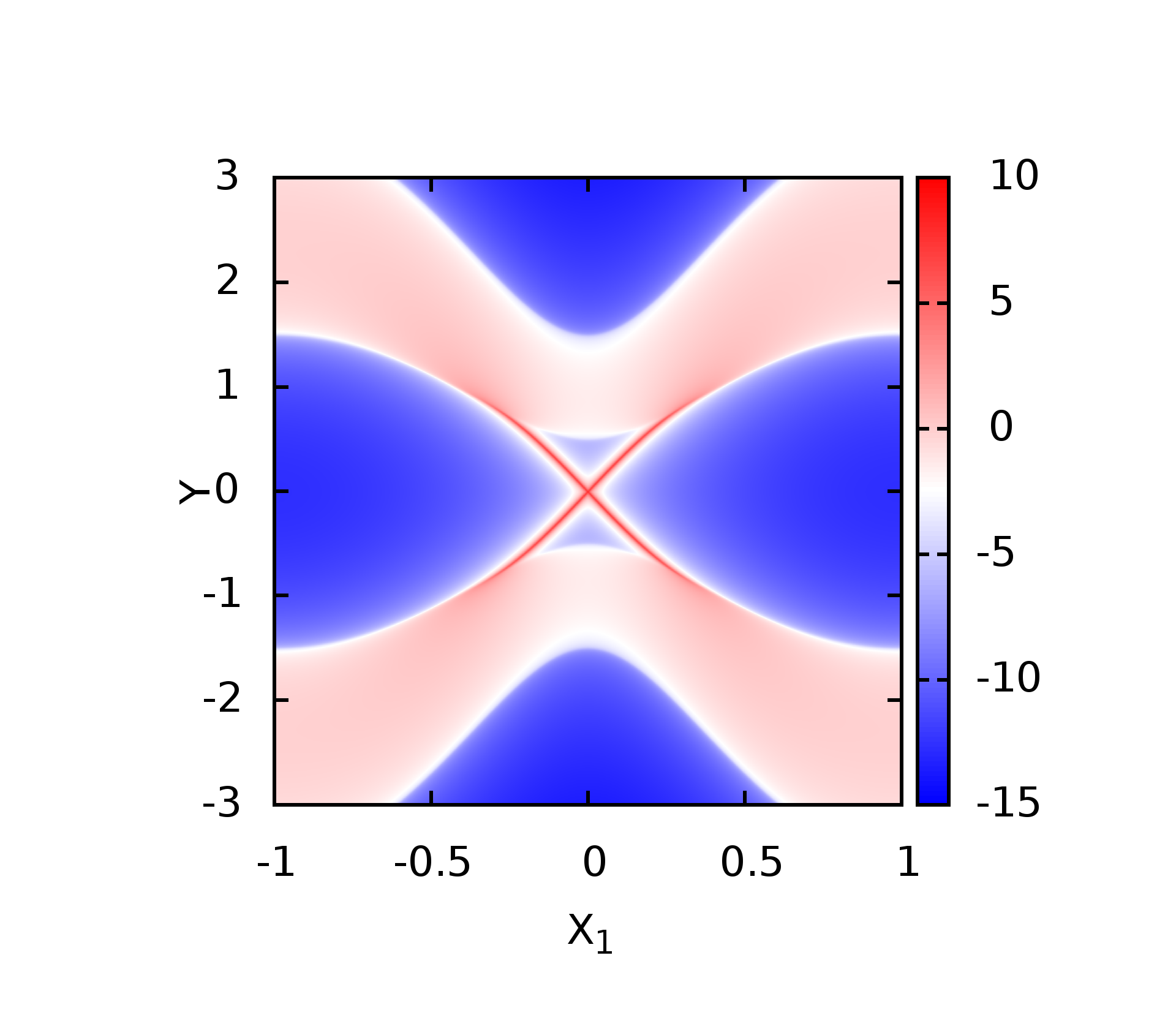
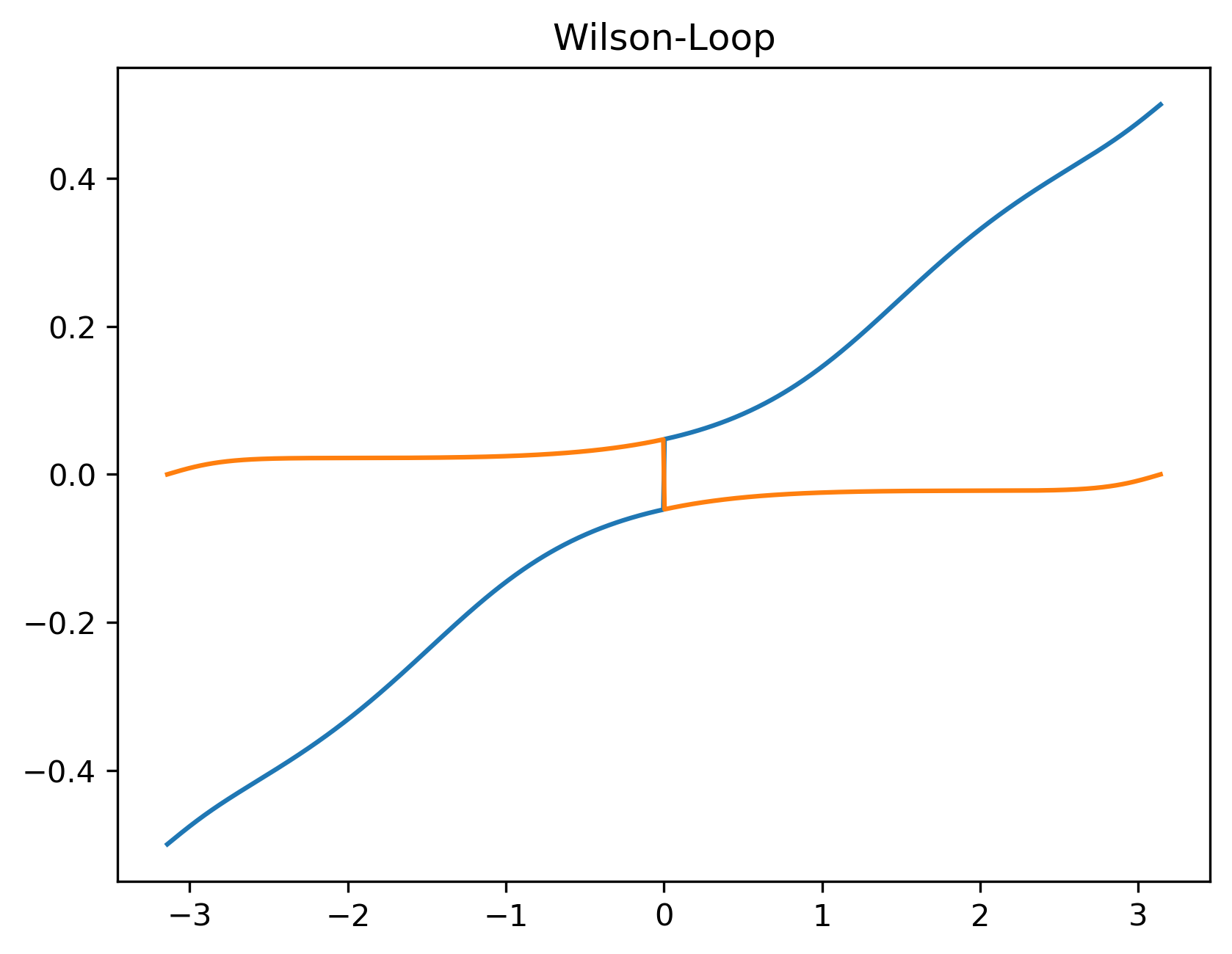
Wilson Loop计算
打卡11月的第一个任务,在前面的博客中提到过计算拓扑不变量的问题,利用Wilson Loop的方法可以很好的将规范选择问题避免,最近正好在看一篇高阶拓扑半金属的文章,正好学习一下如何利用Wilson loop来计算拓扑不变量.
{:.info}
前言
在这里就不阐述到底如何计算Wilson loop,它与Wannier Center的关系可以看我的这篇博客通过Wannier Center计算体系Z2拓扑不变量,我所有的内容也是从Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection中学习的,感兴趣可以参考这篇文章,你也可以将哈密顿量换成BHZ模型,遮掩过就可以计算文章中的结果.
我这里势利用了Higher-Order Weyl Semimetals中的哈密顿量,因为自己正在看这篇文章,正好也可以学习一下如何计算Wilson loop.
代码实现
1 | using LinearAlgebra,PyPlot,DelimitedFiles |
参考
- 1.Berry Phases in Electronic Structure Theory
- 2.Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection
- 3.Higher-Order Weyl Semimetals
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。
{:.info}

|
yxliphy@gmail.com |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Yu-Xuan's Blog!
评论