打卡11月完成的第二个小任务,仔细研读了汪忠老师这篇Edge States and Topological Invariants of Non-Hermitian Systems文章,将基本内容都重复了一下,最主要的是学习计算了一下非厄SSH模型的拓扑不变量.
前言
非厄密是最近关注度比较高的一个领域,自己最近正好有空,想自己寻找一个合适的方向进一步学习.老实讲虽然现在的导师是做超导的,但是我这两年主要的关注点都在拓扑上面,其实对超导的很多内容也不是很清楚,所以就想反正拓扑掌握的比较多,干脆就在学习学习非厄密中的拓扑,我对这个方向还是非常有兴趣的,觉得它的理论看起来会更漂亮一些.
Non-Hermitian Winding number
我就不重复文章的内容了,这里主要整理一下自己在计算时候遇到的一些问题,因为之前一直在做的是厄密问题,所以在算非厄密的时候多多少少有一些坑,不过我都踩过了.
\[H(\beta) = (t_1 + \frac{\gamma}{2}+\beta t_2)\sigma_{-} + (t_1 + \frac{\gamma}{2}+\beta^{-1}t_2)\sigma_{+}\]非厄密与厄密最大的区别就在于这个时候的变量(只从函数的角度看)是$\beta$不再是$k$,所以本征态不再是Bloch形式的拓展态,会变成随着深入体系存在局域在边界上的态,也就是非厄密趋肤效应.我这里就是班门弄斧而已,想搞懂这个问题,还请移步文章.这个时候的$\beta$和原来的$k$之间也会存在着变换关系$\beta=re^{ik}$,由这个$\beta$所确定的就是广义布里渊区(GBZ).所以在计算的时候,也一定是参照这个GBZ进行的.
\[H(\beta)|u_R\rangle=E(\beta)|u_R\rangle,\quad H^\dagger(\beta)|u_L\rangle=E^*(\beta)|u_L\rangle\]在非厄密的时候是存在两种基矢的,分别为左矢$\vert u_L\rangle$和右矢$\vert u_R\rangle$.
在对$H(\beta)$进行对角化的时候可以表示为$H(\beta)=TJT^{-1}$,$J$是对角的,每个元素就是本征值,T则是每个本征值所对应的本征矢量
这里特别要注意T中的结果是$H(\beta)$的右矢,而$T^{-1\dagger}$中的则是左矢.所以通常如果使用程序计算矩阵$H(\beta)$的本征矢量和本征值之后,其实你的到的是$T$,所以可以通过求逆后再进行厄密共轭然后得到对应的左矢.这是和厄密情况完全不同的,因为厄密情况下$T$和$T^{-1\dagger}$都是幺正矩阵,它们两个是完全相同的,所以在厄密问题中,我从来没有注意过,页没出现这个情况,在非厄米的时候一定要注意.
\[Q(\beta)=|\tilde{u}_R(\beta)\rangle\langle\tilde{u}_L(\beta)|-|u_R(\beta)\rangle\langle u_L(\beta)|\]这里$\tilde{u_R}=\sigma_z\rvert u_R\rangle$,最后得到的$Q$是off-diagonal的形式
\[Q= \begin{pmatrix}0 & q\\ q^{-1}&0\end{pmatrix}\]这里就可以计算非厄密的winding number了
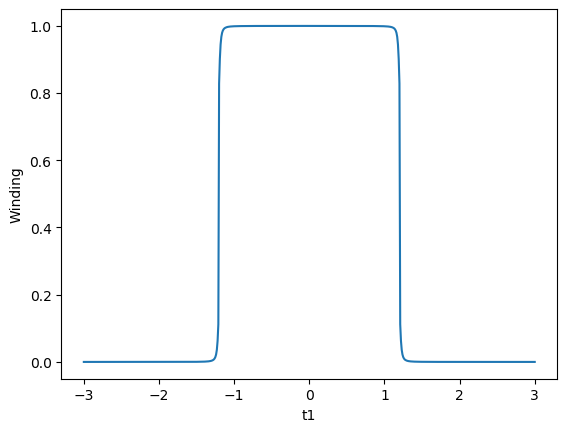
\[W = \frac{i}{2\pi}\int_{C_{\beta}}q^{-1}dq\label{wind}\]这里在进行数值计算的时候又有坑,(\ref{wind})中的$q^{-1}$就是矩阵$Q$中的$q^{-1}$,公式中的$dq$在数值求和的时候,就是相邻两个点上计算得到的$Q$中的$q$的差值,这样最后就可以得到正确的结果.
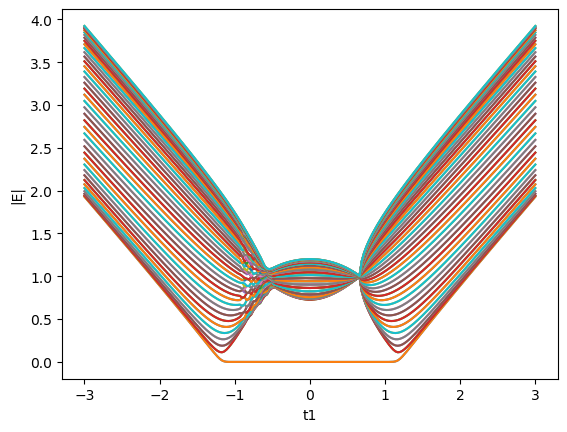
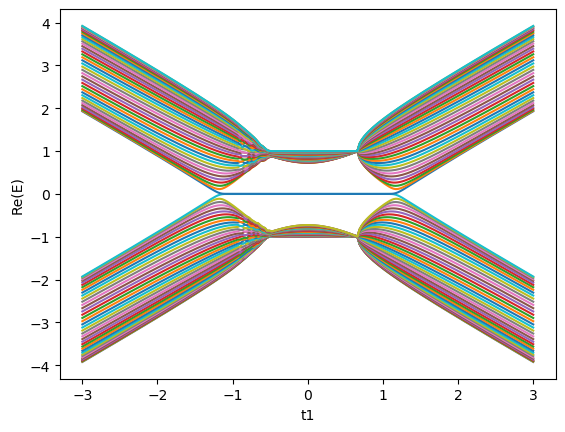
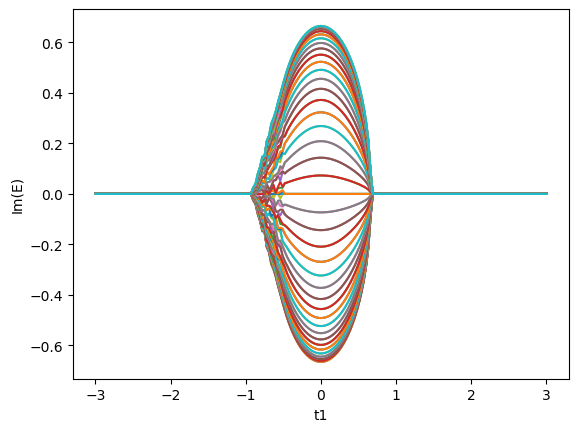
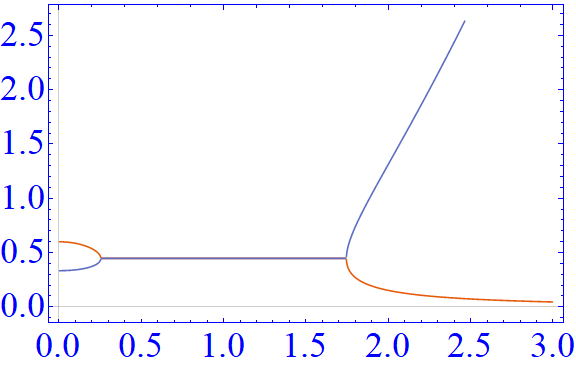
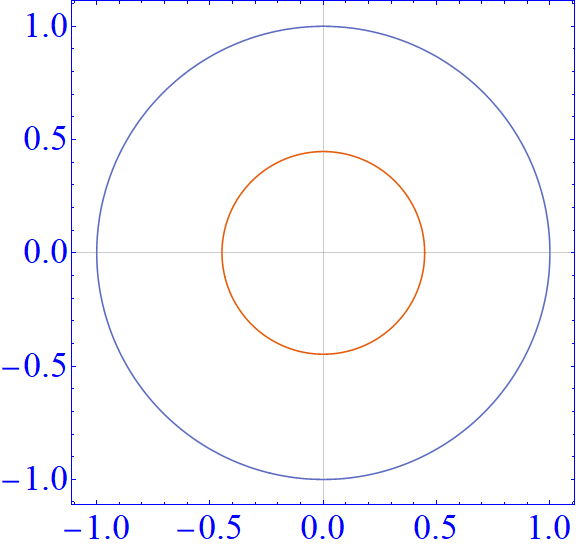
还有一些其它的结果,比如在$k$时候计算得到的开边界能谱以及非厄密趋肤效应的波函数分布,还有文章中的其它几个图,都进行了重复
代码
能带计算
# Import package which is necessary
#import Pkg
#Pkg.add("LinearAlgebra")
#Pkg.add("BenchmarkTools")
#Pkg.add("PyPlot")
using LinearAlgebra,PyPlot,DelimitedFiles
# =========================================================
#--------------------------------
function matrixSet(xn::Int64,t1::Float64,t2::Float64,t3::Float64,gam::Float64)
ham = zeros(ComplexF64,xn*2,xn*2)
#----------------------------
sigx = zeros(Float64,2,2)
sigx[1,2] = 1.0
sigx[2,1] = 1.0
sigy = zeros(ComplexF64,2,2)
sigy[1,2] = -1im
sigy[2,1] = 1im
#-----------------------------
for k in 0:xn-1
if k == 0 # First line
for m1 in 1:2
for m2 in 1:2
ham[m1,m2] = t1*sigx[m1,m2] + 1im*gam/2.0*sigy[m1,m2]
ham[m1,m2 + 2] = (t2 + t3)/2.0*sigx[m1,m2] - 1im*(t2 - t3)/2.0*sigy[m1,m2]
end
end
elseif k == xn-1
for m1 in 1:2
for m2 in 1:2
ham[k*2 + m1,k*2 + m2] = t1*sigx[m1,m2] + 1im*gam/2.0*sigy[m1,m2]
ham[k*2 + m1,k*2 + m2 - 2] = (t2 + t3)/2.0*sigx[m1,m2] + 1im*(t2 - t3)/2.0*sigy[m1,m2]
end
end
else
for m1 in 1:2
for m2 in 1:2
ham[k*2 + m1,k*2 + m2] = t1*sigx[m1,m2] + 1im*gam/2.0*sigy[m1,m2]
# right hopping
ham[k*2 + m1,k*2 + m2 + 2] = (t2 + t3)/2.0*sigx[m1,m2] - 1im*(t2 - t3)/2.0*sigy[m1,m2]
# left hopping
ham[k*2 + m1,k*2 + m2 - 2] = (t2 + t3)/2.0*sigx[m1,m2] + 1im*(t2 - t3)/2.0*sigy[m1,m2]
end
end
end
end
#----------------------------
return ham
end
# ======================================================================
function eigHam(k::Float64)
t1 = 1.0 + 0im
t2 = 1.0 + 0im
t3 = 0
gam = 1.0
#-------------------
dx = t1 + (t2 + t3)*cos(k)
dy = (t2 - t3)*sin(k)
return sqrt(dx^2 + (dy + 1im*gam/2.0)^2)
end
# ========================================================================
function edgeBand(xn::Int64)
en::Int64 = 100;
valSet = zeros(ComplexF64,2*en + 1,xn*2)
valSetre = zeros(ComplexF64,2*en + 1,xn*2)
valSetim = zeros(ComplexF64,2*en + 1,xn*2)
tlist = []
for m1 in -en:en
t1 = -3.0*m1/en
append!(tlist,t1)
ham = matrixSet(xn,t1,1.0,0.0,4.0/3.0)
val = eigvals(ham)
repart = map(real,val)
impart = map(imag,val)
val = map(abs,val)
sort!(val)
sort!(repart)
sort!(impart)
valSetre[m1 + en + 1,:] = repart
valSetim[m1 + en + 1,:] = impart
valSet[m1 + en + 1,:] = val
end
PyPlot.figure()
PyPlot.plot(tlist,valSet)
xlabel("t1")
ylabel("|E|")
savefig("absE.png",bbox_inches="tight")
PyPlot.figure()
PyPlot.plot(tlist,valSetre)
xlabel("t1")
ylabel("Re(E)")
savefig("ReE.png",bbox_inches="tight")
PyPlot.figure()
PyPlot.plot(tlist,valSetim)
xlabel("t1")
ylabel("Im(E)")
savefig("ImE.png",bbox_inches="tight")
PyPlot.show()
end
# ======================================================================
function wave(xn::Int64)
ham = matrixSet(xn,1.0,1.0,0.0,4.0/4.0)
PyPlot.figure()
val,vec = eigen(ham)
PyPlot.plot(1:xn,map(abs,vec[1:xn,:]))
PyPlot.show()
end
# =======================================================================
function main()
edgeBand(40)
wave(40)
end
# ========================================================================
main()
Winding number计算
function pauli()
# 构建Pauli矩阵
sigx = zeros(Float64,2,2)
sigy = zeros(ComplexF64,2,2)
sigz = zeros(Float64,2,2)
sigm = zeros(ComplexF64,2,2)
sigp = zeros(ComplexF64,2,2)
#----
sigx[1,2] = 1.0
sigx[2,1] = 1.0
#----
sigy[1,2] = -1im
sigy[2,1] = 1im
#----
sigz[1,1] = 1
sigz[2,2] = -1
#----
sigm = (sigx - 1im*sigy)/2.0
sigp = (sigx + 1im*sigy)/2.0
return sigp,sigm
end
# =========================================================
function hamset(k::Number,tv::Float64)::Matrix{ComplexF64}
# 哈密顿量构建
t1::Float64 = tv
t2::Float64 = 1.0
gam::Float64 = 4.0/3.0
r::Float64 = sqrt(abs((t1 - gam/2)/(t1 + gam/2)))
sigp,sigm = pauli()
ham = zeros(ComplexF64,2,2)
ham = (t1 - gam/2.0 + r*exp(1im*k)*t2)*sigm + (t1 + gam/2.0 + 1/r*exp(-1im*k)*t2)*sigp
return ham
end
# ===========================================================
function Qmat(tt::Float64,tv::Float64)
occ::Int64 = 1
sigz = zeros(Float64,2,2)
sigz[1,1] = 1
sigz[2,2] = -1
h1 = hamset(tt,tv)
vecR = eigvecs(h1)
vecL = inv(vecR)'
q1 = vecR[:,occ]
q11 = sigz*vecR[:,occ]
q2 = vecL[:,occ]
q22 = sigz*vecL[:,occ]
Q = q11*q22' - q1*q2'
return Q
end
# ================================================================
function winding(tv::Float64)
re1::ComplexF64 = 0 + 0im
kn::Int64 = 150
qmlist = []
qlist = []
dq = []
for k in 0:kn
k = 2*pi/kn*k
Q = Qmat(k,tv)
append!(qlist,Q[1,2])
append!(qmlist,Q[2,1])
end
#--------------------------
dq = qlist[2:end] - qlist[1:end-1]
for k in 1:length(qmlist)-1
re1 += qmlist[k]*dq[k]
end
return re1*1im/(2*pi)
end
# ==================================================================
function main()
tlist = []
wlist = []
for tv in -3:0.01:3
append!(tlist,tv)
append!(wlist,winding(tv))
end
wlist = map(real,wlist)
#wlist = map(floor,wlist)
plot(tlist,wlist)
xlabel("t1")
ylabel("Winding")
savefig("TopoInv.png",bbox_inches="tight")
end
# ===============================
main()
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |