在之前的博客中Python稀疏矩阵对角化库,我虽然介绍了一个python的库,可以用来计算稀疏矩阵的一些特定要求的本征矢量和本征值,但是python通常情况下是比较慢的,幸运的是这个功能最近正好的Julia中科成功的实现了,而且用法和python中几乎相同,这里正好就拿Julia来实验一下.
前言
对于julia同样是需要安装一个库才可以Arpack
import Pkg
Pkg.add("Arpack")
安装完成之后,就可以使用了
实例(Julia)
using Arpack,LinearAlgebra,DelimitedFiles
# ====================================
function matset(xn::Int64,ky::Float64)
m0 = 1.5 # Effect mass
mu = 0 # Chemical potential
tx = 1.0
ty = 1.0
ax = 1.0
ay = 1.0
del0 = 0
delx = 0.
dely = -0.
h = 0
N = xn*8
ham = zeros(ComplexF64,N,N)
#-------------------------------------------------------------------------------
g1 = zeros(ComplexF64,8,8)
g2 = zeros(ComplexF64,8,8)
g3 = zeros(ComplexF64,8,8)
g4 = zeros(ComplexF64,8,8)
g5 = zeros(ComplexF64,8,8)
g6 = zeros(ComplexF64,8,8)
# === Matrix settinf =====
g1[1,1] = 1
g1[2,2] = -1
g1[3,3] = 1
g1[4,4] = -1
g1[5,5] = -1
g1[6,6] = 1
g1[7,7] = -1
g1[8,8] = 1
# ======
g2[1,2] = 1
g2[2,1] = 1
g2[3,4] = -1
g2[4,3] = -1
g2[5,6] = 1
g2[6,5] = 1
g2[7,8] = -1
g2[8,7] = -1
# ======
g3[1,2] = -im
g3[2,1] = im
g3[3,4] = -im
g3[4,3] = im
g3[5,6] = im
g3[6,5] = -im
g3[7,8] = im
g3[8,7] = -im
# ======
g4[1,7] = -1
g4[2,8] = -1
g4[3,5] = 1
g4[4,6] = 1
g4[7,1] = -1
g4[8,2] = -1
g4[5,3] = 1
g4[6,4] = 1
# =======
g5[1,1] = 1
g5[2,2] = 1
g5[3,3] = 1
g5[4,4] = 1
g5[5,5] = -1
g5[6,6] = -1
g5[7,7] = -1
g5[8,8] = -1
# ==============
g6[1,3] = 1
g6[2,4] = 1
g6[3,1] = 1
g6[4,2] = 1
g6[5,7] = -1
g6[6,8] = -1
g6[7,5] = -1
g6[8,6] = -1
#--------------------------------------------------------------------------------
for k in 0:xn-1
if k == 0
for m in 1:8
for l in 1:8
ham[m,l] = (m0-ty*cos(ky))*g1[m,l] + (del0+dely*cos(ky))*g4[m,l] + ay*sin(ky)*g3[m,l]+ mu*g5[m,l] + h*g6[m,l]
ham[m,l+8] = (-tx*g1[m,l] + im*ax*g2[m,l] + delx*g4[m,l])/2
end
end
elseif k == xn-1
for m = 1:8
for l = 1:8
ham[k*8 + m,k*8 + l] = (m0-ty*cos(ky))*g1[m,l] + (del0+dely*cos(ky))*g4[m,l] + ay*sin(ky)*g3[m,l]+ mu*g5[m,l] + h*g6[m,l]
ham[k*8 + m,k*8 + l - 8] = conj((-tx*g1[m,l] + im*ax*g2[m,l] + delx*g4[m,l])/2)
end
end
else
for m = 1:8
for l = 1:8
ham[8*k + m,8*k + l] = (m0 - ty*cos(ky))*g1[m,l] + (del0+dely*cos(ky))*g4[m,l] + ay*sin(ky)*g3[m,l]+ mu*g5[m,l] + h*g6[m,l]
ham[8*k + m,8*k + l + 8] = (-tx*g1[m,l] + im*ax*g2[m,l])/2 + delx/2*g4[m,l]
ham[8*k + m,8*k + l - 8] = conj((-tx*g1[m,l] + im*ax*g2[m,l])/2 + delx/2*g4[m,l])
end
end
end
end
return ham
end
# =============================================
ham = matset(1000,1.0)
ts = time()
val,vec = eigs(ham, nev = 10, which=:SM); # SM 取本征值大小最小的nev个本征值和本征矢量
tn = time()
f1 = open("time-julia.dat","w")
write(f1,"Time cost for Julia is ")
writedlm(f1,tn-ts)
close(f1)
#println(tn-ts)
实例(Fortran)
module param
implicit none
integer xn,yn,kn
parameter(xn=1000,kn=30)
integer,parameter::N=xn*8
real,parameter::pi = 3.1415926535
complex,parameter::im = (0.,1.0) !虚数单位
!========== Hamiltonian ==========
complex::H0(N,N) = 0
complex::H1(N,N) = 0
complex::H2(N,N) = 0
complex::Ham(N,N) = 0
!=================================
real m0 !Driac mass
real tx,ty
real ax,ay
real del0,delx,dely
complex::g1(8,8) = 0
complex::g2(8,8) = 0
complex::g3(8,8) = 0
complex::g4(8,8) = 0
!================MKL===============
integer::lda = N
integer,parameter::lwmax=2*N+N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork ! at least 2*N+N**2
integer lrwork ! at least 1 + 5*N +2*N**2
integer liwork ! at least 3 +5*N
integer info
end module param
!================= PROGRAM START ============================
program ex01
use param
integer m,l
real ky
real t1,t2
!====空间申请==================
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
call gamma()
!parameter value setting =====
m0 = 1.5
tx = 1.0
ty = 1.0
ax = 1.0
ay = 1.0
del0 = 0
delx = 0.5
dely = -0.5
call cpu_time(t1)
call en(1.0)
call cpu_time(t2)
open(20,file="time-fortran.dat")
write(20,*)"Time cost for Fortran is ",t2-t1
close(20)
!===== Matrix set value ======
! open(1,file='en_band.dat')
! do m=-kn,kn
! ky=pi*m/kn
! call en(ky)
! !write(1,999)ky/pi,(w(i),i=1,N)
! write(1,999)ky,(w(i),i=1,N)
! enddo
close(1)
999 format(241f11.5)
stop
end program
!========================== PROGRAM END =====================
subroutine en(ky)
use param
real ky
call matrix(ky)
call matrix_verify()
call eigSol()
end subroutine en
!======================== Pauli Matrix driect product============================
subroutine gamma()
use param
!=== Matrix settinf =====
g1(1,1) = 1
g1(2,2) = -1
g1(3,3) = 1
g1(4,4) = -1
g1(5,5) = -1
g1(6,6) = 1
g1(7,7) = -1
g1(8,8) = 1
!======
g2(1,2) = 1
g2(2,1) = 1
g2(3,4) = -1
g2(4,3) = -1
g2(5,6) = 1
g2(6,5) = 1
g2(7,8) = -1
g2(8,7) = -1
!======
g3(1,2) = -im
g3(2,1) = im
g3(3,4) = -im
g3(4,3) = im
g3(5,6) = im
g3(6,5) = -im
g3(7,8) = im
g3(8,7) = -im
!======
g4(1,7) = -1
g4(2,8) = -1
g4(3,5) = 1
g4(4,6) = 1
g4(7,1) = -1
g4(8,2) = -1
g4(5,3) = 1
g4(6,4) = 1
return
end subroutine gamma
!==========================================================
subroutine matrix(ky)
use param
real ky
integer m,l,k
Ham = 0
!========== Positive energy ========
do k = 0,xn-1
if (k == 0) then ! Only right block in first line
do m = 1,8
do l = 1,8
Ham(m,l) = (m0-ty*cos(ky))*g1(m,l) + (del0+dely*cos(ky))*g4(m,l) + ay*sin(ky)*g3(m,l)
Ham(m,l+8) = (-tx*g1(m,l) + im*ax*g2(m,l))/2 + delx/2*g4(m,l)
end do
end do
elseif ( k==xn-1 ) then ! Only left block in last line
do m = 1,8
do l = 1,8
Ham(k*8+m,k*8+l) = (m0-ty*cos(ky))*g1(m,l) + (del0+dely*cos(ky))*g4(m,l) + ay*sin(ky)*g3(m,l)
Ham(k*8+m,k*8+l-8) = conjg((-tx*g1(m,l) + im*ax*g2(m,l))/2) + conjg(delx/2*g4(m,l))
end do
end do
else
do m = 1,8
do l = 1,8 ! k start from 1,matrix block from 2th row
Ham(8*k+m,8*k+l) = (m0 - ty*cos(ky))*g1(m,l) + (del0+dely*cos(ky))*g4(m,l) + ay*sin(ky)*g3(m,l)
Ham(8*k+m,8*k+l+8) = (-tx*g1(m,l) + im*ax*g2(m,l))/2 + delx/2*g4(m,l)
Ham(8*k+m,8*k+l-8) = conjg((-tx*g1(m,l) + im*ax*g2(m,l))/2) + conjg(delx/2*g4(m,l))
end do
end do
end if
end do
return
end subroutine matrix
!============================================================
subroutine matrix_verify()
use param
integer i,j
integer ccc
ccc = 0
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(16,file = 'hermitian.dat')
ccc = ccc +1
write(16,*)i,j
write(16,*)Ham(i,j)
write(16,*)Ham(j,i)
write(16,*)"===================="
write(*,*)"Ham isn't Hermitian."
stop
end if
end do
end do
close(16)
return
end subroutine matrix_verify
!================= 矩阵本征值求解 ==============
subroutine eigSol()
use param
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file="mes.txt",status="unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
open(100,file="eigval.dat")
do m = 1,N
write(100,*)m,w(m)
end do
close(100)
return
end subroutine eigSol
实例(Python)
import numpy as np
from numba import jit
from scipy.sparse.linalg import eigs, eigsh
import time
#==========================================================
def boundary(xn,yn,zn):
# Arxiv-1909-10536
# 构建不同方向hopping的索引矩阵
nxy = xn*yn
nxyz = xn*yn*zn
bry = np.zeros((6,nxyz),dtype=int)
for iz in range(zn):
for iy in range(yn):
for ix in range(xn):
i = iz*nxy + iy*xn + ix
bry[0,i] = i + 1 # x正向hopping
if(ix==xn - 1):
bry[0,i] = bry[0,i] - xn
bry[1,i] = i - 1 # x负向hopping
if(ix==0):
bry[1,i] = bry[1,i] + xn
bry[2,i] = i + xn # y正向hopping
if(iy==yn - 1):
bry[2,i] = bry[2,i] - nxy
bry[3,i] = i - xn # y负向hopping
if(iy==0):
bry[3,i] = bry[3,i] + nxy
bry[4,i] = i + nxy # z正向hopping
if(iz==zn - 1):
bry[4,i] = bry[4,i] - nxyz
bry[5,i] = i - nxy # z负向hopping
if(iz == 0):
bry[5,i] = bry[5,i] + nxyz
return bry
#=============================================================
def phase(x,y):
chi = 1.0
return np.tanh(np.sqrt(1.0*x**2 + 1.0*y**2)/chi)*(x + 1j*y)/np.sqrt(1.0*x**2 + 1.0*y**2)
#===========================================================
def hamset(xn,yn,zn):
nxy = xn*yn
nxyz = xn*yn*zn
N = nxyz*8
m0 = -2.5
t2 = 1.0
t1z = 1.0
t1x = 1.0
t1y = 1.0
t0x = 1.0
t0y = 1.0
t0z = 1.0
del0 = 0.3
delx = 0
dely = 0
mu = 0.1
ham = np.zeros((N,N))*(1+0j)
bry = boundary(xn,yn,zn)
#-----------------------------
for iz in range(zn):
for iy in range(yn):
for ix in range(xn):
i = iz*nxy + iy*xn + ix
#(1,1)
ham[i,i] = m0 - mu
if(ix != xn - 1):
ham[i,bry[0,i]] = t0x/2.0
if(ix != 0):
ham[i,bry[1,i]] = t0x/2.0
if(iy != yn - 1):
ham[i,bry[2,i]] = t0y/2.0
if(iy != 0):
ham[i,bry[3,i]] = t0y/2.0
if(iz != zn - 1):
ham[i,bry[4,i]] = t0z/2.0
if(iz != 0):
ham[i,bry[5,i]] = t0z/2.0
#(2,2)
ham[nxyz + i,nxyz + i] = m0 - mu
if(ix != xn - 1):
ham[nxyz + i,nxyz + bry[0,i]] = t0x/2.0
if(ix != 0):
ham[nxyz + i,nxyz + bry[1,i]] = t0x/2.0
if(iy != yn - 1):
ham[nxyz + i,nxyz + bry[2,i]] = t0y/2.0
if(iy != 0):
ham[nxyz + i,nxyz + bry[3,i]] = t0y/2.0
if(iz != zn - 1):
ham[nxyz + i,nxyz + bry[4,i]] = t0z/2.0
if(iz != 0):
ham[nxyz + i,nxyz + bry[5,i]] = t0z/2.0
#(3,3)
ham[nxyz*2 + i,nxyz*2 + i] = -m0 - mu
if(ix != xn - 1):
ham[nxyz*2 + i,nxyz*2 + bry[0,i]] = -t0x/2.0
if(ix != 0):
ham[nxyz*2 + i,nxyz*2 + bry[1,i]] = -t0x/2.0
if(iy != yn - 1):
ham[nxyz*2 + i,nxyz*2 + bry[2,i]] = -t0y/2.0
if(iy != 0):
ham[nxyz*2 + i,nxyz*2 + bry[3,i]] = -t0y/2.0
if(iz != zn - 1):
ham[nxyz*2 + i,nxyz*2 + bry[4,i]] = -t0z/2.0
if(iz != 0):
ham[nxyz*2 + i,nxyz*2 + bry[5,i]] = -t0z/2.0
#(4,4)
ham[nxyz*3 + i,nxyz*3 + i] = -m0 - mu
if(ix != xn - 1):
ham[nxyz*3 + i,nxyz*3 + bry[0,i]] = -t0x/2.0
if(ix != 0):
ham[nxyz*3 + i,nxyz*3 + bry[1,i]] = -t0x/2.0
if(iy != yn - 1):
ham[nxyz*3 + i,nxyz*3 + bry[2,i]] = -t0y/2.0
if(iy != 0):
ham[nxyz*3 + i,nxyz*3 + bry[3,i]] = -t0y/2.0
if(iz != zn - 1):
ham[nxyz*3 + i,nxyz*3 + bry[4,i]] = -t0z/2.0
if(iz != 0):
ham[nxyz*3 + i,nxyz*3 + bry[5,i]] = -t0z/2.0
#(1,4)
if(ix != xn - 1):
ham[i,nxyz*3 + bry[0,i]] = -1j*t1x/2.0
if(ix != 0):
ham[i,nxyz*3 + bry[1,i]] = 1j*t1x/2.0
if(iy != yn - 1):
ham[i,nxyz*3 + bry[2,i]] = -t1y/2.0
if(iy != 0):
ham[i,nxyz*3 + bry[3,i]] = t1x/2.0
#(2,3)
if(ix != xn - 1):
ham[nxyz + i,nxyz*2 + bry[0,i]] = -1j*t1x/2.0
if(ix != 0):
ham[nxyz + i,nxyz*2 + bry[1,i]] = 1j*t1x/2.0
if(iy != yn - 1):
ham[nxyz + i,nxyz*2 + bry[2,i]] = t1y/2.0
if(iy != 0):
ham[nxyz + i,nxyz*2 + bry[3,i]] = -t1x/2.0
#(3,2)
if(ix != xn - 1):
ham[nxyz*2 + i,nxyz + bry[0,i]] = -1j*t1x/2.0
if(ix != 0):
ham[nxyz*2 + i,nxyz + bry[1,i]] = 1j*t1x/2.0
if(iy != yn - 1):
ham[nxyz*2 + i,nxyz + bry[2,i]] = -t1y/2.0
if(iy != 0):
ham[nxyz*2 + i,nxyz + bry[3,i]] = t1x/2.0
#(4,1)
if(ix != xn - 1):
ham[nxyz*3 + i,bry[0,i]] = -1j*t1x/2.0
if(ix != 0):
ham[nxyz*3 + i,bry[1,i]] = 1j*t1x/2.0
if(iy != yn - 1):
ham[nxyz*3 + i,bry[2,i]] = t1y/2.0
if(iy != 0):
ham[nxyz*3 + i,bry[3,i]] = -t1x/2.0
#(1,3)
if(iz != zn - 1):
ham[i,nxyz*2 + bry[4,i]] = t1z/(2j)
if(iz != 0):
ham[i,nxyz*2 + bry[5,i]] = -t1z/(2j)
if(ix != xn - 1):
ham[i,nxyz*2 + bry[0,i]] = -1j*t2/2.0
if(ix != 0):
ham[i,nxyz*2 + bry[1,i]] = -1j*t2/2.0
if(iy != yn - 1):
ham[i,nxyz*2 + bry[2,i]] = 1j*t2/2.0
if(iy != 0):
ham[i,nxyz*2 + bry[3,i]] = 1j*t2/2.0
#(2,4)
if(iz != zn - 1):
ham[nxyz + i,nxyz*3 + bry[4,i]] = -t1z/(2j)
if(iz != 0):
ham[nxyz + i,nxyz*3 + bry[5,i]] = t1z/(2j)
if(ix != xn - 1):
ham[nxyz + i,nxyz*3 + bry[0,i]] = -1j*t2/2.0
if(ix != 0):
ham[nxyz + i,nxyz*3 + bry[1,i]] = -1j*t2/2.0
if(iy != yn - 1):
ham[nxyz + i,nxyz*3 + bry[2,i]] = 1j*t2/2.0
if(iy != 0):
ham[nxyz + i,nxyz*3 + bry[3,i]] = 1j*t2/2.0
#(3,1)
if(iz != zn - 1):
ham[nxyz*2 + i,bry[4,i]] = t1z/(2j)
if(iz != 0):
ham[nxyz*2 + i,bry[5,i]] = -t1z/(2j)
if(ix != xn - 1):
ham[nxyz*2 + i,bry[0,i]] = 1j*t2/2.0
if(ix != 0):
ham[nxyz*2 + i,bry[1,i]] = 1j*t2/2.0
if(iy != yn - 1):
ham[nxyz*2 + i,bry[2,i]] = -1j*t2/2.0
if(iy != 0):
ham[nxyz*2 + i,bry[3,i]] = -1j*t2/2.0
#(4,2)
if(iz != zn - 1):
ham[nxyz*3 + i,nxyz + bry[4,i]] = -t1z/(2j)
if(iz != 0):
ham[nxyz*3 + i,nxyz + bry[5,i]] = t1z/(2j)
if(ix != xn - 1):
ham[nxyz*3 + i,nxyz + bry[0,i]] = 1j*t2/2.0
if(ix != 0):
ham[nxyz*3 + i,nxyz + bry[1,i]] = 1j*t2/2.0
if(iy != yn - 1):
ham[nxyz*3 + i,nxyz + bry[2,i]] = -1j*t2/2.0
if(iy != 0):
ham[nxyz*3 + i,nxyz + bry[3,i]] = -1j*t2/2.0
# ---------------------------------------------------
#i = iz*nxy + iy*xn + ix
if(iy == int(yn/2)& iz == int(zn/2)):
phi = 0.0
else:
phi = phase(iy - yn/2,iz - yn/2)
#(1,6)
ham[i,nxyz*5 + i] = -1j*del0*phi
if(ix != xn - 1):
ham[i,nxyz*5 + bry[0,i]] = -1j*delx
if(ix != 0):
ham[i,nxyz*5 + bry[1,i]] = -1j*delx
if(iy != yn - 1):
ham[i,nxyz*5 + bry[2,i]] = -1j*dely
if(ix != 0):
ham[i,nxyz*5 + bry[3,i]] = -1j*dely
#(6,1)
ham[nxyz*5 + i,i] = 1j*del0*phi
if(ix != xn - 1):
ham[nxyz*5 + i,bry[0,i]] = 1j*delx
if(ix != 0):
ham[nxyz*5 + i,bry[1,i]] = 1j*delx
if(iy != yn - 1):
ham[nxyz*5 + i,bry[2,i]] = 1j*dely
if(ix != 0):
ham[nxyz*5 + i,bry[3,i]] = 1j*dely
#(5,2)
ham[nxyz*4 + i,nxyz + i] = 1j*del0*phi
if(ix != xn - 1):
ham[nxyz*4 + i,nxyz + bry[0,i]] = 1j*delx
if(ix != 0):
ham[nxyz*4 + i,nxyz + bry[1,i]] = 1j*delx
if(iy != yn - 1):
ham[nxyz*4 + i,nxyz + bry[2,i]] = 1j*dely
if(ix != 0):
ham[nxyz*4 + i,nxyz + bry[3,i]] = 1j*dely
#(2,5)
ham[nxyz + i,nxyz*4 + i] = -1j*del0*phi
if(ix != xn - 1):
ham[nxyz + i,nxyz*4 + bry[0,i]] = -1j*delx
if(ix != 0):
ham[nxyz + i,nxyz*4 + bry[1,i]] = -1j*delx
if(iy != yn - 1):
ham[nxyz + i,nxyz*4 + bry[2,i]] = -1j*dely
if(ix != 0):
ham[nxyz + i,nxyz*4 + bry[3,i]] = -1j*dely
#(3,8)
ham[nxyz*2 + i,nxyz*7 + i] = -1j*del0*phi
if(ix != xn - 1):
ham[nxyz*2 + i,nxyz*7 + bry[0,i]] = -1j*delx
if(ix != 0):
ham[nxyz*2 + i,nxyz*7 + bry[1,i]] = -1j*delx
if(iy != yn - 1):
ham[nxyz*2 + i,nxyz*7 + bry[2,i]] = -1j*dely
if(ix != 0):
ham[nxyz*2 + i,nxyz*7 + bry[3,i]] = -1j*dely
#(8,3)
ham[nxyz*7 + i,nxyz*2 + i] = 1j*del0*phi
if(ix != xn - 1):
ham[nxyz*7 + i,nxyz*2 + bry[0,i]] = 1j*delx
if(ix != 0):
ham[nxyz*7 + i,nxyz*2 + bry[1,i]] = 1j*delx
if(iy != yn - 1):
ham[nxyz*7 + i,nxyz*2 + bry[2,i]] = 1j*dely
if(ix != 0):
ham[nxyz*7 + i,nxyz*2 + bry[3,i]] = 1j*dely
for m in range(4):
for l in range(4):
for k1 in range(nxyz):
for k2 in range(nxyz):
ham[nxyz*4 + nxyz*m + k1,nxyz*4 + nxyz*l + k2] = np.conj(ham[nxyz*4 + nxyz*l + k2,nxyz*4 + nxyz*m + k1])
return ham
#=================================================================
def test():
t1 = time.time()
ham = hamset(5,5,5)
t2 = time.time()
print("Hatset timing cost is ",t2 - t1)
t1 = time.time()
#evals_all, evecs_all = eigh(X)
#evals_large, evecs_large = eigsh(X, 3, which='LM')
evals_be, evecs_be = eigsh(ham, 4, which='SM')
t2 = time.time()
print("Time cost is(s): %s"%(t2 - t1))
#==============================================
test()
结果对比
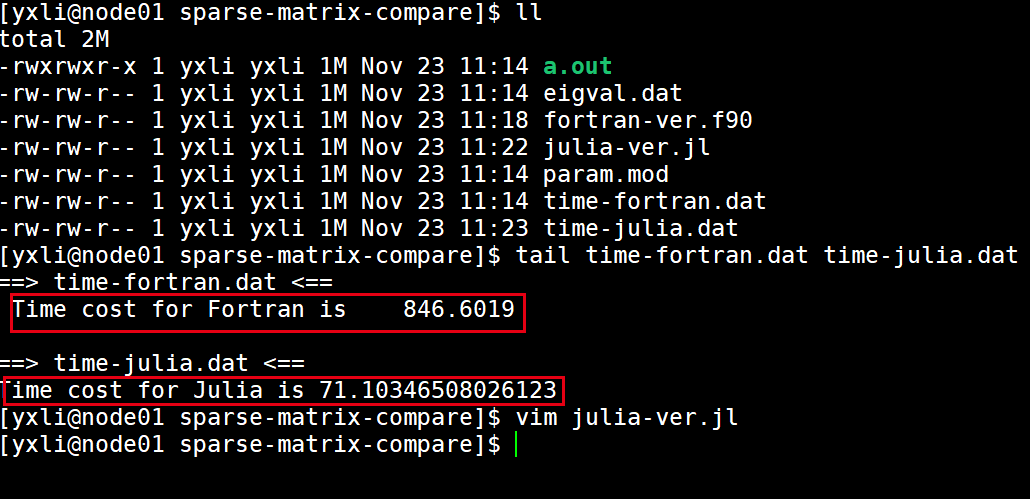
从时间对比上来看,利用Julia的效率还是比较高的.
但是这里有个问题,我在利用Fortran对角化的时候服务器的48核全部调用了,但是利用Julia的时候,仅仅调用了8核,所以从cpu用时来看是Julia快,但是真实的时间上看,还是Fortran用时短,我还没有搞清楚如何让Julia把服务器上所有的核都调用起来.
总结
通常在计算的时候,需要的也仅仅是低能或者零能附近的本征矢量和本征值,所以通过Julia的这个库函数,可以大大的缩短求解时间,而且对于维数不大的矩阵,自己的电脑也同样可以计算,对角化上相对于Fortran还是可以节省一点时间.而且从现在Julia发展的趋势来看,还是很有亲和力的,起码我觉得在矢量操作运算方面比Fortran还是方便很多的,自己现在的很多计算也都是利用Julia来进行的,我自己也放弃了好好学python的想法,因为很多python的包,在Julia的环境下也慢慢的被包括了进来.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |