这里研究一下一个square lattice,如何沿对角线方向取开边界条件,研究这种情况下的边界态是怎样的,并介绍一下如何在一个四方点阵的基础上,变成可以沿对角线开边界的模型.
前言
在通常的研究中,我经常遇到的是一个四方点阵上的紧束缚模型,这个时候想要看边界态,只需要将哈密顿量在一个方向取周期边界条件,另外一个方向取开边界条件即可.关于这种形式的问题,可以参考Chern Insulator边界态及Chern数计算这篇博客,这里主要是研究怎么对一个正方点阵上的紧束缚模型,沿对角线方向开边界.
坐标系旋转
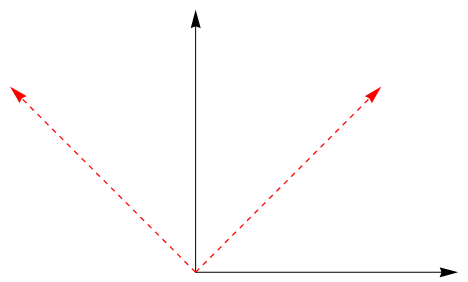
如图,黑色坐标系表示确定四方点阵的直角坐标$(k_x,k_y)$,红色虚线坐标系来确定一个旋转$45^o$后的坐标系$(k_x^{‘},k_y^{‘})$,从坐标系可以清楚的看到,对于$(k_x,k_y)$的直角坐标,其对角线方向正好就是$(k_x^{‘},k_y^{‘})$的$k_x^{‘}$方向.
所以这里最核心的思想就是将原来的直角坐标$(k_x,k_y)$旋转$45^o$变成对应的$(k_x^{‘},k_y^{‘})$坐标,在$(k_x^{‘},k_y^{‘})$的表示下沿着$k_x^{‘}$依照原来四方点阵的方法取开边界条件即可.
接下来以Chern Insulator边界态及Chern数计算这篇博客中的Chern Insulator模型来作为实例来计算,在$(k_x,k_y)$的表示下
\[H(\mathbf{k})=(m_0+t_x\cos k_x+t_y\cos k_y)\sigma_z+\lambda_x\sin k_x\sigma_x+\lambda_y\sin k_y\sigma_y\label{eq1}\]在$(k_x,k_y)$旋转$45^o$变成对应的$(k_x^{‘},k_y^{‘})$坐标的时候,它们之间的变化关系为
\[k_x^{'}=\frac{1}{\sqrt{2}}(k_x+k_y)\qquad k_y^{'}=\frac{1}{\sqrt{2}}(k_y-k_x)\]将这个关系代入之后,即可以将哈密顿量(\ref{eq1})变为
\[\begin{equation}\begin{aligned}H(\mathbf{k^{'}})&=\left[m_0+t_x(\cos \frac{1}{\sqrt{2}}k_x^{'}\cos \frac{1}{\sqrt{2}}k_y^{'}-\sin\frac{1}{\sqrt{2}}k_x^{'}\sin\frac{1}{\sqrt{2}}k_y^{'})+\\ t_y(\cos \frac{1}{\sqrt{2}}k_x^{'}\cos \frac{1}{\sqrt{2}}k_y^{'}+\sin\frac{1}{\sqrt{2}}k_x^{'}\sin\frac{1}{\sqrt{2}}k_y^{'}) \right]\sigma_z\\ &+\lambda_x(\cos\frac{1}{\sqrt{2}}k_y^{'}\sin\frac{1}{\sqrt{2}}k_x^{'}+\cos\frac{1}{\sqrt{2}}k_x^{'}\sin\frac{1}{\sqrt{2}}k_y^{'})\sigma_x\\ &+\lambda_y(\cos\frac{1}{\sqrt{2}}k_x^{'}\sin\frac{1}{\sqrt{2}}k_y^{'}-\cos\frac{1}{\sqrt{2}}k_y^{'}\sin\frac{1}{\sqrt{2}}k_x^{'})\sigma_y\end{aligned}\end{equation}\label{eq2}\]坐标旋转之后,哈密顿量又变成了关于$(k_x^{‘},k_y^{‘})$两个坐标变量的形式,这时候如果想沿$(k_x,k_y)$的对角线方向开边界,则只需要对哈密顿量(\ref{eq2})沿$k_x^{‘}$方向取开边界即可,及第一张示意图所示,剩下的问题就可Chern Insulator边界态及Chern数计算这篇博客中开边界算边界态的过程一样了.
代码
这里我线用fortran写了一下哈密顿量(\ref{eq2})的内容,然后计算了对应的边界态
! Author: YuXuanLi
! Email:yxli406@gmail.com
module pub
implicit none
integer yn,kn,hnn
parameter(yn = 50,kn = 30,hnn = 2)
integer,parameter::N = yn*hnn
real,parameter::pi = 3.1415926535
complex,parameter::im = (0.,1.0)
complex::Ham(N,N) = 0
complex g1(hnn,hnn),g2(hnn,hnn),g3(hnn,hnn)
!=================================
real m0,tx,ty,lamx,lamy
!================cheevd===============
integer::lda = N
integer,parameter::lwmax=2*N+N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork
integer lrwork
integer liwork
integer info
end module pub
!============================================================
program sol
use pub
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
!------------------------------------
m0 = 0.5
tx = 1.0
ty = 1.0
lamx = 1.0
lamy = 1.0
call main1()
stop
end program sol
!============================================================
subroutine main1()
use pub
integer m1
real k
open(3,file="openx.dat")
! open(4,file="openy-m1.dat")
do m1 = -kn,kn
k = pi*m1/kn*sqrt(2.0)
call openx(k)
write(3,999)k/pi/sqrt(2.0),(w(i),i = 1,N)
! call openy(k)
! write(4,999)k/pi,(w(i),i = 1,N)
end do
close(3)
! close(4)
999 format(201f11.6)
end subroutine main1
!============================================================
subroutine openx(ky)
use pub
real ky
call pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hnn
do l = 1,hnn
Ham(m,l) = m0*g3(m,l)
Ham(m,l + hnn) = (tx*(cos(sqrt(2.0)/2.0*ky) - 1/im*sin(sqrt(2.0)/2.0*ky)) +&
ty*(cos(sqrt(2.0)/2.0*ky) + 1/im*sin(sqrt(2.0)/2.0*ky)))*g3(m,l)+&
lamx*(1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g1(m,l)+&
lamy*(-1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g2(m,l)
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hnn
do l = 1,hnn
Ham(k*hnn + m,k*hnn + l) = m0*g3(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = (tx*(cos(sqrt(2.0)/2.0*ky) + 1/im*sin(sqrt(2.0)/2.0*ky)) +&
ty*(cos(sqrt(2.0)/2.0*ky) - 1/im*sin(sqrt(2.0)/2.0*ky)))*g3(m,l)+&
lamx*(-1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g1(m,l)+&
lamy*(1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g2(m,l)
end do
end do
else
do m = 1,hnn
do l = 1,hnn ! k start from 1,matrix block from 2th row
Ham(k*hnn + m,k*hnn + l) = m0*g3(m,l)
Ham(k*hnn + m,k*hnn + l + hnn) = (tx*(cos(sqrt(2.0)/2.0*ky) - 1/im*sin(sqrt(2.0)/2.0*ky)) +&
ty*(cos(sqrt(2.0)/2.0*ky) + 1/im*sin(sqrt(2.0)/2.0*ky)))*g3(m,l)+&
lamx*(1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g1(m,l)+&
lamy*(-1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g2(m,l)
Ham(k*hnn + m,k*hnn + l - hnn) = (tx*(cos(sqrt(2.0)/2.0*ky) + 1/im*sin(sqrt(2.0)/2.0*ky)) +&
ty*(cos(sqrt(2.0)/2.0*ky) - 1/im*sin(sqrt(2.0)/2.0*ky)))*g3(m,l)+&
lamx*(-1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g1(m,l)+&
lamy*(1/im*cos(sqrt(2.0)/2.0*ky) + sin(sqrt(2.0)/2.0*ky))*g2(m,l)
end do
end do
end if
end do
!------------------------
call isHermitian()
call eigsol()
return
end subroutine openx
!============================================================
subroutine pauli()
use pub
g1(1,2) = 1
g1(2,1) = 1
!-----------------
g2(1,2) = -im
g2(2,1) = im
!---------------
g3(1,1) = 1
g3(2,2) = -1
end subroutine pauli
!============================================================
subroutine isHermitian()
use pub
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(16,file = 'hermitian.dat')
write(16,*)i,j
write(16,*)Ham(i,j)
write(16,*)Ham(j,i)
write(16,*)"===================="
write(*,*)"Ham isn't Hermitian"
stop
end if
end do
end do
close(16)
return
end subroutine isHermitian
!================= 矩阵本征值求解 ==============
subroutine eigSol()
use pub
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file="mes.dat",status="unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine eigSol
计算结果如下图所示
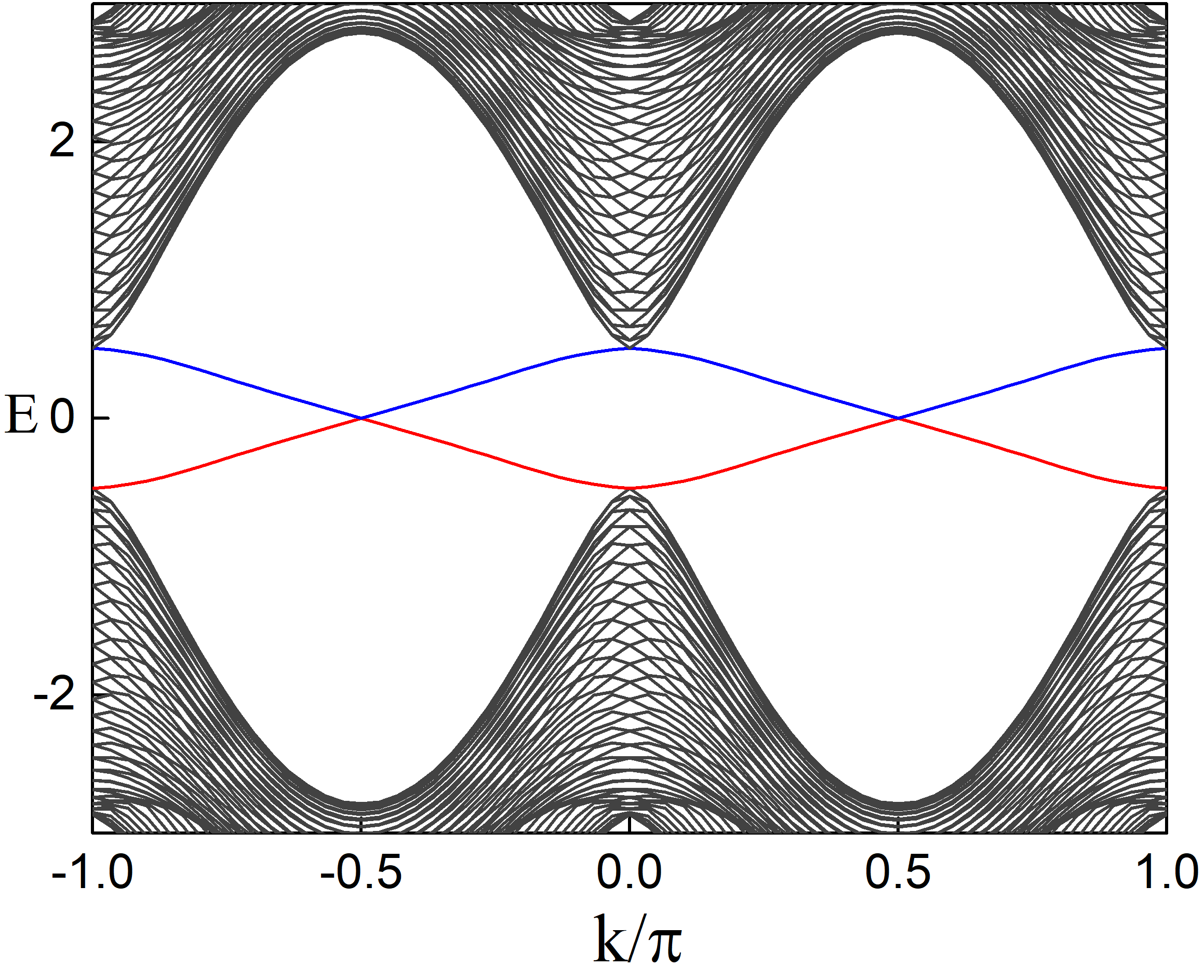
为了检验这个方法的正确性,我利用WannierTools计算Chern绝缘体性质中使用过了WannierTools,在控制参数中将开边界方向取在了对角线方向上,得到了相同的能带图.
&TB_FILE
Hrfile = "ChernInsulator_hr.dat"
/
!> bulk band structure calculation flag
&CONTROL
SlabSS_calc = T
SlabArc_calc = T
SlabBand_calc = T
JDos_calc = F
/
&SYSTEM
NumOccupied = 1 ! NumOccupied
SOC = 1 ! soc
E_FERMI = 0 ! e-fermi
/
&PARAMETERS
Eta_Arc = 0.001 ! infinite small value, like brodening
E_arc = 0.0 ! energy for calculate Fermi Arc
OmegaNum = 400 ! omega number
OmegaMin = -1.6 ! energy interval
OmegaMax = 1.6 ! energy interval
Nk1 = 201 ! number k points
Nk2 = 201 ! number k points
NP = 30 ! number of principle layers
/
LATTICE
Angstrom
1.0000000 000000000 000000000
000000000 1.0000000 000000000
000000000 000000000 1.0000000
ATOM_POSITIONS
1 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
A 0 0 0.
PROJECTORS
1 ! number of projectors
A s
SURFACE ! See doc for details
1 1 0 ! 因为是2D体系,所以第三个方向是不起作用的,(1,1)就代表的是沿对角线方向是开边界的(表面)
0 0 1
KPATH_SLAB
1 ! numker of k line for 2D case
-X -1.00 0.0 X 1.0 0.0 ! k path for 2D case
KPLANE_SLAB
-0.5 -0.5 ! Original point for 2D k plane
1.0 0.0 ! The first vector to define 2D k plane
0.0 1.0 ! The second vector to define 2D k plane for arc plots
至于计算所用的紧束缚模型的数据ChernInsulator_hr.dat,其构造方法可以查阅WannierTools计算Chern绝缘体性质这篇博客,具体数据内容如下
Chern Insulator
2
5
1 1 1 1 1
0 0 0 1 1 -0.50000000 0.00000000
0 0 0 1 2 0.00000000 0.00000000
0 0 0 2 1 0.00000000 0.00000000
0 0 0 2 2 0.50000000 0.00000000
1 0 0 1 1 0.50000000 0.00000000
1 0 0 1 2 0.00000000 -0.50000000
1 0 0 2 1 0.00000000 -0.50000000
1 0 0 2 2 -0.50000000 0.00000000
-1 0 0 1 1 0.50000000 0.00000000
-1 0 0 1 2 -0.00000000 0.50000000
-1 0 0 2 1 -0.00000000 0.50000000
-1 0 0 2 2 -0.50000000 0.00000000
0 1 0 1 1 -0.50000000 0.00000000
0 1 0 1 2 -0.50000000 -0.00000000
0 1 0 2 1 0.50000000 0.00000000
0 1 0 2 2 0.50000000 0.00000000
0 -1 0 1 1 -0.50000000 0.00000000
0 -1 0 1 2 0.50000000 0.00000000
0 -1 0 2 1 -0.50000000 -0.00000000
0 -1 0 2 2 0.50000000 0.00000000
将ChernInsulator_hr.dat与wt.in放置到相同的文件夹中,运行WannierTools即可
mpirun -np 4 wt.x wt.in &
最后会得到slabek.gnu,slabek.dat这两个文件,利用gnuplot绘图
gnuplot slabek.gnu
计算结束之后的结果如下图
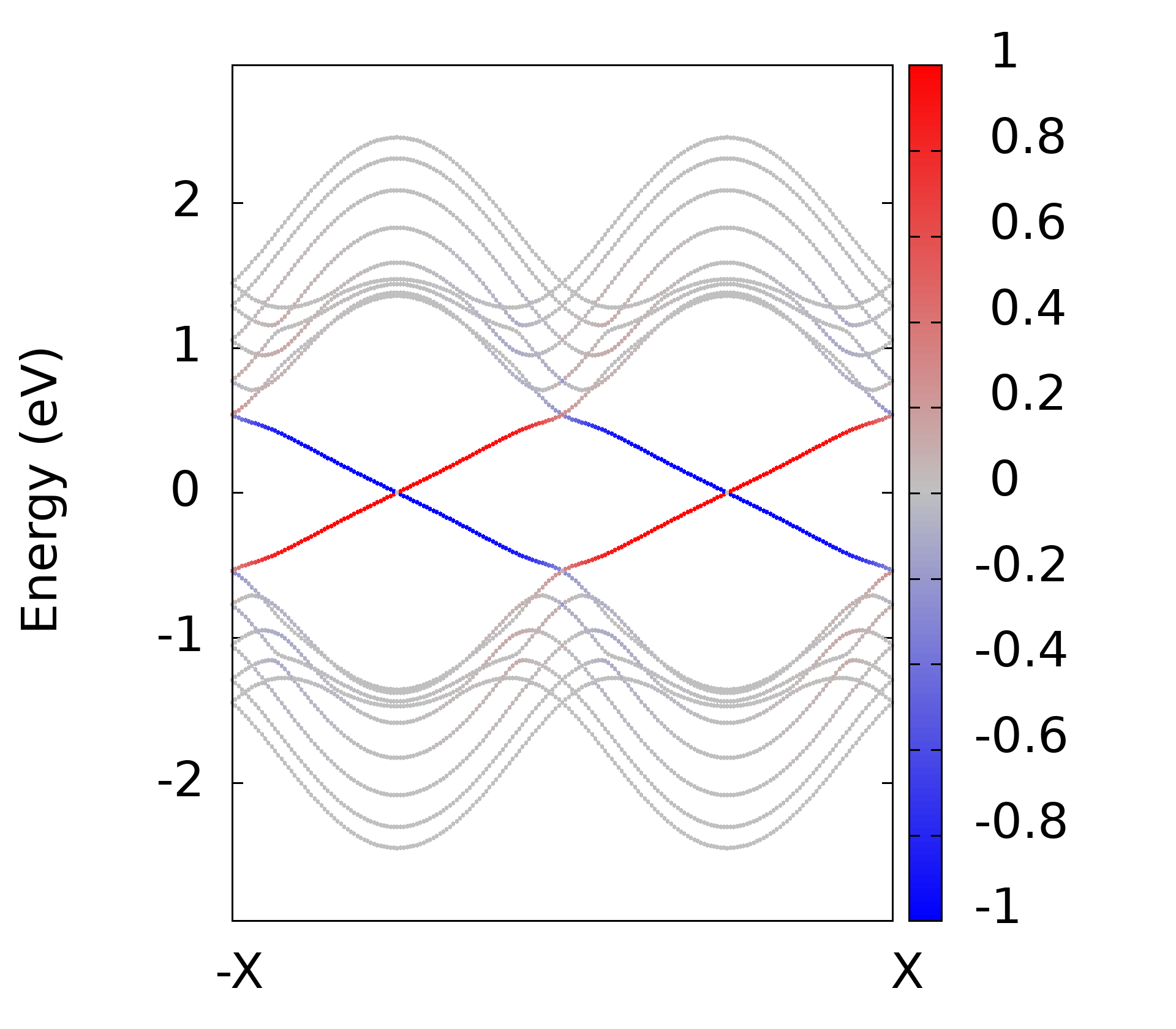
所以这里的方法是完全正确的.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |