最近在学习整理边界态理论的内容,虽然对于一般$x,y$方向开边界计算边界态在前面的博客中已经整理学习过,但是如何对任意方向开边界,并利用解析的方式来计算边界态还不是很明白,这里就整理一下自己学习这个方法的一些笔记.

前言

前面在四方点阵沿对角线方向开边界博客中主要是沿对角线方向将一个紧束缚模型做了开边界处理,但是如何从解析的角度来计算这个方向的边界态,自己并不是很清楚,在阅读文献的过程中恰好看到如何沿任意方向,利用解析的方法计算边界态,这里就整理一下自己对文章中主要解析结果的重复.这里主要的内容都是重复Helical Hinge Majorana Modes in Iron-Based Superconductors这篇文章.

边界态计算

文章的内容就不说了,直接从哈密顿量以及边界态的计算开始,首先就是拓扑铁基超导体的哈密顿量

\[\begin{equation}\begin{aligned}H(\mathbf{k})&=\left(\begin{array}{cc} H_0(\mathbf{k})-\mu&-iD(\mathbf{k})\\ iD(\mathbf{k})&\mu-H^{*}_0(\mathbf{k}) \end{array}\right)\\ H_0(\mathbf{k})&=v(\sin k_x\Gamma_1+\sin k_y\Gamma_2+\sin k_z\Gamma_3)+m(\mathbf{k})\\ m(\mathbf{k})&=m_0-m_1(\cos k_x+\cos k_y)-m_2\cos k_z \end{aligned} \end{equation}\]

$\Gamma_1=\sigma_x\otimes s_x\qquad\Gamma_2=\sigma_x\otimes s_y\qquad\sigma_x\otimes s_z\qquad\Gamma_4=\sigma_y\otimes s_0\qquad\Gamma_5=\sigma_z\otimes s_0\qquad\Gamma_{ij}=\left[\Gamma_i,\Gamma_j \right]/2i$

铁基超导配对$s_\pm$形式为$D(\mathbf{k})=\Delta(\mathbf{k})\Gamma_{13}$

\[\Delta(\mathbf{k})=\Delta_0+\Delta_1(\cos k_x+\cos k_y)\]

对于三维空间中的一个球面,可以用欧拉角来参数化,如下图所示的任意一个面$\Sigma(\phi,\theta)$

png

\[\hat{n}_{\Sigma}=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)^{T}\]

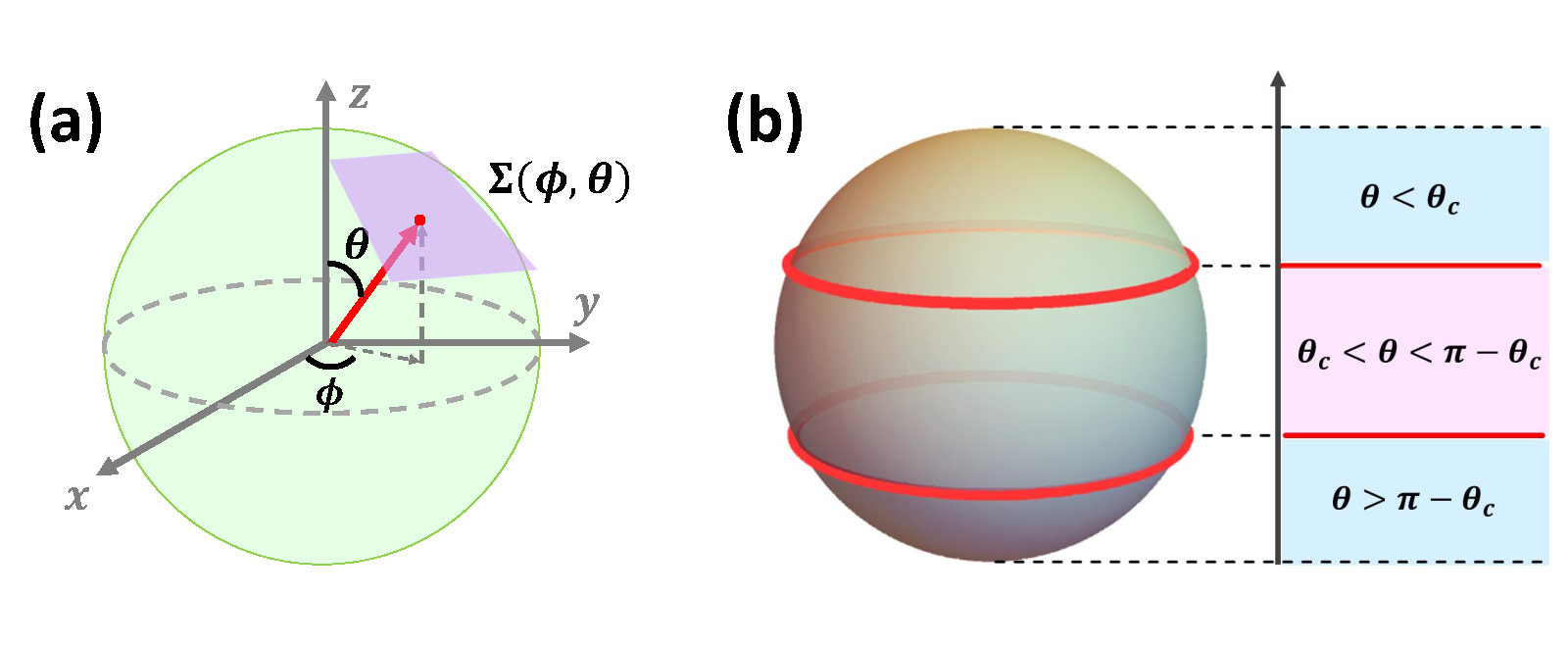
哈密顿量$H_0(\mathbf{k})$的能带反转点在$Z$,将$H_0(\mathbf{k})$在这点$(0,0,\pi)$展开

\[H_0^{Z}(\mathbf{k})=v(k_x\Gamma_1+k_y\Gamma_2-k_z\Gamma_3)+\left[\tilde{m}_0+(m_1/2)(k_x^2+k_y^2)-(m_2/2)k_z^2 \right]\Gamma_5\]

这里$\tilde{m}_0=m_0-2m_1+m_2$

要想对任意方向上的平面$\Sigma(\phi,\theta)$计有效表面理论,需要将本来的直角坐标$(k_x,k_y,k_z)$利用欧拉角代表的旋转做一个转动$R(\phi,\theta)=R_Y(-\theta)R_Z(-\phi)$

\[k^{'}=(k_1,k_2,k_3)^{T}=R(\phi,\theta)\mathbf{k}\]

通过这样的方式之后,只要确定了旋转角,就可以确定在任意角度的转动下,直角坐标基矢与转动后的坐标基矢之间的联系,然后就可以计算对应方向上的有效表面态,即在旋转坐标之后,基矢变为$(k_1,k_2,k_3)$,沿$k_3$方向取开边界条件,就可以计算$\Sigma(\phi,\theta)$面上的表面态,关于这句话的含义,还是看明白文章之后再结合文章结果来理解比较好.

在新的坐标$(k_1,k_2,k_3)$下,哈密顿量$H^Z_0({ k^{‘}})$一般具有比较复杂的形式,但是可以通过一个幺正变换,经过操作之后分解为比较简单的形式,这个幺正变换是怎么寻找的,文章中并未说明,我也没有搞清楚,这里就是借用文章中的结论.$U(\phi,\theta)=e^{i\Gamma_{13}\theta/2}e^{i\Gamma_{12}\phi/2}$

\[U(\phi,\theta)H^Z_0({ k^{'}})U(\phi,\theta)^\dagger=\tilde{h}_0+\tilde{h}_1\label{uni}\]

整个文章中,就是公式(\ref{uni})这个变化操作比较绕,因为没有给出具体计算,所以这里我就主要是通过Mathematica程序计算,来看一下每一项都是如何得出的,首先给出文章中通过分解之后得出的结果.

\[\begin{equation} \begin{aligned} \tilde{h}_0&=-vk_3\Gamma_3+(\tilde{m}_0-\tilde{m}_2k_3^2)\Gamma_5\\ \tilde{h}_1&=v(k_1\Gamma_2+k_2\Gamma_2)+(\tilde{m}_{13}k_1k_3+\tilde{m}_1k_1^2+\frac{m_1}{2}k_2^2)\Gamma_5 \end{aligned} \end{equation}\]

首先根据上面的结论确定旋转矩阵$U(\phi,\theta)$

png

下一步就是对$H^Z_0({ k^{‘}})$做幺正变换,因为是软件计算,所以变换完成之后需要做一些假设来将结果变为最简形式HTr

png

结果中coor2就是幺正变换之后的结果,这里先验证一下$\tilde{h}_0$中$-vk_3\Gamma_3$这一项,直接从coor2中挑选$\Gamma_3$这个矩阵对应的一项出来

png

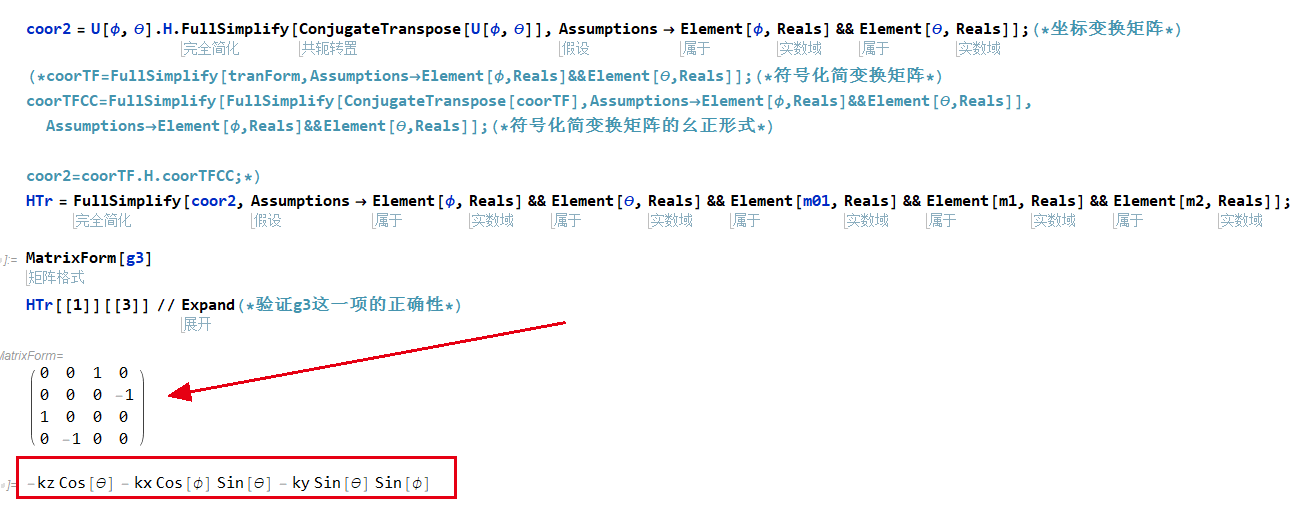
从上图中的结果中可以看到$\Gamma_3$矩阵会有(1,3)这样非零矩阵元,所以就从HTr中选取(1,3)这一项元素,结果为

\[-k_x \sin (\theta ) \cos (\phi )-k_yk_x \sin (\theta ) \sin (\phi )-k_z \cos (\theta )\label{k3}\]

坐标旋转

为了将两个不同坐标$(k_1,k_2,k_3)$与$(k_x,k_y,k_z)$联系起来,我这里先整理一下坐标上的问题.文章中提到$k_3=\hat{n}_\cdot \mathbf{k}$,所以结果为

png

所以到这一步,通过验证我们的计算结果是正确的,这里我们可以发现$\Gamma_1,\Gamma_2,\Gamma_3$它们的形式都是相似的,所以剩下的两项也是可以通过这个方式来计算的,我自己已经验证过这两项的正确性了,具体就不再这里多写了,感兴趣可以自行运算,接下来就可以利用这个程序计算分解中的其它项了.

既然已经得到了转动后$k_3$的表达式(\ref{k3}),那么我们将$k_1,k_2$也计算出来

png

通过上面的计算,就可以得到所有的$(k_1,k_2,k_3)\rightleftarrows(k_x,k_y,k_z)$之间的变换及逆变换关系,那么自然也是可以验证$k_1\Gamma_2,k_2\Gamma_2$这种对应的项.

$\Gamma_5$

这个幺正变化中,比较麻烦的是$\Gamma_5$这一项的变换,这里就来仔细的计算这一项究竟是怎么在幺正变换中改变形式的,首先从转动过后的HTr中将$\Gamma_5$这一项提取出来

png

这时候因为上面计算HTr的时候只是做了幺正操作,并没有完成坐标的变换,所以结果仍然是$(k_x,k_y,k_z)$,这里首先将其变换到$(k_1,k_2,k_3)$这个坐标系下面,上面也已经计算出了它们之间的联系

png

这里程序的主要思路就是,先计算出$(k_x,k_y,k_z)$与$(k_1,k_2,k_3)$之间是如何通过$(\theta,\phi)$联系的,然后将结果带入到$\frac{1}{2} \left(m_1 \left(k_x^2+k_y^2\right)-k_z^2 m_2\right)+\tilde{m}_{01}$中,然后通过合并同类项

先只提取$k_1^2$这一项,结果为

\[\frac{1}{4} k_1^2 (m_1\cos (2 \theta )+m_1+m_2 \cos (2 \theta )-m_2)\]

再利用三角函数关系

\[\cos (2 \theta )+1=2\cos(\theta)^2\qquad 1-\cos (2 \theta )=2\sin(\theta)^2\]

即可以得到$k_1^2$前面的系数为

\[\tilde{m}_1=(m_2\cos^2(\theta)-m_1\sin^2(\theta))/2\]

提取$k_1k_3$前面的系数$\frac{1}{4}k_1k_3 (2m_1 \sin (2 \theta )+2m_2 \sin (2 \theta ))$

\[\frac{1}{4}(2m_1 \sin (2 \theta )+2m_2 \sin (2 \theta ))=(m_1+m_2)\sin(2\theta)/2=\tilde{m}_{13}\]

提取$k_2^2$前面的系数

\[\frac{m_1}{2}\]

$\tilde{m}_0$不随幺正变换改变

\[\tilde{m}_0=m_0-2m_1+m_2\]

png

到这里通过幺正变换分解哈密顿量的操作就全部完成了,文章中剩下的部分就是求解边界态的微分方程.

微分方程求解

将方程通过幺正变换分解为这个形式之后,求解有效边界理论即为先求解$\tilde{h}_0$的零能本本征解,然后将$\tilde{h}_1$当作微扰来计算,而这个求解过程,在前面的两篇博客有效边界理论(space部分),有效边界理论(spinor部分)中已经详细记录过,这篇文章中设下的内容也就完全可以求解了.如果想详细了解关于微分方程求解有效边界理论的内容,可以阅读Majorana Corner Modes in a High-Temperature Platform这篇文章,其中有详细的推导过程.

完整求解过程

首先在低能附近的哈密顿量为

\[H(\mathbf{k})=v(k_x\Gamma_1+k_y\Gamma_2-k_z\Gamma_3)+[\tilde{m}_0+m_1/2(k_x^2+k_y^2)-m_2/2k_z^2]\Gamma_5\]

在这里，因为是想求解任意方向上的边界态，所以就通过转动坐标系的方式来得到一个任意的表面$\Sigma(\phi,\theta)$，方法是利用欧拉转动$R(\theta,\phi)=R_y(-\theta)R_z(-\phi)$，这里的关键问题就是如何将这个转动作用到哈密顿量上，首先来看这个操作，第一步是绕着$Y$轴转动一个角度$-\theta$，接下来再绕着$Z$轴转动一个角度$-\phi$，这里的哈密顿量是以Pauli矩阵的形式表示出来的，所以就是来寻找一个幺正操作$U(\theta,\phi)$来执行这个操作，这个哈密顿量中包含了真自旋，所以在考虑转动的时候，需要考虑其对自旋的影响。

绕$Y$轴转动
\[R_y(-\theta)=e^{-i\frac{\theta}{2}\sigma_0\otimes s_y},\quad\Gamma_{13}=-\sigma_0\otimes s_y\]
这里的$s_y$就是真自旋对应的pauli矩阵，这里还有轨道自由度，它并不会随着转动发生变化，所以就是一个单位矩阵$\sigma_0$。而文章中则是利用$\Gamma_{13}$矩阵表示了出来，通过计算可以发现这两者就是相同的东西，只不过为了符号统一所以就采用了李代数中的矩阵对易关系。在这里两者之间回相差一个负号，这就是一个正方向选择的问题，是顺时针为正，还是逆时针为正方向，并不会影响结果，这个我会在后面的代码计算中给出证明。
绕$Z$轴转动
\[R_Z(\phi)=e^{-i\frac{\phi}{2}\sigma_0\otimes s_z},\quad\Gamma_{12}=\sigma_0\otimes s_z\]
这里的分析和上面的完全相同，只不过此时$\Gamma$矩阵和直接利用spin转动得到的矩阵是相同的。

分别得到了两步旋转的操作矩阵，那么就可以得到完整的幺正变换矩阵

\[U(\phi,\theta)=e^{i\Gamma_{13}\theta/2}e^{i\Gamma_{12}\phi/2}\]

将这个幺正操作作用到哈密顿量的矩阵部分之后

\[U(\phi,\theta)\Gamma_iU(\phi,\theta)=\tilde{\Gamma}_i\]

之后就可以得到关于$(\theta,\phi)$的Pauli矩阵$\tilde{\Gamma}_i$了，代入直角坐标的参量

\[k_x\tilde{\Gamma}_1+k_y\tilde{\Gamma}_x-k_z\tilde{\Gamma}_3=k_1\Gamma_1+k_2\Gamma_2-k_3\Gamma_3\]

最终将坐标变换到$(k_1,k_2,k_3)$的形式，但是矩阵部分仍然要求是$\Gamma_i$，左右两边比对之后，就可以得到$(k_1,k_2,k_3)$与直角坐标$(k_x,k_y,k_z)$之间的关系

\[k_1=k_x \cos (\theta ) \cos (\phi )+k_y \cos (\theta ) \sin (\phi )-k_z \sin (\theta )\] \[k_2 =-k_x \sin\phi + k_y\cos\phi\] \[k_3=k_x \sin (\theta ) \cos (\phi )+k_y \sin (\theta ) \sin (\phi )+k_z \cos (\theta )\]

当得到了这些关系之后，反解同样可以得到$(k_x,k_y,k_z)$关于$(k_1,k_2,k_3)$的表示形式，就可以将哈密顿量中的$\Gamma_5$这一项对应的变换后的形式，这部分内容我也都记录在了代码中。

png