这里是利用边界格林函数方法来计算边界态,相比于通常取cylinder的方法,计算速度上是要快一些,做出来的图可以更加清晰的反映边界态的特征. 在之前的Hamiltonian构建时的基矢选择这篇博客中,虽然是和哈密顿量基矢选择有关的问题,但是我同样展示了如何通过一个紧束缚哈密顿量来计算拓扑边界态,虽然这个方法也很常见,用的也比较多,但是有时候为了反映一些局部的特征,可能需要把开边界的格点数目取的非常大,这就会使的计算量变得很大,耗时较长,这里就想利用边界格林函数的方法来计算边界态,它的优点是此时需要的矩阵维度是很小的,主要就是进行迭代计算,如果所需要的精度合适,计算速度上的提升是非常客观的,而且可以将边界态的某些细节反映的非常好,这里就整理一下如何利用边界格林函数来计算这样的边界态.
模型方法
这里选用BHZ模型
\[H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+\lambda_x\sin k_x\sigma_xs_z+\lambda_y\sin k_y\sigma_y\label{ham}\]计算方法如下,已经知道了$H$之后,系统的格林函数可以写作
\[G^{-1}(z)=z-H=\left(\begin{array}{cccc} z-H_0&C&0&0\\ C^\dagger&z-H_0&C&0\\ 0&C^\dagger&z-H_0&C\\ 0&0&C^\dagger&\cdots \end{array}\right)\label{gf}\]where the diagonal block H0 describes the Hamiltonian within the same “principal layer,”这一项其实就是哈密顿量(\ref{ham})沿某一方向开边界之后,包含好量子数$k_i$的那部分,自然$C,C^\dagger$就是相邻格点之间的hopping项了,从这里就可以看出,这样哈密顿量需要处理的就只是很小的一块,计算量自然很小.
我们可以发现由于(\ref{gf})是个三对角形式,所以可以将它通过迭代的方式进行求解
\[g^{(N)}_{ij}=(z-H_0-Cg^{(N-1)}C^\dagger)^{-1}_{ij}\]对于初始条件
\[g^{(0)}=(z-H_0)^{-1}\]他就是系统的边界格林函数,当选择一定的迭代精度之后,就可以求解得到最后的边界格林函数$g^{(N)}$,通过格林函数就可以计算对应的谱函数,也就可以得到边界态的结果
\[A(\omega,k_i)=-\frac{1}{\pi}\textrm{Im}(g^{(N)}(\omega,k_i))\]结果如下图
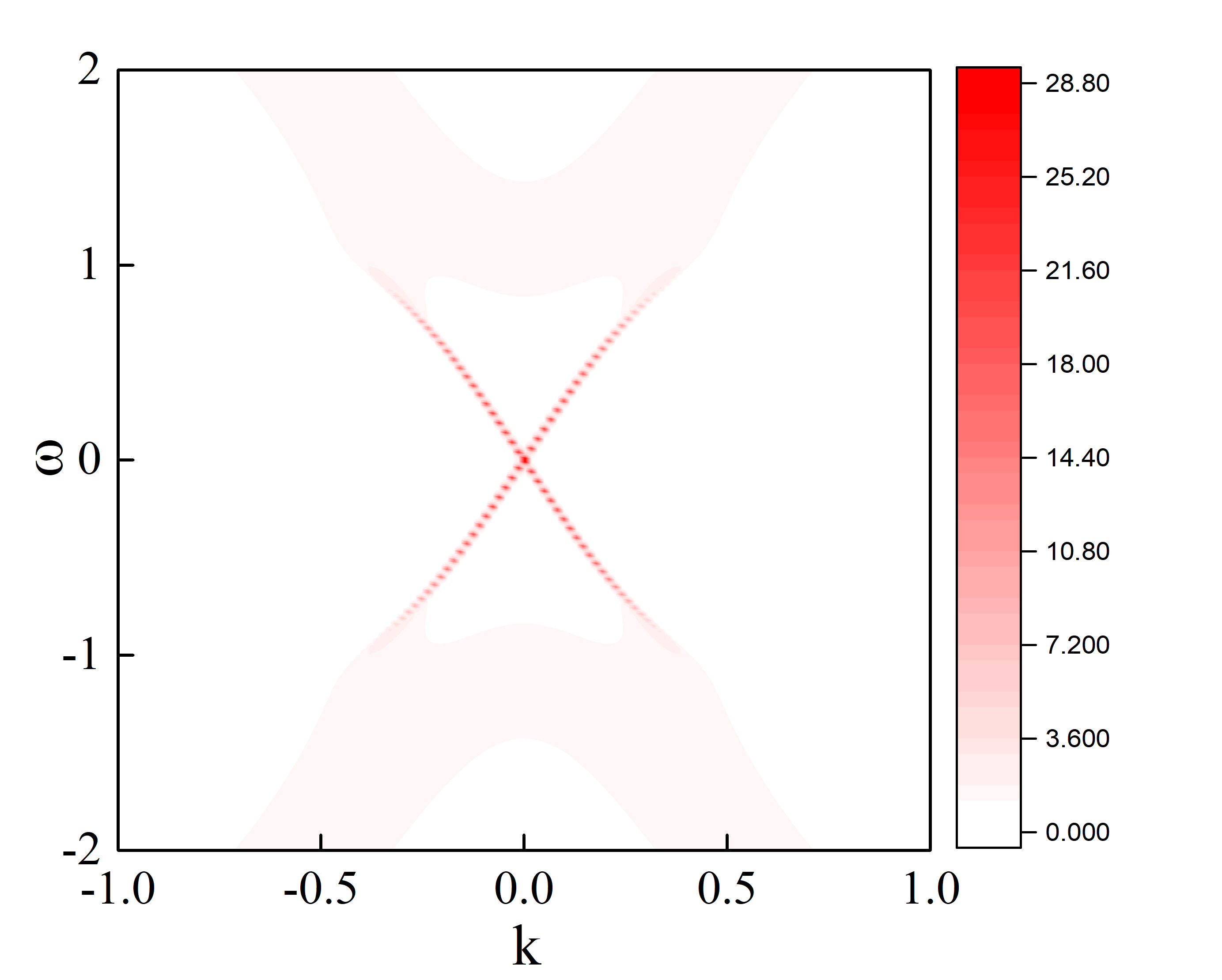
这里计算得到的图像并不是很光滑,这与计算的时候选择的计算间隔以及格林函数中的小虚部有关,而且和作图工具也有关系,不过我最近在学习利用gunplot来做图,因为是命令作图,基矢数据量非常大也不同担心电脑死机,而用类似origin的前端作图工具,当想让曲线光滑的时候,所需要的数据文件就会非常大,从而对电脑要求就会非常高,所以可以通过这些方面的改进来将这个图做得更好看.
代码
Julia
using LinearAlgebra,DelimitedFiles,PyPlot
#---------------------------------------------------
function Pauli()
hn = 4
g1 = zeros(ComplexF64,hn,hn)
g2 = zeros(ComplexF64,hn,hn)
g3 = zeros(ComplexF64,hn,hn)
#------ Kinetic energy
g1[1,1] = 1
g1[2,2] = -1
g1[3,3] = 1
g1[4,4] = -1
#-------- SOC-x
g2[1,2] = 1
g2[2,1] = 1
g2[3,4] = -1
g2[4,3] = -1
#---------- SOC-y
g3[1,2] = -1im
g3[2,1] = 1im
g3[3,4] = -1im
g3[4,3] = 1im
return g1,g2,g3
end
# ========================================================
function matset(ky::Float64)
hn::Int64 = 4
H00 = zeros(ComplexF64,4,4)
H01 = zeros(ComplexF64,4,4)
g1 = zeros(ComplexF64,4,4)
g2 = zeros(ComplexF64,4,4)
g3 = zeros(ComplexF64,4,4)
#--------------------
m0::Float64 = 1.5
tx::Float64 = -1.0
ty::Float64 = 1.0
ax::Float64 = 1.0
ay::Float64 = 1.0
g1,g2,g3 = Pauli()
#--------------------
for m in 1:hn
for l in 1:hn
H00[m,l] = (m0-ty*cos(ky))*g1[m,l] + ay*sin(ky)*g3[m,l]
H01[m,l] = (-tx*g1[m,l] - 1im*ax*g2[m,l])/2
end
end
#------
return H00,H01
end
# =====================================================
function iteration(omg::Number,ky::Float64)
hn::Int64 = 4
eps::Float64 = 1e-8
err::Float64 = 1.0
num::Int64 = 0.0
g0 = zeros(ComplexF64,hn,hn)
giter = zeros(ComplexF64,hn,hn)
gdiff = zeros(ComplexF64,hn,hn)
unit = zeros(ComplexF64,hn,hn)
h00 = zeros(ComplexF64,hn,hn)
h01 = zeros(ComplexF64,hn,hn)
h00,h01 = matset(ky)
for i in 1:hn
unit[i,i] = 1
end
g0 = inv(omg*unit - h00)
while(err > eps)
num += 1
giter = inv(omg*unit - h00 - h01*g0*transpose(conj(h01)))
gdiff = giter - g0
g0 = giter
err = abs(sum(gdiff))
end
return g0
end
# ===========================================================
function main()
hn::Int64 = 4
g0 = zeros(ComplexF64,hn,hn)
re::ComplexF64 = 0.0
eta::Float64 = 0.01
domg::Float64 = 0.01
dk::Float64 = 0.01
f1 = open("edgeState.dat","w")
for omg in -2:domg:2
for kx in -pi:dk:pi
g0 = iteration(omg + 1im*eta,kx)
re = -sum(g0)/pi
writedlm(f1,[kx/pi omg imag(re)])
end
end
close(f1)
end
# =============================================================
main()
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |