前面的一篇博客利用表面格林函数计算了边界态,虽然相比于通常对角化哈密顿量矩阵的方法要节省之间,但是迭代的收敛速度会比较慢,这里就提供一种收敛速度更快的方法来计算边界态. 在之前的利用格林函数求解边界态这篇博客中,利用边界格林函数的方法计算了边界态,但是这个算法的收敛速度会比较慢,这里就提供一个收敛速度更快的方案来计算边界态.关于这个算法的内容可以参考Highly convergent schemes for the calculation of bulk and surface Green functions这篇文章,里面有对算法详细的描述.
模型方法
这里选用BHZ模型
\[H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+\lambda_x\sin k_x\sigma_xs_z+\lambda_y\sin k_y\sigma_y\label{ham}\]至于具体的计算方法可以阅读Highly convergent schemes for the calculation of bulk and surface Green functions这篇文章。
结果如下图
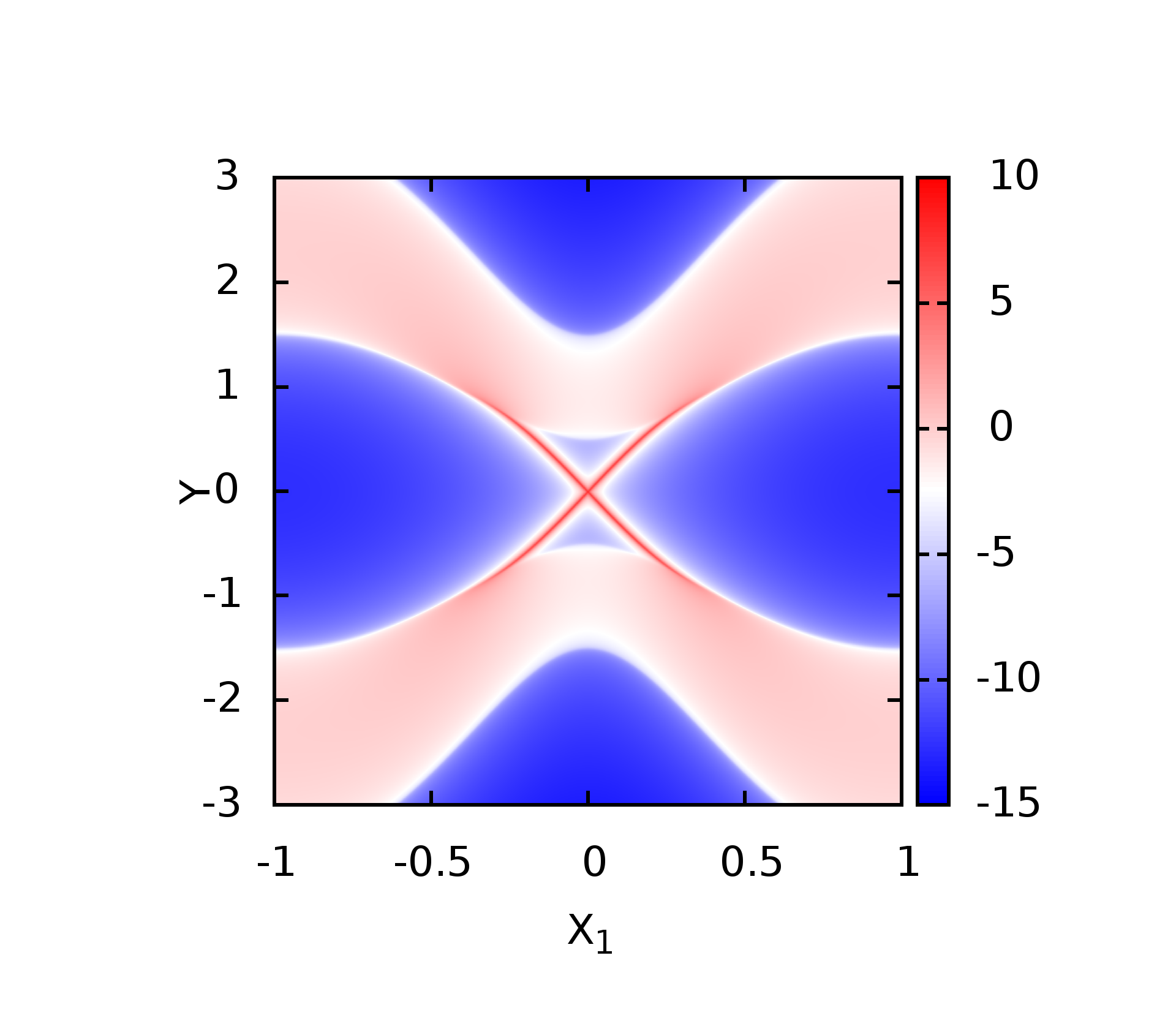
这里的结果稍稍有点问题,我自己也没有非常明白问题的来源,因为始终没有边界态的出现,而且结果与计算中$k,\omega$的选取间隔有关,与收敛的精度控制也有关系.
代码
Julia
using LinearAlgebra,DelimitedFiles,PyPlot
#---------------------------------------------------
function Pauli()
hn = 4
g1 = zeros(ComplexF64,hn,hn)
g2 = zeros(ComplexF64,hn,hn)
g3 = zeros(ComplexF64,hn,hn)
#------ Kinetic energy
g1[1,1] = 1
g1[2,2] = -1
g1[3,3] = 1
g1[4,4] = -1
#-------- SOC-x
g2[1,2] = 1
g2[2,1] = 1
g2[3,4] = -1
g2[4,3] = -1
#---------- SOC-y
g3[1,2] = -1im
g3[2,1] = 1im
g3[3,4] = -1im
g3[4,3] = 1im
return g1,g2,g3
end
# ========================================================
function matset(ky::Float64)
hn::Int64 = 4
H00 = zeros(ComplexF64,4,4)
H01 = zeros(ComplexF64,4,4)
g1 = zeros(ComplexF64,4,4)
g2 = zeros(ComplexF64,4,4)
g3 = zeros(ComplexF64,4,4)
#--------------------
m0::Float64 = 1.5
tx::Float64 = 1.0
ty::Float64 = 1.0
ax::Float64 = 1.0
ay::Float64 = 1.0
g1,g2,g3 = Pauli()
#--------------------
for m in 1:hn
for l in 1:hn
H00[m,l] = (m0-ty*cos(ky))*g1[m,l] + ay*sin(ky)*g3[m,l]
H01[m,l] = (-tx*g1[m,l] - 1im*ax*g2[m,l])/2
end
end
#------
return H00,H01
end
# ====================================================================================
function gf(omg::Float64,ky::Float64)
hn::Int64 = 4
iter::Int64 = 0
itermax::Int64 = 100
eta::Float64 = 0.01
omegac::ComplexF64 = 0.0
accuarrcy::Float64 = 1E-7
erracc::Float64 = 0.0
epsilon0 = zeros(ComplexF64,hn,hn)
epsilon0s = zeros(ComplexF64,hn,hn)
epsiloni = zeros(ComplexF64,hn,hn)
epsilonis = zeros(ComplexF64,hn,hn)
alpha0 = zeros(ComplexF64,hn,hn)
alphai = zeros(ComplexF64,hn,hn)
beta0 = zeros(ComplexF64,hn,hn)
betai = zeros(ComplexF64,hn,hn)
H00 = zeros(ComplexF64,hn,hn)
H01 = zeros(ComplexF64,hn,hn)
unit = zeros(ComplexF64,hn,hn)
GLL = zeros(ComplexF64,hn,hn)
GRR = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
#------------------------------------------
omegac = omg + 1im*eta
H00,H01 = matset(ky)
epsilon0s = H00
epsilon0 = H00
alpha0 = H01
beta0 = conj(transpose(H01))
#-------------------------------------
for i in 1:hn
unit[i,i] = 1
end
#--------------------------------------------
for iter in 1:itermax
epsilonis = epsilon0s + alpha0*inv(omegac*unit - epsilon0)*beta0
epsiloni = epsilon0 + beta0*inv(omegac*unit - epsilon0)*alpha0+alpha0*inv(omegac*unit - epsilon0)*beta0
alphai = alpha0*inv(omegac*unit - epsilon0)*alpha0
betai = beta0*inv(omegac*unit - epsilon0)*beta0
epsilon0s = epsilonis
epsilon0 = epsiloni
alpha0 = alphai
beta0 = betai
erracc = abs(sum(alphai))
# if erracc < accuarrcy
# break
# end
end
# GLL = inv(omegac*unit - epsilon0s)
# GBulk = inv(omegac*unit - epsilon0)
GLL = epsilon0s
GBulk = epsilon0
return GLL,GBulk
end
# ====================================================================================
function gf2(omg::Float64,ky::Float64)
hn::Int64 = 4
iter::Int64 = 0
itermax::Int64 = 100
eta::Float64 = 0.01
omegac::ComplexF64 = 0.0
epsilon0 = zeros(ComplexF64,hn,hn)
epsilon0s = zeros(ComplexF64,hn,hn)
epsiloni = zeros(ComplexF64,hn,hn)
epsilonis = zeros(ComplexF64,hn,hn)
alpha0 = zeros(ComplexF64,hn,hn)
alphai = zeros(ComplexF64,hn,hn)
beta0 = zeros(ComplexF64,hn,hn)
betai = zeros(ComplexF64,hn,hn)
H00 = zeros(ComplexF64,hn,hn)
H01 = zeros(ComplexF64,hn,hn)
unit = zeros(ComplexF64,hn,hn)
GLL = zeros(ComplexF64,hn,hn)
GRR = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
#------------------------------------------
omegac = omg + 1im*eta
H00,H01 = matset(ky)
epsilon0s = H00
epsilon0 = H00
alpha0 = H01
beta0 = conj(transpose(H01))
#-------------------------------------
for i in 1:hn
unit[i,i] = 1
end
#--------------------------------------------
for iter in 1:itermax
epsilonis = epsilon0s + alpha0*inv(omegac*unit - epsilon0)*beta0
epsiloni = epsilon0 + alpha0*inv(omegac*unit - epsilon0)*beta0 + beta0*inv(omegac*unit - epsilon0)*alpha0
alphai = alpha0*inv(omegac*unit - epsilon0)*alpha0
betai = beta0*inv(omegac*unit - epsilon0)*beta0
epsilon0s = epsilonis
epsilon0 = epsiloni
alpha0 = alphai
beta0 = betai
erracc = abs(sum(alphai))
end
# GLL = inv(omegac*unit - epsilon0s)
# GBulk = inv(omegac*unit - epsilon0)
GLL = epsilon0s
GBulk = epsilon0
return GLL,GBulk
end
# ==========================================================
function main()
hn::Int64 = 4
kn::Int64 = 600
omgN::Int64 = kn
ky::Float64 = 0.0
omg::Float64 = 0.0
GLL = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
f1 = open("bhz.dat","w")
for i0 in -kn:kn
ky = pi*i0/kn
for i1 in -omgN:omgN
omg = i1*3.0/omgN
GLL,GBulk = gf2(omg,ky)
re1 = log(-imag(sum(GLL))/pi)
re2 = log(-imag(sum(GBulk))/pi)
writedlm(f1,[ky/pi omg re1 re2 re1 + re2],"\t")
end
writedlm(f1,"\n")
end
close(f1)
end
# =========================================================
# @time main()
main()
并行版
对于较大体系的迭代格林函数,其实计算量还是比较大的,这里给一个并行版。
using DelimitedFiles
using ProgressMeter
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles
#---------------------------------------------------
@everywhere function Pauli()
hn = 4
g1 = zeros(ComplexF64,hn,hn)
g2 = zeros(ComplexF64,hn,hn)
g3 = zeros(ComplexF64,hn,hn)
#------ Kinetic energy
g1[1,1] = 1
g1[2,2] = -1
g1[3,3] = 1
g1[4,4] = -1
#-------- SOC-x
g2[1,2] = 1
g2[2,1] = 1
g2[3,4] = -1
g2[4,3] = -1
#---------- SOC-y
g3[1,2] = -1im
g3[2,1] = 1im
g3[3,4] = -1im
g3[4,3] = 1im
return g1,g2,g3
end
# ========================================================
@everywhere function matset(ky::Float64)
hn::Int64 = 4
H00 = zeros(ComplexF64,4,4)
H01 = zeros(ComplexF64,4,4)
g1 = zeros(ComplexF64,4,4)
g2 = zeros(ComplexF64,4,4)
g3 = zeros(ComplexF64,4,4)
#--------------------
m0::Float64 = 1.5
tx::Float64 = 1.0
ty::Float64 = 1.0
ax::Float64 = 1.0
ay::Float64 = 1.0
g1,g2,g3 = Pauli()
#--------------------
for m in 1:hn
for l in 1:hn
H00[m,l] = (m0-ty*cos(ky))*g1[m,l] + ay*sin(ky)*g3[m,l]
H01[m,l] = (-tx*g1[m,l] - 1im*ax*g2[m,l])/2
end
end
#------
return H00,H01
end
# ====================================================================================
@everywhere function gf(omg::Float64,ky::Float64)
hn::Int64 = 4
iter::Int64 = 0
itermax::Int64 = 100
eta::Float64 = 0.01
omegac::ComplexF64 = 0.0
accuarrcy::Float64 = 1E-7
erracc::Float64 = 0.0
epsilon0 = zeros(ComplexF64,hn,hn)
epsilon0s = zeros(ComplexF64,hn,hn)
epsiloni = zeros(ComplexF64,hn,hn)
epsilonis = zeros(ComplexF64,hn,hn)
alpha0 = zeros(ComplexF64,hn,hn)
alphai = zeros(ComplexF64,hn,hn)
beta0 = zeros(ComplexF64,hn,hn)
betai = zeros(ComplexF64,hn,hn)
H00 = zeros(ComplexF64,hn,hn)
H01 = zeros(ComplexF64,hn,hn)
unit = zeros(ComplexF64,hn,hn)
GLL = zeros(ComplexF64,hn,hn)
GRR = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
#------------------------------------------
omegac = omg + 1im*eta
H00,H01 = matset(ky)
epsilon0s = H00
epsilon0 = H00
alpha0 = H01
beta0 = conj(transpose(H01))
#-------------------------------------
for i in 1:hn
unit[i,i] = 1
end
#--------------------------------------------
for iter in 1:itermax
epsilonis = epsilon0s + alpha0*inv(omegac*unit - epsilon0)*beta0
epsiloni = epsilon0 + beta0*inv(omegac*unit - epsilon0)*alpha0+alpha0*inv(omegac*unit - epsilon0)*beta0
alphai = alpha0*inv(omegac*unit - epsilon0)*alpha0
betai = beta0*inv(omegac*unit - epsilon0)*beta0
epsilon0s = epsilonis
epsilon0 = epsiloni
alpha0 = alphai
beta0 = betai
erracc = abs(sum(alphai))
# if erracc < accuarrcy
# break
# end
end
# GLL = inv(omegac*unit - epsilon0s)
# GBulk = inv(omegac*unit - epsilon0)
GLL = epsilon0s
GBulk = epsilon0
return GLL,GBulk
end
# ====================================================================================
@everywhere function gf2(omg::Float64,ky::Float64)
hn::Int64 = 4
iter::Int64 = 0
itermax::Int64 = 100
eta::Float64 = 0.01
omegac::ComplexF64 = 0.0
epsilon0 = zeros(ComplexF64,hn,hn)
epsilon0s = zeros(ComplexF64,hn,hn)
epsiloni = zeros(ComplexF64,hn,hn)
epsilonis = zeros(ComplexF64,hn,hn)
alpha0 = zeros(ComplexF64,hn,hn)
alphai = zeros(ComplexF64,hn,hn)
beta0 = zeros(ComplexF64,hn,hn)
betai = zeros(ComplexF64,hn,hn)
H00 = zeros(ComplexF64,hn,hn)
H01 = zeros(ComplexF64,hn,hn)
unit = zeros(ComplexF64,hn,hn)
GLL = zeros(ComplexF64,hn,hn)
GRR = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
#------------------------------------------
omegac = omg + 1im*eta
H00,H01 = matset(ky)
epsilon0s = H00
epsilon0 = H00
alpha0 = H01
beta0 = conj(transpose(H01))
#-------------------------------------
for i in 1:hn
unit[i,i] = 1
end
#--------------------------------------------
for iter in 1:itermax
epsilonis = epsilon0s + alpha0*inv(omegac*unit - epsilon0)*beta0
epsiloni = epsilon0 + alpha0*inv(omegac*unit - epsilon0)*beta0 + beta0*inv(omegac*unit - epsilon0)*alpha0
alphai = alpha0*inv(omegac*unit - epsilon0)*alpha0
betai = beta0*inv(omegac*unit - epsilon0)*beta0
epsilon0s = epsilonis
epsilon0 = epsiloni
alpha0 = alphai
beta0 = betai
erracc = abs(sum(alphai))
end
# GLL = inv(omegac*unit - epsilon0s)
# GBulk = inv(omegac*unit - epsilon0)
GLL = epsilon0s
GBulk = epsilon0
return GLL,GBulk
end
# ==========================================================
@everywhere function main()
hn::Int64 = 4
kn::Int64 = 600
omgN::Int64 = kn
ky::Float64 = 0.0
omg::Float64 = 0.0
GLL = SharedArray(zeros(ComplexF64,hn,hn))
GBulk = SharedArray(zeros(ComplexF64,hn,hn))
re1 = SharedArray(zeros(Float64,2*kn + 1,2*omgN + 1))
re2 = SharedArray(zeros(Float64,2*kn + 1,2*omgN + 1))
@sync @distributed for i0 in -kn:kn
ky = i0*pi/kn
for i1 in -omgN:omgN
omg = i1*3.0/omgN
GLL,GBulk = gf2(omg,ky)
re1[i0 + kn + 1,i1 + omgN + 1] = log(-imag(sum(GLL))/pi)
re2[i0 + kn + 1,i1 + omgN + 1] = log(-imag(sum(GBulk))/pi)
end
end
f1 = open("bhz-parallel.dat","w")
for i0 in -kn:kn
kx = i0*pi/kn
for i1 in -omgN:omgN
omg = i1*3.0/omgN
writedlm(f1,[kx/pi omg re1[i0 + kn + 1,i1 + omgN + 1] re2[i0 + kn + 1,i1 + omgN + 1] re1[i0 + kn + 1,i1 + omgN + 1] + re2[i0 + kn + 1,i1 + omgN + 1]],"\t")
end
writedlm(f1,"\n")
end
close(f1)
end
# =========================================================
@time main()
通过下面的命令来给出指定的线程数量来进行并行
julia -p 16 filename.jl
速度比较
这里对julia两种版本进行速度比较,将格点密度同样取为600 * 600串行执行的结果
3067.176742 seconds (6.12 G allocations: 4.046 TiB, 8.50% gc time)
并行后开了16个线程
403.137411 seconds (34.37 M allocations: 4.617 GiB, 0.13% gc time, 0.28% compilation time)
Fortran
module pub
implicit none
integer N,iternum,hn
real err,eta,dk,domg
parameter( hn = 4, N = hn,iternum = 200,err = 1e-16,eta = 0.01,dk = 0.01,domg = dk)
real,parameter::pi = 3.1415926535
complex,parameter::im = (0.,1.0)
complex ones(N,N),GLL(N,N),GRR(N,N),GB(N,N)
complex H00(N,N) ! diagonal elementery
complex H01(N,N) ! off-diag elementery
complex g1(hn,hn),g2(hn,hn),g3(hn,hn)
!---------------------------------------------
real m0,mu
real tx,ty
real ax,ay
end module pub
!==================================================================
program main
use pub
!======parameter value setting =====
m0 = 1.5
tx = 1.0
ty = 1.0
ax = 1.0
ay = 1.0
call surfstat()
stop
end program main
!============================================================================================
subroutine surfstat()
! surfstat calculates surface state using green's function method---J.Phys.F.Met.Phys.15(1985)851-858
! 利用已经求得的格林函数来计算对应的态密度
use pub
implicit none
real kx,omg,re1,re2,re3
real t_start,t_end
integer i1
open(20,file="dos.dat")
call cpu_time(t_start)
!------------------------------------------
do kx = -pi,pi,dk
call matset(kx)
do omg = -3,3,domg
call itera(omg,kx)
re1 = log(abs(sum(aimag(GLL))))
re2 = log(abs(sum(aimag(GRR))))
re3 = log(abs(sum(aimag(GB))))
write(20,999)kx/pi,omg,re1,re2,re3
end do
write(20,*)" "
end do
!------------------------------------------
call cpu_time(t_end)
close(20)
write(*,*)"Timing const is: ",t_end - t_start
999 format(30f16.12)
return
end subroutine surfstat
!=================================================================
subroutine itera(omega,ky)
use pub
real omega,real_temp,ky
integer iter
complex omegac
complex g0dem(N,N), g0(N,N) ! Green's Function
complex epsiloni(N,N),epsilons(N,N),epsilons_t(N,N),alphai(N,N),betai(N,N) ! 迭代过程变量
complex GLLdem(N,N),GRRdem(N,N),GBdem(N,N),mat1(N,N),mat2(N,N)
!----------------------------
call matset(ky)
epsiloni = H00
epsilons = H00
epsilons_t = H00
alphai = H01
betai = conjg(transpose(H01))
omegac = omega + eta*im
!----------------------------------
do iter = 1, iternum
g0dem = omegac*ones - epsiloni ! Green's Function
call inv(g0dem, g0)
mat1 = matmul(alphai, g0)
mat2 = matmul(betai, g0)
g0 = matmul(mat1,betai)
epsiloni = epsiloni + g0
epsilons = epsilons + g0
g0 = matmul(mat2,alphai)
epsiloni = epsiloni + g0
epsilons_t = epsilons_t + g0
g0 = matmul(mat1, alphai)
alphai = g0
g0 = matmul(mat2, betai)
betai = g0
real_temp = sum(abs(alphai))
if (real_temp .le. err)then
exit
end if
end do ! end of iteration
! calculate surface green's function
GLLdem = omegac*ones- epsilons
call inv(GLLdem, GLL)
! GLL = epsilons
GRRdem = omegac*ones- epsilons_t
call inv(GRRdem, GRR)
! GRR = epsilons_t
GBdem = omegac*ones- epsiloni
call inv(GBdem, GB)
! GB = epsiloni
end subroutine itera
!================================================================
subroutine matset(ky)
! 构建哈密顿量
use pub
real ky
integer m,l
call Pauli()
do m = 1,hn
do l = 1,hn
H00(m,l) = (m0-ty*cos(ky))*g1(m,l) + ay*sin(ky)*g3(m,l)
H01(m,l) = (-tx*g1(m,l) - im*ax*g2(m,l))/2
end do
end do
!----------------------
! 初始化单位矩阵
do ix = 1,N
ones(ix,ix) = 1.0
end do
return
end subroutine matset
!=======================矩阵求逆====================================
subroutine inv(matin,matout)
use pub
complex,intent(in) :: matin(N,N) ! N is dimension of matrix which can be readed from pub model (use pub)
complex:: matout(size(matin,1),size(matin,2))
real:: work2(size(matin,1)) ! work2 array for LAPACK
integer::ipiv(size(matin,1)) ! pivot indices
integer info ! inv solution information
! Store matin in matout to prevent it from being overwritten by LAPACK
matout = matin
! SGETRF computes an LU factorization of a general M-by-N matrix A
! using partial pivoting with row interchanges.
call CGETRF(N,N,matout,N,ipiv,info)
if (info.ne.0) stop 'Matrix is numerically singular!'
! SGETRI computes the inverse of a matrix using the LU factorization
! computed by SGETRF.
call CGETRI(N,matout,N,ipiv,work2,N,info)
if (info.ne.0) stop 'Matrix inversion failed!'
return
end subroutine inv
!======================== Pauli Matrix driect product============================
subroutine Pauli()
use pub
! TI
!------ Kinetic energy
g1(1,1) = 1
g1(2,2) = -1
g1(3,3) = 1
g1(4,4) = -1
!-------- SOC-x
g2(1,2) = 1
g2(2,1) = 1
g2(3,4) = -1
g2(4,3) = -1
!---------- SOC-y
g3(1,2) = -im
g3(2,1) = im
g3(3,4) = -im
g3(4,3) = im
return
end subroutine Pauli
绘图
set encoding iso_8859_1
#set terminal postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1680
set output 'density.png'
#set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
set size ratio 1
set view map
set xtics
set ytics
#set xlabel "K_1 (1/{\305})"
set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
set ylabel "Y"
set ylabel offset 1, 0
set colorbox
set xrange [-1:1]
set yrange [-3:3]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'openy-bhz.dat' u 1:2:3 w pm3d
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |