这里整理一下最近看拓扑分类文章时候的一些笔记.
最近在做一些工作,在阅读文献的时候有一些比较重要的工作需要仔细的阅读和理解,这里我就想把自己看拓扑分类这方面的文章时的一些理解和笔记整理一下,也可以加深自己对文章的理解.
10重分类
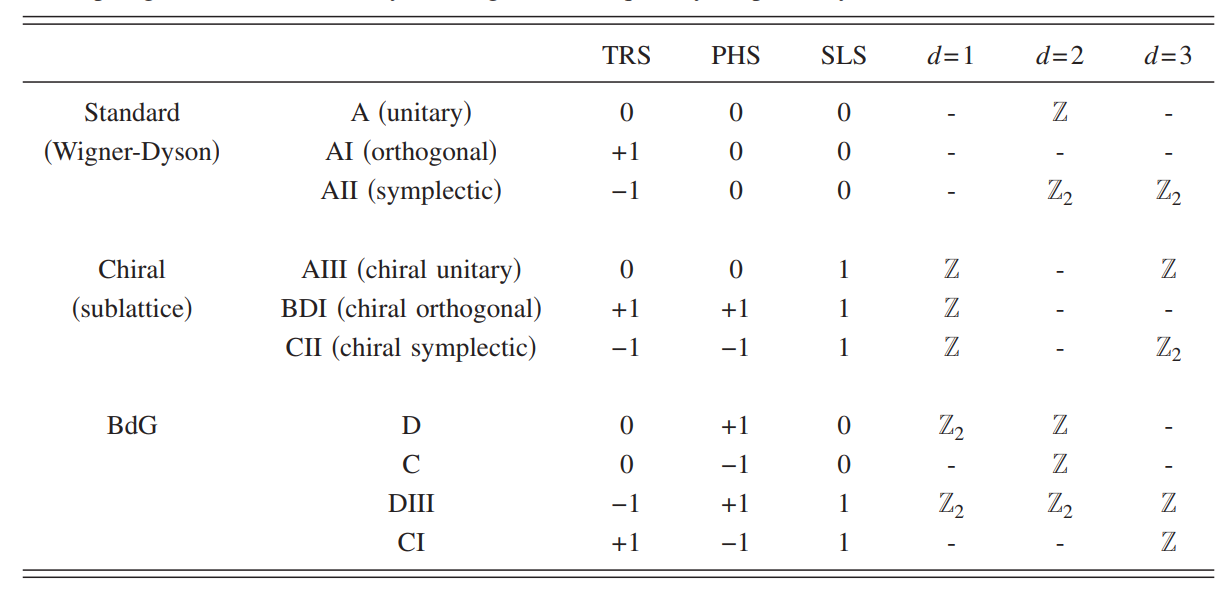
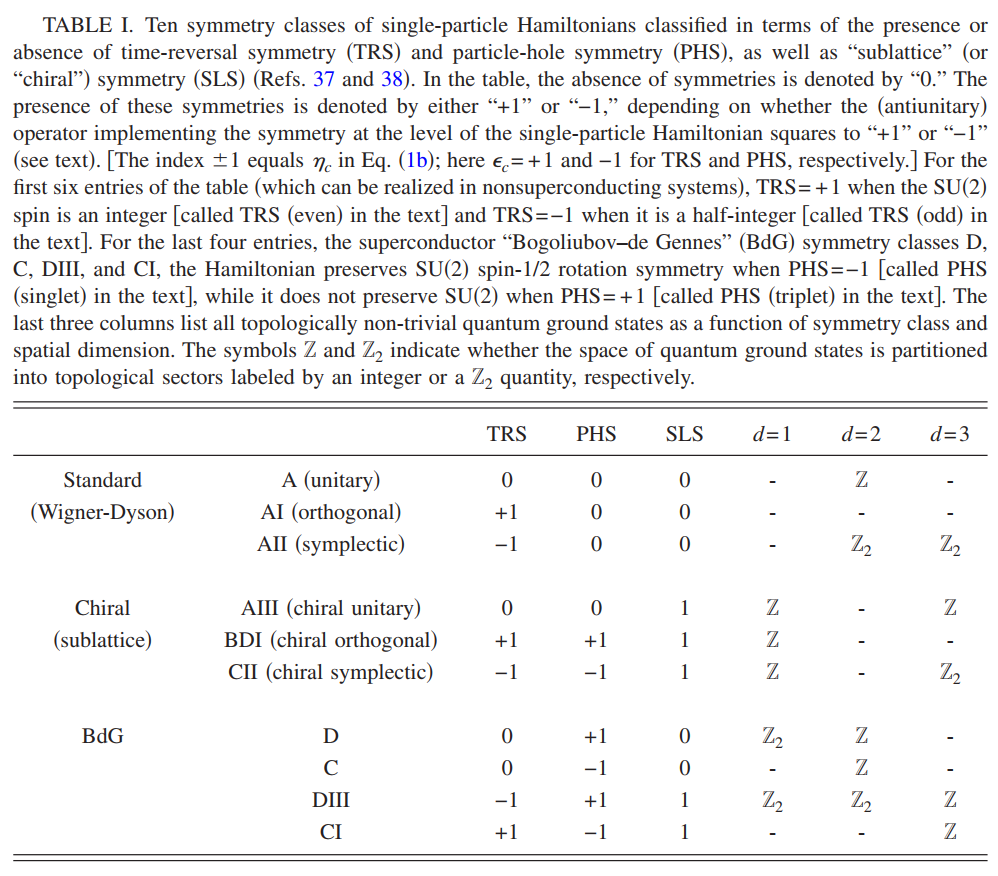
这是根据手性对称(sublattice symmetry or chiral symmetry),时间反演对称(Time reversal symmetry),粒子空穴对称(Particle hole symmetry)对哈密顿量进行分类,首先来理解一下为什么会有10个分类.
首先TRS与PHS都是反幺正操作算符,对应的矩阵就是一个反幺正矩阵,可以写作$\hat{U}\hat{\mathcal{K}}$,其中$\hat{U}$是个幺正操作矩阵,$\hat{\mathcal{K}}$是复数共轭操作.TRS与PHS的”本征值”都可以是$-1,+1,0$这三种选择,$0$则代表没有这种对称性,$\pm 1$则代表将这个算符对单粒子算符作用两次之后是$+1$还是$-1$,所以它们两个的组合共有$9$种不同的结果.手性对称(SLS)可以由这两种对称性组合出来,
\[SLS=TRS\times PHS\]所以由TRS与PHS确定的9个组合种,其中的8个可以通过SLS的有无来确定,而唯一无法确定的就是第9个$(TRS,PHS)=(0,0)$这种情况,此时两种对称性都不存在,但是却可以存在SLS或者不存在SLS,这又会有两种情况,所以加上前面的8种情况,就一共有10种分类.
上面表种后面三列代表着10重分类下,不同空间维度标志其拓扑性质不变量的形式.$Z$表示整数,$Z_2$则表示${-1,+1}$
对称操作算符
这里存在两种类型的对称操作算符
\[\begin{equation} \begin{aligned} &P:\mathcal{H}=-P\mathcal{H}P^{-1},\quad PP^\dagger=1,\quad P^2=+1\\ &C:\mathcal{H}=\epsilon_cC\mathcal{H}^{T}C^{-1},\quad CC^\dagger=1,\quad C^T=\eta_c C \end{aligned} \end{equation}\]对于$C$类型的算符$\epsilon_c=1$代表TRS算符,$\epsilon_c=-1$代表PHS算符.
$\eta_c=\pm 1$:$(\epsilon_c,\eta_c)=(1,1)$则代表spinless(整数自旋)的TRS算符,$(\epsilon_c,\eta_c)=(1,-1)$代表spinfull(自旋$\frac{1}{2}$)的TRS算符.同样的$(\epsilon_c,\eta_c)=(-1,1)$表示PHS自旋三重态的BdG哈密顿量,$(\epsilon_c,\eta_c)=(-1,-1)$表示PHS自旋单重态BdG哈密顿量.
如果存在PHS,则系统的能量一定是关于零对称分布的, 如果存在TRS那么一定会有Kramers简并存在.即使对这些对称算符进行幺正变换,但是其对应的$\epsilon_c,\eta_c$是不会改变的.
这里$P$型对称也会使得哈密顿量的能谱是对称的(手性对称),当这种对称性存在的时候,可以将哈密顿量变成off-diagonal的形式,可以通过对单个分块矩阵的winding number研究来区分哈密顿量的拓扑分类.
当哈密顿量同时具有$P,C$型的对称性之后, 将会自动存在一个不同于$C$的对称操作$C^{‘}$
\[\mathcal{H}=\epsilon^{}_cC^{'}\mathcal{H}^TC^{'-1},\quad C^{'}=PC,\quad \epsilon^{'}_c=-\epsilon_c\]在动量空间中,哈密顿量$H(\mathbf{k})$在这些算符的操作下变换为
\[\begin{equation}\begin{aligned} &\mathcal{T}H(\mathbf{k})\mathcal{T}=H(-\mathbf{k})\qquad TRS\\ &\mathcal{C}H(\mathbf{k})\mathcal{C}=-H(-\mathbf{k})\qquad PHS\\ &\mathcal{S}H(\mathbf{k})\mathcal{S}=-H(\mathbf{k})\qquad \textrm{Chiral Symmetry}\\ \end{aligned}\end{equation}\]可以将10中不同的分类划分为3大类
- standard classes:{A,AI,AII}
- chiral class:{AIII,BDI,CII}
- BdG class:{D,C,DIII,CI}
半整数自旋存在TRS(AII)
\[is_y\mathcal{H}^T(-is_y)=\mathcal{H}\qquad\text{TRS odd}\]SU(2)自旋旋转对称,spinless TRS对称操作(AI)
\[\mathcal{H}^T=\mathcal{H}\qquad\text{TRS even}\]手性对称(AIII)
\[c_z\mathcal{H}c_z=-\mathcal{H}\]这个对称性的存在会使得能量本征值总是成对出现(正负成对), 一个本征能量为$E$的$\psi$, 一定存在能量为$-E$的$c_z\psi$.
当再存在TRS之后,哈密顿量属于CII类.如果同时具有SU(2),TRS,Chiral symmetry则属于BDI类(此时是spinless粒子).
AIII类的哈密顿量可以被解释为类似BdG哈密顿量,具有TRS并且在SU(2)的子群U(1)操作下是不变的.
体边对应关系(holographically):物理系统的边界态准确的反映体态的量子拓扑物态.
BdG Class
一般超导BdG哈密顿量可以表示为
\[H=\frac{1}{2}({\bf c^\dagger,c})\mathcal{H}_4\left(\begin{array}{c} {\bf c}\\{\bf c^\dagger}\end{array}\right),\quad \mathcal{H}_4=\left(\begin{array}{cc}\Theta &\Delta\\-\Delta^{*} &-\Theta^T\end{array}\right)\label{bdg}\]这里$\mathcal{H}4$是$4N\times 4N$的矩阵, 表示系统中共有$N$个轨道(格点位置), ${\bf c}=({\bf c\downarrow,c_\uparrow})$, 矩阵的元素满足$\Theta=\Theta^\dagger$(Hermiticity)和$\Delta=-\Delta^T$(Fermi statistic). BdG哈密顿量(\ref{bdg})满足
\[(a):\quad\mathcal{H}_4=-t_x\mathcal{H}_4^Tt_x\]这是一个C类型的对称性$(\epsilon_c,\eta_c)=(-1,+1)$, 被称为粒子空穴对称(PHS)(三重态).
根据是否存在时间反演对称(TRS)表示为
\[(b):\quad is_y\mathcal{H}_4^T(-is_y)\qquad [\text{TRS(odd)}]\]是否存在SU(2)的自旋转动对称表示为
\[(c):\quad [\mathcal{H}_4,J_a]=0,\quad J_a:=\left(\begin{array}{c}s_a&0\\ 0&-s_a^T\end{array}\right),\quad a=x,y,z\quad[\text{SU(2) symmetry}]\]Class $C$和$CI$与singlet 超导体相对应, $D$和$DIII$则与triplet超导体相对应, 一个体系中也可以同时存在单重态和三重态的序参量.
Class D
此时哈密顿量只有PHS,并不存在TRS和SU(2)不变性.此时的BdG哈密顿量满足李代数SO(4m), 任何一个元素$\mathcal{H}_4\in SO(4m)$可以被一个SO(4m)的矩阵$g$对角化,$g\mathcal{H}_4g^{-1}=\text{diag}(\epsilon,-\epsilon)$,这里$\epsilon=\text{diag}(\epsilon_1,\epsilon_2,\cdots)$, 能谱是满足粒子空穴对称的.
一个 class D 的BdG 2维的spinless手性p波超导体为
\[H=\frac{1}{2}\sum_k(c^\dagger_kc_{-k})h(k)\left(\begin{array}{c}c_k\\c^\dagger_{-k}\end{array}\right),\\ h(k)=\bar{\Delta}(k_xt_x+k_yt_y)+\epsilon_kt_z\label{h1}\]这里$\bar{\Delta}\in\mathbb{R}$是超导序参量的幅值,$\epsilon_k$代表单粒子能量色散, 哈密顿量具有粒子空穴对称$h(k)=-t_xh^T(-k)t_x$.
Class DIII
class DIII 同时满足条件(a)和(b), A set of matrices which simultaneously satisfy (a) and (b) does not form a subalgebra of so(4m) but consists of all those elements of the Lie algebra so(4m) which are not elements of the sub-Lie algebra u(2m)
将(a)和(b)结合起来, 可以发现class DIII中的成员与幺正矩阵$t_x\otimes s_y$满足反对易关系
\[\mathcal{H}_4=-t_x\otimes s_y\mathcal{H}_4(t_x\otimes s_y)\]在这个情况下class DIII哈密顿量由手性结构, 可以对基矢进行一个手性变换, 此时哈密顿量形式为
\[\mathcal{H}_4=\left(\begin{array}0&D\\ D^\dagger&0\end{array}\right),\quad D=-D^T\]一个class DIII的实例为$p_x(or p_x)$波超导体, d矢量并不指向$z$方向, 两个手性相反的$p$波超导体的叠加$(p_x+ip_y and p_x-ip_y)$同样落在这个分类中, 这种情况下哈密顿量可以被表示为
\[H=\frac{1}{2}\sum_k({\bf c^\dagger_k,c_{-k}})\left(\begin{array}{cc}\Theta_k&\Delta_k\\\Delta^\dagger_k&-\Theta^T_{-k}\end{array}\right)\left(\begin{array}{c}{\bf c_k}\\{\bf c^\dagger_{-k}}\end{array}\right)\label{h2}\]行矢量$({\bf c^\dagger_k,c_{-k}})=(c^\dagger_{k\uparrow},c^\dagger_{k\downarrow},c_{-k\uparrow},c_{-k\downarrow})$, 矩阵元素分别为
\[\Theta_k=\epsilon_ks_0\quad \Delta_k=\bar{\Delta}\left(\begin{array}{cc}k_x+ik_y&0\\0&-k_x+ik_y \end{array}\right)\]可以写成矢量${\bf d}_k=\bar{\Delta}(-k_x,k_y,0)$, 超导序参量形式为
\[\Delta_k=({\bf d_k\cdot s})(is_y)\]这里可以发现哈密顿量(\ref{h2})其实是哈密顿量(\ref{h1})的$h(k_x,k_y),h(-k_x,-k_y)$的直积形式,其实也就是把本来spinless的基矢变成spinfull$({\bf c_k^\dagger,c_k})\rightarrow({\bf c_{k\uparrow}^\dagger,c_{k\downarrow}^\dagger,c_{-k\uparrow}^\dagger,c_{-k\downarrow}^\dagger})$.
BdG class with $S_z$ conservation
如果BdG哈密顿量具有在自旋空间沿z方向的旋转不变性,则满足条件为$[\mathcal{H}_4,J_a]=0$,哈密顿量可以表示为
\[\mathcal{H}_4=\left(\begin{array}{cccc}a&0&0&b\\ 0&a^{'}&-b^T&0\\ 0&-b^*&-a^T&0\\ b^\dagger&0&0&-a^{'T}\end{array}\right)\qquad a^\dagger=a,\quad a^{'\dagger}=a^{'}\]由于$\mathcal{H}_4$的这种稀疏结构,可以把$4N\times 4N$的矩阵重排为$2N\times 2N$.
\[H=({\bf c^\dagger_\uparrow,c_\downarrow})\left(\begin{array}{cc}a&b\\b^\dagger&-a^{'T}\end{array}\right)\left(\begin{array}{c}{\bf c_\uparrow}\\{\bf c^\dagger_\downarrow}\end{array}\right)+\frac{1}{2}\text{Tr}[a^{'}-a]\]这个哈密顿量是traceless的.当一个哈密顿量在自旋空间中关于z方向是旋转不变的时候,可以有下面的形式
\[H=({\bf c^\dagger_\uparrow,c_\downarrow})\mathcal{H}_2\left(\begin{array}{c}c_\uparrow\\c^\dagger_\downarrow\end{array}\right),\quad \mathcal{H}_2=\left(\begin{array}{c}\xi_\uparrow&\delta\\\delta^\dagger&-\xi_\downarrow^T\end{array}\right)\]这里的$\xi_\sigma=\xi_\sigma^\dagger$,当没有额外的对称性限制时,这个哈密顿量属于calss A.实现这个类的物理系统可以是一个2D的spinfull的手性$p$波超导体$(p\pm ip)$,此时的矢量${\bf d}$是平行于$z$方向的
\[{\bf d}_k=\hat{z}\bar{\Delta}(k_x+ik_y)=\bar{\Delta}(0,0,k_x+ik_y)\]一个spinfull的手性$(p\pm ip)$波超导体可以表示为
\[H=\sum_k(c^\dagger_{k\uparrow},c_{-k\downarrow})\left(\begin{array}{cc}\xi_{\uparrow k}&\delta_k\\\delta_k^\dagger&-\xi_{\downarrow -k}\end{array}\right)\left(\begin{array}{c}c_{k\uparrow}\\c_{-k\downarrow}\end{array}\right)\label{h3}\]这里$\delta_k=\bar{\Delta}(k_x+ik_y),\xi^T_{\uparrow/\downarrow,k}=\xi_{\uparrow/\downarrow,-k},\delta_k^T=\delta_{-k}$.
calss C [full SU(2) symmetry]
前面已经讨论了在存在$z$方向自旋转动不变时哈密顿量满足的一些条件,这里进一步考虑体系具有全部的SU(2)旋转对称,此时$\xi_\sigma,\delta$会有限制
\[\xi_\downarrow=\xi_\uparrow=:\xi,\quad\delta=\delta^T\]这两个条件可以总结为
\[r_y\mathcal{H}_2^Tr_y=-\mathcal{H}_2\quad [\text{PHS(singlet)}]\]$r_\mu$被用来表示在超导中$S_z$分量$z$是守恒的,这是一个C类型的对称性满足$(\epsilon_c,\eta_c)=(-1,-1)$,被称为PHS(signlet).
class C的BdG实例是2D的$(d+id)$波超导体,哈密顿量表示为(\ref{h3})的形式,矩阵元素满足$\xi_{\uparrow k}=\xi_{\downarrow k}=\epsilon_k$
\[\delta_k=\Delta_{x^2-y^2}(k_x^2-k_y^2)+i\Delta_{xy}k_xk_y\label{h4}\]这里$\Delta_{x^2-y^2}$和$\Delta_{xy}$分别是$d_{x^2-y^2}$和$id_{xy}$超导体的序参量.
class CI [full SU(2) symmetry + TRS]
当同时存在时间反演对称和全部的SU(2)对称后, 限制条件变为
\[\xi^*=\xi,\quad\delta^*=\delta\]哈密顿量满足
\[r_y\mathcal{H}_2^Tr_y=-\mathcal{H}_2,\quad \mathcal{H}_2^*=\mathcal{H}_2\]当把这两个条件结合起来之后, 可以得到一个P类型的对称性, $r_y\mathcal{H}2r_y=-\mathcal{H}_2$, 当对$r\mu$做一个轮换操作之后$(r_x,r_y,r_z)\rightarrow (r_x,-r_z,r_y)$,在这个基矢下, 可以把class CI的哈密顿量表示为off-diagonal形式
\[\mathcal{H}_2=\left(\begin{array}{cc}0&D\\ D^\dagger&0\end{array}\right),\quad D=\delta-i\xi=D^T\]class CI的一个BdG哈密顿量的实例是2D的$d$-波超导体,此时序参量也可以被(\ref{h4})描述,此时$\Delta_{xy}=0,\Delta_{x^2-y^2}\neq 0$.
class AIII($S_z$ conservation + TRS)
如果同时存在自旋$z$分量守恒, 且满足TRS, 可以得到
\[\xi^T_\uparrow,\quad\delta=\delta^\dagger\]可以将哈密顿量表示为
\[r_y\mathcal{H}_2r_y=-\mathcal{H}_2\]此时如果把$r_\mu$视为$c_\mu$,那么这就是子晶格对称性(手性对称),因此当一个BdG哈密顿量同时满足TRS和SU(2)自旋某一个分量守恒时,可以认为是没有TRS的calss AIII中的一员.
满足这个分类的BdG哈密顿量是2D的$p$波超导体($p_x\quad\text{or}\quad p_y$),此时矢量${\bf d}$是平行于$z$方向的
\[{\bf d}_k=\bar{\Delta}\hat{z}k_{x,y}\]Dirac 理论
拓扑等价/不等价
一个满足对称性的最小哈密顿量
\[H({\bf k})=m\gamma_0+\sum_{i=1}^Nk_i\gamma_i\label{eq1}\]这里的$N$表示空间维度,$\gamma_i$是满足反对易关系的厄米矩阵,${\gamma_i,\gamma_j}=2\delta_{ij}$,而满足对称性即意味着,在一个g对称操作下
\[gH({\bf k})g^{-1}=H(g{\bf k})\]最小哈密顿量的意思是取能够同时满足对称性和反对易关系的最小维度的矩阵.
哈密顿量(\ref{eq1})的能谱为
\[\pm\sqrt{m^2+{\bf k}^2}\]显然$m>0$的所有态都是拓扑等价的,$m<0$的态也都是拓扑等价的,如何判断$m>0$与$m<0$是否为拓扑等价?
方法:在不扩大维度的情况下,来寻找一个额外的质量项,如果存在一个同纬度的矩阵$\tilde{\gamma}_0$,它与所有的$\gamma_i$都反对易,而且满足所有的对称性,那么就可以在原来的哈密顿量中增加一项$\tilde{m}_0\tilde{\gamma}_0$,从而能谱变为$\pm\sqrt{m^2+\tilde{m}_0^2+{\bf k}^2}$,此时当$m\rightarrow -m$进行演化的时候,只要保证$\tilde{m}_0\neq 0$,这个演化不会有能隙关闭的过程,是个绝热演化.相反的,如果不存在这样的质量项,当进行同样的演化过程的时候,由$m>0$到$m<0$必然会经历一次能隙的闭合,此时$m>0$与$m<0$是拓扑不等价的两个相.
$\mathcal{Z}\quad\text{or}\quad \mathcal{Z}_2$
要判断拓扑相的拓扑分类是$\mathcal{Z}$还是$\mathcal{Z}_2$,需要考察当把几个最小哈密顿量直和起来就可以加入额外的质量项.比如,当把两个最小哈密顿量直和起来,就可以加入额外的质量项,则说明两个拓扑态的直和是个平庸态,那么它对应的拓扑分类就是$\mathcal{Z}_2$.
Chern 绝缘体
以二维系统为例演示狄拉克理论的用法,二维情况下最小的Dirac模型为
\[H({\bf })=m\sigma_z+k_x\sigma_x+k_y\sigma_y\label{eq2}\]三个Pauli矩阵外加一个单位矩阵,可以构成二维矩阵的完备基矢,所以此时无法找到另外的$2\times 2$的厄米矩阵同时与三个Pauli矩阵都反对易.当把两个(\ref{eq2})直和起来之后,$\tau_0\otimes H({\bf k})$,此时仍然无法加入满足要求的质量项.如果把质量符号相反的最小模型直和起来,$\tau_z\otimes H({\bf k})$,此时就可以加入形如$\tau_x\sigma_0$的额外质量项.实际上,我们将任意多个质量同号的Chern剧院提直和起来,都不能加入额外的质量项;而每一对质量相反的Chern绝缘体之间总是可以加入额外的质量项,这索命无对称性的二维系统具有$\mathcal{Z}$的拓扑分量,其中拓扑不平庸的态统称为Chern绝缘体.
时间反演不变系统
这里分析时间反演不变的二维系统,$\mathcal{T}^2=-1$,假设时间反演操作为$\mathcal{T}=-i\sigma_y\mathcal{K}$,那么一个满足对称性的最小哈密顿量为
\[H({\bf k})=m\tau_y\sigma_z+k_x\tau_0\sigma_x+k_y\tau_0\sigma_y\label{eq3}\]此时可以加入的反对易质量项为$\tau_x\sigma_z,\tau_z\sigma_z$,但是这两项都破坏了时间反演对称,所以此时并不存在额外的质量项,可以在满足对称性的条件下仍然和(\ref{eq3})中的每一项都反对易.接下来考虑两个最小模型的直和形式,$\mu_0\otimes H({\bf k })$,可以发现此时可以加入形如$\mu_y\otimes\tau_x\sigma_z$的项,既满足对称性要求同时和所有的$\gamma$矩阵满足反对易关系.而对于质量相反的直和形式$\mu_z\otimes H({\bf k})$可以加入$\mu_x\tau_0\sigma_0$这样的额外质量项.由此可以得到时间反演不变的二维系统的拓扑分类是$\mathcal{Z}_2$.虽然此时无法加入满足时间反演不变的质量项,但是却可以加入破坏时间反演的质量项,这说明$\mathcal{Z}_2$分类中不平庸的态在破缺时间反演之后会变成平庸态,因此这个态被称为时间反演保护的拓扑绝缘体.
体态拓扑性质表征
当讨论体态性质的时候最常用到的就是谱投影子.当哈密顿量具有$P$型对称性的时候,投影子总可以变换成off-diagonal分块形式,此时可以对分块定义一个winding number来表征不同的拓扑相.当系统存在平移不变性时,总可以将基态看成是一个在BZ中满填充的$d$维费米球.能带结构则可以看成是BZ空间到Bloch哈密顿量的一个映射,对于谱投影算子,可以看做是倒空间元胞到确定的李群或者陪集流形的映射,这个通常被称为是算子空间或者目标空间.
对于一个本征方程
\[\mathcal{H}\rvert u_{\hat{a}}(k)\rangle=E_{\hat{a}}(k)\rvert u_{\hat{a}}(k)\rangle\]在确定$k$时满填充的Bloch态的投影子为
\[P(k)=\sum_{\hat{a}}^\text{filled}\rvert u_{\hat{a}}(k)\rangle\langle u_{\hat{a}}(k)\rvert\]这里定义一个$Q(k)$
\[Q(k)=2P(k)-1\]这个$Q$矩阵满足
\[Q^\dagger=Q,\quad Q^2=1,\quad\text{Tr}[Q]=m-n\]此时考虑的情况中又$m$个占据态,$n$个空态.当有不同的对称性存在时,会对Q有一些其他的对称限制.
先不考虑额外的对称性限制,此时投影子的取值是所谓的Grassmannian数$G_{m,m+n}(\mathbb{C})$:它是由一系列幺正矩阵的本征值组成,而且是$U(m+n)$中的一员.当考虑占据态的投影子时,将会有一个占据态的规范对称$U(m)$,同样的也会存在相似的空态规范对称$U(n)$.投影子可以被陪集$U(m+n)/U(m)\times U(n)\simeq G_{m,m+n}(\mathbb{C})\simeq G_{n,m+n}(\mathbb{C})$.对于陪集$G_{m,m+n}(\mathbb{C})$的元素可以表示为
\[Q=U\Lambda U^\dagger,\quad\Lambda=\text{diag}(\mathbb{I}_m,-\mathbb{I}_n),\quad U\in U(m+n)\]当存在TRS或者PHS时($C$型),它们是反幺正算符,会禁止耨写映射关系.而对于$P$型对称操作,投影子将会从$G_{n,m+n}(\mathbb{C})$变成$U(m)$
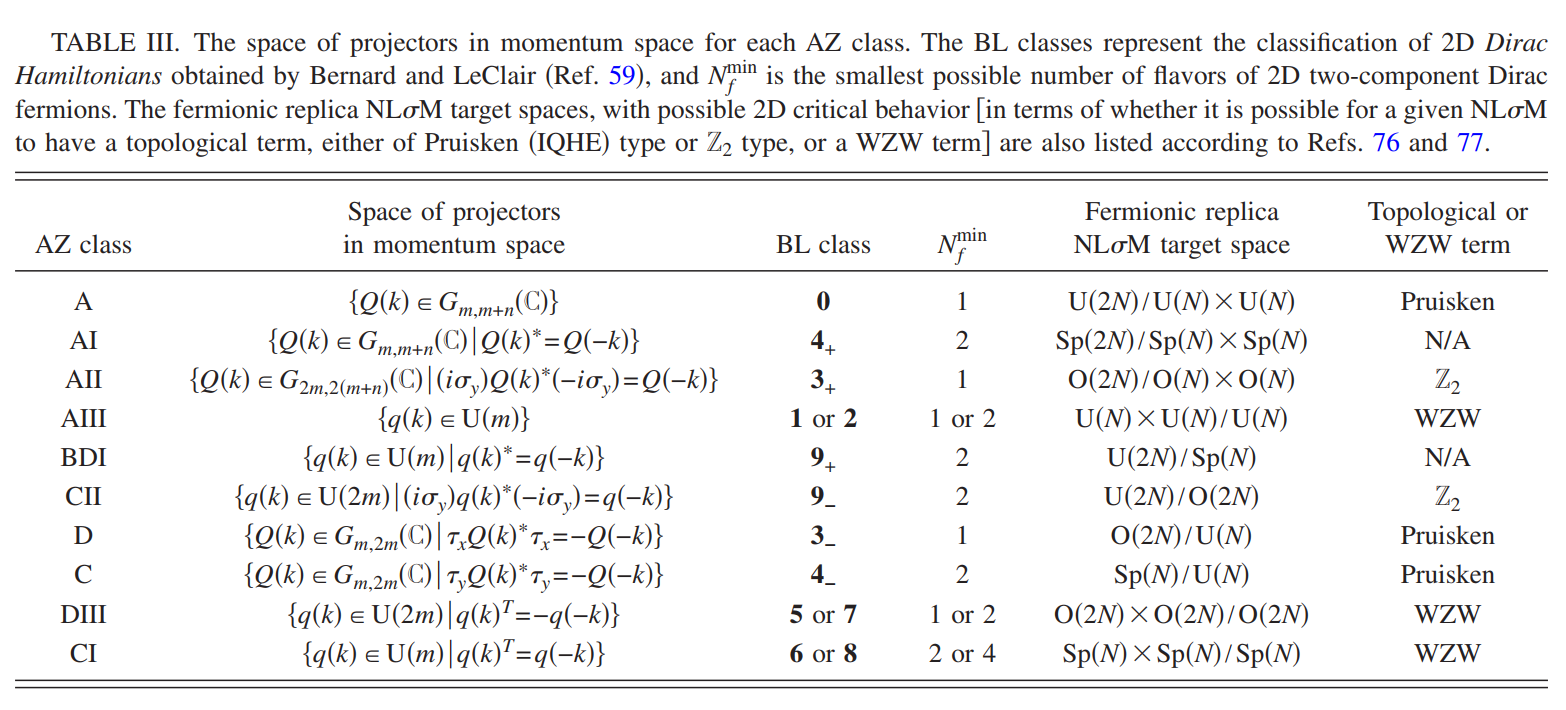
当考虑一些特定对称类下的投影子,是否可以通过连续变形相互转换的时候,这个连续变形过程中不会有能隙的关闭.在数学上这与投影子的拓扑空间的同伦群是相关联的.与两维空间项联系的同伦群$\pi_2[G_{m,m+n}(\mathbb{C})]=\mathbb{Z}$,表明此时投影子可以通过一些整数(Chern number)来区分,不同Chern number的投影子是不可以通过绝热演化相互转换的.
对于不存在任何离散对称性的情况(Class A),三维空间同伦群为
\[\pi_3[G_{m,m+n}(\mathbb{C})]\simeq{e}\]这里${e}$表示群只有一个单位元素,故此时再3D空间不存在winding的表示.(当$m=1$时存在一个偶然的winding,$\pi_3[G_{1,2}(\mathbb{C})]=\mathbb{Z}$,这是Hopf映射).虽然在Class A中三维时并不存在拓扑不同的相,但是当存在额外的离散对称性之后,是可以在3D存在不同的拓扑相的,因为这些离散的对称性会对$Q$有一定的限制,从而会影响群结构.
比如Class AII, 此时投影子满足$(i\sigma_y)Q^T(k)(-i\sigma_y)=Q(-k)$,是因为存在TRS的原因.当存在这个限制条件之后,两个不同的$Q$构型就有可能不会通过绝热演化相互变换,此时3D就有对应的拓扑分类.
分块 off-diagonal 投影子
当存在反幺正操作时(TRS or PHS),将会使得投影子在波矢$k$和$-k$处相互关联,因此TRS或者PHS会禁止动量空间中$Q$-field的某些构型,或者在BZ中将$k=-k$进行轨道折叠,从而改变拓扑结构.相反手型对称(SLS)是个幺正操作,会作用到Z中的每个波矢$k$上,因此这个对称性的作用就仅仅是改变投影子的目标流形.当存在手性对称的时候,可以把$Q$矩阵表示成off-diagonal的分块形式
\[Q=\left(\begin{array}{cc}0&q\\q^\dagger&0\end{array}\right)\]由于$Q^2=1$,则$q^\dagger q=qq^\dagger=1$,因此$q$肯定是$U(m)$中的一员.同样的,当存在其他对称性的时候,$q$也会受到一定的对称性限制.而且因为手性对称是$P$型的,所以此时投影子空间是$U(m)$,其对应的同伦群为
\[\pi_d[U(m)]\simeq\{\begin{array}{c}\{e\}\quad\text{for $d$ even}\\\mathbb{Z}\quad\text{for $d$ odd}\end{array}.\]当$m\geq(d+1)/2$,此时同伦群为
\[\pi_d[G_{m,m+n}(\mathbb{C})]\]当感兴趣的对称类允许不同拓扑构型的非平庸态出现,那么一个有用的工具就是利用量子化的拓扑不变量来区分这些不同的量子态.比如整数量子霍尔效应,其Hall电导$\sigma_{xy}$就是量子化的,它本质上是由$\pi_s[G_{m,m+n}(\mathbb{C})]=\mathbb{Z}$表征的winding number.在$\mathbb{Z}_2$拓扑绝缘体中,它就是$\mathbb{Z}_2$不变量,由于时间反演对称(TRS)的存在,可以通过$SU(2)$的Wilson loop的量子化值来表征.
Winding number in three diemsions
由于$\pi_3[U(m)]\simeq\mathbb{Z}$(for $m\geq 2$),在三维空间中,那些$Q$矩阵可以变换成off-diagonal形式的分类中,存在拓扑不等价的构型,它们之间不能通过绝热演化而相互转换.这些拓扑不等价的相可以通过winding number来biaozheng
\[\nu[q]=\int\frac{d^3k}{24\pi^2}\epsilon^{\mu\nu\rho}\text{Tr}[(q^{-1}\partial_\mu q)(q^{-1}\partial_\nu q)(q^{-1}\partial_\rho q)]\label{v}\]这里$q(k)\in U(m),\mu,\nu,\rho=x,y,z$,积分是对整个格点系统的布里渊区进行,它是一个三维的环($T^3$),对于一个连续模型,(\ref{v})的积分区域拓扑等价于一个三维的球($S^3$).其实winding表示的就是由$T^3$到$S^3$进行映射的时候, 这个映射可以将$S^3$覆盖的次数. 即使有些对称类$(DIII,CI,BDI,CII)$$的投影子同样可以表示为off-diagonal的形式,但是因为由额外对称性的限制,所以并不代表着它们的拓扑不等价类是可以取任何整数的.它们相对应的整数取值需要根据其表面上对称性允许的massless的Dirac费米子的数目来确定.
3D Dirac Hamintonian
通过对3D哈密顿量的研究,计算(\ref{v})中所表示的winding number来确定系统的拓扑性质,并且可以通过哈密顿量计算其对应的边界态.
3D four-component Dirac hamiltonian
一个(3+1)D的有质量Dirac哈密顿量表示为
\[\mathcal{H}=-\partial_\mu\alpha_\mu+m\beta,\quad\mu=x,y,z\label{dirac}\]这里$m\in\mathbb{R}$,标准的$\Gamma$矩阵为
\[\alpha_\mu=\tau_x\sigma_\mu=\left(\begin{array}{cc}0&\sigma_\mu\\\sigma_\mu&0\end{array}\right),\quad\beta=\tau_z=\left(\begin{array}{cc}1&0\\0&-1\end{array}\right),\quad\gamma^5=\tau_x=\left(\begin{array}{cc}0&1\\1&0\end{array}\right),\quad\mu=x,y,z\]在动量空间中哈密顿量表示为
\[\mathcal{H}=\alpha_\mu k_\mu+m\beta=\left(\begin{array}{cc}m&k\cdot\sigma\\ k\cdot\sigma&-m\end{array}\right)\label{dirac2}\]其能谱为$E(k)=\pm\sqrt{k^2+m^2}:=\pm\lambda(k)$
此时并没有明确哈密顿量的对称性,(\ref{dirac})可以实现class AII, AIII,DIII拓扑绝缘体.
Class AII
class AII中的3D Dirac哈密顿量(\ref{dirac2})满足$i\sigma_y\mathcal{H}^*(k)(-i\sigma_y)=\mathcal{H}(-k)$,是满足TRS的半整数自旋的拓扑绝缘体.
Class DIII
除了TRS, 当哈密顿量同样满足PHS$\tau_y\otimes\sigma_y\mathcal{H}^*\tau_y\otimes\sigma_y=-\mathcal{H}(-k)$,则3D Dirac哈密顿量(\ref{dirac})是class DIII中的一员,将(\ref{dirac2})进行幺正变换$\mathcal{H}\rightarrow\text{diag}(\sigma_0,-i\sigma_y)H\text{diag}(\sigma_0,+i\sigma_y)$变为
\[\mathcal{H}(k)=\left(\begin{array}{cc}m&k\cdot\sigma(i\sigma_y)\\(-i\sigma_y)k\cdot\sigma&-m\end{array}\right)\label{d3}\]可以发现哈密顿量满足
\[i\sigma_y\mathcal{H}^*(-i\sigma_y)=\mathcal{H}(-k),\qquad\tau_x\mathcal{H}\tau_x=-\mathcal{H}^*(-k)\]这个拓扑绝缘体哈密顿量(\ref{d3})描述超流$^3He $ B相的BW态BdG的费米子准粒子, 此时矢量${\bf d}$平行于动量${\bf d}_k\sim k$.
Class AIII
3D Dirac 哈密顿量由于存在手性对称$\tau_y\mathcal{H}\tau_y=-\mathcal{H}$可以视为class AIII中的拓扑绝缘体,通过基矢旋转$\tau_y\rightarrow\tau_z$将(\ref{dirac})变为off-diagonal分块对角形式
\[\mathcal{H}=-i\alpha_\mu\partial_\mu-i\beta\gamma^5m,\quad \mu=x,y,z\]在动量空间中
\[\mathcal{H}(k)=\left(\begin{array}{cc}0&k\cdot\sigma-im\\k\cdot\sigma+im&0\end{array}\right)\label{d5}\]手性对称会存在$\beta\mathcal{H}(k)\beta=-\mathcal{H}(k)$
投影子与winding number
2D两分量的有质量Dirac哈密顿量为$\mathcal{H}^\text{2D}\text{Dirac}(k_x,k_y)=k_x\sigma_x+k_y\sigma_y+m\sigma_z$是最简单的一个二维拓扑绝缘体的例子,其对应的Hall电导$\sigma{xy}=\text{sgn}(m)/2(e^2/h)$,如果将$(k_x,k_y,m)$看做是一系列可以绝热变化的参数之后,2D Dirac对应的$2\times 2$的哈密顿量正可以描述Abelian几何位相.$4\times 4$的Dirac哈密顿量(\ref{dirac2})可以看做是$2\times 2$实例$\mathcal{H}^\text{2D}_\text{Dirac}(k_x,k_y)$的一个一般推广,这个体系会存在非平庸的Non-Abelia贝利位相.这里来考虑哈密顿量
\[\mathcal{H}=\alpha_\mu k_\mu+m\beta=\left(\begin{array}{cc}m&k\cdot\sigma\\ k\cdot\sigma&-m\end{array}\right)\]的本征态,当$E(k)=-\lambda(k)$时
\[\rvert u_1(k)\rangle=\frac{1}{\sqrt{2\lambda(\lambda+m)}}\left(\begin{array}{c}-k_{-}\\ k_z\\ 0\\\lambda+m\end{array}\right)\] \[\rvert u_2(k)\rangle=\frac{1}{\sqrt{2\lambda(\lambda+m)}}\left(\begin{array}{c}-k_{z}\\ -k_{+}\\ \lambda+m\\0\end{array}\right)\]当$E(k)=+\lambda(k)$时
\[\rvert u_3(k)\rangle=\frac{1}{\sqrt{2\lambda(\lambda-m)}}\left(\begin{array}{c}k_{-}\\ -k_z\\ 0\\\lambda-m\end{array}\right)\] \[\rvert u_4(k)\rangle=\frac{1}{\sqrt{2\lambda(\lambda-m)}}\left(\begin{array}{c}k_z\\ k_+\\ \lambda-m\\0\end{array}\right)\]这里$k_\pm=k_x\pm ik_y$.如果$m>0$此时$\rvert u_{3,4}(k)\rangle$在$\lambda=m$时不是一个较好的定义.
接下来对占据态求解$Q$矩阵(也就是投影子)
$Q(k)=2P(k)-1=-\frac{1}{\lambda}(k_\mu\alpha_\mu+m\beta)$
通过对手性操作进行轮换$\tau_y\rightarrow\tau_z$,可以求解class AIII(\ref{d5})哈密顿量对应的$q$矩阵
\[q(k)=-\frac{1}{\lambda}(k_\mu\sigma_\mu-im)\label{q1}\]同样的,对于哈密顿量(\ref{d3}),其对应的投影子为
\[q(k)=i\sigma_y(k_\mu\sigma_mu-im)/\lambda,\qquad q^T(-k)=a(k)\]通过winding number的计算公式(\ref{v})表示$q(k)$从$S^3$到$U(2)$的一个映射,可以计算(\ref{q1})的winding为
\[\nu[q]=\frac{1}{2}\frac{m}{\rvert m\rvert}\]这里出现半整数$\frac{1}{2}$是利用连续模型描述时的普遍情况,因为用连续模型描述的时候,无穷远点是个奇点,此时的空间不是有界的,所以需要包括高能部分就会补充这种不足.
边界Dirac费米子
通常体态波函数的非平庸拓扑性质总是会存在无能隙的边界态,当$z$方向存在一个质量变化项
$m(z)\rightarrow\left{ \begin{array}{c}+m,\qquad z\rightarrow+\infty\ -m,\qquad z\rightarrow-\infty\end{array}\right.$
来研究局域在边界$z=0$上2D Dirac费米子解.对class AIII 的3D Dirac哈密顿量$\mathcal{H}=-i\alpha_\mu\partial_\mu-i\beta\gamma^5m(z)$
能量为$E(k_\perp)$的解为
$\Psi(z)=\left(\begin{array}{c}0\ a(k_\perp)\ b(k_\perp)\ 0\end{array}\right)\exp[-\int^zdz^{‘}m(z^{‘})]$
这里$k_\perp=(k_x,k_y),x_\perp=(x,y)$分别表示动量和位置坐标,系数$a(k_\perp),b(k_\perp)$满足方程
\[\left(\begin{array}{c}a(k_\perp)\\b(k_\perp)\end{array}\right)=\frac{e^{ik_\perp\cdot x_\perp}}{\sqrt{2}}\left(\begin{array}{c}e^{i\cdot\text{arg}(k_\perp)}\\\pm 1\end{array}\right)\]能量$E(k_\perp)=\pm\sqrt{k_x^2+k_y^2}$,下面再来讨论一下这些边界态对杂质的稳定性
- class AII and DIII
单个表面Dirac费米子的无能隙性质是受到TRS保护的,打开能隙将会违反Kramer定理,对于class AII只有空间均匀的微扰与TRS相兼容的是个常熟势$V$
\[\mathcal{H}=-i\partial_\mu\sigma_\mu+V,\quad\mu=x,y\]此时并不能打开能隙,而对于class DIII,基矢常熟势也将会被TRS所禁止.
- Class AIII
一个单个组分的2D Dirac费米子在class AIII中可以被静态均匀的矢量势微扰
\[\mathcal{H}=-i\partial_\mu\sigma_\mu+A_\mu\sigma_\mu,\quad\mu=x,y\]矢量势仅仅会改变node的位置,并不会打开能隙.
3D eight-component Dirac Hamiltonian
对于Class CI,CII 并不能由四分量的(3+1)D Dirac哈密顿量组成且存在无能隙的边界态,这里考虑八分量的(3+1)D Dirac哈密顿量.
Class CI
八分量3D Dirac 哈密顿量为
$\mathcal{H}=\left(\begin{array}{cc}0&D\ D^\dagger&0\end{array}\right),\quad D=i\sigma_y\beta(k_\mu\alpha_\mu-im\gamma^5)$
是Class CI的一员,因为满足$D^T(k)=D(-k)$,能谱为$E(k)=\pm\sqrt{k^2+m^2}=\pm\lambda$,每个本征值都是4重简并的.
off-diagonal形式对应的投影子为
\[Q(k)=2P(k)-1=-\frac{1}{\lambda}\mathcal{H}(k),\qquad q(k)=-\frac{1}{\lambda}i\sigma_y\beta(k_\mu\alpha_\mu-im\gamma^5)\]其对应的winding number可以被计算
\[\nu[q]=\frac{1}{2}\frac{m}{\rvert m\rvert}\times 2\]当把3D Dirac绝缘体在研$z$方向2D表面上截止是,可以得到两分量的表面Dirac费米子
\[\mathcal{H}=\left(\begin{array}{cc}0&d\\D^\dagger&0\end{array}\right),\qquad D=i\sigma_y(k_++A_x\sigma_x+A_y\sigma_y+A_z\sigma_z)\]这里已经包含了class CI允许的微扰$A_{x,y,z}\in\mathbb{C}$,可以检验$D^T(k)=D(-k)$.四分量无能隙Dirac 费米子可以面议任意三个复数值(六个实数)$A_{x,y,z}$.正如class AIII中的矢量势一样,$A_{x,y,z}$也仅仅是将Dirac节点的位置从(0,0)移动到$(k_x^0,k_y^0)$,这里的$(k_x^0,k_y^0)$满足方程
\[(k_x^0)^2-(k_y^0)^2-\text{Re}A^2+\text{Im}A^2=0\qquad k_x^0k_y^0+(\text{Re}A\cdot\text{Im}A)=0\]Class CII
八分量3D Dirac哈密顿量
\[\mathcal{H}=\left(\begin{array}{cc}0&D\\D^\dagger&0\end{array}\right),\quad D=k_\mu\alpha_\mu+m\beta=D^\dagger\]是class CII的一员,满足$i\sigma_y D^*(k)(-i\sigma_y)=D(-k)$,对应的能谱为$E(k)=\pm\sqrt{k^2+m^2}$,$Q,q$矩阵分别为
\[Q(k)=2P(k)-1=-\frac{1}{\lambda}\mathcal{H}(\lambda),\quad q(k)=-\frac{1}{\lambda}(k_\mu\alpha_\mu+m\beta)\]与classCI的3D Dirac绝缘体相比,在class CII 的Dirac质量项为$m\beta$而不是手性的$im\gamma^5$,由于这个不同,class CII对应的3D Dirac哈密顿量的winding number为
\[\nu[q]=0\]由于此时winding number等于0,沿$z$方向存在质量畴壁时,我们不能在class CII 的3D Dirac绝缘体中寻找到两组分的两维Dirac费米子.
考虑2D表面上最一般的一个Dirac哈密顿量的形式
\[\mathcal{H}=\left(\begin{array}{cc}0&D\\D^\dagger&0\end{array}\right),\quad D=\left(\begin{array}{cc}v_+&k_{-}+a\\k_+-\bar{a}&v^*_+\end{array}\right)=(k_x+ia)\sigma_x+(k_y+ia_y)\sigma_y+i\text{Im}v_+\sigma_z\]这里的微扰$a_{x,y}$和$v_+$是被class CII对称性允许的.这里可以发现这些表面Dirac费米子的无能隙性质在存在微扰时仍然是稳定的.考虑哈密顿量的行列式
\[\text{det}(DD^\dagger)=(\rvert v_+\rvert^2-\rvert k_+\rvert^2+\rvert a\rvert^2)^2-(\bar{a}k_{-}-ak_{+})^2\]当
\[\rvert k_+\rvert^2=\rvert v_+\rvert^2+\rvert a\rvert^2\qquad\text{and}\qquad(k_x,k_y)\perp(a_x,a_y)\]时行列式是消失的.这表明对于行列式总是可以找到一个波矢$(k_x,k_y)$其对应的能量本征值消失,从而不存在能隙.
参考
- 1.拓扑半金属的磁响应与拓扑绝缘体中的$d-2$为边界态(宋志达)
- 2.Classification of topological insulators and superconductors in three spatial dimensions
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |