这篇博客中,整理自己在学习拓扑绝缘体相关的拓扑场论过程中的一些概念整理和自己的笔记,主要是对文章进行翻译,过程中会加一点自己的笔记。

第一Chern数:对Berry 位相规范场的曲率在整个BZ中的积分。

在1D时,在绝热演化的泵浦循环周期中,电子极化或者净电荷泵浦数目正好对应于Berry位相在动量及参数混合空间中的积分,和Chern数也存在一定的关联(2D)。这个积分得到的整数正是量子化的拓扑数。

拓扑磁电效应(TME):外加一个电场,会在相同的方向上诱导出磁场,其比值是个普适的常数,一个奇数乘以乘以精细结构常数$\alpha=e^2/(\hbar c)$。

第一Chern数及(2+1)维拓扑响应函数

一个(2+1)维的紧束缚哈密顿量为

\[H=\sum_{m,n;\alpha,\beta}c^\dagger_{m\alpha}h^{\alpha\beta}_{mn}c_{n\beta}\]

在实空间中,矩阵的维度大小及对应着能带数目,$\alpha,\beta=1,2,\cdots,N$。当系统具有平移对称性的时候$h^{\alpha\beta}_{mn}=h^{\alpha\beta}(\vec{r}_m-\vec{r}_n)$哈密顿量可以在Bloch基矢下写成对角形式

\[H=\sum_{\bf k}c^\dagger_{\mathbf{k}\alpha}h^{\alpha\beta}({\bf k})c_{\mathbf{k}\beta}\]

当存在外部电磁场耦合时

\[h^{\alpha\beta}_{mn}\rightarrow h^{\alpha\beta}_{mn}e^{iA_{mn}}\]

这里$A_{mn}$是定义在离散格点上的规范势。在线性阶近似下,耦合电磁场的哈密顿量为

\[H\simeq\sum_{\bf k}c^\dagger_{\bf k}h({\bf k})c_{\bf k}+\sum_{\bf k,q}A^i(-{\bf q})c^\dagger_{\bf k+q/2}\frac{\partial h({\bf k})}{\partial k_i}c_{\bf k-q/2}\]

系统对外场$A^i({\bf q})$的直流响应可以通过标准的Kubo公式得到

\[\sigma_{ij}=\text{lim}_{\omega\rightarrow 0}\frac{i}{\omega}Q_{ij}(\omega+i\delta),\quad Q_{ij}(i\nu_m)=\frac{1}{\Omega\beta}\sum_{\mathbf{k},n}\text{Tr}\{J_i({\bf k})G[\mathbf{k},i(\omega_n+\nu_m)]\cdot J_j(\mathbf{k})G(\mathbf{k},i\omega_n)\}\label{h4}\]

对于直流电$J_i({\bf k})=\frac{\partial h({\bf k})}{\partial k_i},i,j=x,y$,格林函数$G(\mathbf{k},i\omega_n)=[i\omega_n-h({\bf k})]^{-1}$,$\Omega$表示系统的表面积。当系统是个绝缘体的时候,$M$个占据态,c此时系统的纵向电导为零$\sigma_{xx}=0$,而横向电导为

\[\sigma_{xy}=\frac{e^2}{h}\frac{1}{2\pi}\int dk_x\int dk_yf_{xy}({\bf k}),\quad f_{xy}({\bf k})=\frac{\partial a_y({\bf k})}{\partial k_x}-\frac{\partial a_x({\bf k})}{\partial k_y},\\ a_i({\bf k})=-i\sum_{\alpha\in\text{occ}}\langle\alpha\mathbf{k}\rvert\frac{\partial}{\partial k_i}\rvert\alpha\mathbf{k}\rangle,\quad i=x,y\]

物理上$a_i({\bf k})$是动量空间中Berry位相规范场的$U(1)$分量。量子化的第一Chern数为

\[C_1=\frac{1}{2\pi}\int k_x\int k_y f_{xy}({\bf k})\in Z\]

对于任意定义在BZ上的连续态$\rvert\alpha\mathbf{k}\rangle$都是满足的。由于电荷守恒,Hall效应响应为$j_i=\sigma_H\epsilon^{ij}E_j$同样会诱导出另外一个响应方程

\[j_i=\sigma_H\epsilon^{ij}E_j\rightarrow\frac{\partial\rho}{\partial t}=-\nabla\cdot{\bf j}=-\sigma_H\nabla\times \mathbf{E}=\sigma_H\frac{\partial B}{\partial t},\rightarrow\rho(B)-\rho_0=\sigma_HB\label{h1}\]

这里$\rho_0=\rho(B=0)$是基态的电荷密度。将(\ref{h1})结合磁轭城一个协变形式为

\[j^\mu=\frac{C_1}{2\pi}\epsilon^{\mu\nu\tau}\partial_\nu A_\tau\label{h2}\]

这里$\mu,\nu,\tau=0,1,2$分别是时间和空间索引。此时选择自然单位制$e=\hbar=1,e^2/h=1/2\pi$。

响应(\ref{h2})可以有外场$A_\mu$的Chern-Simons拓扑场论描述

\[S_\text{eff}=\frac{C_1}{4\pi}\int d^2x\int dt A_\mu\epsilon^{\mu\nu\tau}A_\tau\]

由$\delta S_\text{eff}/\delta A_\mu=j^\mu$既可以得到响应电流(\ref{h2})。这样的有效作用量是拓扑不变的,和第一Chern数的性质相同,所有量子霍尔态的拓扑响应都可以通过Chern-Simons理论来描述。

Example:Two band models

考虑一个实际的两带模型

\[h({\bf k})=\sum_{a=1}^3[d_a({\bf k})\sigma_a+\epsilon({\bf k})\mathbb{1}]\]

这里$\mathbb{1}$是$2\times 2$的单位矩阵,$\sigma_a$是Pauli矩阵,这里$\sigma_a$可以表示自旋或者轨道,如果是真自旋则$\sigma_a$在时间反演操作下是增加一个负号的,如果$d_a({\bf k})$是奇函数,那么哈密顿量是满足时间反演不变的。如果任何一个$d_a$包含常数项,那么这个模型是破坏时间反演的。如果$\sigma_a$表示赝自旋(轨道),此时$\mathcal{T}^2=1$,只有$\sigma_y$在时间反演操作下出现一个负号,$\sigma_x,\sigma_z$都是不变的。单位矩阵在时间反演操作下是不变的,所以$\epsilon({\bf k})$在时间反演操作下是偶函数。上面哈密顿量对应的能谱为$E({\bf k})=\epsilon({\bf k})\pm\sqrt{\sum_ad^2_a({\bf k})}$。

在单粒子哈密顿量$h({\bf k})$中,矢量${\bf d(k)}$就像是作用在两能级赝自旋$\sigma_i$上的Zeeman场,占据态能带满足$[{\bf d(k)\cdot\sigma}]\rvert -,\mathbf{k}\rangle=-\rvert{\bf d(k)}\rvert\rvert-,\mathbf{k}\rangle$,这表明spinor的自旋极化方向为${\bf -d(k)}$,因此在$\rvert-,\mathbf{k}\rangle$上沿着某个${\bf k}$空间的路径$C$进行绝热演化时获得的Berry位相等于自旋$1/2$的粒子在磁场中沿着$\mathbf{d}(C)$绝热旋转时获得的Berry位相,着正就是由路径$\mathbf{d}(C)$所张开的立体角的一半。因此第一Chern数$C_1$可以被${\bf d(k)}$围绕原点的winding来确定

\[C_1=\frac{1}{2\pi}\int dk_x\int dk_y\hat{\bf d}\cdot\frac{\partial\hat{\bf d}}{\partial k_x}\times\frac{\partial\hat{\bf d}}{\partial k_y}\label{c1}\]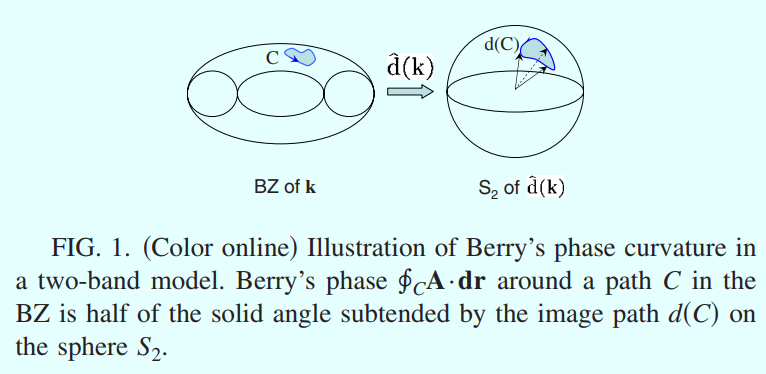

一个实际的物理模型为

$h({\bf k})=\sin k_x\sigma_x+\sin k_y\sigma_y+(m+\cos k_x+\cos k_y)\sigma_z$

这里$\epsilon({\bf k})=0,{\bf d(k)}=(\sin k_x,\sin k_y,m+\cos k_x+\cos k_y)$,体系的Chern数为

\[C_1=\left\{\begin{array}{c}1\qquad\text{for $0<m<2$}\\-1\qquad\text{for $-2<m<0$}\\0\qquad\text{otherwise}\end{array}\right.\]

在$m\rightarrow 2$的连续极限下,模型可以约化为(2+1)-D的有质量Dirac哈密顿量

\[{\bf h(k)}=k_x\sigma_x+k_y\sigma_y+(m+2)\sigma_z=\left(\begin{array}{cc}m+2&k_x-ik_y\\ k_x+ik_y&-m-2\end{array}\right)\]

在实空间中的紧束缚形式为

\[H=\sum_n[c^\dagger_n\frac{\sigma_z-i\sigma_x}{2}c_{n+\hat{x}}+c^\dagger_n\frac{\sigma_z-i\sigma_y}{2}c_{n+\hat{y}}+\text{H.c}]+m\sum_nc^\dagger_n\sigma_zc_n\label{h3}\]

这个模型可以描述量子反常霍尔效应,体系统是存在自旋轨道耦合($\sigma_x,\sigma_y$)以及铁磁极化$\sigma_z$。

维度约化

为了研究第一Chern数和拓扑响应之间的联系,可以通过维度约化来进行,首先在一个圆柱结构上研究量子霍尔态。一个非平庸的量子霍尔系统会存在手性边界态,对于最简单的Chern数$C_1=1$的情况,系统每个边界上都会存在一支手性费米子。可以将哈密顿量(\ref{h3})放在一个圆柱体结构上进行计算(一个方向是周期边界,另外一个方向是开边界)。此时周期边界方向的的$k$是一个好量子数,进行一个部分Fourier变换

$c_{k_ya}(x)=\frac{1}{\sqrt{L_y}}\sum_yc_\alpha(x,y)e^{ik_yy}$

这里的$(x,y)$表示正方点整上的坐标,最后可以将哈密顿量(\ref{h3})改写为

$H=\sum_{k_y,x}[c^\dagger_{k_y}(x)\frac{\sigma_z-i\sigma_x}{2}c_{k_y}(x+1)+\text{H.c}]+\sum_{k_y,x}c^\dagger_{k_y}(x)[\sin k_y\sigma_y+(m+\cos k_y)\sigma_z]c_{k_y}(x)\equiv\sum_{k_y}H_\text{1D}(k_y)$

在经过这个变换之后就可以将原本的2D系统看做是一个$L_y$依赖的1D紧束缚模型链,$L_y$表示在$y$方向上的周期晶格数目。而哈密顿量$H_\text{1D}$的本征值可以在每个$k_y$下通过数值方式求解,如下图所示

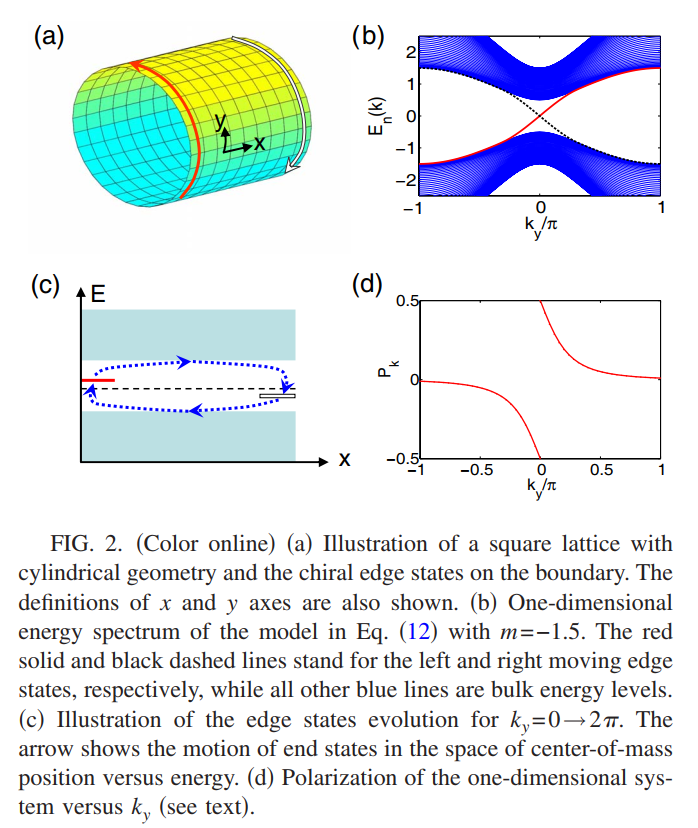
可以发现此时有个很明显的边界态会穿过体能隙,并且分别位于$x=0,L_x$这两个边界上。而且每条边界态的手性(费米速度)也是不同的,从图中也可以看出费米速度$v=\partial E/\partial k$对于左边界态总是正的,而对于右边界态总是负的,霍尔效应可以通过Laughlin的规范讨论来进行理解。考虑一个沿着$y$方向的电场$E_y$,可以表示为

$A_y=-E_yt,\quad A_x=0$

将哈密顿量改写为$H=\sum_kH_\text{1D}(k_y+A_y)$,沿着$x$方向的电流为

$J_x=\sum_{k_y}J_x(k_y)$

$J_x(k_y)$是一维系统的电流,此时2D系统的Hall响应可以通过参数化的1D系统$H_\text{1D}$决定,含时变化为$q(t)-k_y+A_y(t)$。规范势$A_y$对应着一个通量$\Phi=A_yL_y$穿过整个圆柱体结构,在一个周期变化中$0\leq t\leq2\pi/L_yE_y$通量从$0$变化到$2\pi$,而这个过程中流过系统的电荷为

$\Delta Q=\int_0^{\Delta t}dt\sum_{k_y}J_x(k_y)\equiv\sum_{k_y}\Delta P_x(k_y)\rvert_0^{\Delta t}$

一个周期中$\Delta t=2\pi/L_yE_y$,在第二个恒等式中利用了1D系统中电荷极化与电流的关系$T_x(k_y)=dP_x(k_y)/dt$,在热力学极限下系统总是处在$H_{1D}[q(t)]$的基态中,因此极化的改变$\Delta P_x(k_y)=P_x(k_y-2\pi/L_y)-P_x(k_y)$。当$L_y\rightarrow\infty$时,$\Delta Q$表示为

\[\Delta Q=-\int_0^{2\pi}dk_y\frac{\partial p_x(k_y)}{\partial k_y}\]

穿过圆柱体结构的通量变化导致的Hall效应所产生的的电荷流动等于在一维系统$H_{1D}(k_y)$当$k_y$从0变化到$2\pi$时的电荷流动。从Hall响应可以得到$\Delta Q=\sigma_H\Delta tE_yL_y=2\pi\sigma_H$是个量子化的整数,可以从1D的图像上进行理解。当$k_y$在0到$2\pi$进行变化的时候,边界态的能量和位置将会发生变化,如上图所示。由于在左(右)边界态的能量总是增加(减少)随着$k_y$的变化,在一个半填充的系统中电荷总会被泵浦到左边界,这将会使得$\Delta Q=-1$。这个量子化的值可以通过计算极化$P_x(k_y)$来得到,如上图(d)所示,当$P_x$在一边发生一个跃变的时候,就会有$\Delta Q=-1$。

上面维度约化的研究可以适用于任何一个2D的绝缘体系统,对于一般的2D系统可以定义其对应的1D系统为

\[H_{1D}(\theta)=\sum_{k_x}c^\dagger_{k_x,\theta}h(k_x,\theta)c_{k_x,\theta}\]

此时用$\theta$代替了有方向的动量$k_y$,并且替代了$q(t)$,当$\theta$是含时的,可以通过Kubo公式(\ref{h4})来计算电流响应,只不过此时对$(k_x,k_y)$的求和变成了只对$k_x$进行求和。线性响应可以定义为

\[J_x(\theta)=G(\theta)\frac{d\theta}{dt},\quad G(\theta)=\text{lim}_{\omega\rightarrow 0}\frac{i}{\omega}Q(\omega+i\delta;\theta)\\ Q(i\omega_n;\theta)=-\sum_{k_x,i\nu_m}\text{Tr}\{J_x(k_x;\theta)G_{1D}[k_x,i(\nu_m+\omega_n);\theta]\times\frac{\partial h(k_x;\theta)}{\partial \theta}G_{1D}(k_x,i\omega_n;\theta\}\frac{1}{L_x\beta}\label{h5}\]

响应系数根据Berry位相规范场表示为

\[G(\theta)=-\int\frac{dk_x}{2\pi}f_{x\theta}(k_x,\theta)=\int\frac{dk_x}{2\pi}(\frac{\partial a_x}{\partial \theta}-\frac{\partial a_\theta}{\partial k_x}),\quad \int G(\theta)d\theta=C_1\in Z\]

如果选择一个合适的规范,使得$a_\theta$总是单只的,则$G(\theta)$可以进一步简化

$G(\theta)=\frac{\partial}{\partial \theta}(\int\frac{dk_x}{2\pi}a_x(k_x,\theta))\equiv\frac{\partial P(\theta)}{\partial \theta},\quad P(\theta)=\int dk_xa_x/2\pi$

这正是1D系统对应的电荷极化,响应函数变为$J_x=\partial P/\partial t$。因为电子极化P的定义是电子的质心位置偏移格点的大小,所以它的定义只有mod 1才是well defined。因此一个周期演化的变化量$\Delta P=P(\theta=2\pi)-P(\theta=0)$是个整数,等于$-C_1$,也正好对应着整个系统的电荷泵浦数目。

和量子Hall情况相似,电流响应将会导致电荷密度的响应,着可以通过电荷守恒条件来确定,当参数$\theta$同时具有时间和空间变化时$\theta(x,t)$,响应方程(\ref{h5})仍然适用,从连续性方程可得到

\[\frac{\partial\rho}{\partial t}=-\frac{\partial J_x}{\partial x}=-\frac{\partial^2P(\theta)}{\partial x\partial t}\rightarrow\rho=-\frac{\partial P(\theta)}{\partial x}\label{ha8}\]

这里电荷密度$\rho$是基于背景电荷而言。此时密度与电流响应可以写为

\[j_\mu=-\epsilon_{\mu\nu}\frac{\partial[\theta(x,t)]}{\partial x_\nu},\quad\mu,\nu=0,1\text{分别是时间和空间}\]

一般情况下当哈密顿量随着时间和空间是平缓变时,单粒子哈密顿量$h(k)$变为$h(k,x,t)=h[k,\theta(x,t)]$,其对应的本征态为$\rvert\alpha;k,x,t\rangle$,这里的$\alpha$是能带索引。定义在相空间中的Berry位相规范场

\[\mathcal{A}_A=-i\sum_\alpha\langle\alpha;q_A\rvert\frac{\partial}{\partial q_A}\rvert\alpha;q_A\rangle,\quad\mathcal{F}_{AB}=\partial_A\mathcal{A}_B-\partial_B\mathcal{A}_A\]

相空间流为

\[j^p_A=-\frac{1}{4\pi}\epsilon_{ABC}\mathcal{F}_{BC}\]

实际的物理流可以通过对波矢流型进行积分得到

$j_\mu=\int dkj^P_\mu=-\int\frac{dk}{2\pi}\epsilon^{\mu2\nu}\mathcal{F}_{2\nu},\quad\mu,\nu=0,1$

对于一个SSH模型

\[h(k,\theta)=\sin k\sigma_x+(\cos k-1)\sigma_z+m(\sin\theta\sigma_y+\cos\theta\sigma_z),\quad m>0\]

在$m«1$的极限下,将哈密顿量展开成连续模型$h(k,\theta)\simeq k\sigma_x+m(\sin\theta\sigma_y+\cos\theta\sigma_z)$,着是一个连续的(1+1)D Dirac模型,有一个实质量$m\cos\theta$和一个虚质量$m\sin\theta$,根据前面的讨论,此时极化$\int dk_xa_x/2$可以由矢量$\mathbf{d}(k)=(\sin k,m\sin\theta,m\cos\theta+\cos k-1)$所张开的立体角来决定,如下图所示

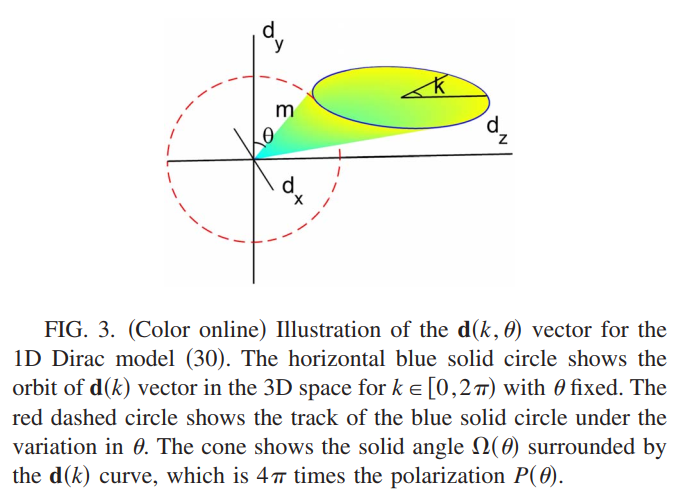
在$m«1$的即现在,可以发现张开的立体角$\Omega(\theta)=2\pi$,因此极化$P(\theta)\simeq\theta/2\pi$,响应电流为

\[j_\mu=-\epsilon_{\mu\nu}\partial_\nu\theta\]

在$\theta$场的畴壁上电荷积累为$Q=\int_{-\infty}^{+\infty}(d\theta/dx)(dx/2\pi)=-[\theta(+\infty)-\theta(-\infty)]/2\pi$。对于反位相的畴壁$\theta(+\infty)-\theta(-\infty)=\pi$,从而可以得到此时的存在分数电荷$q=\frac{1}{2}$。

(1+1)维$Z_2$分类粒子空穴对称绝缘体

对于一个一维的紧束缚哈密顿量

\[H=\sum_{mn}c^\dagger_{m\alpha}h^{\alpha\beta}_{mn}c_{n\beta}\]

粒子空穴变换定义为$c_{m\alpha}\rightarrow C^{\alpha\beta}c^\dagger_{m\beta}$,这里电荷共轭矩阵$C$满足$C^\dagger C=\mathbb{I},C^*C=\mathbb{I}$。在周期性边界条件下对称性要求

\[H=\sum_kc^\dagger_kh(k)c_k=\sum_kc_{-k}C^\dagger h(k)Cc^\dagger_{-k}\rightarrow C^\dagger h(-k)C=-h^T(k)\]

从上式可以知道,如果$E$是$h(0)$的本征值,那么$-E$也是,即哈密顿量的能谱是正负对称的。如果$h(k)$的维度是奇数,那么至少存在一个零能本征值$E=0$。此时因为$h$是traceless 的,因此化学势为零,这个系统不能被打开能隙,除非$h$的维度是偶数。

现在考虑两个满足粒子空穴对称的绝缘体哈密顿量$h_1(k),h_2(k)$。通常可以在两者之间插入一个连续的$h(k,\theta)$其定义为

\[h(k,0)=h_1(k),\quad h(k,\pi)=h_2(k)\]

而且总是可以找到一个合适的参数使得$\theta\in[0,\pi]$区间内$h(k,\theta)$总是有能隙的。总而言之,拓扑空间中所有1D拓扑绝缘体$h(k,\theta)$都是相互联系的,这也是Neumann–Wigner theorem保证的。

假设$h(k,\theta)$是在$h_1(k),h_2(k)$之间一个有能隙的,通常在$\theta\in[0,\pi],h(k,\theta)$不必要满足粒子空穴对称,对$\theta\in[\pi,2\pi]$定义

\[h(k,\theta)=-[C^{-1}h(-k,2\pi-\theta)C]^T\label{ha6}\]

选择这个参数化视为了当$\theta$被替换为高位空间中的动量波矢的时,哈密顿量满足粒子空穴对称。由于$h(k,\theta=0)$与$h(k,\theta=\pi)$的例子空穴对称,在$\theta\in[0,2\pi]$区间内$h(k,\theta)$是连续的,且$h(k,2\pi)=h(k,0)$。当$\theta$从0到$2\pi$进行绝热演化并对$h(k,\theta)$定义一个周期绝热泵浦,此时第一Chern数是定义在$(k,\theta)$空间中的,Chern数$C[h(k,\theta)]$可以表示成极化的winding number

\[C[h(k,\theta)]=\int d\theta\frac{\partial p(\theta)}{\partial\theta},\quad p(\theta)=\int\frac{dk}{2\pi}\sum_{E_\alpha(k)<0}(-i)\langle k,\theta;\alpha\rvert\partial_k\rvert k,\theta;\alpha\rangle\]

这里求和是对所有的占据态进行的。通常情况下两个不同的参数化$h(k,\theta),h^{‘}(k,\theta)$会对应着不同的Chern数$C[h(k,\theta)]\neq C[h^{‘}(k,\theta)]$,然而由对称限制(\ref{ha6})保证这两个不同的Chern数相差偶数$C[h(k,\theta)]-C[h^{‘}(k,\theta)]=2n,n\in Z$。

接下来证明上面的结论,对$h(k,\theta)$的本征态$\rvert k,\theta;\alpha\rangle$对应的本征值$E_\alpha(k,\theta)$,利用(\ref{ha6})可得

\[h(-k,2\pi-\theta)C\rvert k,\theta;\alpha\rangle^*=-E_\alpha(k)C\rvert k,\theta;\alpha\rangle^*\] \[\rvert k,\theta;\alpha\rangle^{*}=\sum_\beta(\langle m,\beta\rvert k,\theta;\alpha\rangle^*)\rvert m,\beta\rangle,\]

这里$m,\beta$分别是未知空间格点和轨道索引。因此$C\rvert k,\theta;\alpha\rangle^*\equiv\rvert -k,2\pi-\theta;\bar{\alpha}\rangle$是$h(-k,2\pi-\theta)$的本征态,对应的本征值为$E_{\bar{\alpha}}(k,2\pi-\theta)=-E_\alpha(k,\theta)$。哈密顿量$h(k,\theta)$与$h(-k,2\pi-\theta)$的本征态是一一对应的,从而可以得到

\[\begin{align} P(\theta)&=\int\frac{dk}{2\pi}\sum_{E_\alpha(k)<0}(-i)\langle k,\theta;\alpha\rvert\partial_k\rvert k,\theta;\alpha\rangle\nonumber\\ &=\int\frac{dk}{2\pi}\sum_{E_{\bar{\alpha}(-k)}>0}(-i)(\langle -k,2\pi-\theta;\bar{\alpha}\rvert)^*\cdot\partial_k\rvert -k,2\pi-\theta;\bar{\alpha}\rangle^*\nonumber\\ &=-P(2\pi-\theta)\label{ha7} \end{align}\]

因此$P(\theta)\quad\text{mod}\quad1$是well defined,(\ref{ha7})表明$P(\theta)+P(2\pi-\theta)=0\quad\text{mod}\quad 1$。对于$\theta=0$或者$\theta=\pi$有$2\pi-\theta=0\quad\text{mod}\quad 2\pi$,从而得到$P(\theta)=0\quad or\quad1/2$。也就是说极化取值为$1$或者$1/2$对任何满足粒子空穴对称的绝缘体。如果两个系统具有不同的极化P,在不破坏粒子空穴对称情况下,是不能通过绝热演化相互转换的,因为在绝热演化过程中P是个连续函数,当它不是0或者1/2时就破坏了粒子空穴对称。这也就解释了为什么在存在粒子空穴对称的情况下系统是$Z_2$分类的。有前面的定义可知极化$P(\theta)=\int dk a_k/2\pi$是规范依赖的,下面就来定义一个更加普遍的$Z_2$表达式,它仅包含规范不变量$\partial P(\theta)/\partial\theta$和Chern数$C_1$。

由对称性(\ref{ha7})可得

\[\begin{equation} \int^{\pi}_0dP(\theta)=\int_{\pi}^{2\pi}dP(\theta)\label{ha8} \end{equation}\]

它是规范独立的,因为只包含了极化$P(\theta)$的变化。这个方程表明在闭合路径的前半部分与后半部分极化的变化都是相同的。考虑两个不同的参数化过程$h(k,\theta),h^{‘}(k,\theta)$满足$h(k,0)=h^{‘}(k,0)=h_1(k),h(k,\pi)=h^{‘}(k,\pi)=h_2(k)$。这里$h(k,\theta),h^{‘}(k,\theta)$对应的极化分别为$P(\theta),P^{‘}(\theta)$,二者对应的Chern数之差为

\[C[h]-C[h^{'}]=\int_0^{2\pi}d\theta(\frac{\partial P(\theta)}{\partial\theta}-\frac{\partial P^{'}(\theta)}{\partial\theta})\]

定义新的差值$g_1(k,\theta),g_2(k,\theta)$

\[g_1(k,\theta)=\left\{\begin{array}{c}h(k,\theta),\quad\theta\in[0,\pi]\\h^{'}(k,2\pi-\theta),\quad\theta\in[\pi,2\pi]\end{array}\right. \\g_2(k,\theta)=\left\{\begin{array}{c}h^{'}(k,2\pi-\theta),\quad\theta\in[0,\pi]\\h(k,\theta),\quad\theta\in[\pi,2\pi]\end{array}\right.\]

这里$g_1(k,\theta)$与$g_2(k,\theta)$只是重新组合对两个路劲$h(k,\theta),h^{‘}(k,\theta)$进行了组合,如下图所示

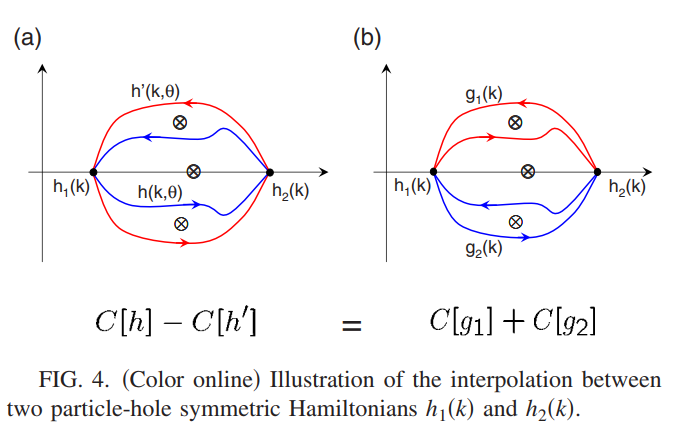
从$g_1,g_2$的构建路径可以直接得到

\[C[g_1]=\int_0^\pi d\theta(\frac{\partial P(\theta)}{\partial \theta}-\frac{\partial P^{'}(\theta)}{\partial\theta})\\ C[g_2]=\int^{2\pi}_\pi d\theta(\frac{\partial P(\theta)}{\partial\theta}-\frac{\partial P^{'}(\theta)}{\partial\theta})\]

因此可以得到$C[h]-C[h^{‘}]=C[g_1]+C[g_2]$,由(\ref{ha8})可以得到$C[g_1]=C[g_2]$,从而$C[h]-C[h^{‘}]=2C[g_1]$。由于$C[g_1]\in Z$我们可以得到$C[h]-C[h^{‘}]$的取值是偶数。Chern数$C[h],C[h^{‘}]$的不同是因为它们对应的路径之间存在奇异点,而且由于粒子空穴对称性的存在,这个奇异点的位置也是对称的。基于上面的讨论,可以定义一个相对Chern宇称

\[N_1[h_1(k),h_2(k)]=(-1)^{C[h(k,\theta)]}\]

它与$h(k,\theta)$的选取无关,只决定于哈密顿量$h_1(k),h_2(k)$。而且对于任意三个粒子空穴对称的哈密顿量$h_1(k),h_2(k),h_3(k)$总是满足

\[N_1[h_1(k),h_2(k)]N_1[h_2(k),h_3(k)]=N_1[h_1(k),h_3(k)]\]

由$N_1[h_1(k),h_2(k)]=1$在任意两个粒子空穴对称哈密顿量之间定义了一个等价关系,因此可以将所有满足粒子空穴对称的哈密顿量分成两类。定义一个真空态$h_0(k)\equiv h_0$,这里$h_0$是任意一个不依赖于动量$k$的矩阵且满足粒子空穴对称$C^\dagger h_0C=-h_0^T$,可以认为$h_0$描述的是一个没有hopping完全局域的系统,将它作为一个平庸的参考态可以得到$N_1[h_0(k),h_1(k)]\equiv N_1[h(k)]$作为哈密顿量$h(k)$的$Z_2$拓扑不变量。所有满足$N_1[h_0(k),h(k)]=1$的哈密顿量$h(k)$都是$Z_2$平庸的,满足$N_1[h_0(k),h(k)]=-1$的都是$Z_2$非平庸的。

对于一个$Z_2$非平庸的哈密顿量$h_1(k)$可以定义一个差值$h(k,\theta)$满足$h(k,0)=h_0,h(k,\pi)=h_1(k)$,对应的Chern数为$C[h(k,\theta)]$为奇整数,如果研究一个一维开边界的系统$h(k,\theta)$,实空间中的紧束缚哈密顿量为

\[h_{mn}(\theta)=\frac{1}{\sqrt{L}}\sum_ke^{ik(x_m-x_n)}h(k,\theta),\quad 1\leq m,n\leq L\]

此时再$h(k,\theta)$的能隙中有一个束缚态,与非零的Chern数相关联。当Chern数$C[h(k,\theta)]=2n-1,n\in Z$这里由一些值$\theta^L_s\in[0,2\pi),s=1,2,\cdots,2n-1$,此时哈密顿量$h_{mn}(\theta_s)$有零能的局域态在系统的左边界上,同样的有相同数目的零能态在有边界上其$\theta^R_s$与左端相同。

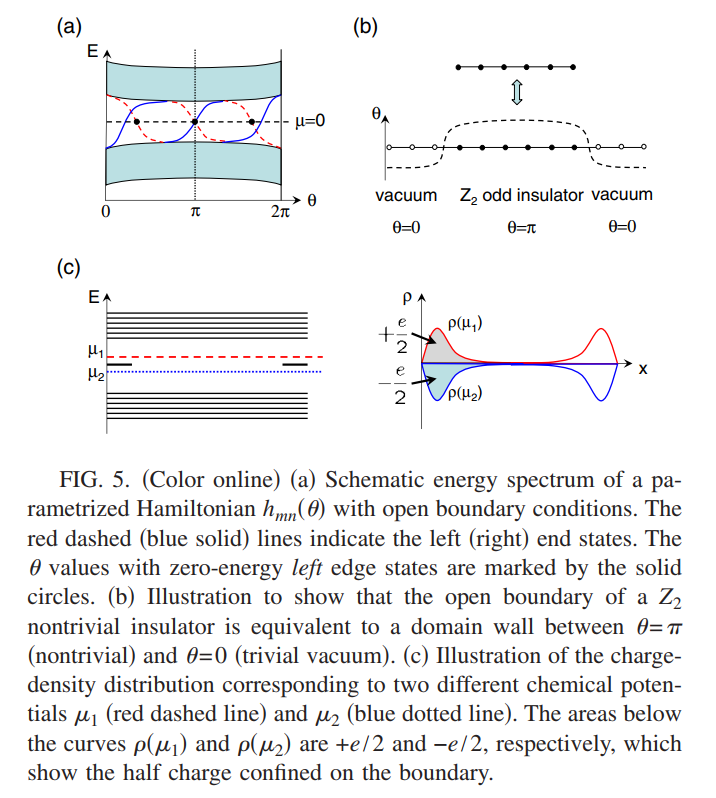
由于在$h_{mn}(\theta)$与$h_{mn}(2\pi-\theta)$之间有粒子空穴对称性的存在,零能态总是成对出现在$\theta$与$2\pi-\theta$处。当 Chern数是奇数是,一定有零能级出现在$\theta=0$和$\theta=\pi$。由于$\theta=0$是个平庸的绝缘体,对应着平带因此不存在终端态,局域的 零能拓扑态出现在$\theta=\pi$处。

总而言之,一个粒子空穴对称的$Z_2$拓扑绝缘体在开边界的时候会存在一个零能的局域态。

存在零能级会有一个重要的物理结果，在非平庸拓扑绝缘体边界上将会存在半整数的电荷，在周期系统中当化学势为零的时候，当有$N$条占据的能带时，每个格点上平均的粒子数密度为

\[\bar{n}_m=\langle\sum_\alpha c^\dagger_{m\alpha}c_{m\alpha}\rangle=N\]

在开放边界时相对于$N$的粒子数为$\rho_m(\mu)=\langle\sum_\alpha c^\dagger_{m\alpha}c_{m\alpha}\rangle_\mu-N$，粒子空穴对称性会保证$\rho_m(\mu)=-\rho_m(-\mu)$，当化学势$\mu$在能隙中间时，$\mu,-\mu$的区别就是零能态束缚在$\rvert 0L\rangle$还是$\rvert 0R\rangle$，对格点$m$足够远离右边界的时候

\[\text{lim}_{\mu\rightarrow 0^{+}}[\rho_m(\mu)-\rho_m(-\mu)]=\sum_\alpha\rvert\langle m\alpha\rvert 0L\rangle\rvert^2\]

当对左边界进行求和$\sum_m\rho_m(\mu\rightarrow 0^+)=1/2$，此时并不会包括另外一端的贡献。当零能态未被占据时边界上将会局域$1/2$个电子，当被占据时则会有$-1/2$个电子占据。从在半整数电荷也可以在开边界条件下，从非平庸于平庸相的质量畴壁视角来理解，通过对$h_{mn}(\theta)$定义插值，与空间依赖的畴壁为$\theta(x\rightarrow+\infty)=\pi,\theta(x\rightarrow-\infty)=0$，由相应公式(\ref{ha8})可得畴壁上积累的电荷为

\[Q_d=e\int_{-\infty}^{+\infty}dx\frac{\partial P[\theta(x)]}{\partial x}=e\int dP(\theta)=\frac{e}{2}\int_0^{2\pi}dP(\theta)=\frac{e}{2}C[h(k,\theta)]\]

这里需要强调，对于一个占据的局域态，其上面的电子总是可以变化整数个，也就是说$Q_d$只有$\text{mod}\quad e$才是有意义的，边界上存在分数的电荷$a\pm e/2$也仅仅在系统时拓扑非平庸的时候才满足。

(0+1)维$Z_2$分类粒子空穴对称绝缘体

对$(1+1)$维的系统进行围堵约化来研究$(0+1)$维系统的性质，这个维度约化的研究可以帮助理解后面$(2+1)$维时间反演不变(TRI)拓扑绝缘体从$(4+1)$维约化而来的过程。

自由粒子哈密顿量$h$满足粒子空穴对称表现为

\[C^\dagger hC=-h^T\]

给定两个满足粒子空穴对称的额哈密顿量$h_1,h_2$，利用和前面相同的处理过程在区间$\theta\in[0,2\pi]$定义连续插值$h(\theta)$满足

\[h(0)=h_1,\quad h(\pi)=h_2,\quad C^\dagger h(\theta)C=-h(2\pi-\theta)^T\label{ha9}\]

对所有的$\theta$而言$h(\theta)$都是有能隙的，哈密顿量$h(\theta)$是$(1+1)$维哈密顿量$h(k)$进行维度约化后的结果，此时波矢$k$被$\theta$代替。限制条件(\ref{ha9})正是粒子空穴对称性，所以$h(\theta)$就对应着满足粒子空穴对称的$(1+1)$维绝缘体，可以通过Chern宇称$N_1[h(\theta)]$来进行分类。如果$N_1[h(\theta)]=-1$，在哈密顿量$h(\theta)$与真空哈密顿量$h(\theta)=h_0,\theta\in[0,2\pi]$之间没有满足粒子空穴对称的连续插值存在。在$h_1,h_2$之间考虑两个不同的插值$h(\theta),h^{‘}(\theta)$，通过结合律

\[N_1[h(\theta)]N_1[h^{'}(\theta)]=N_1[h(\theta),h^{'}(\theta)]\]

它是两个插值路径的相对Chern宇称。因为$N_1[h(\theta)]$与$h_1,h_2$之间的插值是不相关的，所以$N_0[h_1,h_2]\equiv N_1[h(\theta)]$可以被定义为$h_1,h_2$的函数。此时$(0+1)维Z_2$量$N_0$与$(1+1)$维时候的$N_1[h(k),h^{‘}(\theta)]$扮演者相同的角色。

在$h(\theta),h^{‘}(\theta)$之间定义连续插值$g(\theta,\varphi)$，它满足

\[\begin{align} &g(\theta,\varphi=0)=h(\theta),\quad g(\theta,\varphi=\pi),h^{'}(\theta),\quad g(0,\varphi)=h_1,\\ &g(\pi,\varphi)=h_2,\quad C^\dagger g(\theta,\varphi)C=-g(2\pi-\theta,2\pi-\varphi)^T \end{align}\]

根据上一节的讨论可以简单的得到这样的连续插值总是可以存在的，对于所有的$\theta,\varphi$，函数$g(\theta,\varphi)$都是有能隙的。在两维参数空间$(\theta,\varphi)$中总是可以定义Berry位相和第一Chern数$C_1[g(\theta,\varphi)]$。通过定义Chern宇称可以得到$N_1[h(\theta),h^{‘}(\theta)]=(-1)^{C_1[g(\theta,\varphi)]}$。参数化的哈密顿量可以从两个视角来看：不仅在$h(\theta),h^{‘}(\theta)$间定义了插值，同样在$g(0,\varphi)=h_1,g(\pi,\varphi)=h_2$之间也定义了插值。无论$\varphi$去任何值，$g(0,\varphi),g(\pi,\varphi)$都是真空态哈密顿量，它们都有相对平庸的Chern宇称

\[N_1[h(\theta),h^{'}(\theta)]=N_1[g(0,\varphi),g(\pi,\varphi)]=N_1[h_1,h_2]=1\]

从上面的分析可以得到,任何两个属于相同$Z_2$类的$h(\theta)$与$h^{‘}(\theta)$,他们的Chern宇称$N_1[h(\theta)]$仅仅依赖于终点的$h_1,h_2$。也就是说$N_0[h_1,h_2]\equiv N_1[h(\theta)]$定义了一对粒子空穴对称哈密顿量$h_1,h_2$之间的关系。之后选择任意一个参考哈密顿量$h_0$,总是可以定义所有哈密顿量满足$N_0[h_0,h]=1$是平庸的$N_0[h_0,h]=-1$是非平庸的。此时与$(1+1)$维情况有所不同的是参考哈密顿量$h_0$的选择不是自然的。总而言之,平庸与非平庸仅仅在$(0+1)$维具有意义。但是分类仍然是有意义的,任意两个哈密顿量满足$N_0[h_1,h_2]=-1$都不能在不破坏粒子空穴对称的情况下绝热转换。单格点粒子空穴对称哈密顿量的流形是不连通的,起码会存在两个连接的片段。

考虑一个简单的$2\times 2$哈密顿量,通常单格点哈密顿量可以分解为

\[h=d_0\sigma^0+\sum_{a=1}^3d_a\sigma^a\]

当粒子空穴变换$C=\sigma^1$要求$C^\dagger hC=-h^T$时,从上面的表达式可以得到$d_0=d_1=d_2=0$,因此$h =d_3\sigma^3$,只要$d_3\neq 0$哈密顿量$h$就有能隙。下面来看$d_3>0,d_3<0$这两个简单的$Z_2$分类。先找到一个绝热的插值$h(\theta)=d_0(\theta)\sigma^0+\sum_ad_a(\theta)\sigma^a$是定义在$d_3>,d_3<0$之间,自旋矢量$\vec{d}(\theta)$可以会沿着有粒子空穴对称决定的虚拟路径从北极点向南极点演化。

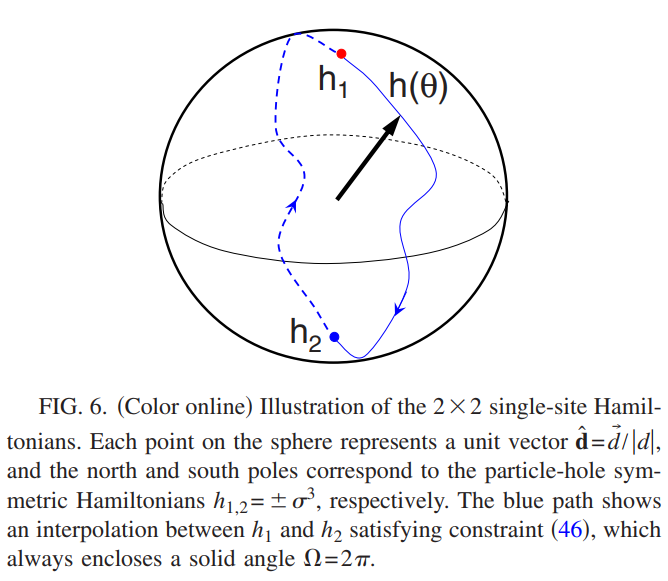
拓扑数$N_0[h_1,h_2]$可以简单的通过路径$d_a(\theta)$所包含的Berry位相来决定,当$h_1,h_2$在不同的极点是为$\pi$否则就是0。通过上面的例子就可以从图像上清晰的理解$Z_2$的含义。

第二Chern数及其物理结果

根据前面的维度约化,从时间反演破缺$(2+1)$维的拓扑绝缘体通过第一Chern数进行分类,进而得到了$(1+1)\rightarrow(0+1)$维的对应理论。这里利用相同的维度约化方式从$(4+1)\rightarrow(3+1)\rightarrow(2+1)$维的链式来研究时间反演不变的拓扑绝缘体。

$(4+1)$维中的第二Chern数及非线性响应

$(4+1)$维的绝缘体在外部$U(1)$规范场作用下会出现非线性响应,其系数对应着第二Chern数。它与前面$(2+1)$系统的Hall电导对应的第一Chern数是完全类似的。通过路径积分的方式来描述非线性响应是比较方便的,考虑一个耦合了$U(1)$规范场的$(4+1)$维哈密顿量

\[H[A]=\sum_{m,n}(c^\dagger_{m\alpha}h_{mn}^{\alpha\beta}e^{iA_{mn}}c_{n\beta}+\text{H.c})+\sum_mA_{0m}c^\dagger_{m\alpha}c_{m\alpha}\]

规范场$A^\mu$的有效作用量可以通过路径积分得到

\[e^{iS_\text{eff}[A]}=\int D[c]D[c^\dagger]\exp\{i\int dt[\sum_mc^\dagger_{m\alpha}(i\partial_t)c_{m\alpha}-H[A] \}=\text{det}[(i\partial_t-A_{0m})\delta^{\alpha\beta}_{mn}-h^{\alpha\beta}_{mn}e^{iA_{mn}}]\]

费米子系统的响应函数为

\[j_\mu({\bf x})=\frac{\delta S_\text{eff}[A]}{\delta A_\mu({\bf x})}\]

对于$(2+1)$维的情况,有效作用量$S_\text{eff}$包含了Chern-Simons项$(C_1/4\pi)A_\mu\epsilon^{\mu\nu\tau}\partial_\nu A_\tau$如公式(\ref{h2})所示,第一Chern数$C_1$出现在系数中。对于$(4+1)$维的系统,一个相似的拓扑项也会出现在有效作用量中,这就是第二Chern数

\[S_\text{eff}=\frac{C_2}{24\pi^2}\int d^4xdt\epsilon^{\mu\nu\rho\sigma\tau}A_\mu\partial_\nu A_\rho\partial_\sigma A_\tau\]

这里$\mu,\nu,\rho,\sigma,\tau=0,1,2,3,4$,这里的系数$C_2$可以通过计算单圈Feynamn图进行计算

\[C_2=-\frac{\pi^2}{15}\epsilon^{\mu\nu\rho\sigma\tau}\int\frac{d^4kd\omega}{(2\pi)^5}\text{Tr}[(G\frac{\partial G^{-1}}{\partial q^\mu})(G\frac{\partial G^{-1}}{\partial q^\nu})(G\frac{\partial G^{-1}}{\partial q^\rho})(G\frac{\partial G^{-1}}{\partial q^\sigma})(G\frac{\partial G^{-1}}{\partial q^\tau})]\label{ha10}\]

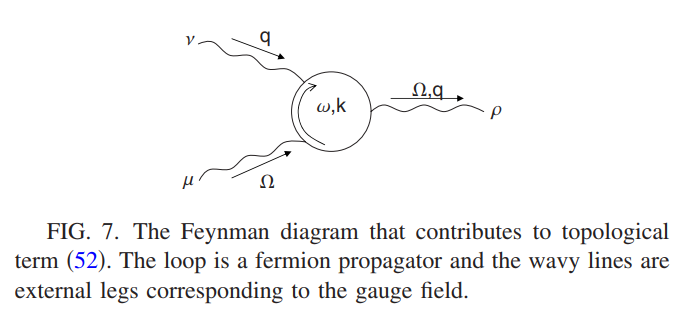
$q^\mu=(\omega,k_1,k_2,k_3,k_4)$是频率动量矢量,单粒子格林函数$G(q^\mu)=[\omega+i\delta-h(k_i)]^{-1}$。下面来研究第二Chern数$C_2$与非阿贝尔Berry位相规范场在动量空间中的联系。首先写出一些结论:

对于任何一个$(4+1)$维单粒子哈密顿量$h({\bf k})$的能带绝缘体,通过(\ref{ha10})定义的非线性响应系数$C_2$等于非阿贝尔Berry位相规范场在布里渊区(BZ)中的第二Chern数

\[C_2=\frac{1}{32\pi^2}\int d^4k\epsilon^{ijkl}\text{Tr}[f_{ij}f_{kl}],\quad f_{ij}^{\alpha\beta}=\partial_ia_j^{\alpha\beta}-\partial_ja_i^{\alpha\beta}+i[a_i,a_j]^{\alpha\beta},\quad a^{\alpha\beta}_i({\bf k})=-i\langle\alpha,{\bf k}\rvert\frac{\partial}{\partial k_i}\rvert\beta,{\bf k}\rangle\label{ha11}\]

这里$ij,k,l=1,2,3,4$。其中$a_i^{\alpha\beta}$中的$\alpha$是占据态的索引,因此对于一个一般的多带模型,$a_i^{\alpha\beta}$是个非阿贝尔规范场,$f_{ij}^{\alpha\beta}$与非阿贝尔场强相关联。这里的关键点是将(\ref{ha10})简化成一个拓扑不变量,不论哈密顿量发生怎样的变化,只要能带不穿过费米能级,那么$C_2$就是不变的。

先标记哈密顿量$h({\bf k})$的本征值$\epsilon_\alpha({\bf k}),\alpha=1,2,\cdots,N,\epsilon_\alpha({\bf k})\leq\epsilon_{\alpha+1}({\bf k})$。当有$M$条能带被占据的时候,从事可以对能带急性连续的形变$\epsilon_\alpha({\bf k})\rightarrow\epsilon_G$ for $\alpha\leq M,\epsilon_\alpha({\bf k})\rightarrow\epsilon_E$ for $\alpha>M,(\epsilon_E>\epsilon_G)$。 在变形的过程中,对应的所有本征态$\rvert\alpha,{\bf k}\rangle$都是不变的,也就是说可以把哈密顿量$h({\bf k})$变成一些平带模型。

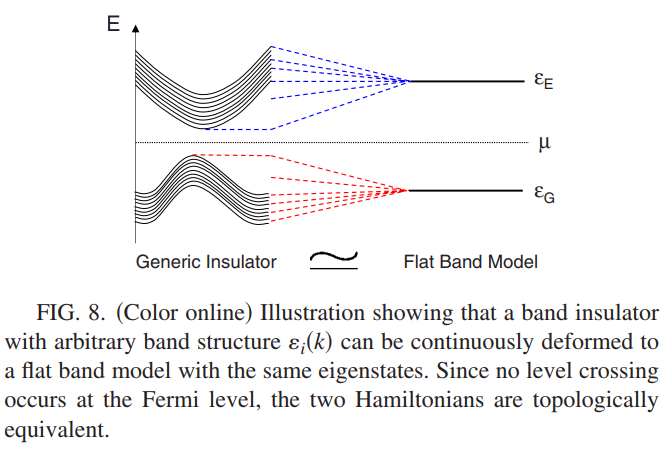
由于(\ref{ha10})与第二Chern数(\ref{ha11})都是拓扑不变量,下面对(\ref{ha11})研究其在平带上的性质,此时可以将哈密顿量写为

\[h_0({\bf k})=\epsilon_G\sum_{1\leq\alpha\leq M}\rvert\alpha,{\bf k}\rangle\langle\alpha,{\bf k}\rvert+\epsilon_E\sum_{\beta>M}\rvert\beta,{\bf k}\rangle\langle\beta,{\bf k}\rvert\equiv\epsilon_GP_G({\bf k})+\epsilon_EP_E({\bf k})\]

这里$P_G({\bf k})[P_E({\bf k})]$是占据态(空态)的投影算子。课题通过这些投影算子来定义非阿贝尔Berry联络,单粒子格林函数也可以通过投影算子来计算计算。综上可得,对于任意一个$(4+1)$维的能带绝缘体,这里总会有一个耦合$U(1)$规范场的有效作用量对应的Chern-Simons项,它的系数对应的正是非阿贝尔Berry位相规范场对应的第二Chern数。利用运动方程可以得到

\[j^\mu=\frac{C_2}{8\pi^2}\epsilon^{\mu\nu\rho\sigma\tau}\partial_\nu A_\rho\partial_\sigma A_\tau\label{ha12}\]

这是对外场$A_\mu$的非线性响应。当考虑下面的场时

\[A_x=0,A_y=B_zx,A_z=-E_zt,A_w=A_t=0\label{ha16}\]

这里$x,y,z,w$表示空间维度,$t$代表时间。非零分量的的场强度为$F_{xy}=B_z,F_{zt}=-E_z$,有(\ref{ha12})得到的电流为

\[j_w=\frac{C_2}{4\pi^2}B_zE_z\]

当沿着$x,y$方向进行积分之后(取周期边界条件且$E_z$不随$(x,y)$变化),可以得到

\[\int dxdyj_w=\frac{C_2}{4\pi^2}(\int dxdyB_z)E_z\equiv\frac{C_2N_{xy}}2\pi{E_z},\]

这里$N_{xy}=\int dxdy B_z/2\pi$是穿过$xy$平面的量子通量数目,这就是4D量子霍尔效应。第二Chern数为$C_2$的$(4+1)$维绝缘体,$zw$面上的量子Hall电导为$C_2N_{xy}/2\pi$,是由$xy$面上磁场磁通$2\pi N_{xy}$诱导出来的。第二Chern数同样可以通过研究表面态来理解,此时$(4+1)$维的表面态由$(3+1)$维的理论来描述。

基于Dirac模型的时间反演不变绝缘体

$(4+1)$维连续Dirac模型为

\[H=\int d^4 x[\psi^\dagger(x)\Gamma^i(-i\partial_i)\psi(x)+m\psi^\dagger\Gamma^0\psi],\quad i=1,2,3,4\text{是空间维度}\]

$\Gamma^\mu,\mu=0,1,2,3,4$是满足Clifford代数的Dirac矩阵

\[\{\Gamma^\mu,\Gamma^\nu\}=2\delta_{\mu\nu}\mathbb{I},\quad\mathbb{I}\text{是单位矩阵}\]

这个模型的格点形式为

\[H=\sum_{n,i}[\psi^\dagger_n(\frac{c\Gamma^--i\Gamma^i}{2})\psi_{n+\hat{i}}+\text{H.c}]+m\sum_n\psi^\dagger_n\Gamma^0\psi_n\label{ha15}\]

在动量空间中

\[H=\sum_{\bf k}\psi^\dagger_{\bf k}[\sum_i\sin k_i\Gamma^i+(m+c\sum_i\cos k_i)\Gamma^0]\psi_{\bf k}\label{ha13}\]

将哈密顿量写成更紧凑的形式

\[H=\sum_{\bf k}\psi^\dagger_{\bf k}d_a({\bf k})\Gamma^a\psi_{\bf k},\quad d_a({\bf k})=[(m+c\sum_i\cos k_i),\sin k_x,\sin k_y,\sin k_z,\sin k_w]\]

与之前研究$(2+1)$维两带模型相似,单粒子哈密顿量形式为$h({\bf k})=d_a({\bf k})\Gamma^a$由两个本征值$E_{\pm}-\pm\sqrt{\sum_ad_a^2({\bf k})}$,不过此时能级是二重简并的,当$\sum_ad^2a({\bf k})\equiv d^2({\bf k})$在整个BZ中不消失的时候,半满时系统是有能隙的,此时$E=E{-}$的能带是占据的。因为此时有两个占据的能带,可以定义一个$SU(2)\times U(1)$的绝热联络。从哈密顿量(\ref{ha13})可以定义单粒子格林函数并计算第二Chern数

\[C_2=\frac{3}{8\pi^2}\int d^4k\epsilon^{abcde}\hat{d_a}\partial_x\hat{d_b}\partial_y\hat{d_c}\partial_z\hat{d_w}\partial_e\label{ha14}\]

这是一个从BZ $T^4$到球$S^4$的映射,$\hat{d_a}({\bf k})\equiv d_a({\bf k})/\rvert d({\bf k})\rvert$。由(\ref{ha14})所表示的winding number等于Berry位相规范场对应的第二Chern数。对于格点模型(\ref{ha15})可以简单计算其$C_2$。考虑格点模型有固定的正参数$c$和一个可调参数$m$,随着$m$的变化Chern数$C_2(m)$就是关于$m$的函数。当哈密顿量是无能隙的时候,Chern数就会发生变化$\sum_ad_a^2({\bf k})=0$。当$m\rightarrow+\infty$是矢量$\hat{d_a}({\bf k})=(1,0,0,0,0)$此时的$C_2(m)=0$。因此只需要研究$C_2(m)$发生变化的量子临界点即可,也就是$C_2(m)$发生变化时$m$的值。通过$\sum_ad_a^2({\bf k})=0$可以求解得到临界值$m$和对应的动量点${\bf k}$

\[m=\left\{\begin{array}{c}-4,\quad{\bf k}=(0,0,0,0)\\ -2c,\quad {\bf k}\in P[(\pi,0,0,0)]\\ 0,\quad\mathbf{k}\in P[(\pi,0,\pi,0)]\\ 2c,\quad \mathbf{k}\in P[(\pi,\pi,\pi,0)]\\ 4c,\quad\mathbf{k}=(\pi,\pi,\pi,\pi)\end{array}\right.\]

这里$P[\mathbf{k}]$表示通过交换波矢的索引得到的一系列矢量$\mathbf{k}$。比如$P[(\pi,0,0,0)]$包含了$(\pi,0,0,0),(0,\pi,0,0),(0,0,\pi,0),(0,0,0,\pi)$。下面研究一下临界点$m=-4c$处第二Chern数$C_2(m)$的变化。在$m+4c«2c$的极限下,系统最小能隙位于$\mathbf{k}=0$,在该点进行低能展开可得$d_a({\bf k})\simeq (\delta m,k_x,k_y,k_z,k_w)+o(\rvert k\rvert),\delta m\equiv m+4c$。在动量空间中做截断$\Lambda«2\pi$,可以得到第二Chern数在低能和高能部分

\[C_2=\frac{3}{8\pi^2}(\int_{\rvert\mathbf{k}\rvert<<\Lambda}+\int_{\rvert\mathbf{k}\rvert>>\Lambda})\epsilon^{abcde}\hat{d}_a\partial_x\hat{d}_b\partial_y\hat{d}_c\partial_z\hat{d}_d\partial_w\equiv C_2^{(1)}(\delta m,\Lambda)+C_2^{(2)}()\delta m,\Lambda\]

因为在高能部分$\rvert\mathbf{k}\rvert>\Lambda$不存在能级交叉,所以$C_2$在$\delta m=0$处的跃变仅仅来源于$C_2^{(1)}$,在极限$\rvert\delta m\rvert<\Lambda«2\pi$时,通过连续近似的$d_a(\mathbf{k})$可得到

\[C_2^{(1)}(\delta m,\Lambda)\simeq\frac{3}{8\pi^2}\int_{\rvert\mathbf{k}\rvert<<\Lambda}d^4k\frac{\delta m}{(\delta m^2+\mathbf{k}^2)^{5/2}}\]

通过积分可以得到

\[\Delta C_{2\delta m=0^-}^{\delta m=0^+}=\Delta C_{2\delta m=0^-}^{(1)\delta m=0^+}=1\]

从上面的分析可以知道第二Chern数由在能级交叉处有效连续模型来决定,在连续模型情况下对应的正是Dirac 模型。对所有临界点附近进行分析可以得到

\[C_2(m)=\left\{\begin{array}{c}0,\quad m<-4c\quad\text{or}\quad m>4c\\ 1,\quad -4c<m<-2c\\ -3,\quad -2c<m<0\\ 3,\quad 0<m<2c\\ -1,\quad 2c<m<4c\end{array}\right.\]

在得到了第二Chern数之后,就可以通过拓扑非平庸的表面态来研究这个模型,与前面的研究方法相同,沿某一个方向取开边界,比如取$w$方向,其余的维度都是周期边界条件,哈密顿量可以转换成一个1D紧束缚模型的求和

\[H=\sum_{\vec{k},w}[\psi^\dagger_{\vec{k}}(w)(\frac{c\Gamma^0-i\Gamma^4}{2})\psi_{\vec{k}}(w+1)+\text{H.c}]+\sum_{\vec{k},w}\psi^\dagger_{\vec{k}}(w)[\sin k_i\Gamma^i+(m+c\sum_i\cos k_i)\Gamma^0]\psi_\vec{k}(w)\]

$C_2\neq 0$的能隙间表面态如下图所示

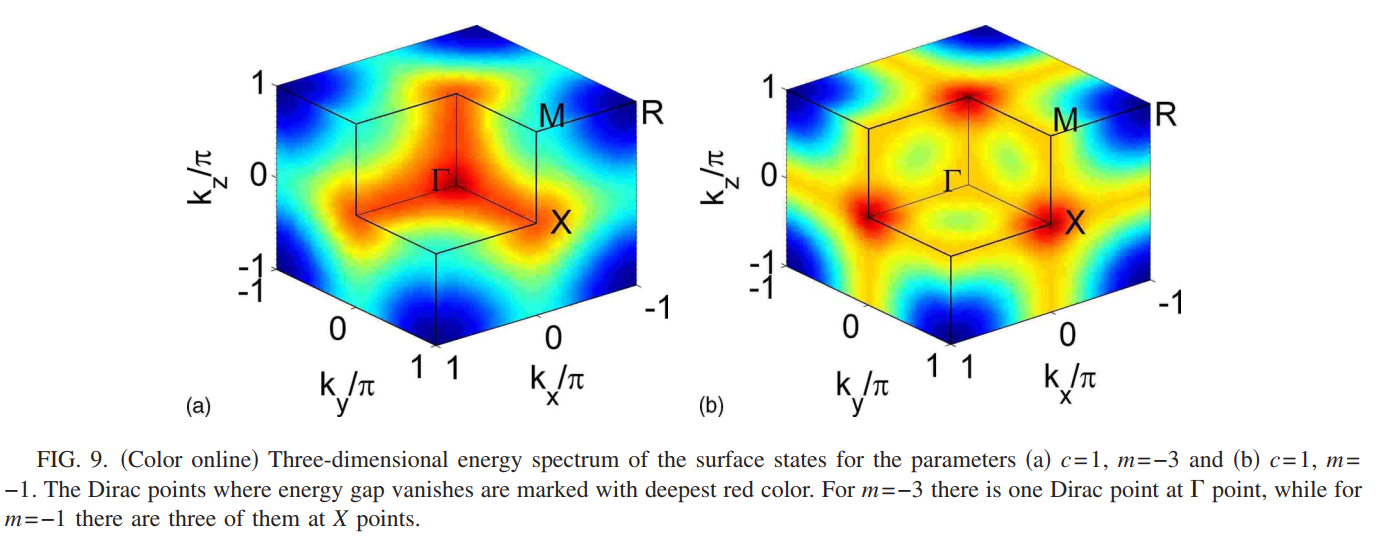
当Chern数是$C_2$时,这里会有$C_2$支线性色散无能隙的表面态,其低能有效理论可以通过有$\rvert C_2\rvert$个手性费米子

\[H=\text{sgn}(C_2)\int\frac{d^3 p}{(2\pi)^3}\sum_{i=1}^{\rvert C_2\rvert}v_i\psi^\dagger_i(\vec{p})\vec{\sigma}\cdot\vec{\mathbf{p}}\psi_i(\vec{p})\]

前面的因子$\text{sgn}(C_2)$保证了表面态的手性,是由Chern数的符号决定的。从表面理论可以从更加物理的角度来理解外场$U(1)$规范场与非线性响应之间的关联。k考虑与(\ref{ha16})相同的规范场构型,则非零的场曲率为$F_{xy}=b_z,F_{zt}=-E_z$。最终一个$(3+1)$维表面态耦合磁场$\mathbf{B}=B_z\hat{\mathbf{z}}$和电场$\mathbf{E}=E_z\hat{\mathbf{z}}$,此时考虑$-4c<m<-2c$这个参数区间,对应的$cC_2=1$,此时的表面理论是手性费米子的单粒子哈密顿量

\[h=v\vec{\sigma}\cdot(\vec{p}+\vec{A})=v\sigma_xp_x+v\sigma_y(p_y+B_zx)+v\sigma_z(p_z-E_zt)\]

如果$E_z$足够小,此时时间依赖项$A_z(t)=-E_zt$可以看做是微扰,当$A_z$固定的时候单粒子能谱为

\[E_{n\pm}(p_z)=\pm v\sqrt{(p_z+A_z)^2+2n\rvert B_z\rvert},n=1,2,\cdots,\quad E_0(p_z)=v(p_z+A_z)\text{sgn}(B_z)\]

当表面取$L_x\times L_y\times L_z$的周期边界条件时,每个朗道能级的简并度为$N_{xy}=L_xL_yB_z/2\pi$。与量子Hall边界态的规范讨论相似,无限小的电场$E_z$将会绝热的移动动量$p_z\rightarrow p_z+E_zt$,如下图所示,从$t=0$到$t=T\equiv 2\pi/L_zE_z$时,动量的变化为$p\rightarrow p_z+2\pi/L_z$,此时3D表面上净增加的电子数目为$N_{xy}$,总而言之,一个一般的Hall流$I_w$个是沿着$w$方向的

\[I_w=\frac{N_xy}{T}=\frac{L_xL_yL_zB_zE_z}{4\pi^2}\]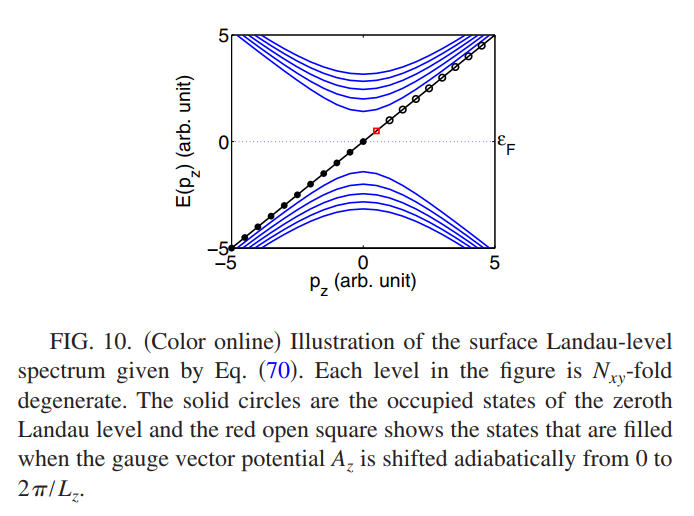

根据电流密度可以得到$j_w=B_zE_z/4\pi^2$,这与前面得到的结果(\ref{ha12})一致。更加一般形式的电流密度$j_w$可以表示为

\[j_w=C_2\frac{\mathbf{E}\cdot\mathbf{B}}{4\pi^2}=\frac{C_2}{32\pi^2}\epsilon^{\mu\nu\sigma\tau}F_{\mu\nu}F_{\sigma\tau}\]

这是无质量$(3+1)$维Dirac费米子的手性反常方程。因为4D格点Dirac模型的3D无能隙边界态是手性费米子,所以电流$I_w$总是包含着特定手性的电荷,这将会导致3D边界上手性不守恒。

维度约化$(3+1)$维时间反演不变绝缘体

对于满足时间反演不变(TRI)的$(4+1)$维的体系其第二Chern数不为零,通过将其中的某个动量参数替换成$\theta$来实现维度约化的目的,从而可以来研究$(3+1)$维以及$(2+1)$维绝缘体。

$(3+1)$维绝缘体的有效作用量

Dirac哈密顿量(\ref{ha15})耦合外部$U(1)$规范场之后

\[H[A]=\sum_{n,i}[\psi^\dagger_n(\frac{c\Gamma^0-i\Gamma^i}{2})e^{iA_{n,n+\hat{i}}}\psi_{n+\hat{i}}+\text{H.c}]+m\sum_n\psi^\dagger_n\Gamma^0\psi_n\]

现在考虑一个特殊的朗道规范$A_{n,n+\hat{i}}=A_{n+\hat{w},n+\hat{w}+\hat{i}}$,它沿着$w$方向是平移不变的,因此在周期边界条件下$w$方向的动量$k_w$是个好量子数,哈密顿量可以写为

\[\begin{align}H[A]&=\sum_{k_w,\vec{x},s}[\psi^\dagger_{\vec{x},k_w}(\frac{c\Gamma^0-i\Gamma^s}{2})e^{iA_{\vec{x},\vec{x}+\hat{s}}}\psi_{\vec{x}+\hat{s},k_w}+\text{H.c}]\\ &+\sum_{k_w,\vec{x},s}\psi^\dagger_{\vec{x},k_w}\{\sin(k_w+A_{\vec{x}4})\Gamma^4\\ &+[m+c\cos(k_w+A_{\vec{x}4})]\Gamma^0\}\psi_{\vec{x},k_w}\end{align}\]

这里的$\vec{x}$代表三维坐标,$A_{\vec{x}4}\equiv A_{\vec{x},\vec{x}+\hat{w}},s=1,2,3$表示$x,y,z$方向。在这个表达式中,不同$k_w$态是无耦合的,此时就可以将$(4+1)$的$H[A]$约化为一系列$(3+1)$维固定$k_w$的哈密顿量,重新改写$k_w + A_{\vec{x}4 =\theta_\vec{x}$约化到$(3+1)$维的模型为

\[H_{3D}[A,\theta]=\sum_{\vec{x},s}[\psi^\dagger_\vec{x}(\frac{c\Gamma^0-i\Gamma^s}{2})e^{iA_{\vec{x},\vec{x}+\hat{s}}}+\text{H.c}]+\sum_{\vec{x},s}\psi^\dagger_\vec{x}[\sin \theta_\vec{x}\Gamma^4+(m+c\cos \theta_\vec{x})\Gamma^0]\psi_\vec{x}\label{ha20}\]

着描述的是耦合电磁想$A_{\vec{x},\vec{x}+\hat{s}}$的能带绝缘体,绝热参数场为$\theta_\vec{x}$。为了研究$(3+1)$维系统的响应性质，有效作用量$S_\text{3D}[A,\theta]$为

\[\exp^{iS_\text{3D}[A,\theta]}=\int D[\psi]D[\bar{\psi}]\exp\{i\int dt[\sum_\vec{x}^{'}\bar{\psi}\vec{x}(i\partial_\tau-A_{\vec{x}0})\psi_\vec{x}-H[A,\theta]]\}\label{ha17}\]

在场构型$A_s(\vec{x},t)\equiv 0,\theta(\vec{x},t)\equiv\theta_0$处进行Taylor展开，$S_\text{3D}$中将会包含从$(4+1)$维推到得到的非线性响应

\[S_\text{3D}=\frac{G_3(\theta)}{4\pi}\int d^3xdt\epsilon^{\mu\nu\sigma\tau}\delta\theta\partial_\mu A_\nu\partial_\sigma A_\tau\label{ha18}\]

与(\ref{ha11})相比较，$\delta\theta(\vec{x},t)=\theta(\vec{x},t)-\theta_0$扮演了$A_4$的角色，系数$C_3(\theta)$可以通过相同的Feymann图来计算得到，只是此时需要对3D的哈密顿量(\ref{ha17})进行，不对$k_w$积分，最终可以得到$G_3(\theta)$的表达式

\[G_3(\theta)=-\frac{\pi}{6}\int \frac{d^3kd\omega}{(2\pi)^4}\text{Tr}\epsilon^{\mu\nu\sigma\tau}[(G\frac{\partial G^{-1}}{\partial q^\mu})(G\frac{\partial G^{-1}}{\partial q^\nu})(G\frac{\partial G^{-1}}{\partial q^\sigma})(G\frac{\partial G^{-1}}{\partial q^\tau})],\quad q^\mu=(\omega,k_x,k_y,k_z)\]

$G_3(\theta)$可以从Berry曲率中计算得到

\[G_3(\theta_0)=\frac{1}{8\pi^2}\int d^3k\epsilon^{ijk}\text{Tr}[f_{\theta i}f_{jk}]\]

此时Berry曲率是定义在四维空间中的$(k_x,k_y,k_z,k_\theta)$中，

\[a^{\alpha\beta}_i=-i\langle\vec{k},\theta_0;\alpha\rvert(\partial/\partial k_i)\rvert\vec{k},\theta_0;\beta\rangle,\quad a^{\alpha\beta}_\theta=-i\langle\vec{k},\theta_0;\alpha\rvert(\partial/\partial\theta_0)\rvert\vec{k},\theta_0;\beta\rangle\]

跟第二Chern数相比，可以得到求和规则

\[G_3(\theta)d\theta=C_2\in Z\]

这正好对应着$(1+1)$维系统中泵浦系数求和$G_1(\theta)$，前面$G_1(\theta)=\partial P_1/\partial\theta$，这里$P_1$就是简单的电子极化。同样的在$(3+1)$维同样可以定义广义极化$P_3(\theta)$满足$G_3(\theta)=\partial P_3/\partial\theta_0$。通常情况下电子极化$\mathbf{P}$是与外部电场$\mathbf{E}$线性耦合的，磁化$\mathbf{M}$与外部磁场$\mathbf{B}$也是线性耦合的，然而此时可以看到$P_3$是一个赝标量，它与外部电磁场$\mathbf{E}\cdot\mathbf{B}$是非线性耦合的，因为这个原因通常称$P_3$是磁电极化。

为了得到$P_3$需要介绍非阿贝尔Chern-Simons项

\[\mathcal{K}^A=\frac{1}{16\pi^2}\epsilon^{ABCD}\text{Tr}[(f_{BC}-\frac{1}{3}[a_B,a_C])\cdot a_D]\]

这是一个四维空间$q=(k_x,k_y,k_z,\theta_0)$中的矢量，$A,B,C,D=x,y,z,\theta$，$\mathcal{K}$满足

\[\partial_A\mathcal{K}=\frac{1}{32\pi^2}\epsilon^{ABCD}\text{Tr}[f_{AB}f_{CD}]\rightarrow G_3(\theta_0)=\int d^3k\partial_A\mathcal{K}\]

当第二Chern数等于0时，在定义$a_A$的时候会遇到阻塞，也就意味在整个参数空间中$\mathcal{K}$不是单值的，然而在一个合适的规范选择下$\mathcal{K}$可以时单值的，$G_3(\theta)=\int d^3\partial_\theta\mathcal{K}^\theta\equiv\partial P_3(\theta_0)/\partial\theta_0$

\[P_3(\theta_0)=\int d^3k\mathcal{K}^\theta=\frac{1}{16\pi^2}\int d^3k\epsilon^{\theta ijk}\text{Tr}[(f_{ij}-\frac{1}{3}[a_i,a_j])\cdot a_k]\]

因此$P_3(\theta)$时非阿贝尔Chern-Simons项在三分量动量空间中的积分。这与电子极化时定义在一个动量空间中绝热演化路径的积分时相似的。

众所周知，Chern-Simons在三维的积分只有对整数取模才是规范不变的，在一个规范变换$a_i\rightarrow u^{-1}a_iu-iu^{-1}$下，极化$P_3$的改变为

\[\Delta P_3=\frac{i}{24\pi^2}\int d^k \epsilon^{theta ijk}\text{Tr}[(u^{-1}\partial_i u)(u^{-1}\partial_j u)(u^{-1}\partial_k u)]\]

它是一个整数，因此$P_3$就像$P_1$一样对1取模才是well defined，当改变$\theta_0$从0到$2\pi$就可以得到$C_2$。有效作用量(\ref{ha18})可以通过引入$G_3=\partial P_3/\partial\theta$进行简化，然后进行分部积分之后

\[S_{3D}=\frac{1}{4\pi}\int d^3kdt\epsilon^{\mu\nu\sigma\tau}A_\mu(\partial P_3/\partial\theta)v_\nu\delta\theta\partial_\sigma A_\tau\label{ha19}\]

这个有效的作用量对任意绝热依赖于$\vec{x},t$的哈密顿量$h(\vec{k},\vec{x},t)$都是well defined。这个有效作用量在场论中被称为轴子电动力学,绝热场$P_3$扮演了轴子场的作用。

有效作用量$S_{3D}$的物理效应

有效作用量是$A_\mu$的二次型,他描述了对外部电磁场的线性响应,而且这个场同时依赖于空间和$P_3$对时间的梯度。对$S_{3D}$求变分可以得到响应方程

\[j^\mu=\frac{1}{2\pi}\epsilon^{\mu\nu\sigma\tau}\partial_\nu P_3\partial_\sigma A_\tau\label{ha21}\]

下面可以从两种情况来理解上式的结果

空间梯度$P_3$诱导Hall效应

卡片绿亦歌系统$P_3=P_3(z)$仅在$z$方向变化,这个可以通过在Dirac模型(\ref{ha20})中变化$\theta=\theta(z)$,在这种情况下(\ref{ha21})变成

\[j^\mu=\frac{\partial_z P_3}{2\pi}\epsilon^{\mu\nu\rho}\partial_\nu A_\rho,\quad\mu,\nu,\rho=t,x,y\]

它描述了在$xy$平面上的量子霍尔效应,对应的Hall电导为$\sigma_{xy}=\partial_zP_z/2\pi$,如下图所示

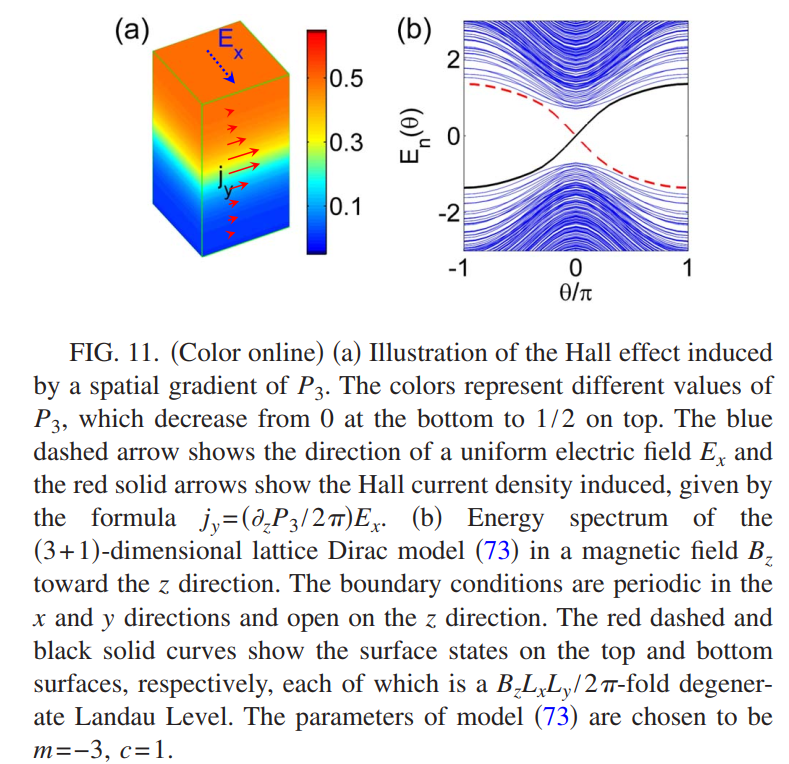
对于一个在$x$方向均匀的电场$E_x$,Hall电流密度$j_y=(\partial_z P_3/2\pi)E_x$。沿着$z$方向有限区间急性积分就可以得到$xy$上的电流密度

\[J^{2D}_y=\int_{z_1}^{z_2}dzj_y=\frac{1}{2\pi}(\int_{z_1}^{z_2}dP_3)E_x\]

在区间$z_1\leq z\leq z_2$内的净Hall电导为

\[\sigma_{xy}^{2D}=\int_{z_1}^{z_2}dP_3/2\pi\]

在这个区间内它仅依赖于$P_3$的变化,与不依赖于其具体的细节$P_3(z)$。与$(1+1)$维的情况相似,如果对(\ref{ha8})进行空间积分,就可以得到由极化诱导出来的总电荷

$Q=-\int_{z_1}^{z_2}dP/2\pi$

通过比较可以发现在$(3+1)$维中的$P_3$与Hall电导间的关系与$(1+1)$维中极化与总电荷之间的关系式类似的。两个均匀材料将不同$P_3$处将会琮琤畴壁,从而由Hall电导为$\sigma_H=\Delta P_3/2\pi$。在$(1+1)$维中诱导的分数电荷为$Q=-\Delta P/2\pi$。

$P_3$时间梯度诱导的拓扑磁电效应

当$P_3=P_3(t)$是空间均匀,但随着时间变化时,

\[j^i=-\frac{\partial_t P_3}{2\pi}\epsilon^{ijk}\partial_jA_k,\quad i,j,k=x,y,z,\quad\vec{j}=-\frac{\partial_tP_3}{2\pi}\vec{B}\label{ha22}\]

由于电荷极化$\vec{P}$满足$\vec{j}=\partial_t\vec{P}$,对于一个静态均匀的磁场B可以得到$\partial_t\vec{P}=-\partial_t(P_3\vec{B}/2\pi)$,因此有

\[\vec{P}=-\frac{\vec{B}}{2\pi}(P_3+\text{const})\]

这个方程描述了有磁场诱导的电子极化,正是磁电效应。与多铁材料中相同的效应相比较,此时的磁电效应是拓扑起源仅仅依赖于磁电极化$P_3$。与$(1+1)$维绝热泵浦效应相似,响应同样可以从表面态物理来理解,考虑一个格点Dirac模型(\ref{ha20})沿$x,y$方向是周期的$z$方向是开边界,当存在沿$z$方向的静态磁场$B_z$时,单粒子的能谱$E_n(\theta)$可以在固定$\theta$出进行求解,如上图(b)所示,在$(2+1)$维的边界上存在midgap states。 这里需要注意的是每个态都是$N$重简并的,$N=B_zL_xL_y/2\pi$是朗道能级简并度,在格点模型中当$-4c<m<-2c$时第二Chern数$C_2=\int^{\theta=2\pi}_{\theta=0}dP_3=1$可以发现在一个周期中$\theta=0\rightarrow2\pi$,$N$重简并的表面态在下边界下沉,然后再上边界浮出,当$\theta$绝热的从$0$到$2\pi$的过程中,将会有$N$个电子从上表面泵浦到下表面,这与前面(\ref{ha22})的结果是一致的

\[\Delta Q=\int dt\int dxdyj_z=-\frac{\int_0^{2\pi}dP_3}{2\pi}B_zL_xL_y=-NC_2\]

在$(3+1)$维系统中磁场的绝热泵浦是$(4+1)$维拓扑绝缘体表面手性反常诱导的。当磁单极存在的时候,拓扑词典效应将会存在特异的性质,对于一个均匀的$P_3$,方程(\ref{ha22})推导出

\[\nabla\cdot\vec{j}=-\frac{\partial_tP_3}{2\pi}\nabla\cdot\vec{B}\]

在格点上考虑紧致的$U(1)$电磁场,磁单极密度为$\rho_m=\nabla\cdot\vec{B}/2\pi$可以是非零的,可以得到

\[\partial_t\rho_e=(\partial_tP_3)\rho_m\]

因此当$P_3$绝热的从0变话到$\Theta/2\pi$,磁单极会获得一个电荷

\[Q_e=\frac{\Theta}{2\pi}Q_m\]

$Z_2$分类的时间反演不变绝缘体

在前面分析$(1+1)$维粒子空穴对称绝缘体中,关键是要找到两个满足粒子空穴对称的差值$h_1(k),h_2(k)$具有相同的Chern数宇称,这样他们相对Chern宇称就是well defined。此时3D系统具有的是时间反演对称,它会扮演与粒子空穴对称相同的作用。对于一个哈密顿量

\[H=\sum_{mn}c^\dagger_{m\alpha}h^{\alpha\beta}_{mn}c_{n\beta}\]

对应的时间反演变化时个反幺正算符$c_{m\alpha}\rightarrow T^{\alpha\beta}c_{m\beta}$,这里时间反演矩阵$T$满足$T^\dagger T=\mathbb{I},T^*T=-\mathbb{I}$,在动量空间中时间反演对称要求

\[T^\dagger h(-\vec{k})T=h^T(\vec{k})\]

$T^*T=-\mathbb{I}$是重要的,它将会导致Kramers简并,现在利用与前面$(1+1)$维相同的方法来对$(3+1)$维TRI的系统定义$Z_2$不变量。对任意两个TRI的能带绝缘体$h_1(k),h_2(k)$,可以定义插值$h(k,\theta)$满足

\[h(k,0)=h_1(k),\quad h(k,\pi)=h_2(k),\quad T^\dagger h(-k,-\theta)T=h^T(k,\theta)\]

腿与$\theta\in [0,2\pi],h(k,\theta)$都是有能隙的。因为插值是$\theta$的周期函数,那么可以在$(k,\theta)$空间中定义Berry位相规范场的第二Chern数$C_2[h(k,\theta)]$。下面来研究对于任意两个插值$h,h^{‘}$其$C_2[h(k,\theta)]-C_2[h^{‘}(k,\theta)]=0\quad\text{mod}\quad 2$。定一辆个新的$g_{1,2}(k,\theta)$

\[g_1(k,\theta)=\left\{\begin{array}{c}h(k,\theta),\quad\theta\in [0,\pi]\\ h^{'}(k,2\pi-\theta),\quad\theta\in[\pi,2\pi]\end{array}\right. \\ g_2(k,\theta)=\left\{\begin{array}{c}h^{'}(k,2\pi-\theta),\quad\theta\in [0,\pi]\\ h(k,\theta),\quad\theta\in[\pi,2\pi]\end{array}\right.\]

通过定义,$g_1,g_2$满足$C_2[h]-C_2[h^{‘}]=C_2[g_1]+C_2[g_2],T^\dagger g_1(-k,-\theta)T=g_2^T(k,\theta)$。为了研究$C_2[g_1]=C_2[g_2]$考虑$g_1(k,\theta)$的本征值为$E_\alpha(k,\theta)$的本征态$\rvert k,\theta;\alpha\rangle_1$

\[g_2^T(-k,-\theta)T^\dagger\rvert k,\theta;\alpha\rangle_1=T^\dagger g_1(k,\theta)\rvert k,\theta;\alpha\rangle_1=E_\alpha(k,\theta)T^\dagger\rvert k,\theta;\alpha\rangle_1\\ \rightarrow g_2(-k,-\theta)T^T(\rvert k,\theta;\alpha\rangle_1)^*=E_\alpha(k,\theta)T^T(\rvert k,\theta;\alpha\rangle_1)^*\]

因此$T^T(\rvert k,\theta;\alpha\rangle_1)^*$是$g_2(-k,\theta)$的本征态,其本征值也是$E_\alpha(k,\theta)$。将$g_2(-k,\theta)$的本征态$\rvert -k,-\theta,\beta\rangle_2$展开

\[T^T(\rvert k,\theta;\alpha\rangle_1)^*=\sum_\beta U_{\alpha\beta}(k,\theta)\rvert -k,-\theta;\beta\rangle_2\]

$g_1,g_2$系统的Berry位相规范矢量满足

\[a_{1j}^{\alpha\beta}(k,\theta)=-i\langle k,\theta;\alpha\rvert\partial_j\rvert k,\theta;\beta\rangle_1=-i[\sum_{\gamma,\delta}U^*_{\alpha\gamma}\langle -k,-\theta;\gamma\rvert\partial_j(U_{\beta\delta}\rvert -k,-\theta;\delta\rangle_2)]^*\\ =\sum_{\gamma,\delta}U_{\alpha\gamma}a_{2j}^{\gamma\delta*}(-k,-\theta)(U^\dagger)_{\delta\beta}-i\sum_\gamma U_{\alpha\gamma}(k,\theta)\partial_j U^*_{\beta\gamma}(k,\theta)\label{ha23}\]

总而言之$a_{1j}^{\alpha\beta}(k,\theta)$等于$a_{2j}^{\alpha\beta}$只是相差一个规范变换,Berry位相去曲率满足

\[f_{1ij}^{\alpha\beta}(k,\theta)=U_{\alpha\gamma}f^{\gamma\delta*}_{2ij}(-k,-\theta)(U^\dagger)_{\delta\beta}\]

这就使得$C_2[g_1(k,\theta)]=C_2[g_2(k,\theta)]$。这里就证明了对任意两个对称插值$h,h^{‘}$都有 $C_2[h(k,\theta)]-C_2[h^{‘}(k,\theta)]=2C_2[g(k,\theta)]=0\quad\text{mod}\quad 2$,则相对第二Chern数宇称为

\[N_3[h_1(k),h_2(k)]=(-1)^{C_2[h(k,\theta)]}\]

它对任意两个时间反演不变的$(3+1)$维绝缘体都是well defined,与插值选取是无关的。与$(1+1)$ 情况相似,此时可以选取一个真空哈密顿量$h_0$作为参考,所有满足$N_3[h_0,h]=-1$的称为$Z_2$非平庸,$N_3[h_0,h]=1$是平庸的。通过(\ref{ha23})的推导以及TRI哈密顿量满足$T^\dagger h(-k,-\theta)T=h^T(k,\theta)$,Berry位相规范势满足$a_i(k)=Ua_i(-k)U^\dagger-iU\partial_iU^\dagger$,从而可以得到电磁极化$P_3$满足

\[2P_3=\frac{i}{24\pi^2}\int d^3k\epsilon^{ijk}\text{Tr}[(U\partial_iU^\dagger)(U\partial_jU^\dagger)(U\partial_kU^\dagger)]\in Z\]

这里仅有两个不等价TRI $P_3$值$P_3=0,P_3=1/2$。对两个哈密顿量$h_1,h_2$其第二Chern数满足$C_2[h(k,\theta)]=2(P_3[h_2]-P_3[h_1])$ mod 2,所以$P_3$的差值决定了相对Chern宇称$N_3[h_1,h_2]=(-1)^{2(P_3[h_1]-P_3[h_2])}$。 因此平庸的哈密顿量有$P_3=0$,而非平庸的为$P_3=1/2$。

当得到了$Z_2$分类之后,由这个拓扑量子数对应的物理结果可以通过

\[S_{3D}=\frac{1}{4\pi}\int d^3xdt\epsilon^{\mu\nu\sigma\tau}P_3(x,t)\partial_\mu A)\nu\partial_\sigma A_\tau\]

来进行研究。一个粒子空穴对称$Z_2$分类的绝缘体在其边界上将会存在零能束缚态,且边界上存在半整数电荷。同样的,对于非平庸的$(3+1)$维绝缘体同样由拓扑保护的表面态。而研究$(3+1)$维表面态最简单的方法就是再次进行维度约化。对于任意三维哈密顿量$h_1(k)$一个插值$h(k,\theta)$可以放置在$h_1$和真空哈密顿量$h_0$之间,如果把$\theta$看做是第四个动量,那么$h(k,\theta)$就定义了一个$(4+1)$维的能带绝缘体,而且它还要满足时间反演不变的限制。沿$z$方向取开边界条件,其余三个方向都是周期边界,当第二Chern数$\C_2[h]$非零时,在表面上此时将会有$\rvert C_2[h]\rvert$种$(3+1)$维手性费米子。也就是说在表面态的3D布里渊区中将会有$\rvert C_2[h]\rvert$个节点$(k_{xn},k_{yn},\theta_{n}),n=1,\cdots,\rvert C_2[h]\rvert$,这里的能谱$E_n(k_x,k_y,\theta)$是无能隙的并有线性色散的Dirac锥。

从时间反演对称可以得到$(k_x,k_y,\theta),(-k_x,-k_y,-\theta)$处的能谱是完全相同的,即如果$(k_x,k_y,\theta)$是节点则$(-k_x,-k_y,-\theta)$也一定是;时间反演对称要求手性费米子一定是成对出现的,除了在时间反演不变动量点。

当第二Chern数是奇数的时候,在3D布里渊区中一定有奇数个Dirac锥在八个高对称点上。

$Z_2$非平庸绝缘体物理性质

鱼油非平庸的绝缘体有磁电极化$P_3=1/2$ mod $1$, 根据

\[S_{3D}=\frac{1}{4\pi}\int d^3xdt\epsilon^{\mu\nu\sigma\tau}P_3(x,t)\partial_\mu A_\nu\partial_\sigma A_\tau\label{ha24}\]

体态有效作用量为

\[S_{3D}=\frac{2n+1}{8\pi}\int d^3xdt\epsilon^{\mu\nu\sigma\tau}\partial_\mu A_\nu\partial_\sigma A_\tau,\quad n=P_3-1/2\in Z\label{ha25}\]

在时间反演对称下,$\epsilon^{\mu\nu\sigma\tau}\partial_\mu A_\nu\partial_\sigma A_\tau=2\mathbf{E}\cdot\mathbf{B}$是奇函数,有效作用量(\ref{ha24})破坏了时间反演对称。然而,当空间流形是闭合的时候(所有的方向都是周期边界),$\int d^3xdt\epsilon^{\mu\nu\sigma\tau}\partial_\mu A_\nu\partial_\sigma A_\tau$的结果是量子化的$8\pi^2m,m\in Z$。y因此$S_{3D}=(2n+1)m\pi$,从而作用量$e^{iS_{3D}}=e^{im\pi}=(-1)^m$是时间反演不变的,而且与$n$无关(n是$P_3$的整数部分)。

因此在一个闭合的时空流形上,拓扑作用量(\ref{ha25})与$Z_2$非平庸时间反演拓扑绝缘体的有效理论结果是一致的,极化$P_3$的整数部分并不是一个物理量。但是在开边界条件的时候,情况变的有所不同,在时空流形上有边界的时候$S_{3D}$的值不再是量子化的,基矢$P_3=1/2$ or $0$,在这种情况下$P_3$的整数部分并不会进入到$e^{iS_{3D}}$中并且物理,它的值会依赖于边界的具体细节。

为了理解开边界时候的物理,考虑在$z=0$两边分别是拓扑不等价的系统,有效作用量(\ref{ha24})可以写为

\[S_{3D}=\frac{1}{4\pi}\int d^3 xdt \epsilon^{\mu\nu\sigma\tau}A_\mu\partial_\nu P_3\partial_\sigma A_\tau\]

因为当$z<0P_3=1/2$ mod1 ,当$z>0$是$P_3=0$ mod 1,此时可以有

\[\partial_zP_3=(n+1/2)\delta(z)\]

这里的$n\in Z$依赖于表面拓扑非平庸的细节。在这种情况下有效作用量可以约化到表面上$(2+1)$维的Chern-Simons项

\[S_\text{eff}=-\frac{2n+1}{8\pi}\int dxdydt\epsilon^{3\mu\nu\rho}A_\mu\partial_\nu A_\rho\label{ha26}\]

这与前面在$P_3$的畴壁上存在量子霍尔效应的结论一致。$Z_2$非平庸绝缘体上表面上的Hall电导为$\sigma_H=(n+1/2)/2\pi$,它是一个半奇数乘以量子$e^2/h$。从上面分析中也可以得到在非平庸绝缘体表面上总是存在奇数个$(2+1)$维Dirac费米子。因此表面上的半量子Hall效应可以从无质量Dirac费米子的宇称反常简单理解。

由Dirac费米子携带的Hall电导只有在费米子质量不为零的时候才是well defined, 也就是说此时应该存在能隙。

联系哈密顿量模型$H=k_x\sigma^x+k_y\sigma^y+m\sigma^z$,其Berry曲率可以通过(\ref{c1})计算,矢量${\bf d}$为${\bf d}=(k_x,k_y,m)$其对应的Hall电导为

\[\sigma_H=\frac{1}{4\pi}\text{sgn}(m)(=\frac{e^2}{2h}\text{sgn}(m))\]

现在考虑拓扑绝缘体表面具有$(2n+1)$个无能隙的Dirac锥,从前面的讨论中可以知道,在不破坏时间反演对称的情况下,至少由一个Dirac锥是不打开能隙的,对每个Dirac锥考虑质量项$m_i,i=1,2,\cdots,2n+1$,诱导出的净Hall电导为$\sum_{i=1}^{2n+1}\text{sgn}(m_i)/4\pi$。由于$\sum_{i=1}^{2n+1}\text{sgn}(m_i)$s是奇整数,此时得到的Hall电导与Chern-Simons理论(\ref{ha26})得到的一致。从这个讨论同样可以理解有效作用量(\ref{ha26})描述了一个时间反演破缺的表面,尽管其体态仍然是时间反演不变的。

体态的拓扑要求这里由1/2个量子的Hall电导,而表面的时间反演破缺则决定了整数部分n。这个结论与粒子空穴对称$(1+1)$维系统终端会存在一个半整数的电荷是完全类似的。局域在绝缘体链一端的电荷为$(n+1/2)e$,整数部分$n$依赖于时间反演破缺的表面,而$1/2$则是由体态拓扑 所保证的。

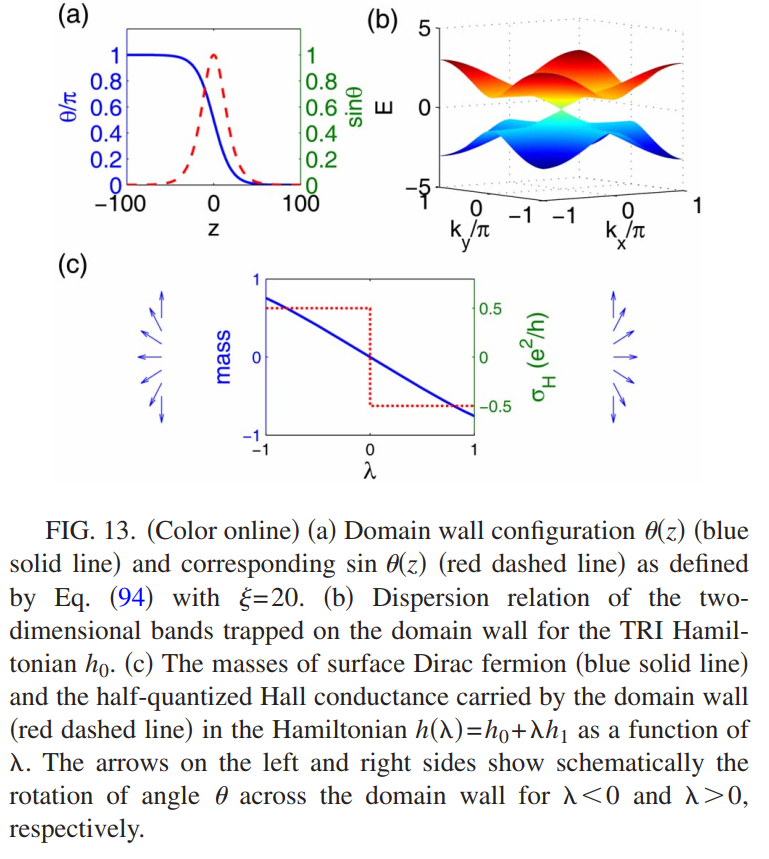
下面从更加明确的物理角度来研究这个表面态,通过一个Dirac格点模型来作为例子,考虑一个$(3+1)$维的格点模型(\ref{ha20}),并且有一个$\theta(\vec{x})$畴壁存在

\[\theta(\vec{x})=\theta(z)=\frac{\pi}{2}[1-\tanh(z/4\xi)],\quad \theta(z\rightarrow-\infty)=\pi,\theta(z\rightarrow+\infty)=0\]

其构型如下图所示

当沿着$x,y$方向为周期边界时,哈密顿量可以进行块对角化

\[\begin{equation}\begin{aligned}H&=\sum_{z,k_x,k_y}[\psi^\dagger_{k_x,k_y}(z)(\frac{c\Gamma^0-i\Gamma^3}{2})\psi_{k_x,k_y}(z+1+\text{H.c})]\\&+\sum_{z,k_x,k_y}\psi^\dagger_{k_x,k_y}(z)[(m+c\cos\theta(z)+c\cos k_x+c\cos k_y)\Gamma^0+\sin k_x\Gamma^1+\sin k_y\Gamma^2]\psi^\dagger_{k_x,k_y}(z)\\&+\sum_{z,k_x,k_y}\psi^\dagger_{k_x,k_y}(z)\sin\theta(z)\Gamma^4\psi^\dagger_{k_x,k_y}(z)\equiv H_0+H_1\end{aligned}\end{equation}\label{ha27}\]

在时间反演变化下$\Gamma^0$是偶函数$\Gamma^{1,2,3,4}$是奇函数性质,因此(\ref{ha27})中只有最后一项是时间反演奇函数项,因为$\sin\theta(z)$项的存在,它会局域点边界上。将哈密顿量分解为$H=H_0+H_1$,这里$H_1$代表的就是(\ref{ha27})中的最后一项,而$H_0$则是其余满足TRI的项。

第一$h_0,h_1$分别对应$H_0,H_1$,哈密顿量$H_0$描述$\theta=0,\theta=\pi$交接处的时间反演不变面。对于$-4c < m < -2c$参化的哈密顿量$H_0(\theta),\theta\in[0,2\pi]$有一个Chern数$C_2=1$,因此对于$\theta=0,\theta=\pi$的系统有相对Chern宇称为-1。可以进行检验对于$\theta=0,-4c < m < -2c$哈密顿量与$m\rightarrow-\infty$是绝热连接的。因此$\theta=0,\theta=\pi$对应的分别是$Z$的拓扑平庸与非平庸相。因此对于$H_0$在$z$的畴壁处,会存在奇数个无能隙的Dirac锥。通过数值的方式同样可以确定对于$h_0$在$(k_x,j_y)=(0,0)$存在一个Dirac锥。接下来研究$h_1$的作用,它满足${\Gamma^4,h_0=0}$满足反对易关系,则是一个质量项,表面Dirac锥的有效哈密顿量为$h_\text{surf}=k_x\sigma_x+k_y\sigma_y$是个合适的基矢,它与$\Gamma^4$反对易。在希尔伯特空间中与$H_\text{surf}$反对易的项只有$\sigma_z$,因此在格点模型中$\Gamma^4$的作用是诱导出质量项$m\sigma_z$。更加准确的关于$m$的幅值和符号可以通过微扰理论进行计算。$H-\text{surf}$的两个零能表面态为$\rvert k=0,\alpha\rangle,\alpha=1,2$,在有效理论中矩阵$\sigma_x,\sigma_y$的表示为

\[\sigma_{\alpha\beta}^{i}=\langle k=0,\alpha\rvert\frac{\partial h_0}{\partial k_i}\rvert_{k=0}\rvert k=0,\beta\rangle,\quad i=x,y\]

$\sigma_z$可以表示为$-i\sigma_x\sigma_y$,因此质量m由

\[m=\frac{1}{2}\sum_{\alpha\beta}\sigma_{\alpha\beta}^z\langle k=0,\beta\rvert h_1\rvert k=0,\alpha\rangle\]

决定。考虑一个参数化的哈密顿量$h=h_0+\lambda h_1$,表面Drirac费米子的质量在$\lambda\rightarrow 0$的时候正比于$\lambda$。 如上图(c)所示, 当$\lambda<0$的时候表面Hall电导为$\text{sgn}(\lambda)/4\pi。$表面Hall电导同样可以从有效理论进行计算。 对于$\lambda=1$位相场$\theta$从$\pi$变到$0$,对应的Hall电导为$\sigma_H=\int_{-\infty}^{+\infty}dP_3(z)/2=\int_0^\pi dP_3(\theta)/2\pi=-1/4\pi$。对于$\lambda=-1$可以考虑将$H(\theta)$中的$\theta(z)$替换成$-\theta(z)$,这个操作保持了$h_0$不变但是改变了$h_1$的符号,最终是的$\theta$的winding从$-\pi$变到了$0$,对应的Hall电导为$\sigma_H=\int_{-\pi}^0dP_3(\theta)/2=1/4\pi$。这两种情况对应的$\theta$的winding如上图(d)所示。

物理上,时间反演对称破缺项来源于磁场或者表面上的局域磁矩(可能来源于表面相互作用导致的自发时间反演对称破缺)。一旦这样的”时间反演破缺表面场”(M)出现,有效作用量$S_{3D}=\frac{1}{4\pi}\int d^3 xdt \epsilon^{\mu\nu\sigma\tau}A_\mu\partial_\nu P_3\partial_\sigma A_\tau$在开边界的时候是well defined, 它描述了$Z_{2}$非平庸绝缘体对电磁场的响应。 实际上,时间反演 破缺场应该被认为是施加在TRI系统上的外场,此时有效作用量$S_{3D}$描述的是一个结合M和电磁场$A_\mu$系统的非线性响应。对于一个占据空间大小为$\mathcal{V}$的$Z_2$非平庸系统,其边界为$\partial\mathcal{V}$,$P_3$的空间梯度为

\[\nabla P_3(\vec{x})=(g[M(\vec{x})]+\frac{1}{2})\int_{\partial\mathcal{V}}d\hat{\bf n}\delta^3(\vec{x}-\vec{y})\]

这里$g[M(\vec{x})]\in Z$是有时间反演破缺场$M(\vec{x})$决定的winding的整数部分,$\hat{\bf n}$是表面的法线方向。在这种$\nabla P_3$的构型下$S_{3D}$可以约化成表面Chern-Simons作用量

\[S_\text{surf}=\frac{1}{4\pi}\int_{\partial\mathcal{V}}d\hat{n}(g[M(\vec{x})]+\frac{1}{2})\epsilon^{\mu\nu\sigma\tau}A_\nu\partial_\sigma A_\tau\label{ha28}\]

因为通常$g[M(\vec{x})]$只能取离散的值,非平庸绝缘体表面将会有几个畴壁对应着不同的Hall电导。

磁化诱导量子Hall效应

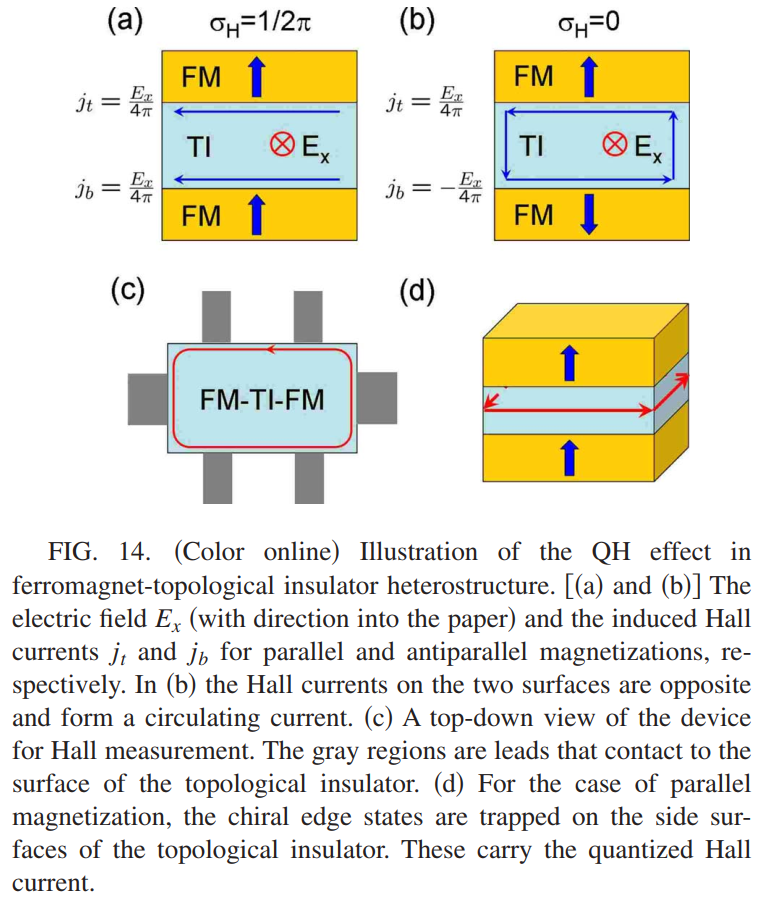
考虑如上图所示的两层题词层具有平行或者反平行的磁化方向,一个标准的六终端设置可以执行平面Hall电导的测量,净Hall电导是有上下两个表面的和贡献的。当拓扑绝缘体是均匀的时候,一个外指向的磁化矢量将会有相同的效应,无论那个表面上存在这样的磁化。假设上面有电场$\mathbf{E}=E_x\hat{\bf x}$诱导的Hall电流$\mathbf{j}_t=\hat{\bf n}_t\times \mathbf{E}/4\pi$,下表面与上表面的公式相同$\mathbf{j}_b=\hat{\bf n}_b\times \mathbf{E}/4\pi$。因为上下表面的法线方向相反$\hat{\bf n}_t=-\hat{\bf n}_b=\hat{\bf z}$,电流满足$\mathbf{j}_t=-\mathbf{j}_b$,如上图所示。最终,反平行磁化诱导出净为零的Hall电流,平行磁化诱导出的$\sigma_H=e^2/h$。和整数量子Hall效应相同,这里量子化的Hall电导是由手性边界态贡献的。由图14(a)可以看到,磁化矢量在上下表面上的方向是相反的,虽在在全局$x,y,z$基矢上磁化方向是相同的,但是通过每个面上的法线方向$\hat{\bf n}$来定义,两个表面上的Hall电导是相反的。也就是说在表面Chern-Simons有效作用量(\ref{ha28})中,对上表面而言$g[M(\vec{x})]$是$0$但是对下表面则是$-1$。结果就是在两个表面的边界交界处就会有Hall电导。这就类似于通常量子霍尔系统中在$\nu=0$和$\nu=1$的区域内,在畴壁处会补货手性费米流体,这正是实验上锁观测到的净Hall效应。

这里边界面是两维的,所以一般情况下除了一致手性的边界态之外,同样会有其他无寿星的传播模式,但是这些无手性的态并不会改变净的稳定的手性边界态,因此这里总是会存在一支向左或者向右运动的边界态。

这些边界态的稳定性是受到体态能隙保护的,在此时是有磁化诱导的能隙$E_M$。在满足下面两个要求的情况下是可以观测到这种效应的:

• 温度$k_BT « E_m$
• 当化学势在由磁化诱导上下表面能隙之间

拓扑磁电效应

拓扑磁电效应是由$P_3$诱导出来,可以通过(\ref{ha22})与$\vec{P}=-\frac{\vec{B}}{2\pi}(P_3+\text{const})$描述,接下来考虑在非平庸拓扑绝缘体中实现这种效应。和表面量子Hall效应相同,$P_3$的整数部分是由磁化决定的,考虑一个铁磁-拓扑绝缘体-铁磁的异质结,入托14(b)所示,因为具有反平行的磁化,电场$E_x$诱导的电流在上下表面上的方向是相反的。当考虑一个如上描述的没有Hall bar的孤立系统,形成了一个循环的电流,在电场的作用下会诱导出平行或者反平行的磁化。然而当考虑图14(b)所示的几何结构时,循环电流在无能隙的边界面上会有耗散,违反了拓扑磁电(TME)的绝热条件。为了得到TME需要在边界面上存在破坏时间反演的能隙,这个可以通过图15(a)中的圆柱形结构来实现。

在圆柱体的表面上存在指向面外的磁化还有固定的Hall电导$\sigma_H=(n+\frac{1}{2})e^2/h$。当平行于圆柱体施加一个电场后,在边界面上就会诱导出沿着切线方向的循环电流,其强度为$j_t=\sigma_HE$。这个循环电流的出现与在表面上束缚一个常数的磁化$M=j_t/c=(n+1/2)\frac{e^2}{hc}E$是相同的,它的方向与电场是反平行的。总之,表面的Hall电流就像是拓扑磁化电流,表面的半Hall效应就等价于体态磁化贡献的拓扑

\[\mathbf{M}_t=-(n+\frac{1}{2})\frac{e^2}{hc}\mathbf{E}\]

这里需要指出的是,响应系数等于$1/4\pi$成精细结构常数$\alpha=e^2/\hbar c$的奇数倍。通常情况下如果一个电场施加在方向方向为$\hat{\bf n}$的拓扑绝缘体表面上行,Hall电流为$\mathbf{j}_H=(n+1/2)\frac{e^2}{h}\hat{\bf n}\times\mathbf{E}$, 这与上式给出的磁化产生的磁化流是一致的。结合通常非拓扑的磁化响应$\mathbf{M}_c$,可以得到总的磁化为$\mathbf{M}=\mathbf{M}_c+\mathbf{M}_t$,则修改后的方程为

\[\mathbf{H}=\mathbf{B}-4\pi\mathbf{M}_c+(2n+1)\frac{e^2}{\hbar c}\mathbf{E}\label{ha29}\]

同样的电场和磁场的诱导也会发生在平行于圆柱体施加磁场的情况下,如图15(b)所示。当磁场从零逐渐打开时,平行于边界面的循环电流将会被产生,诱导出的Hall电流为$j\simeq dB/dt$,其方向会平行或者反平行与磁场方向。最终,在上下表面会有正比于磁场$B$的电荷密度积累,因此又磁场诱导电荷极化的拓扑贡献为

\[\mathbf{P}_t=(n+\frac{1}{2})\frac{e^2}{hc}\mathbf{B}\]

将常规与拓扑的响应结合起来可以得到

\[\mathbf{D}=\mathbf{E}+4\pi\mathbf{P}_c-(2n+1)\frac{e^2}{\hbar c}\mathbf{B}\label{ha30}\]

通常的Maxwell’s方程加上(\ref{ha29})和(\ref{ha30})就可以完整的描述3D拓扑绝缘体的电动力学。另外一个替代描述就是利用常规的关系

\[\mathbf{D}=\mathbf{E}+4\pi\mathbf{P}_{c},\quad \mathbf{H}=\mathbf{B}-4\pi\mathbf{M}_c\]

外加上一些被拓扑相修正的Maxwell’s方程,包含拓扑相$S_{3D}=\frac{1}{4\pi}\int d^3xdt\epsilon^{\mu\nu\sigma\tau}P_c(x,t)\partial_\mu A_\nu\partial_\sigma A_\tau$后的电磁场总的作用量为

\[S_\text{tot}=S_\text{Maxwell}+S_\text{topo}=\int d^3xdt[\frac{1}{16\pi}F_{\mu\nu}F^{\mu\nu}+\frac{1}{2}F_{\mu\nu}\mathcal{P}^{\mu\nu}-\frac{1}{c}j^\mu A_\mu]+\frac{\alpha}{16\pi}\int d^3xdt P_3\epsilon^{\mu\nu\sigma\tau}F_{\mu\nu}F_{\sigma\tau}\label{ha32}\]

$\alpha\equiv e^2/\hbar c$是精细结构常数,$\mathcal{P}^{0i}=P^i,\mathcal{P}^{ij}=\epsilon^{ij}M_k$分别是电,磁极化矢量。可以通过对$A_\mu$求变分得到运动方程

\[\frac{1}{4\pi}\partial_\nu F^{\mu\nu}+\partial_\nu\mathcal{P}^{\mu\nu}+\frac{\alpha}{4\pi}\epsilon^{\mu\nu\sigma\tau}\partial_\nu(P_3F_{\sigma\tau})=\frac{1}{c}j^\mu\]

这些方程可以写成更加熟悉的形式

\[\nabla\cdot\mathbf{D}=4\pi\rho+2\alpha(\nabla P_3\cdot\mathbf{B})\\ \nabla\times\mathbf{H}-\frac{1}{c}\frac{\partial\mathbf{D}}{\partial t}=\frac{4\pi}{c}\mathbf{j}-2\alpha((\nabla P_3\times \mathbf{E})+\frac{1}{c}(\partial_t P_3)\mathbf{B})\\ \nabla\times\mathbf{E}+\frac{1}{c}\frac{\partial\mathbf{B}}{\partial t}=0\\ \nabla\cdot\mathbf{B}=0\label{ha31}\]

这里$\mathbf{D}=\mathbf{E}+4\pi\mathbf{P}_c,\mathbf{H}=\mathbf{B}-4\pi\mathbf{M}_c$仅仅包含了非拓扑的贡献。 这些是轴子电动力学的运动方程。通过将拓扑项移动到左边,并根据(\ref{ha20})和(\ref{ha30}重新改写$\mathbf{D,H}$,取$P_3=n+1/2$就可以得到传统的Maxwell’s方程。

因为在拓扑绝缘体中体态存在时间反演对称,不可能由其他非拓扑的机制来对磁电系数由贡献,这也保证了拓扑磁电效应的鲁棒性。

这里要强调一下,在拓扑绝缘体中$P_3$的值只有在当打开能隙的表面上存在磁化的时候才能被确定,如图15(c),选择一个路径$L$从参考点深入到真空中,$P_3$可以被计算$P_3(\vec{x})=\int_{\vec{x}_0L}^{\vec{x}}dl\cdot \nabla P_3$。然而这个结果仅仅适用于当结果不依赖于路径的时候。如果一个磁化的壳包裹在拓扑绝缘体表面上,在界面的任何处磁化方向都指向外侧,当$P_3$穿过界面的时候在不同位置处的改变量都是相同的,此时体态的$P_3$是well defined,在这种情况下,方程(\ref{ha29},\ref{ha30})也都是well defined,如果磁化的方向反向,那么$P_3$的整数部分会发生改变。另一方面,当在表面上存在磁化方向的畴壁时,在体态中此时整数部分的$P_3$不是well defined,(\ref{ha29},\ref{ha30})并不能使用,如图15(d)所示。方程(\ref{ha29},\ref{ha30}})失败是因为此时边界上存在量子霍尔边界流,此时需要更加一般形式的Maxwell’s方程(\ref{ha31})来包含这些边界电流的贡献。这些分析同样提供了表面Hall效应新的图像,即表面上的量子霍尔效应是由寄居在$P_3$场vortex ring上的手性边界态产生的。只有当这种边界态不存在,表面是full gapped,电磁响应才可以用(\ref{ha29},\ref{ha30})来描述。

低频Faraday旋转

通过一个电容施加电场,并利用超导量子干涉仪来探测磁场从而可以观测TME效应,同样的也可以利用Faraday或者Kerr旋转来进行探测。修改后的Maxwell方程(\ref{ha31})可以运用到地外一个现象中-光子传播系统。这里需要注意方程(\ref{ha32})只能应用到力能极限$E « E_g$,这里$E_g$是表面态的能隙。用来探测系统拓扑性质的光子频率应该是低频光子$\omega « E_g/hbar$。

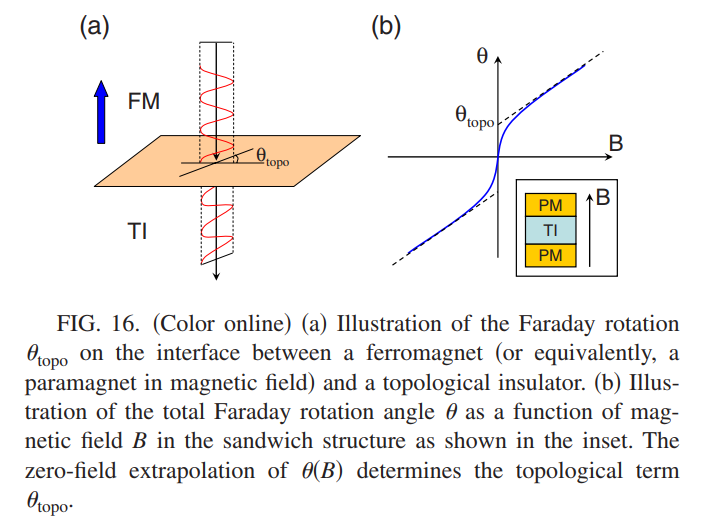
在$z=0$处考虑一个铁磁-拓扑绝缘体的界面,如上图所示,正常的线性偏振光可以表示为

\[\mathbf{A}(z,t)=\left\{\begin{array}{c}\mathbf{a}e^{i(-kz-\omega t)}+\mathbf{b}e^{i(kz-\omega t)},\quad z>0\\ \mathbf{c}e^{i(-k^{'}z-\omega t)},\quad z<0\end{array}\right.\]

这里的$k=\omega/v,k^{‘}=\omega/v^{‘}$分别是$z>0,z<0$区域的波矢。 方程(\ref{ha32})中的$\nabla P_3$项在$z=0$处会贡献一个非常规的边界条件。定义$\nabla P_3=\Delta\hat{\bf z}\delta(z)$(满足$\Delta -1/2\in Z$),边界条件为

\[{\bf a+b=c},\quad \hat{\bf z}\times [k(-\mathbf{a}+\mathbf{b})/\mu+k^{'}\mathbf{c}/\mu^{'}]=-\frac{2\alpha\Delta\omega}{c}\mathbf{c}\]

这里$\epsilon,epsilon^{‘}$和$\mu,\mu^{‘}$分别是$z>0,z<0$处的的介电常数和透射率。简记$a_\pm=a_x\pm ia_y,b_\pm,c_\pm$也一样,上面的方程可以得到

\[a_+=\frac{1}{2}[1+\frac{k^{'}/\mu^{'}-2i\alpha\Delta\omega/c}{k/\mu}]c_+\]

当入社波矢$\mathbf{a}$是线极化的,那么传播波矢$\mathbf{c}$同样是线极化的,极化平面的旋转角度为

\[\theta_\text{topo}=\arctan\frac{2\alpha\Delta}{\sqrt{\epsilon/\mu}+\sqrt{\epsilon^{'}/\mu^{'}}}\label{ha33}\]

这里总是假设铁磁材料的磁化方向是垂直于$xy$面的,因此$\mathbf{H}=\mu\mathbf{B}$总是一个面内的磁场。

由于铁磁材料同时也会诱导Fraday旋转,在测量拓扑贡献(\ref{ha33})的时序必须对其进行区分,将铁磁层替换成具有更大磁化率的顺磁材料并施加磁场进行极化,此时磁化正比于磁场,因此体态贡献的Faraday旋转正比于磁场。净Faraday旋转为$\theta=\theta_\text{topo}^{(t)}+\theta_\text{topo}^{(b)}+\theta_\text{bulk}$,它与磁场的依赖关系为

\[\theta(B)=\mu B+2\text{sgn}(B)\arctan\frac{2}{\sqrt{\epsilon/\mu}+\sqrt{\epsilon^{'}/\mu^{'}}}\]

最终,拓扑贡献可以通过改变磁场的方向来得到,也可以通过外推$\theta(B)$在$B\rightarrow 0^+$的极限下。在实验上探测这个效应的主要困难在于低频要求$\omega « E_g/\hbar$, 对于通常的带隙$E_g=10 meV$,此时对应的频率为$f=\omega/2\pi « 2.4 THz$,这对应着微波的远红外区域。原则山对于带隙较大的拓扑绝缘体可以实现较为精确的测量Faraday旋转。同样可以通过通过测量反射波的旋转角(Kerr效应)。

维度约化至$(2+1)$维

将维度约化过程再进行一次就可以得到$(2+1)$维TRI绝缘体的有效理论, 对他可以定义一个$Z_2$的拓扑分类,与$(0+1)$维粒子空穴对称的$Z_2$分类是完全类似的. 这个$(2+1)$维的$Z_2$非平庸的项对应的正是量子自旋霍尔绝缘体.

$$(2+1)$维绝缘体有效理论

在前面已经研究了如何将一个$(3+1)$维绝缘体通过一个参数场$\theta(\vec{x},t)$通过维度约化与$(4+1)$维绝缘体联系起来, 同样的也可以从$(4+1)$维通过维度约化来定义$(2+1)$维绝缘体,下面就通过格点模型来研究如何实现维度约化并推导有效理论.

从格点Dirac模型

\[H[A]=\sum_{n,i}[\psi^\dagger_n(\frac{c\Gamma^0-i\Gamma^i}{2})e^{iA_{n,n+\hat{i}}}\psi_{n+\hat{i}}+\text{H.c}]+m\sum_n\psi^\dagger_n\Gamma^0\psi_n\]

出发并选择一个特殊的规范$A_{n+\hat{w},n+\hat{w}+\hat{i}}=A_{n+\hat{z},n+\hat{z}+\hat{i}}$得到哈密顿量

\[\begin{equation}\begin{aligned}H[A]&=\sum_{k_z,k_w,\mathbf{x}}\sum_{s=1,2}[\psi^\dagger_{\mathbf{x};k_z,k_w}(\frac{c\Gamma^0-i\Gamma^s}{2})e^{iA_{\mathbf{x},\mathbf{x}+\hat{s}}}\psi_{\mathbf{x}+\hat{s};k_z,k_w}+\text{H.c}]\\ &+\sum_{k_z.k_w.\mathbf{x}}\sum_{s=1,2}\psi^\dagger_{\mathbf{x};k_z,k_w}\cdot\{ \sin(k_z+A_{\mathbf{x}3})\Gamma^3+\sin(k_w+A_{\mathbf{x}4})\Gamma^4\\ &+ [m+c\cos(k_z+A_{\mathbf{x}3})+c\cos(k_w+A_{\mathbf{x}4})\Gamma^0]\psi^\dagger_{\mathbf{x};k_z,k_w} \},\quad \mathbf{x}=(x,y)\end{aligned}\end{equation}\]

与$(3+1)$维情况相同,在$z,w$方向的规范场可以通过参数场来代替$(k_z+A_{\mathbf{x}3})\rightarrow \theta_\mathbf{x},(k_w+A_{\mathbf{x}4})\rightarrow \varphi_\mathbf{x}$, 则参数化之后的$(2+1)$维哈密顿量为

\[\begin{align} H_{2D}[A,\theta,\varphi]&=\sum_{\mathbf{x},s}[\psi^\dagger_\mathbf{x}(\frac{c\Gamma^0-i\Gamma^s}{2})e^{iA_{\vec{x},\vec{x}+\hat{x}}}\psi_{\mathbf{x}+\hat{s}}+\text{H.c}]\\ &+\sum_{\mathbf{x},s}\psi^\dagger_\mathbf{x}[\sin\theta_\mathbf{x}\Gamma^3+\sin\varphi_\mathbf{x}\Gamma^4+(m+c\cos\theta_\mathbf{x}+c\cos\varphi_\mathbf{x})\Gamma^0]\psi_\mathbf{x}\label{ha38} \end{align}\]

通过将费米子场积分而后将得到的有效作用量在$A_s=0,\theta=\theta_0,\varphi=\varphi_0$处进行展开,相同的非线性项与图7费曼图相同对应的拓扑项为

\[S_{2D}=\frac{G_2(\theta_0,\varphi_0)}{2\pi}\int d^2xdt\epsilon^{\mu\nu\rho}A_\mu\partial_\nu\delta\theta\partial_\rho\delta\varphi\label{ha35}\]

这里的系数$G_2(\theta_0,\varphi_0)$由关联函数(\ref{ha10})决定但不包括对$k_z,k_w$的积分

\[G_2(\theta_0,\varphi_0)=\frac{2\pi}{3}\int\frac{d^2kd\omega}{(2\pi)^3}\text{Tr}\epsilon^{\mu\nu\rho}[(G\frac{\partial G^{-1}}{\partial q^\mu})(G\frac{\partial G^{-1}}{\partial q^\nu})(G\frac{\partial G^{-1}}{\partial q^\rho})(G\frac{\partial G^{-1}}{\partial q_{\theta_0}})(G\frac{\partial G^{-1}}{\partial q_{\varphi_0}})]\\ =\frac{1}{4\pi}\int d^2k\epsilon^{ij}\text{Tr}[2f_{i\theta}f_{i\varphi}-f_{ij}f_{\theta\varphi}],\quad\mu,\nu,\rho=0,1,2,\quad i,j=1,2,\quad q^\mu=(\omega,k_x,k_y)\label{ha39}\]

此时Berry曲率是定义在$(k_x,k_y,\theta,\varphi)$的四维空间中,系数$G_2(\theta_0\varphi_0)$满足求和规则

\[\int G_2(\theta_0\varphi_0)d\theta_0d\varphi_0=2\pi C_2\]

为了进一步简化,再次引入Chern-Simons形式的$\mathcal{K}^A$

\[\mathcal{K}^A=\frac{1}{16\pi^2}\epsilon^{ABCD}\text{Tr}[(f_{BC}-\frac{1}{3}[a_B,a_C])\cdot a_D]\]

这里的$A$是对$k_x,k_y,\theta,\varphi$的求和,根据这个表达式,可以将$G_2(\theta_0\varphi_0)$表示为

\[G_2(\theta_0\varphi_0)=-2\pi\int d^2k(\partial_x\mathcal{K}^x+\partial_y\mathcal{K}^y+\partial_\theta\mathcal{K} ^\theta+\partial_\varphi\mathcal{K}^\varphi)\]

与$(3+1)$维的情况相似,只要$\mathcal{K}^{(x,y)}$是单只的,那么对动量的导数$\partial_{(x,y)}\mathcal{K}^{(x,y)}$的贡献就是零,此时可以将$G_2$表示为

\[G_2(\theta_0,\varphi_0)=\partial_\theta\Omega_\varphi-\partial_\varphi\Omega_\theta,\quad\Omega_\varphi=-2\pi\int d^2k\mathcal{K}^\theta,\quad\Omega_\theta=2\pi\int d^2k\mathcal{K}^\varphi\label{ha43}\]

这里有

\[-\mathcal{K}^\theta=-\frac{1}{16\pi^2}\epsilon^{ij}\text{Tr}[(f_{ij}-\frac{1}{3}[a_i,a_j])\cdot a_\varphi-2(f_{i\varphi}-\frac{1}{3}[a_i,a_\varphi])\cdot a_j]\]

这里对$\mathcal{K}^\varphi$也有相似的结果.

我们知道矢量$\Omega=(\Omega_\theta,\Omega_\varphi)$在参数空间$(\theta,\varphi)$和波函数规范变换下进行坐标变换的时,有确定的规范变换势的变换性质,因此当$\theta=\theta(x^\mu),\varphi=\varphi(x^\mu)$具有平滑的时空依赖定制的时候,有效的规范势$\Omega_\mu$可以定义在$(2+1)$维的时空中(我不明白这是什么意思)

\[\Omega_\mu\equiv\Omega\partial_\mu\delta\theta+\Omega_\varphi\partial_\mu\delta\varphi\label{ha34}\]

与$G_2$关联的规范曲率为

\[\partial_\mu\Omega_\nu-\partial_\nu\Omega_\mu=(\partial_\theta\Omega_\varphi-\partial_\varphi\Omega_\theta)(\partial_\mu\delta\theta\partial_\nu\delta\varphi-\partial_\nu\delta\theta\partial_\mu\delta\varphi)=G_2(\partial_\mu\delta\theta partial_\nu\delta\varphi-\partial_\nu\delta_\theta\partial_\mu\delta\varphi)\]

数学上$G_2$是在2D参数空间中第二Chern数的密度,$(\theta,\varphi)=[\theta(x^\mu),\varphi(x^\mu)]$定义乐意个从$(2+1)$维时空流形到2D参数空间的平滑映射.规范场的曲率$\Omega_\mu$则是$(2+1)$维时空中的pullback.利用(\ref{ha34})可以将有效作用量(\ref{ha35})重写为参数独立的形式

\[S_{2D}=\frac{1}{2\pi}\int d^2xdt\epsilon^{\mu\nu\tau}A_\mu\partial_\nu\Omega_\tau\label{ha36}\]

有效理论(\ref{ha36})的物理结果可以通过响应方程研究

\[j^\mu=\frac{1}{2\pi}\epsilon^{\mu\nu\rho}\partial_\nu\Omega_\rho\label{ha37}\]

方程(\ref{ha37})是量子自旋Hall效应的相应方程,其形式与量子Hall效应的响应方程相似,只不过是将外场替换成了有效的Berry位相规范场.对于Dirac模型(\ref{ha38})响应方程(\ref{ha37})可以有一个更加简明的形式.根据(\ref{ha14})动量空间中$(4+1)$维Dirac模型$h({\bf k})=\sum_ad_a({\bf k})\Gamma^a$的第二Chern数等于$\hat{\bf d(k)}$在球$S^4$上的winding.同样的对于$(2+1)$维有常数$\theta,\varphi$的Dirac模型(\ref{ha38})有形式$h({\bf k},\theta,\varphi)=\sum_ad_a({\bf k},\theta,\varphi)\Gamma^a$,则关联函数(\ref{ha39})$G_2$表示为

\[G_2(\theta,\varphi)=\frac{3}{4\pi}\int d^2k\epsilon^{abcde}\frac{d_a\partial_{k_x}d_b\partial_{k_y}d_c\partial_{\theta}d_d\partial_{\varphi}d_e}{\rvert\mathbf{d}(\mathbf{k},\theta,\varphi) \rvert^5}\]

有效规范矢势$\Omega_\mu$的曲率表示为

\[\partial_\mu\Omega_\nu-\partial_\nu\Omega_\mu=3\epsilon^{abcde}\int \frac{d^2k}{4\pi}\frac{d_a\partial_{k_x}d_b\partial_{k_y}d_c\partial_{\mu}d_d\partial_{\nu}d_e}{\rvert\mathbf{d}(\mathbf{k},\theta,\varphi) \rvert^5}\label{ha40}\]

现在考虑一个稍微不同的格点Dirac模型

\[h({\bf k,n})=\sin k_x\Gamma^1+\sin k_y\Gamma^2+(\cos k_x+\cos k_y-2)\Gamma^0+m\sum_{a=0,3,4}\hat{n}_a\Gamma^a\]

$m>0,\hat{\bf n}=(\hat{n}_0,\hat{n}_3,\hat{n}_4)$是三维单位矢量,对于这样的一个模型$\bf{d}$矢量分解为

\[{\bf d}(\mathbf{k},\theta,\varphi)=\mathbf{d}_0(\mathbf{k})+\left(\begin{array}{c}0\\ 0\\ m\hat{\bf n}\end{array}\right),\quad \mathbf{d}_0(\mathbf{k})=(\sin k_x,\sin k_y,0,0,\cos k_x+\cos k_y-2)\]

在$m « 2$的极限下,哈密顿量的连续形式为$h(\mathbf{k},\hat{\bf n})\simeq\sum_{a=1,2}k_a\Gamma^a+\sum_{b=0,3,4}m\hat{n}_b\Gamma^b$,这是由三种可能质量项的$4\times 4$Dirac模型.在这个极限下并对$\mathbf{k}$进行积分(\ref{ha40})可以得到

\[\partial_\mu\Omega_\nu-\partial_\nu\Omega_\mu=\frac{1}{2}\hat{\bf n}\cdot\partial_\mu\hat{\bf n}\times\partial_\nu\hat{\bf n}\]

这正是单位矢量$\hat{\bf n}$的Skyrmion密度,结合(\ref{ha37})就可以得到连续极限下Dirac模型的响应函数

\[j^\mu=\frac{1}{8\pi}\epsilon^{\mu\nu\tau}\hat{\bf n}\cdot\partial_\mu\hat{\bf n}\times\partial_\nu\hat{\bf n}\label{2}\]

方程(\ref{2})描述了拓扑响应,这里电荷密度和电流对分别对应着Skyrmion的密度和流.为了进一步理解方程(\ref{ha37})的物理,考虑(\ref{ha38})这个格点Dirac模型有一个绝热的时间演化$\varphi(t)=2\pi t/T$和空间畴壁构型$\theta(\vec{x})$

\[\theta(y)=\frac{\pi}{2}[1+\tanh(\frac{y}{\xi})]\]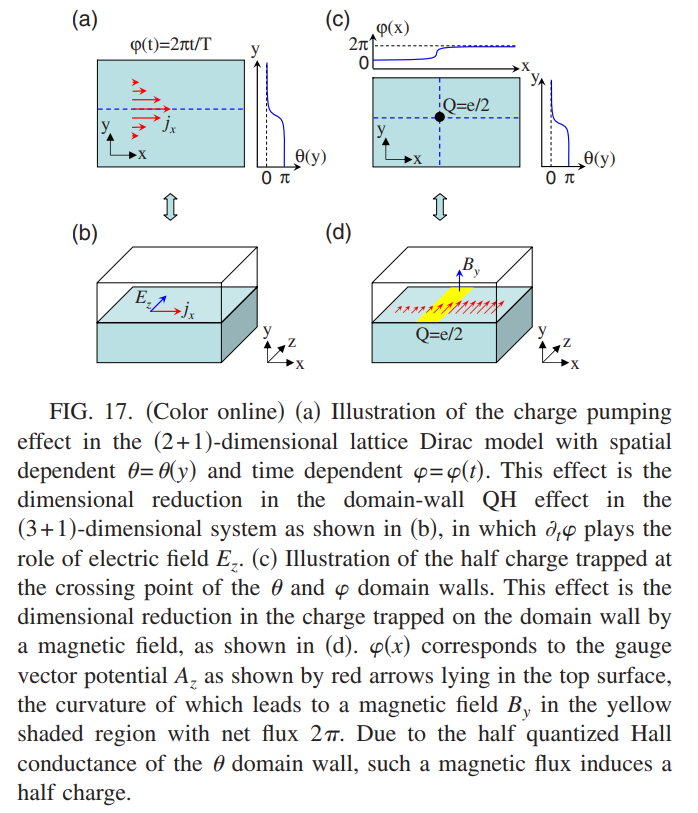

如图17(a)所示,根据(\ref{ha37})沿着畴壁的电荷流为

\[j_x=\frac{1}{2\pi}(\partial_y\Omega_t-\partial_t\Omega_y)\]

当参数$\varphi$绝热的从$0\rightarrow 2\pi$,沿着$x=0$这条线的净电荷流为

\[\int dt I_x=\int dtdy(\partial_y\Omega_t-\partial_t\Omega_y)/2\pi=\int_0^\pi d\theta\int_0^{2\pi}d\varphi(\partial_y\Omega_t-\partial_t\Omega_y)/2\pi\]

这正是对第二Chern数$\text{Tr}[\epsilon^{ABCD}f_{AB}f_{CD}]/32\pi^2$在参数空间$\theta\in[0,\pi],\varphi\in[0,2\pi]$进行的积分,这里$A,B,C,D=k_x,k_y,\theta,\varphi$.根据在$(3+1)$维情况下的讨论,可知道电磁极化$P_3$可以定义为

\[P_3(\theta)=\int d^2kd\varphi\mathcal{K}^\theta=-\int d\varphi\Omega_\varphi/2\pi\]

这意味着$\int dt I_x=-\int_0^\pi d\theta\partial_\theta P_3(\theta)$,对于$-4c < m < -2c$有$\int_0^\pi dP_3(\theta)=1/2$,对应的电荷泵浦为$\Delta Q=\int dtI_x=1/2$.总之,拓扑响应方程(\ref{ha37})的物理结果是在参数$\varphi$绝热演化的时候会诱导电子泵浦效应,在一个周期内泵浦的电子数目是正比于定义在参数空间$(k_x,k_y,\varphi)$的电磁极化$P_3$的空间梯度,特别的是在每个$\Delta\theta=\pi$的畴壁上随着$\varphi=0\rightarrow2 \pi$都会有$e/2$个电子被泵浦.

这样的一个电子泵浦效应可以看做是在$\theta$畴壁的$(3+1)$维格点Dirac模型中维度约化的班量子Hall效应.这个维度约化过程与通常的$(2+1)$为量子Hall效应到$(1+1)$为量子化泵浦效应是完全相同的.根据(\ref{ha37})在$(2+1)$维是分数的电荷效应也同样在前面被提出.为了展示这个效应,可以考虑一个和前面相同的$\theta$畴壁,并且沿$y$方向有一个$\varphi$的$2\pi$畴壁存在$\varphi(\mathbf{x})=\pi[1+\tanh(x/\xi)]$,如图17(b)所示.电荷密度为$\rho=(\partial_x\Omega_y-\partial_y\Omega_x)/2\pi$.通过对$x$方向的积分可以得到$\int\Omega_xdx=\int\Omega_\varphi d\varphi=-2\pi P_3(\theta),\rho_{1D}=\int dx\rho=\partial_y P_3(\theta),\int dy\rho_{1D}=1/2$.因此在$\theta$和$\varphi$的畴壁上会存在半整数电荷.分数电荷的存在同样可以从$(3+1)$维系统的维度约化得到.空间依赖的$\varphi(x)$对应着空间依赖的$k_z-A_z(x)$,描述在$(3+1)$维系统中垂直于2D畴壁的磁场,当$\varphi(x)$有一个$2\pi$的畴壁的时候,对应的净磁通为$2\pi$,这就会诱导出半整数电荷,如图17(b)所示.

$Z_2$分类的TRI绝缘体

首先对两个TRI $(2+1)$维绝缘体$h_1({\bf k}),h_2({\bf k})$定义一个绝热插值$h({\bf k},\theta)$满足

\[h(\mathbf{k},0)=h_1,\quad h(\mathbf{k},\pi)=h_2,\\ T^\dagger h(-\mathbf{k},-\theta)T=h^T(\mathbf{k},\theta)\]

由于$h(\mathbf{k},\theta)$对应的是一个$(3+1)$维的哈密顿量,一个$Z_2$拓扑不变量$N_3[h(\mathbf{k},\theta)]=\pm 1$可以被定义.对$(2+1)$维哈密顿量$h_1,h_2$定义$Z_2$不变量的关键点是研究$N_3[h(\mathbf{k},\theta)]$与$h(\mathbf{k},\theta)$的选择无关.考虑两个不同的参数化$h(\mathbf{k},\theta),h^{‘}(\mathbf{k},\theta)$,可以在两者之间插入一个$g(\mathbf{k},\theta,\varphi)$满足

\[g(\mathbf{k},\theta,0)=h(\mathbf{k},\theta),\quad g(\mathbf{k},\theta,\pi)=h^{'}(\mathbf{k},\theta)\\ g(\mathbf{k},0,\varphi)=h_1{\mathbf{k}},\quad g(\mathbf{k},\pi,\varphi)=h_2(\mathbf{k})\\ g^T(\mathbf{k},\theta,\varphi)=T^\dagger g(-\mathbf{k},-\theta,-\varphi)T\]

这里$g(\mathbf{k},\theta,\varphi)$对应一个$(4+1)$维绝缘体哈密顿量,其第二Chern数$C_2[g]$是被定义的.通过这个定义,$h(\mathbf{k},\theta),h^{‘}(\mathbf{k},\theta)$的第二Chern数宇称$N_3$满足$N_3[h]N_3[h^{‘}]=-1^{C_2[g]}$.同时$g(\mathbf{k},\theta,\varphi)$可以考虑为$\theta=0,\theta=\pi$系统之间的一个插值$g(\mathbf{k},0,\varphi)\equiv h_1(\mathbf{k}),g(\mathbf{k},\pi,\varphi)\equiv h_2(\mathbf{k})).

由于$h_{1,2}({\bf k})$都是独立于$\varphi$的,所以$g(\mathbf{k},0,\varphi),g(\mathbf{k},\pi,\varphi)$的Berry位相规范场的$\varphi$分量是零,结果是$-1^{C_2[g]}=N_3[g(\mathbf{k},0,\varphi)]=N_3[g(\mathbf{k},\pi,\varphi)]=1$. 因此对于任意两个插值$h,h^{‘}$都有$N_3[h]N_3[h^{‘}]=1$,因此发现$Z_2$量$N_2[h_1(\mathbf{k},h_2(\mathbf{k})]\equiv N_3[h(\mathbf{k},\theta)]$仅仅依赖于$(2+1)$维哈密顿量$h_1,h_2$. 通过定义常数哈密顿量$h_0(\mathbf{k})=h_0$作为参考,所有的$(2+1)$维哈密顿量可以通过$N_2[h_0,h(\mathbf{k})]$的值来区分,一个绝缘体满足$N_2[h_0,h]=-1$不能在不破坏时间反演对称的情况下绝热演化成平庸绝缘体$h_0$.

$Z_2$非平庸绝缘体的物理性质

与$(3+1)$维的情况相似,$Z_2$非平庸的拓扑绝缘体对应的非平庸的边界态动力学性质可以被有效理论(\ref{ha36})或者等价的利用(\ref{ha37})来描述.$Z_2$非平庸绝缘体的边界等价于平庸绝缘体与非平庸绝缘体的畴壁,接下里主要考虑这个畴壁上的性质.

正如上一节讨论的,在$h_0,h_1$中间定义一个插值$h(\mathbf{k},\theta)$满足$h(\mathbf{k},0)=h_0,h(\mathbf{k},\pi)=h_1(\mathbf{k}),T^\dagger h(-\mathbf{k},-\theta)T=h^T(\mathbf{k},\theta)$.因为$h_1$是非平庸的,对于一般的$\theta$插值$h(\mathbf{k},\theta)$想要绝热的联系$h_1,h_0$必须破坏时间反演对称,利用$h(\mathbf{k},\theta)$可以定义$h_1$到$h_0$之间的界面,考虑一个空间依赖的$\theta$

\[\theta(x,y)=\frac{\pi}{2}[1-\tanh(\frac{y}{\xi})]\]

空间依赖的哈密顿量$h(\mathbf{k},\theta(y))$和$h(\mathbf{k},-\theta)(y)$都描述了在$h_1(\text{for }y « -\xi)$和$h_0\text{for }y » \xi$之间的空间畴壁.唯一不同的是在界面处这两个哈密顿量是时间反演破缺的.现在考虑一个稍微复杂点的界面

\[h(\mathbf{k,x})=\left\{\begin{array}{c}h(\mathbf{k},\theta(y)),\quad x<0 \\ h(\mathbf{k},-\theta(y)),\quad x>0 > \end{array} \right.\]

如图18(a)所示

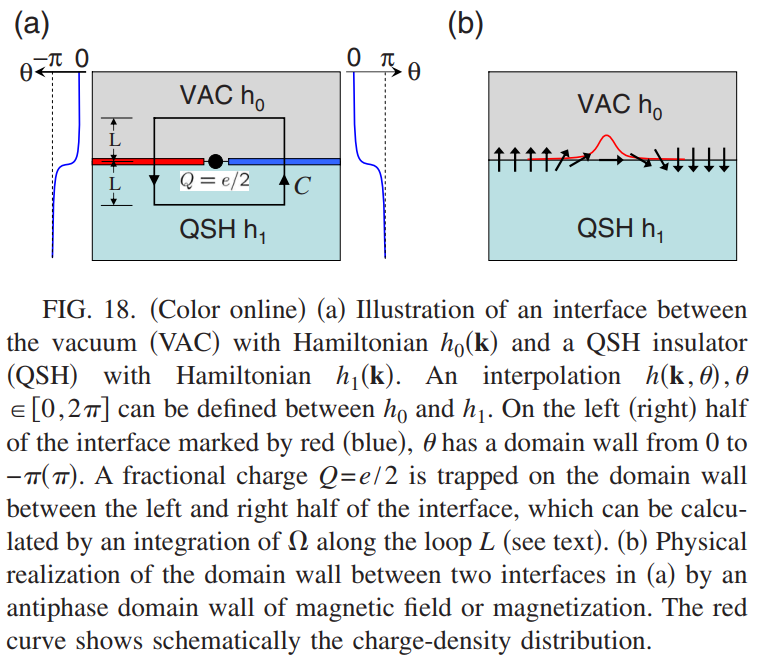
在这个系统中,时间反演对称在边界上对$x>0,x<0$是以相反的方式破缺的,$h^T[\mathbf{k},(x,y)]=T^\dagger h[-\mathbf{k},(-x,y)]T$.现在来研究局域在$x=0,y=0$上的电荷.如图18(a)所示考虑一个圈包含这个点,在由C包含的区域A中的电荷可以由(\ref{ha37})给出

\[Q=\frac{1}{2\pi}\int_Ad^2x(\partial_x\Omega_y-\partial_y\Omega_x)=\frac{1}{2\pi}\int_C\Omega\cdot d\mathbf{l}\]

当圈的尺寸相比于边界宽度$\xi$足够大的时候,这个回路的积分等价于$\theta=0\rightarrow 2\pi$的积分,对应的电荷为$Q=\int\Omega_\theta d\theta/2\pi=P_3[h(\mathbf{k},\theta)]$.根据上一节$Z_2$非平庸绝缘体的定义,对于任何在$h_0,h_1$之间的插值函数$h(\mathbf{k},\theta)$都有$P_3[h(\mathbf{k},\theta)]=1/2$ mod 1. 最终在畴壁上束缚的电荷量为$(n+1/2)e$,这个$n$是个整数,依赖于边界的具体细节.

为了更好的理解这个畴壁,在表面上考虑一个磁场来皮怀时间反演对称,当磁场变化存在一个反位相的畴壁的时候,在上面就会束缚半整数电荷,如图18(b)所示.通过对(\ref{ha37})的积分同样可以得到沿着$y$方向的1D电荷密度和电流密度

\[\rho_{1d}(x)=\frac{1}{2\pi}\int_{-L}^Ldy(\partial_x\Omega_y-\partial_y\Omega_x)\\ j_{1d}(x)=\frac{1}{2\pi}\int_{-L}^Ldy(\partial_y\Omega_t-\partial_t\Omega_y)\]

$L$是沿$y$方向的截断,满足$L » \xi$才能忽略$\rvert y\rvert > L$区域外对$\rho_{1d},j_{1d}$的贡献.根据(\ref{ha43},\ref{ha34}

)对有效规范矢势$\Omega_\mu$的定义,在深入体态或者真空态的时候$\rvert y\rvert\rightarrow +\infty$其贡献$\Omega_\mu(x,y,t)\rightarrow 0$.可以将1D密度和电流简化为

\[\rho_{1D}(x,t)=\partial_xP_3(x,t),\quad j_{1D}(x,t)=-\partial_tP_3(x,t)\]

这里$P_3(x,t)=\int_{-L}^Ldy\Omega_y(x,y,t)/2\pi$是定义在$(k_x,k_y,y)$空间中的磁电极化.当界面左右两侧的畴壁通过时间反演对称联系的时候,$2\pi P_3$的该变量在穿过畴壁的时候一定是$(2n+1)\pi$,者给出了在畴壁上的半整数电荷.

可以通过维度约化从$(3+1)$维非平庸绝缘体得到$(2+1)$维$Z_2$非平庸绝缘体的边界理论.在$h_1,h_0$之间插入$h(\mathbf{k},\theta)$,可以看成是一个$(3+1)$维TRI绝缘体,此时$\theta$代替了$k_z$.考虑$(3+1)$维的$(2+1)$维边界上一个特殊的点$y=0$,根据前面的讨论,在$(3+1)$维系统的边界上会有奇数个$(2+1)$维的Dirac费米传播.因为时间反演对称性的存在,在四个时间反演对称点一定有奇数个Dirac锥存在.对于切片$y=0$,表面态的博士为$(k_x,\theta)$.当把$\theta$考虑成参数之后,对于给定的$\theta$,表面能谱$E(k_x,\theta)$描述$(2+1)$维绝缘体的$(1+1)$边界态的色散.当$\theta=0$对应的是真空态哈密顿量$h_0$,它不会存在非平庸的边界态.因此Dirac锥只能出现在时间反演不变动量点$(k_x,\theta)=(0,\pi),(\pi,\pi)$处.为了在$(k_x,\theta)$布里渊区中又最少奇数个的Dirac锥,这里仅有一个Dirac锥可以出现在$(0,\pi)$或者$(\pi,\pi)$处,而不会在两个位置同时出现.如图19所示

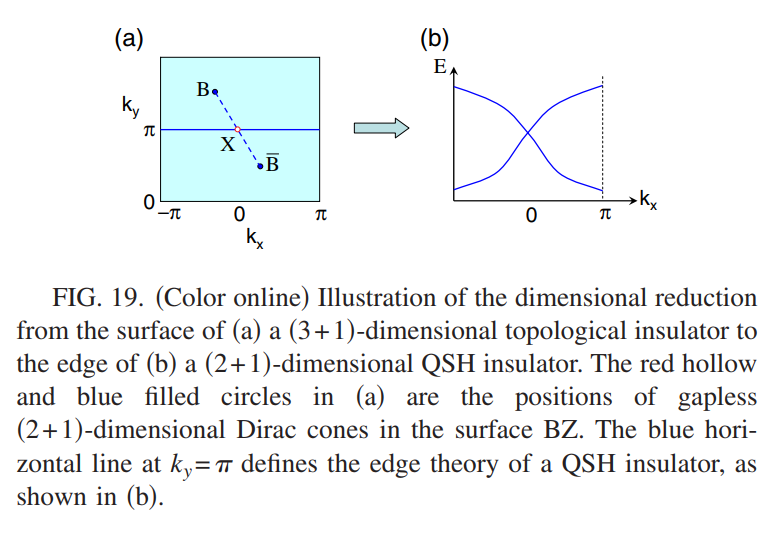
总而言之,$(2+1)$为非平庸绝缘体的有效边界理论是一个无能隙的Dirac理论

\[H=\int \frac{dk}{2\pi}v\sum_{\sigma=\pm}\sigma k\psi^\dagger_{k\sigma}\psi_{k\sigma}\]

这里$\sigma=\pm$分别表示左行与右行的边界态,这个理论与前面描述量子自旋Hall效应的结果一致,并且表明了$Z_2$非平庸绝缘体与量子自旋Hall绝缘体的等价性.一档边界态理论得到了,就可以简单的理解上面提到的分数电荷.因为存在Kramers简并,任何满足TRI的微扰并不能在边界上打开能隙,只有磁场或者其他破坏时间反演对称的项可以在边界上产生质量项$m_x\sigma_x+m_y\sigma_y$.时间反演对称同样保证了相反的磁场会诱导出相反的质量项,这意味着磁场产生一个位相相反的畴壁处,Dirac质量项会发生符号的改变,因此边界态理论是由著名的Jackiw-Rebbi模或者等价的SSH模型来描述的.

在边界上加入含时的时间反演破缺场可以实现分数电荷,并会存在量子化电荷泵浦效应.一个由含时哈密顿量$h(\mathbf{k,x},t)$描述的系统满足$h(\mathbf{k,x},0)=h[\mathbf{k},\theta(y)],h(\mathbf{k,x},t=T)=h[\mathbf{k},-\theta(y)]$,这里$\theta(y)$的构型为$\theta(x,y)=\frac{\pi}{2}[1-\tanh(\frac{y}{\xi})]$,在$t\in[0,T]$的过程中通过表面泵浦的电荷为

\[Q_\text{pump}=\int_0^Tdtj_{1D}=-[P_3(T)-P_3(0)]=-(n+\frac{1}{2})\]

在外加磁场的粒子中,当磁场绝热的从${\bf B}$转动到${\bf -B}$的过程中,上面的泵浦过程意味着将会有半个电荷被泵浦,如图20所示.

拓扑绝缘体的统一理论

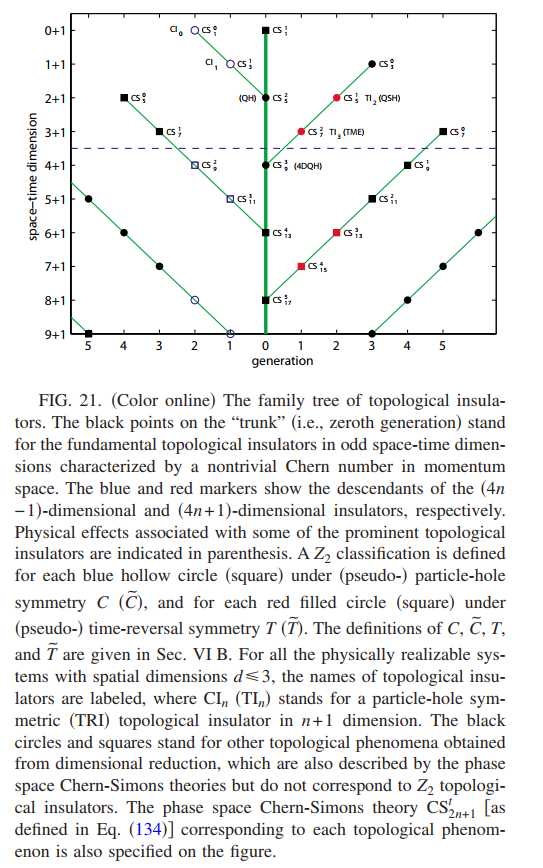
到现在为止已经系统的研究了几种相互关联的拓扑相,包括有非平庸第一Chern数的$(2+1)$维量子Hall绝缘体,有非平庸第二Chern数的$(4+1)$维拓扑绝缘体,以及它们对应的维度约化情况.可以发现$(2+1)$和$(4+1)$维都可一个基本的整数表征,分别是第一Chern数和第二Chern数.在离散对称性下($(2+1)$维粒子空穴对称,$(4+1)$维时间反演对称),$Z_2$拓扑分类可以对维度更低的系统进行定义,其对应的物理性质也可以通过对有效理论的维度约化得到,主要的性质如下图Table I所示

在这里对所有系统在想空间的统一形式进行研究.首先考虑量子Hall效应的有效模型

\[S_\text{eff}=\frac{C_1}{4\pi}\int d^2x\int dt A_\mu\epsilon^{\mu\nu\tau}\partial_\nu A_\tau\]

将第一Chern数展开可以得到

\[S=\frac{C_1}{4\pi}\int\frac{d^2k}{2\pi}\epsilon^{ij}\text{Tr}[\partial_ia_j]\int d^2xdt \epsilon^{\mu\nu\rho}A_\mu\partial_\nu A_\rho\label{ha41}\]

这里的$ij=1,2$在动量空间中,$\mu,\nu,\rho=0,1,2$是时空索引.$A_\mu,a_i$分别是实空间中的外电磁场和动量空间中的Berry位相规范场.求迹(Tr)是对所有占据态进行的.定义相空间坐标$\mathbf{q}=(t,x,y,k_x,k_y)$和想空间规范势$\mathbf{A}=(A_0,A_1,A_2,0,0),\mathbf{a}=(0,0,0,a_1,a_2)$,上面的作用量等价于下面的第二Chern-Simons项

\[S_{2+1}=\frac{1}{8\pi^2}\int d^5q\epsilon^{ABCDE}A_A\partial_BA_C\text{Tr}[\partial_Da_E]\]

这里所有的大写字母索引遍历所有相空间坐标.因为在一个系统中$\mathbf{A}$和$\mathbf{a}$总是相互正交的,这样的一个重新编写公式是平庸的,但是这对考虑维度约化是很有帮助的.比如在由$(2+1)$维系统像$(1+1)$维进行维度约化,将$k_y+A_y$替换成参数$\theta(x,t)$,它一般都是时空依赖的.这个改变包含四个方面:

• $A_y$被替换成$\theta(x,t)-\theta_0,\theta_0$扮演了$k_y$的角色
• $\partial/\partial_y$替换成$\partial/\partial\theta$
• Berry位相规范场$a_{k_y}^{\alpha\beta}=-i\langle\alpha;\mathbf{k}\rvert\partial_{k_y}\rvert\beta;\mathbf{k}\rangle$替换成$a_\theta^{\alpha\beta}=-i\langle\alpha;k_x,\theta\rvert\partial_\theta\rvert\beta;k_x,\theta\rangle$
• 积分$\int dy$和$\int dk_y/2\pi$被移出有效作用量中国

利用这些替换之后就可以得到$(1+1)$维的有效作用量.下面来展示如何推导$(1+1)$为有效理论,从(\ref{ha41})出发,在维度约化之后规范场$A_\mu$仅依赖于$(1+1)$维的坐标$(t,x)$,在Chern-Simons形式$\epsilon^{\mu\nu\tau}A_\mu\partial_\nu A_\tau$中包含$\partial_y$的项恒等于零,因此

\[\epsilon^{\mu\nu\tau}A_\mu\partial_\nu A_\tau=2(A_t\partial_xA_y-A_x\partial_tA_y)=2(A_t\partial_x\theta-A_x\partial_t\theta)\]

在分部积分之后有,效作用量(\ref{ha41})经过上面的替换后表示为

\[S_{1+1}=\frac{1}{2\pi}\int dk_x\text{Tr}[\partial_{k_x}a_\theta-\partial_\theta a_{k_x}]\int dtdx(A_t\partial_x\theta-A_x\partial_t\theta)\label{5}\]

存在一个时间依赖的平滑$\theta(x,t)$场,本征态$\rvert\alpha;k_x,\theta\rangle$可以认为是时空依赖的本征态,它的空间依赖来源于$\theta(x,t)$.这种方式下,每个态$\rvert\alpha;k_x,\theta(x,t)\rangle=\rvert;k_x,x,t\rangle$是定义在整个相空间$(t,x,k_x)$中的,贝利位相规范场可以获得一个实空间的分量$a_\mu^{\alpha\beta}=-i\langle\alpha k_x;x,t\rvert\partial_\mu\rvert\beta,k_x,x,t\rangle=a_\theta\partial_\mu\theta,\mu=t,x$.同样的$a_{k_x}$的时空求导为$\partial_\mu a_{k_x}=\partial_\theta a_{k_x}\partial_\mu\theta$,利用缩写后可以将有效作用量简化为

\[S_{1+1}=\frac{1}{2\pi}\int dk_x\int dtdx\{A_t\text{Tr}[\partial_{k_x}a_x-\partial_xa_{k_x}]-A_x\text{Tr}[\partial_{k_x}a_t-\partial_ta_{k_x}]\}\]

将规范势$(A_t,A_x)$的定义一般化到位相空间矢量$(A_t,A_x,0)$,上面的方程可以表示为位相空间中的混合Chern-Simons项

\[S_{1+1}=\frac{1}{2\pi}\int d^3q\epsilon^{ABC}A_A\text{Tr}[\partial_BA_c]\]

它描述了一个非均匀的$(1+1)$维绝缘体.动量求导作用在$(A_t,A_x)$上为零.这个相空间的体系仅仅适用于当$\theta$的时空变化是光滑的,在$(t,x,y)$附近近似是个常数才是用.定量的来说,$\theta(x,y,t)$特征频率$\omega$和波矢$k$满足

\[\hbar\omega,\quad\hbar vk << E_g \label{ha45}\]

在条件(\ref{ha45})限制下$\theta$场的时空变化并不会产生越过能隙的激发,系统可以看做是由局域哈密顿量$h(k_x;x,t)$描述的能带绝缘体.

再多进行一次维度约化就可以得到$(0+1)$为的作用量,在(\ref{5})中$a_x=0,\partial_xa_{k_x}=0$,因为在维度约化之后这里没有什么是随着$x$坐标变化的,下面将$A_x$替换成参数$\phi(t)-\phi_0$有

\[S_{0+1}=-\int dt(\phi-\phi_0)\text{Tr}[\partial_\phi a_t-\partial_t a_\phi]=-\int dt\text{Tr}(\partial_t\phi\tilde{a}_\phi+\tilde{a}_t)\]

这里积分$\int dxdk_x/2\pi$已经被移除.为了后面的方便$a_t,a_{k_x}$在$(1+1)$维中与$\tilde{a_t},\tilde{a}_\phi$相关,为了得到第二个式子,进行分部积分即可.最终$(0+1)$维系统的Berry位相规范势由两部分组成

\[a^{\alpha\beta}_t=-i\langle\alpha;t,\phi(t)\rvert\partial_t\rvert\beta;t,\phi(t)\rangle$=-i\langle\alpha;t,\phi\rvert[(\frac{\partial}{\partial t})_\phi+\frac{\partial\phi}{\partial t}(\frac{\partial}{\partial\phi})_t]\rvert\beta;t.\phi\rangle=\tilde{a}_t+\partial_t\phi\tilde{a}_\phi\]

结合上面的两个方程之后可以得到

\[S_{0+1}=-\int dt\text{Tr}[a_t]\]

在这种情况下唯一保持规范不变的量是通过绝热演化路径得到的单粒子系统的Berry位相.

对于第二族的拓扑绝缘体,有效理论

\[S_\text{eff}=\frac{C_2}{24\pi^2}\int d^4xdt\epsilon^{\mu\nu\rho\sigma\tau}A_\mu\partial_\nu A_\rho\partial_\sigma A_\tau\]

在相空间可以表示为

\[S_{4+1}=\frac{1}{192\pi^4}\int d^9q\epsilon^{ABCDEFGHI}A_A\partial_B A_C\partial_DA_E\text{Tr}[D_Fa_GD_Ha_I]\label{7}\]

这里的协变微分为$D_B=\partial_B+ia_B$是为了非阿贝尔Berry位相规范场引入的.与前面相似的方式进行$(3+1)$维的维度约化,将第四个空间维度记为$w$,它将会被进行维度约化,之后任何$\partial_w,a_w$都将会消失,(\ref{7})中不消失的之后那些$A_w$项,现在将会被参数$\theta(x,y,z,t)$替换,另一方面在形式$D_Fa_GD_Ha_I$中的一个$F,G,H,I$会是$k_w$,现在被替换为$\theta$,最终可以得到

\[S_{3+1}=\frac{3}{96\pi^3}\int d^7q\epsilon^{\mu\nu\sigma\tau}\epsilon^{ijk}A_\mu\partial_\nu A_\sigma\partial_\tau\theta\text{Tr}[D_\theta a_iD_ja_k+\text{cycl.}]\]

$\mu,\nu,\cdots=0,1,2,3; i,j,k=1,2,3$分别是$(3+1)$维中的时空和动量指标,cycl.带脖啊的是$\theta,ij,k$对应的轮换项.积分$\int dk_wdw/2\pi$已经被移除,前面的因子3来源于这里由三个$A_A$.同样的在$(2+1)$维向$(1+1)$维进行时,$\partial_\mu\theta D_\theta$被替换为$D_\mu$,最终可以得到$(3+1)$维绝缘体的结果

\[\begin{align} S_{3+1}=\int\frac{d^7q}{32\pi^3}\epsilon^{AB\cdots G}A_A\partial_BA_c\text{Tr}[D_Da_ED_Fa_G]\label{ha45} \end{align}\]

根据$P_3$的定义

\[P_3(\theta_0)=\int d^3k\mathcal{K}^\theta=\frac{1}{16\pi^2}\int d^3k\epsilon^{\theta ijk}\text{Tr}[(f_{ij}-\frac{1}{3}[a_i,a_j])\cdot a_k]\]

可知

\[\partial_l P_3=\frac{1}{8\pi^2}\int d^k\epsilon^{\theta ijk}\text{Tr}[f_{li}f_{jk}]\]

从上面$(2+1)$维$\rightarrow(1+1)$维$\rightarrow(0+1)$维和$(4+1)$维$\rightarrow(3+1)$维$\rightarrow(2+1)$维的研究,可以在相空间找到一个一般的规则来实现维度约化的相空间Chern-Simons理论.对于一个$(d+1)$维的系统,想空间维度为为$2d+1$,对应相空间Chern-Simons维度约化定义如下:

• 从作用量中移除$\partial_AA_B$项并且替换$(2d+1)$维的反对称张量为$(2d-1)$维
• 当$x_d,k_d$是空间维度时移除积分$\int dx_ddk_d/2\pi$并且动量指标被约化
• 当外部规范场$A_A$的幂次为$n$时乘以一个因子$n$

根据上面的规则,$(2+1)$维TRI绝缘体的有效作用量可以从(\ref{ha45})再进行一次维度约化得到

\[S_{2+1}=\int \frac{d^5q}{8\pi^2}\epsilon^{ABCDE}A_A\text{Tr}[D_Ba_CD_Da_E]\]

这里的系数由$8\pi^2=32\pi^2/(2\cdot 2\pi)$决定.

对于$(2n+1)$维的拓扑绝缘体其有效理论为

\[S_{2n+1}=\frac{C_n}{(n+1)!(2\pi)^n}\int d^{2n+1}x\epsilon^{\mu_1\mu_2\cdots\mu_{2n+1}}A_{\mu_1}\partial_{\mu_2}A_{\mu_3}\cdots\partial_{\mu_{2n}}A_{\mu_{2n+1}}\]

这里的第$n$Chern数在动量空间中的定义为

\[C_n=\frac{1}{n!2^n(2\pi)^2}\int d^{2n}k\epsilon^{i_1i_2\cdots i_{2n}}\text{Tr}[f_{i_1i_2}f_{i_3i_4}\cdots f_{i_{2n-1}i_{2n}}]\]

对于$(4n+1)$维相空间有效作用量的公式为

\[S_{4n+1}=\frac{1}{n!(n+1)!(2\pi)^{2n}}\int d^{4n+1}q\epsilon^{A_1A_2\cdots A_{4n+1}}A_{A_1}\partial_{A_2}A_{A_3}\cdots\partial_{A_{2n}}A_{A_{2n+1}}\text{Tr}[D_{A_{2n+2}}a_{A_{2n+3}}\cdots D_{A_{4n}}a_{A_{4n+1}}]\label{ha47}\]

根据维度约化的一般规则,可以得到低纬度拓扑绝缘体的有效理论,它是拓扑理论(\ref{ha47})的”子孙”.

从上面的实例中可以看到,在维度约化的过程中,Berry位相规范势$a_i$的数目在有效作用量中是不变的,尽管在每一步约化中外部规范势$A_\mu$是减少的.在经过$n+1$次约化之后,可以得到维度为$[(n-1)+1]$维的系统,此时不包含$A_i$.就像$(0+1)$维系统,有效作用量的变分并不导致任何对系统的响应,而只是由绝热演化时候的Berry位相来描述.很明显,为杜月华不能再对这个$[(n-1)+1]$维的系统进行,存在非平庸第$n$Chern数的$(2n+1)$维拓扑绝缘体在维度约化中仅有$(n+1)$个”子孙”.

这儿离来看一下一个$(2n+1)$维拓扑绝缘体的第$m$个子孙$1\leq m\leq n+1$

\[S^{m}_{2n+1-m}=\frac{\begin{array}{c}2n+1-m\\ n\end{array}}{(2n+1-m)!}\int\frac{d^{4n+1-2m}}{(2\pi)^{2n-m}}\epsilon^{A_1A_2\cdots A_{4n+1-2m}}A_{A_1}\partial_{A_2}A_{A_3}\cdots\partial_{A_{2n-2m}}A_{A_{2n+1-2,}}\text{Tr}[D_{A_{2n+2-2m}}a_{A_{2n+3-2m}}\cdots D_{A_{4n-2m}}a_{A_{4n+1-2m}}]\\ \equiv CS_{4n-2m+1}^{n-m+1}\]

$CS_s^t$代表的是混合的Chern-Simons作用量在$s$相空间维度对应的外场$A_A$的幂指数是$t$.特别的,$CS_s^0$是Berry位相规范场$a_A$的纯非阿贝尔Chern-Simons项,它不能通过函数$f_{AB}=D_Aa_B-D_Ba_A$单独约化得到.在给定空间维度$d$,在能带绝缘体所有可能的拓扑现象都由$CS_{2d+1}^t$取所有可能的$t$值所给出.这里需要注意,外部规范场$A_A$仅在实空间中给出,所以当$A$或者$B$是动量所以的时候$A,B=d+2,d+3,\cdots,2d+1$,$A_A,\partial_BA_A$都是为零.

因为在$CS_{2d+1}^t$中又t$t$个$A_A$,至少可以在$A_A$上作用$t-1$次偏微分,当$2t-1>d+1$的时候Chern-Simons项$CS_{2d+1}^t$就会消失,所以在一个$(d+1)$维的相空间中,总共会有$[d/2]+2$个科艺隆的Chern-Semions项,它们是$CS^t_{2d+1},t=0,1,\cdots,[d/2]+1$.

对$(2+1)$维系统,总共有3个可以利用的相空间Chern-Simons项,其中$CS_5^2$描述量子Hall绝缘体,$CS_5^1$描述量子自旋霍尔绝缘体,第三个为

\[CS_5^0=\frac{3!(2\pi)^2}{1}\int d^5q\epsilon^{ABCDE}\text{Tr}[a_A\partial_Ba_C\partial_Da_E+\frac{3}{2}a_Aa_Ba_c\partial_Da_E+\frac{3}{5}a_Aa_Ba_ca_Da_E]\]

这里并不包含$A_A$,因此不能描述任何体系对电磁场的响应性质.将上面的所有内容组合起来就可以得到下面的家族表

对于一个$(n+1)$维系统由$N$个占据态,在相空间中可以定义一个$U(N)$的规范矢势

\[\mathcal{A}^\lambda_A=\lambda A_A=a_A\]

$A_A$是外场,$a_A$是Berry位相规范势,$\mathcal{A}_A^\lambda$的非阿贝尔Chern-Simons项为

\[CS_{2n+1}(\lambda)\equiv CS_{2n+1}[\mathcal{A}^\lambda_A]=\frac{1}{(n=1)!(2\pi)^n}\int d^{2n+1}q\epsilon^{A_1A_2\cdots A_{2n+1]}}\text{Tr}[\mathcal{A}_{A_1}^\lambda\partial_{A_2}\mathcal{A}_{A_3}^\lambda\cdots \partial_{A_{2n}}\mathcal{A}_{A_{2n+1}}^\lambda+\text{N.T.}]\]

这里$\text{N.T}$表示包含对易$\mathcal{A}A^\lambda$的非阿贝尔项.它可以由$(2d+1)$维的Chern-Simons像是到$[(2d+1)+1]$维的Chern形式决定. 将作用量$CS{2n+1}(\lambda)$根据$\lambda$展开,得到下面的方程

\[CS_{2n+1}(\lambda)=\sum_{t=0}^{[n/2]+1}\lambda^tCS_{2n+1}^t\rightarrow SC_{2n+1}^t=\frac{1}{t!}\frac{\partial^t}{\partial\lambda^t}CS_{2n+1}(\lambda)\rvert_{\lambda=0}\]

着意味着所有可能想空间Chern-Simons项都可以从单个生成泛函$CS_{2n+1}(\lambda)$得到.

一般维度的$Z_2$拓扑绝缘体

对$(2+1)$维和$(4+1)$维的绝缘体,在离散对称性的限制下可以定义$Z_2$不变量,$(2+1)$维绝缘体的”子孙”,在粒子空穴对称限制下定义了$Z_2$不变量,哈密顿量满足

\[C^\dagger h(-{\bf k})C=-h^T(\mathbf{k}),\quad C^\dagger C=C^*C=\mathbb{I}\]

这个分类的关键点是在两个粒子空穴对称哈密顿量$h_1(k),h_2(k)$中找到一个插值,当结合其粒子空穴变换的伙伴后可以形成一个闭合的路径.这样一个闭合路径的Chern数总是对应着确定的宇称,并不依赖于路径的选择.同样的,对于$(0+1)$维满足粒子空穴对称的系统也可以定义$Z_2$分类.对于$(4+1)$维绝缘体这个过程是相同的,只不过此时的粒子空穴对称替换成了时间反演对称

\[T^\dagger h(-\mathbf{k})T=h^T(\mathbf{k}),\quad T^\dagger T=-T^*T=\mathbb{I}\]

根据这个可以将$\mathbb{Z_2}$分类推广到高维度.,首先来理解$(2+1)$维与$(4+1)$维所需要的的不同的离散对称性.最简单的方式是研究 Chern-Simons理论在粒子空穴对称(C)和时间反演对称(T)操作下的不同.

只在粒子空穴对称下,电荷密度和电流都改变符号,矢势同样也是这样,因为是受到最小耦合$A_\mu j^\mu$不变形的原因.

同样的也可以得到$A_\mu$在时间反演下的性质

\[C:A_\mu\rightarrow -A_\mu,\quad T:A_\mu\rightarrow\left\{\begin{arrar}{c}A_0\\ -A_i\end{array}\right.\]

在$C$和$T$的操作下,动量算符$-i\partial_\mu$具有和$A_\mu$相同的性质.基于这些,Chern-Simons拉格朗日量的变换性质为

\[C:S_{2n+1}^{CS}\rightarrow (-1)^{n+1}S_{2n+1}^{CS},\quad T:S_{2n+1}^{CS}\rightarrow (-1)^nS_{2n+1}^CS\]

可以看到$S_{4n+1}^{CS}$在T的操作下是偶的,在C的操作下是奇的,而$S_{4n-1}^{CS}$在T的操作下是奇的,在C的操作下是偶的.总之,一个$(4n+1)$维拓扑绝缘体必须破坏粒子空穴对称但是满足时间反演对称,就像$(4+1)$维的情况;一个$[(4n-2)+1]$维的拓扑绝缘体必须破坏时间反演对称但满足粒子空穴对称,就像$(2+1)$维的情况.总而言之,$(4n+1)$维[(4n-1)维]拓扑绝缘体的”子孙”,只有在时间反演对称(粒子空穴对称)的限制下才可能定义$Z_2$分类.

前面介绍的通过维度约化定义$Z_2$分类的过程看起来可以递归的运用到所有$(2n+1)$维拓扑绝缘体上,然而这个结论是不正确的.比如可以研究$(1+1)$维TRI绝缘体作为$(2+1)$维量子自旋霍尔绝缘体的”子孙”[不是$2+1$维量子Hall绝缘体].在从$(3+1)$维向$(2+1)$维的维度约化过程中,在两个$(2+1)$维TRI哈密顿量$h_1(\mathbf{k}),h_2(\mathbf{k})$中插入$h(\mathbf{k},\theta)$.当$h(\mathbf{k},\theta)$要求满足时间反演对称的时候,它对应的正是$(3+1)$维拓扑绝缘体,此时定义了$Z_2$拓扑量$N_3[h(\mathbf{k},\theta)]$,它并不依赖于插值$h(\mathbf{k},\theta)$的路径选择,从而提供了一个判断$h_(\mathbf{k}),h_2(\mathbf{k})$是否拓扑等价的一个判据.如果对$(1+1)$维系统执行同样的过程,看起来对于两个哈密顿量$h_1(k),h_2(k)$可以以相同的方式定义$Z_2$拓扑分类.这个结论是否正确,以一个格点Dirac模型为例进行研究,$(2+1)$维$4\times 4$的单粒子格点Dirac模型存在时间反演对称可以表示为

\[h_{2D}(\mathbf{k})=\Gamma^1\sin k_x\Gamma^2\sin k_y+\Gamma^0[m+c(\cos k_x+\cos k_y)]\label{9}\]

当$0 < m < 2\rvert c\rvert$或者$-2\rvert c\rvert < m < 0$的时候是个拓扑非平庸的相. 拖过维度约化,$h_{2D}(\mathbf{k})$可以认为是$(1+1)$维TRI哈密顿量两个$h_1(k)=h_{2D}(k,0),h_2(k)=h_{2D}(k,\pi)$之间的插值.如果$Z_2$的定义过程可以适用,当(\ref{9})是非平庸的时候,那么$h_1,h_2$应该是拓扑不等价的.总而言之,不可能在$h_1,h_2$之间定义另外一个插值$h_0(k,\theta)$,使得其满足

\[T^\dagger h_0(k,\theta)T=h^*_0(-k,-\theta)=h^*_0(-k,\theta),\quad\text{对任意的}\quad\theta\]

然而这样的插值在此时是可以构建的,如下

\[h_0(k,\theta)=\Gamma^1\sin k+\Gamma^{02}\sin^2\theta+\Gamma^0(m+c\cos k_x+c\cos \theta),\quad \Gamma^{02}=i\Gamma^0\Gamma^2\]

$\Gamma^{02]$在时间反演下是偶的.这里存在两个拓扑不等价的插值$h_0(k,\theta)$和$h_{2D}(k,\theta)$说明对于$(1+1)$维TRI绝缘体,不能以在$(2+1)$维和$(3+1)$维相同的方式取定义$Z_2$拓扑分类.

这个方法的失败主要是因为参数化哈密顿量的流形是简单连接的,换句话说,一个插值$h(\mathbf{k},\theta,\varphi)$总是可以被定义成两个插值$h(\mathbf{k},\theta),h^{‘}(\mathbf{k},\theta)$.

在上面的额实例中,路径$h_{2D}$和$h_0$不能通过绝热的方式连接起来,因为组合路径

\[g(k,\theta)=\left\{\begin{array}{c}h_{2D}(k,\theta),\quad\theta\in[0,\pi]\\ h_0(k,2\pi-\theta),\quad\theta\in[\pi,2\pi]\end{array}\right.\]

是一个$(2+1)$维的哈密顿量,它破坏了时间反演对称且有一个非平庸的的第一Chern数$C_1=-1$.总之,路径$g$不能收缩成一个点,在定义路径无关的$Z_2$不变量的时候是失败的.

从上面的事例中可以看到,对$(2n+1)$维拓扑绝缘体的”子孙”定义$Z_2$拓扑分类在维度被约化到$[(2n-3)+1]$维的时候是失败的,因为 在$[(2n-3)+1]$维的哈密顿量而言,冰河的路径定义了一个更低的Chern数$C_{n-1}$.总而言之,$Z_2$拓扑绝缘体作为$(2n+1)$维拓扑绝缘体的”子孙”只能被定义在$[(2n-1)+1],[(2n-2)+1]$维.由于体态的拓扑绝缘体总是对应一个拓扑保护的边界态,$Z_2$分类的有效应需要通过研究边界理论的稳定性.比如第二Chern数为$C_2$的$(4+1)$维拓扑绝缘体包含$\rvert C_2\rvert$种类的手性(Weyl)费米子.

最简单的考虑格点Dirac模型

\[H=\sum_{n,i}[\psi^\dagger_n(\frac{c\Gamma^--i\Gamma^i}{2})\psi_{n+\hat{i}}+\text{H.c} +m\sum_n\psi^\dagger_n\Gamma^0\psi_n\]

在参数区间$-4c < m < -2c$边界上的单粒子哈密顿量为

\[h_{\partial(4+1)}=v\vec{\sigma}\cdot\vec{\bf p},\]

因为没有质量项可以利用,它是拓扑稳定的边界态.通过维度约化,$(3+1)$维$Z_2$非平庸绝缘体的边界理论简单的由上面的方程当$p_z=0$

\[H_{\partial(3+1)}=v(\sigma_x+\sigma_yp_y)\]

在时间反演对称下它是拓扑稳定的,因为不存在时间反演不变的质量项.同样的分析对于$(2+1)$为拓扑绝缘体为$H_{\partial(2+1)}=v\sigma_zp_z$.当维度约化再进行词义,得到$(1+1)$维系统的$(0+1)$维边界$H_{\partial(1+1)}=0$.着所描述的正是局域在边界上的Kramers对.因为这个Kramers对midgap states可以在不破坏时间反演的情况下平移常数值的能量,$(1+1)$维TRI绝缘体并没有拓扑非平庸的类.

上面边界理论的分析同样可以简单地推广到高维,具有非平庸Chern数的$[2n+1]$维拓扑绝缘体的边界态由$[(2n-1)+1]$维的手性费米子描述,哈密顿量为

\[H_{2n-1}(\mathbf{p})=v\sum_{i=1}^{2n-1}p_i\Gamma^i\label{ha49}\]

这里$\Gamma^i$是$2^{n-1}\times 2^{n-1}$维矩阵,构成了$so(2n-1)$Cliffor代数的表示.$(2n+1)$维系统的第m个”子孙”的边界理论就是取$p_i=0,i=2n-m,2n-m+1,\cdots,2n-1.$对称性及未定型可以通过研究$\Gamma^a$的性质.

• 手性哈密顿量(\ref{ha49})在不同的维度满足不同的离散对称性

\[C^\dagger H_{2n-1}(\mathbf{p})C=-H_{2n-1}(-\mathbf{p}),\quad C^*C=\mathbb{I},\quad m=4m-3,\quad m\in\mathbb{N},\\ T^\dagger H_{2n-1}(\mathbf{p})T=H_{2n-1}(-\mathbf{p}),\quad T^*T=-\mathbb{I},\quad n=4m-2,\quad m\in\mathbb{N},\\ \tilde{C}^\dagger H_{2n-1}(\mathbf{p})\tilde{C}=-H_{2n-1}(-\mathbf{p}),\quad \tilde{C}^*\tilde{C}=-\mathbb{I},\quad n=4m-1,\quad m\in\mathbb{N}\\ \tilde{T}^\dagger H_{2n-1}(\mathbf{p})\tilde{T}=H_{2n-1}(-\mathbf{p}),\quad\tilde{T}^*\tilde{T}=\mathbb{I},\quad n=4m,\quad m\in\mathbb{N}\]

• 只有$H_{2n-1}$的前两个”子孙”,$H(\mathbf{p})=\sum_{i=1}^{2n-2}p_i\Gamma^i,H(\mathbf{p})=\sum_{i=1}^{2n-3}p_i\Gamma^i$,在给定的维度和对称性下面才是稳定的($C,\tilde{C},T,\tilde{T}$).$(2n+1)$维拓扑绝缘体的”子孙”中可以存在$Z_2$拓扑非平庸绝缘体的只在$[(2n-1)+1]$维和$[(2n-2)+1]$维.

参考

• 1.Topological field theory of time-reversal invariant insulators

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。