这篇博客中利用另外一种格林函数的方法来计算拓扑绝缘体的边界态.
在前面利用格林函数求解边界态这篇博客中利用迭代格林函数的方法计算了拓扑绝缘体的边界态,但是结果中边界态的确很明显,但是体态的性质却不会表现的很清晰,这里就像利用矩阵求逆的方式,直接计算哈密顿量对应的谱函数,从而来计算边界态和体态的性质,但是这个方法的缺点也是比较明显的,那就是耗时比较长.
模型
仍然以拓扑绝缘体的哈密顿量为出发点
\[H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+\lambda_x\sin k_x\sigma_xs_z+\lambda_y\sin k_y\sigma_y\label{ham}\]对这个哈密顿量沿着$x$方向取开边界,沿$y$方向仍然是周期边界条件,这样就可以在一个圆柱结构上计算边界态了,对应的谱函数为
\[A(k,\omega)=-2\text{Im}[\omega+i\epsilon-H(\mathcal{k})]^{-1}\]这里的$H(\mathbf{k})$是开边界之后的哈密顿量.
代码
module pub
implicit none
integer yn,kn,ne,N,enn,hn
real eta,dk,de
parameter(yn = 50,hn = 4,kn = 50, ne = 50,N = yn*4,eta = 0.01,dk = 0.01,de = dk)
real,parameter::pi = 3.1415926535
complex,parameter::im = (0.,1.0)
complex Ham(N,N),one(N,N)
!=================================
real m0,mu
real tx,ty
real ax,ay,gamma
complex g1(hn,hn)
complex g2(hn,hn)
complex g3(hn,hn)
!================cheev===============
integer::lda = N
integer,parameter::lwmax = 2*N + N**2
real,allocatable::w(:)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
integer lwork
integer lrwork
integer liwork
integer info
end module pub
!================= PROGRAM START ============================
program sol
use pub
integer i1
!====空间申请==================
allocate(w(N))
allocate(work(lwmax))
allocate(rwork(1+5*N+2*N**2))
allocate(iwork(3+5*N))
!======parameter value setting =====
m0 = 1.5
mu = 0
tx = 1.0
ty = 1.0
ax = 1.0
ay = 1.0
do i1 = 1,N
one(i1,i1) = 1 !单位矩阵
end do
call main()
stop
end program sol
!=============================================================================================
subroutine main()
! Calculate edge spectrum function
use pub
integer m1,m2,i1
real kx,ky,omega,re2
complex h1(N,N),h2(N,N)
complex re1
open(30,file="openy-bhz.dat")
!-------------------------------------------------
! y-direction is open
do omega = -3.0,3.0,de
do kx = -pi,pi,dk
re1 = 0
call openy(kx)
h1 = omega*one - ham + im*eta*one
call inv(h1,h2)
do i1 = 1,N
re1 = re1 + h2(i1,i1)
end do
re2 = -2*aimag(re1)/pi/N
write(30,999)kx/pi,omega,re2
end do
write(30,*)" "
end do
close(30)
!---------------------------------------------------------------------
! x-direction is open
open(31,file="openx-bhz.dat")
do omega = -3.0,3.0,de
do ky = -pi,pi,dk
re1 = 0
call openx(ky)
h1 = omega*one - ham + im*eta*one
call inv(h1,h2)
do i1 = 1,N
re1 = re1 + h2(i1,i1)
end do
re2 = -2*aimag(re1)/pi/N
write(31,999)ky/pi,omega,re2
end do
write(31,*)" "
end do
close(31)
999 format(3f11.5)
return
end subroutine main
!======================== Pauli Matrix driect product============================
subroutine Pauli()
use pub
! TI
!=== Kinetic energy
g1(1,1) = 1
g1(2,2) = -1
g1(3,3) = 1
g1(4,4) = -1
!====== SOC-x
g2(1,2) = 1
g2(2,1) = 1
g2(3,4) = -1
g2(4,3) = -1
!====== SOC-y
g3(1,2) = -im
g3(2,1) = im
g3(3,4) = -im
g3(4,3) = im
return
end subroutine Pauli
!==========================================================
subroutine openx(ky)
use pub
real ky
integer m,l,k
call Pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hn
do l = 1,hn
Ham(m,l) = (m0-ty*cos(ky))*g1(m,l) + ay*sin(ky)*g3(m,l)
Ham(m,l + hn) = (-tx*g1(m,l) - im*ax*g2(m,l))/2
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hn
do l = 1,hn
Ham(k*hn + m,k*hn + l) = (m0-ty*cos(ky))*g1(m,l) + ay*sin(ky)*g3(m,l)
Ham(k*hn + m,k*hn + l - hn) = -tx*g1(m,l)/2 + im*ax*g2(m,l)/2
end do
end do
else
do m = 1,hn
do l = 1,hn ! k start from 1,matrix block from 2th row
Ham(k*hn + m,k*hn + l) = (m0 - ty*cos(ky))*g1(m,l) + ay*sin(ky)*g3(m,l)
Ham(k*hn + m,k*hn + l + hn) = (-tx*g1(m,l) - im*ax*g2(m,l))/2
Ham(k*hn + m,k*hn + l - hn) = -tx*g1(m,l)/2 + im*ax*g2(m,l)/2
end do
end do
end if
end do
!------------------------
call isHermitian()
! call eigsol()
return
end subroutine openx
!==========================================================
subroutine openy(kx)
use pub
real kx
integer m,l,k
call Pauli()
Ham = 0
!========== Positive energy ========
do k = 0,yn-1
if (k == 0) then ! Only right block in first line
do m = 1,hn
do l = 1,hn
Ham(m,l) = (m0-tx*cos(kx))*g1(m,l) + ax*sin(kx)*g2(m,l)
Ham(m,l + hn) = (-ty*g1(m,l) - im*ay*g3(m,l))/2
end do
end do
elseif ( k==yn-1 ) then ! Only left block in last line
do m = 1,hn
do l = 1,hn
Ham(k*hn + m,k*hn + l) = (m0-tx*cos(kx))*g1(m,l) + ax*sin(kx)*g2(m,l)
Ham(k*hn + m,k*hn + l - hn) = -ty*g1(m,l)/2 + im*ay*g3(m,l)/2
end do
end do
else
do m = 1,hn
do l = 1,hn ! k start from 1,matrix block from 2th row
Ham(k*hn + m,k*hn + l) = (m0-tx*cos(kx))*g1(m,l) + ax*sin(kx)*g2(m,l)
Ham(k*hn + m,k*hn + l + hn) = (-ty*g1(m,l) - im*ay*g3(m,l) )/2
Ham(k*hn + m,k*hn + l - hn) = -ty*g1(m,l)/2 + im*ay*g3(m,l)/2
end do
end do
end if
end do
!---------------------------------
call isHermitian()
! call eigsol()
return
end subroutine openy
!============================================================
subroutine isHermitian()
use pub
integer i,j
do i = 1,N
do j = 1,N
if (Ham(i,j) .ne. conjg(Ham(j,i)))then
open(160,file = 'hermitian.dat')
write(160,*)i,j
write(160,*)Ham(i,j)
write(160,*)Ham(j,i)
write(160,*)"===================="
write(*,*)"Hamiltonian is not hermitian"
stop
end if
end do
end do
close(160)
return
end subroutine isHermitian
!================= 矩阵本征值求解 ==============
subroutine eigSol()
use pub
integer m
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
lwork = min(2*N+N**2, int( work( 1 ) ) )
lrwork = min(1+5*N+2*N**2, int( rwork( 1 ) ) )
liwork = min(3+5*N, iwork( 1 ) )
call cheevd('V','Upper',N,Ham,lda,w,work,lwork &
,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(110,file="mes.dat",status="unknown")
write(110,*)'The algorithm failed to compute eigenvalues.'
close(110)
end if
! open(120,file="eigval.dat")
! do m = 1,N
! write(120,*)w(m)
! end do
! close(120)
return
end subroutine eigSol
!=================================================================
subroutine inv(matin,matout)
use pub
complex,intent(in) :: matin(N,N)
complex:: matout(size(matin,1),size(matin,2))
real:: work2(size(matin,1)) ! work array for LAPACK
integer::info2,ipiv(size(matin,1)) ! pivot indices
! Store A in Ainv to prevent it from being overwritten by LAPACK
matout = matin
! SGETRF computes an LU factorization of a general M-by-N matrix A
! using partial pivoting with row interchanges.
call CGETRF(N,N,matout,N,ipiv,info2)
if (info2.ne.0)then
write(*,*)'Matrix is numerically singular!'
stop
end if
! SGETRI computes the inverse of a matrix using the LU factorization
! computed by SGETRF.
call CGETRI(N,matout,N,ipiv,work2,N,info2)
if (info2.ne.0)then
write(*,*)'Matrix inversion failed!'
stop
end if
return
end subroutine inv
编译命令
ifort -mkl file.f90
绘图
因为想要看到清晰的结果,在离散撒点的时候,间隔必须很小,那么数据文件就会很大,这里推荐gnuplot绘图,
set encoding iso_8859_1
#set terminal postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1680
set output 'density.png'
#set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
unset ztics
unset key
set pm3d
set border lw 6
set size ratio 1
set view map
set xtics
set ytics
#set xlabel "K_1 (1/{\305})"
set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
set ylabel "Y"
set ylabel offset 1, 0
set colorbox
set xrange [-1:1]
set yrange [-3:3]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'openy-bhz.dat' u 1:2:3 w pm3d
绘图
gnuplot file.gnu
最后的结果为
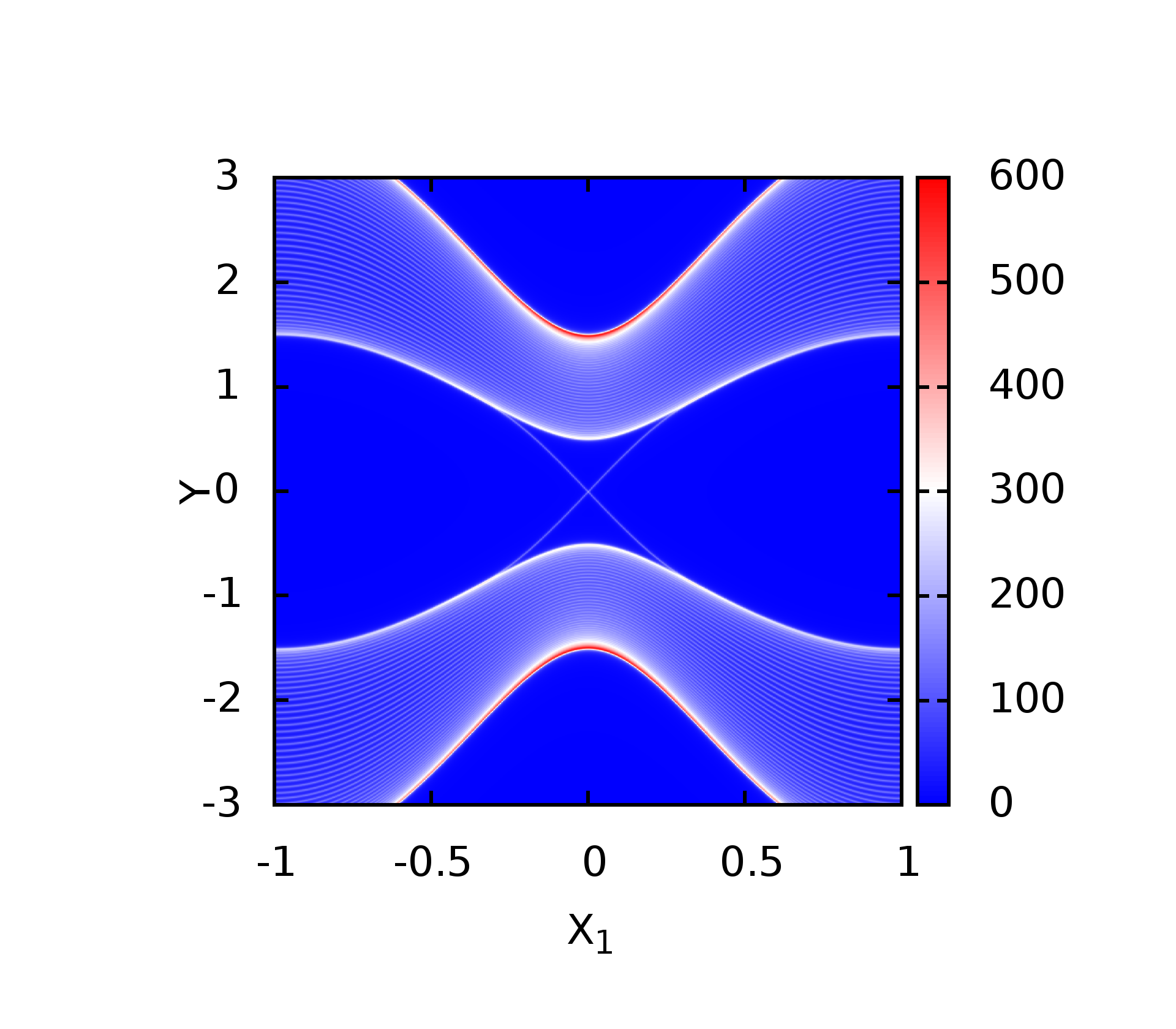
相比较于利用格林函数求解边界态中的结果,可以清晰的看到边界态和体态的结果.如果接的图中的颜色并不能很好的展现,可以在gnuplot绘图中修改颜色方案
set palette defined ( -10 "white", 0 "blue", 10 "red" )
在新的配色方案中,边界态就可以很清晰的表现出来
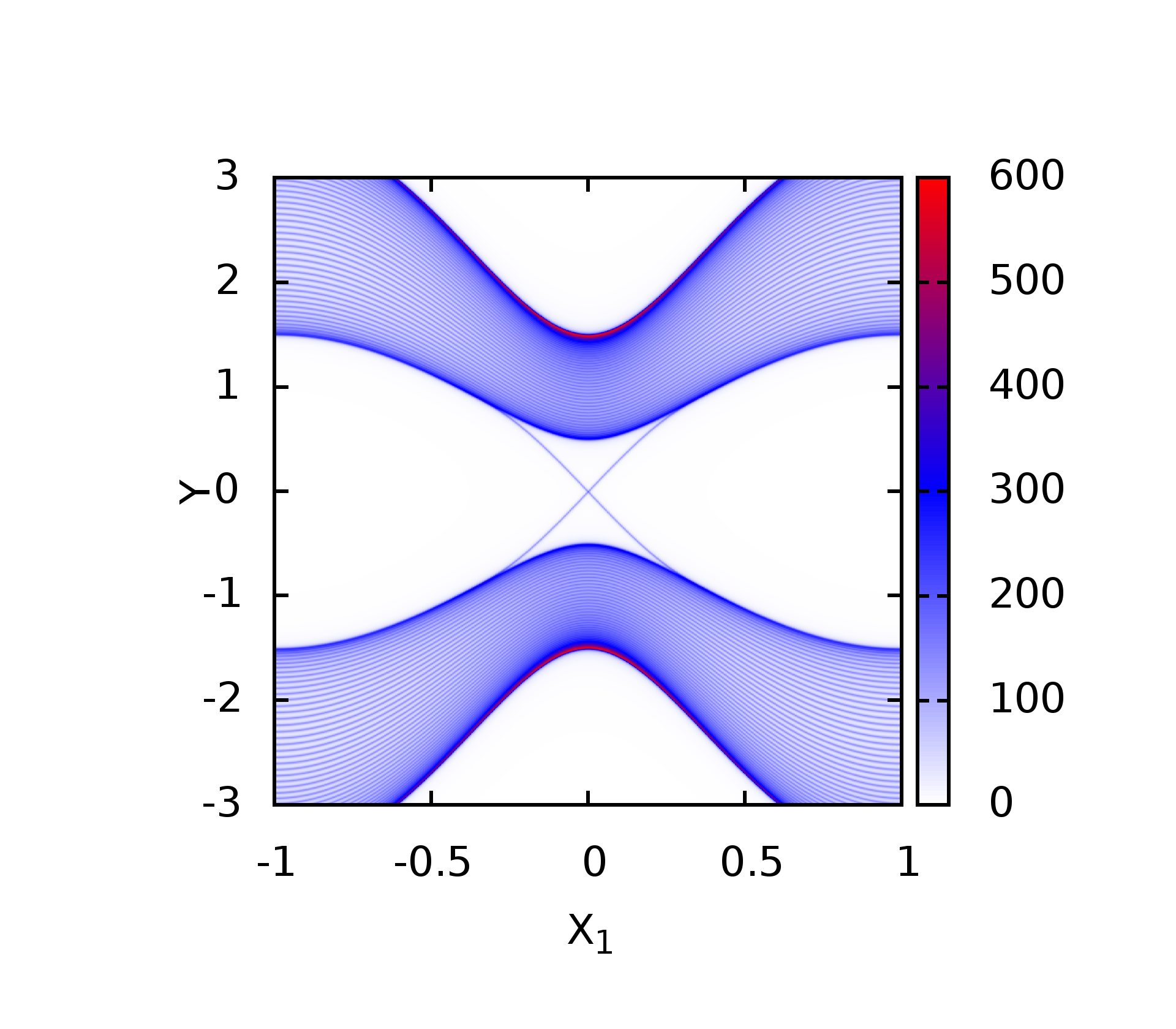
代码下载
点击这里下载代码.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |