学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.
空间群
空间群$\mathbf{G}$包含了纯平移操作${E\rvert\mathbf{t}}$,这些平移操作构成了空间群$\mathbf{G}$的一个不变子群$\mathbf{T}$.
\[\mathbf{t}=n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3\]对于实际的晶体,通常考虑周期性边界条件
\[\{E\rvert l_1N_1\mathbf{t}_1+l_2N_2\mathbf{t}_2+l_3N_3\mathbf{t}_3\}=\{E\rvert\mathbf{O}\}\]对于一个晶体,如果存在两个布拉菲点阵,那么它们之间一定是等价的,通过连续形变,一定可以将两者进行相互变换,而且在变换过程中要始终保证点阵的对称性是相同的,不能改变其对称性.下面给出14中布拉菲点阵的基矢及相关信息


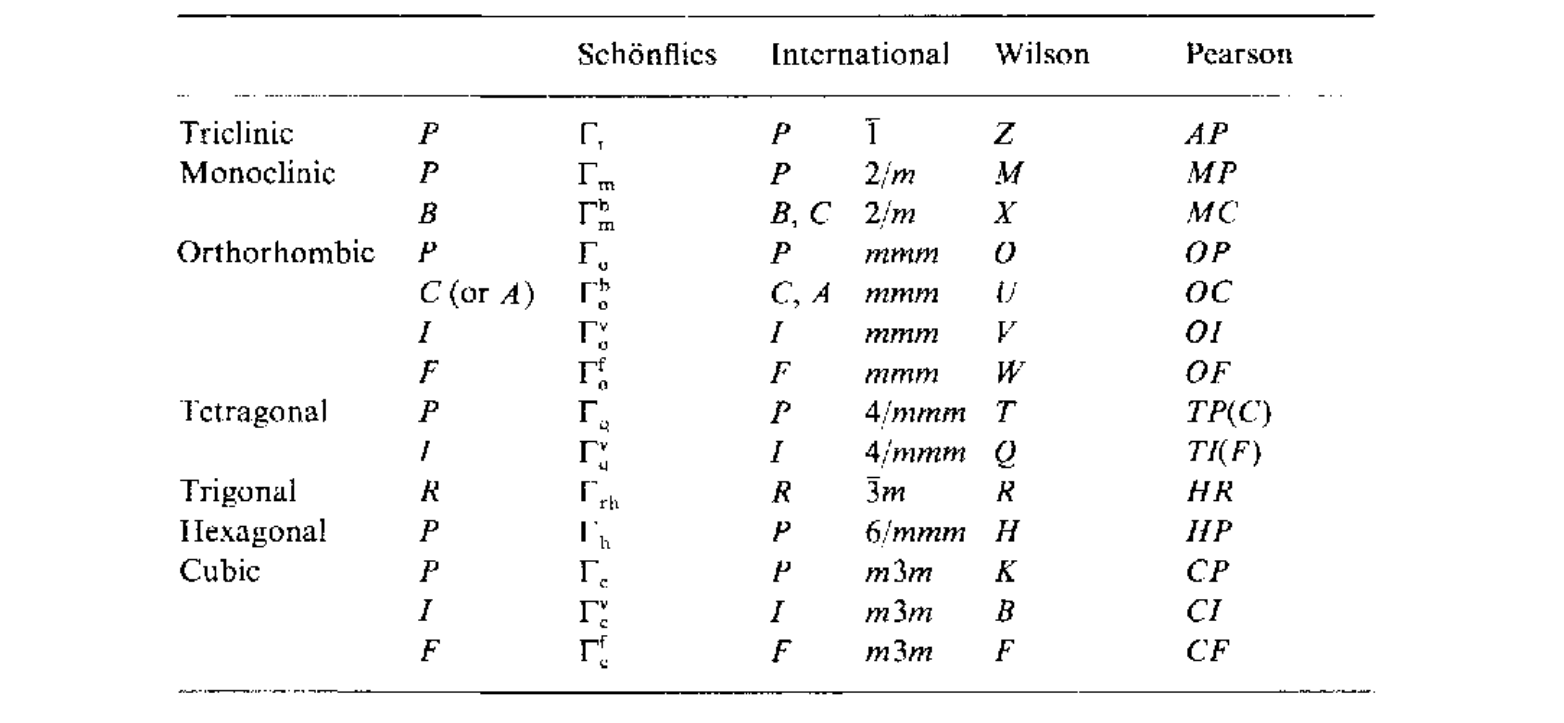
每个晶系满足的对称操作如下

下面给出每个对称操作对布拉菲点阵基矢的变换关系
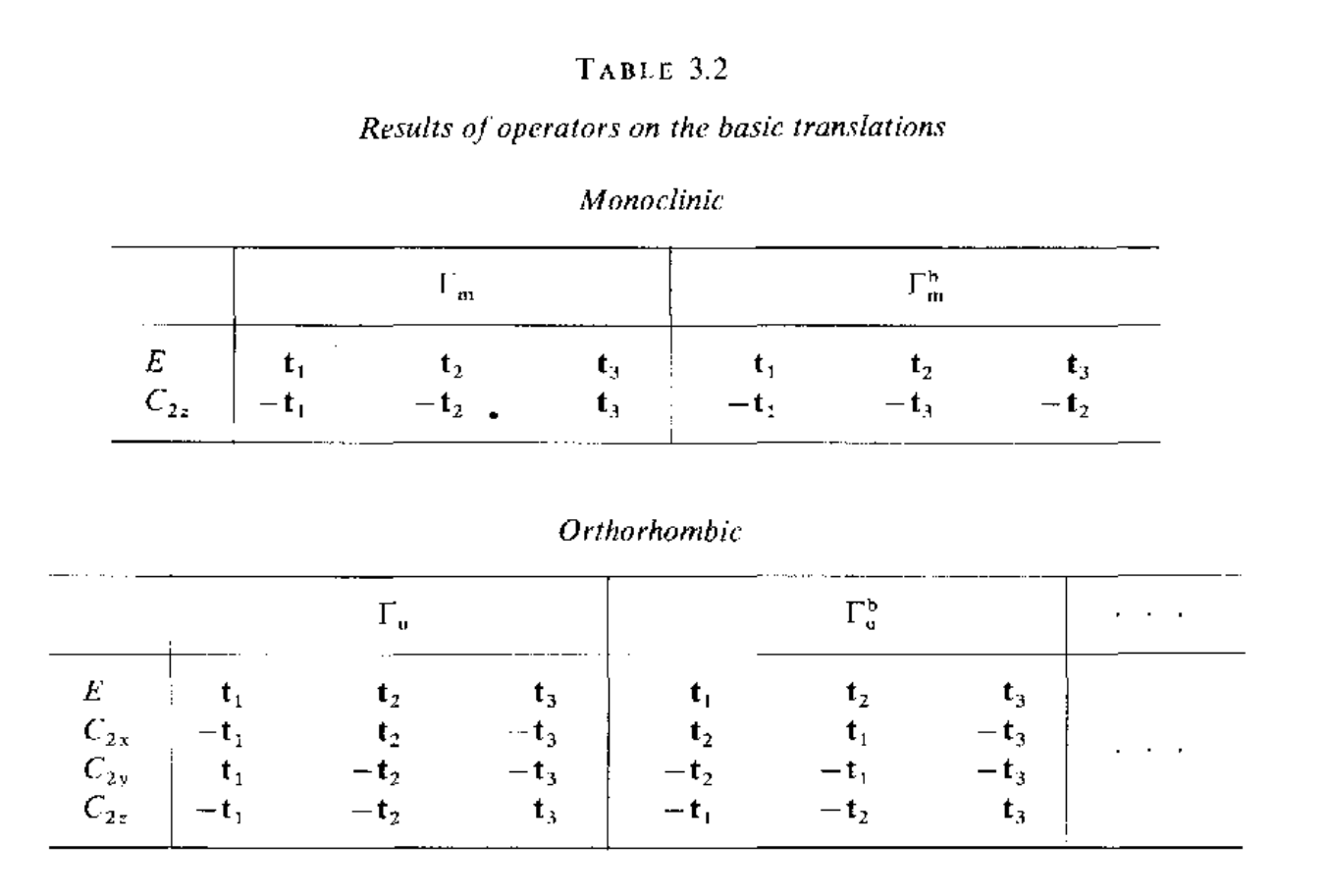
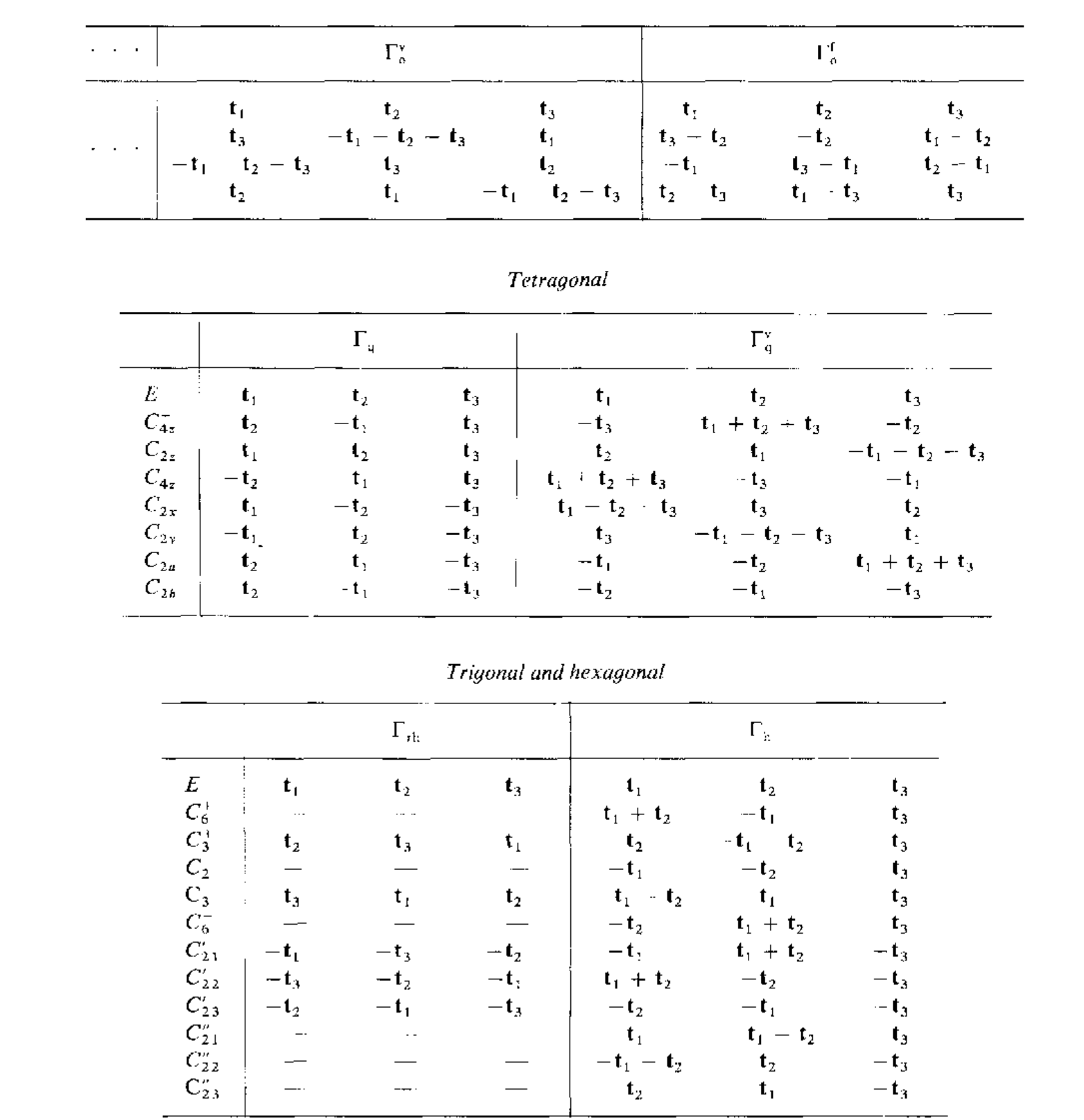
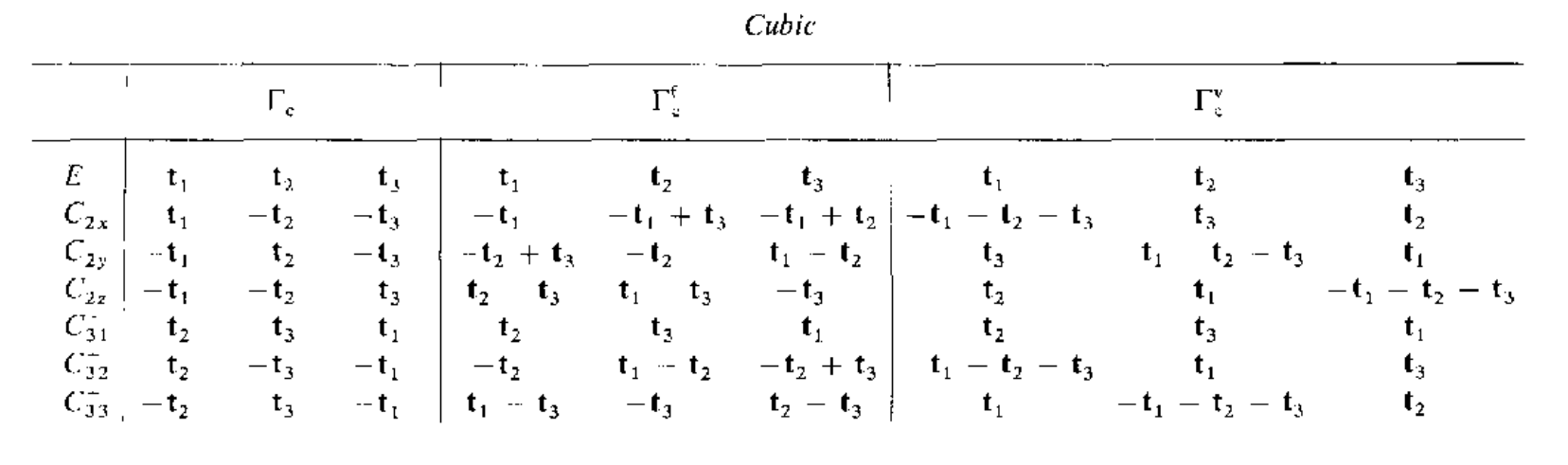
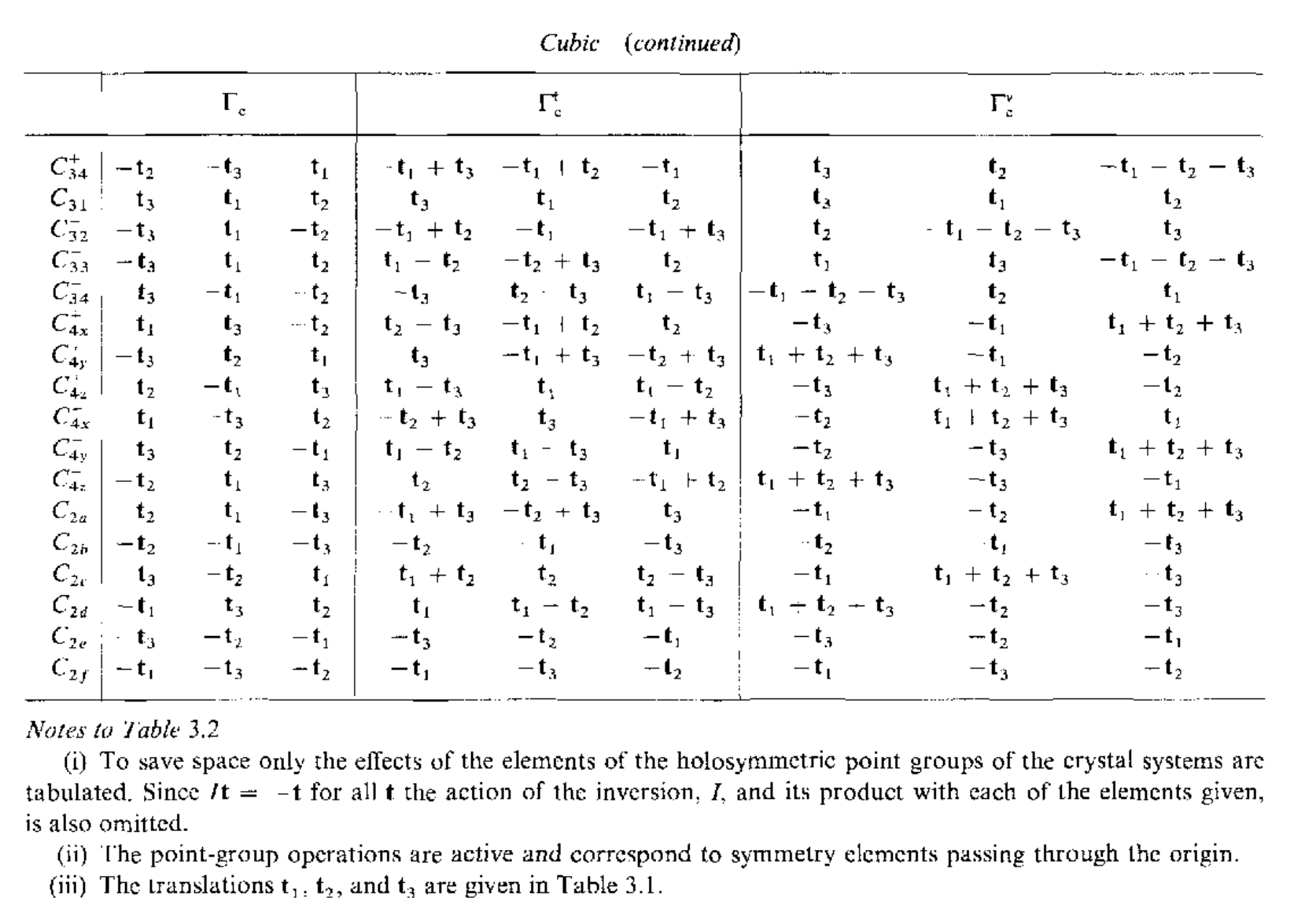
同样可以利用SpaceGroupIrep这个工具来得到具体的表
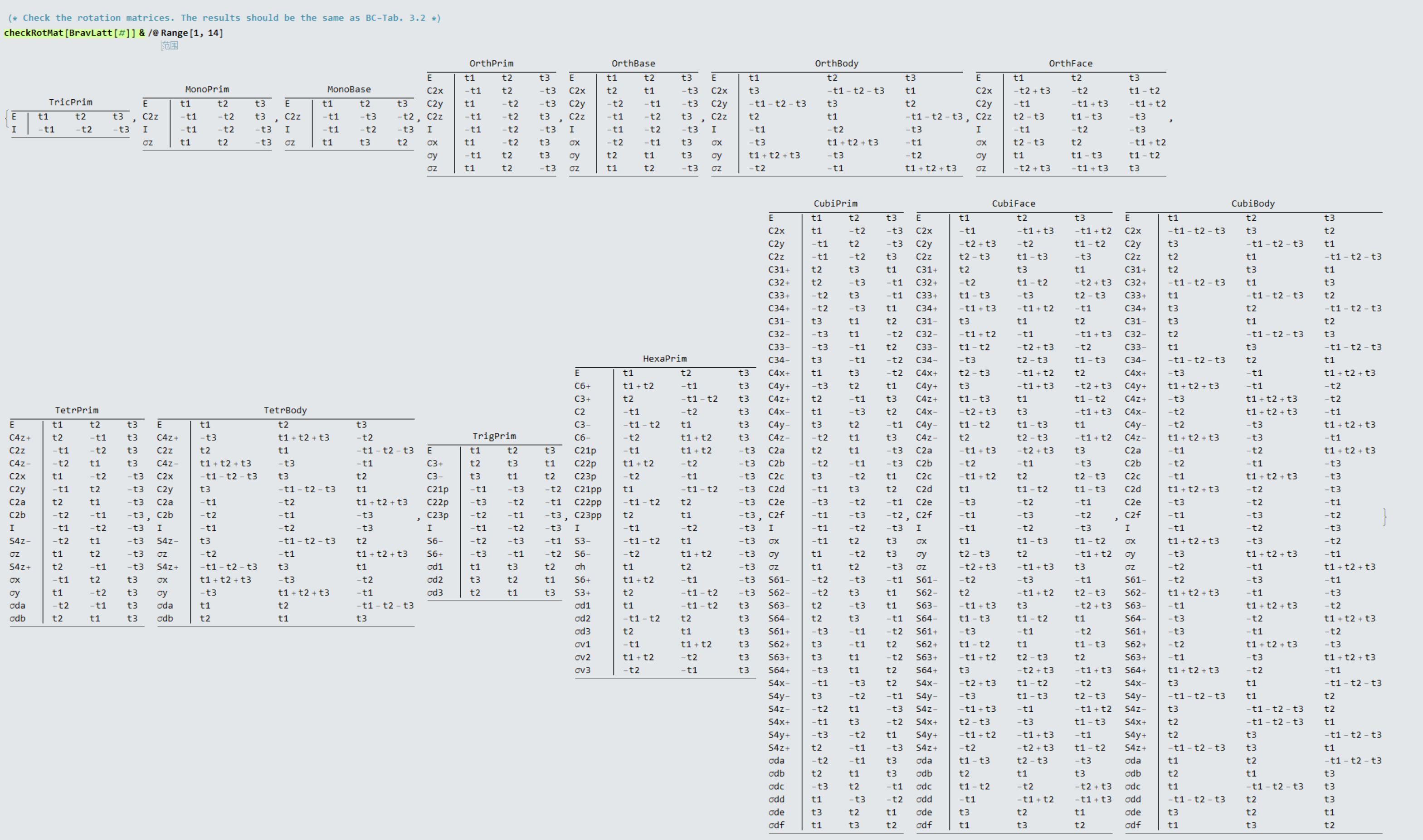
通过实空间的布拉菲点阵,同样可以定义出倒空间中的点阵
\[\mathbf{g}_i\cdot\mathbf{t}_j=2\pi\delta_{ij},\quad (i,j=1,2,3)\]利用上面的关系可以得到倒空间的基矢为
\[\mathbf{g}_1=\frac{2\pi(\mathbf{t}_2\times\mathbf{t}_3)}{\mathbf{t}_1\cdot(\mathbf{t}_2\times\mathbf{t}_3)},\quad\mathbf{g}_2=\frac{2\pi(\mathbf{t}_3\times\mathbf{t}_1)}{\mathbf{t}_2\cdot(\mathbf{t}_3\times\mathbf{t}_1)},\quad\mathbf{g}_3=\frac{2\pi(\mathbf{t}_1\times\mathbf{t}_2)}{\mathbf{t}_3\cdot(\mathbf{t}_1\times\mathbf{t}_2)}\]利用这些基矢,可以在倒空间中定义点阵
\[\mathbf{g}=n_1\mathbf{g}_1+n_2\mathbf{g}_2+n_3\mathbf{g}_3\]倒空间中的布拉菲点阵如下

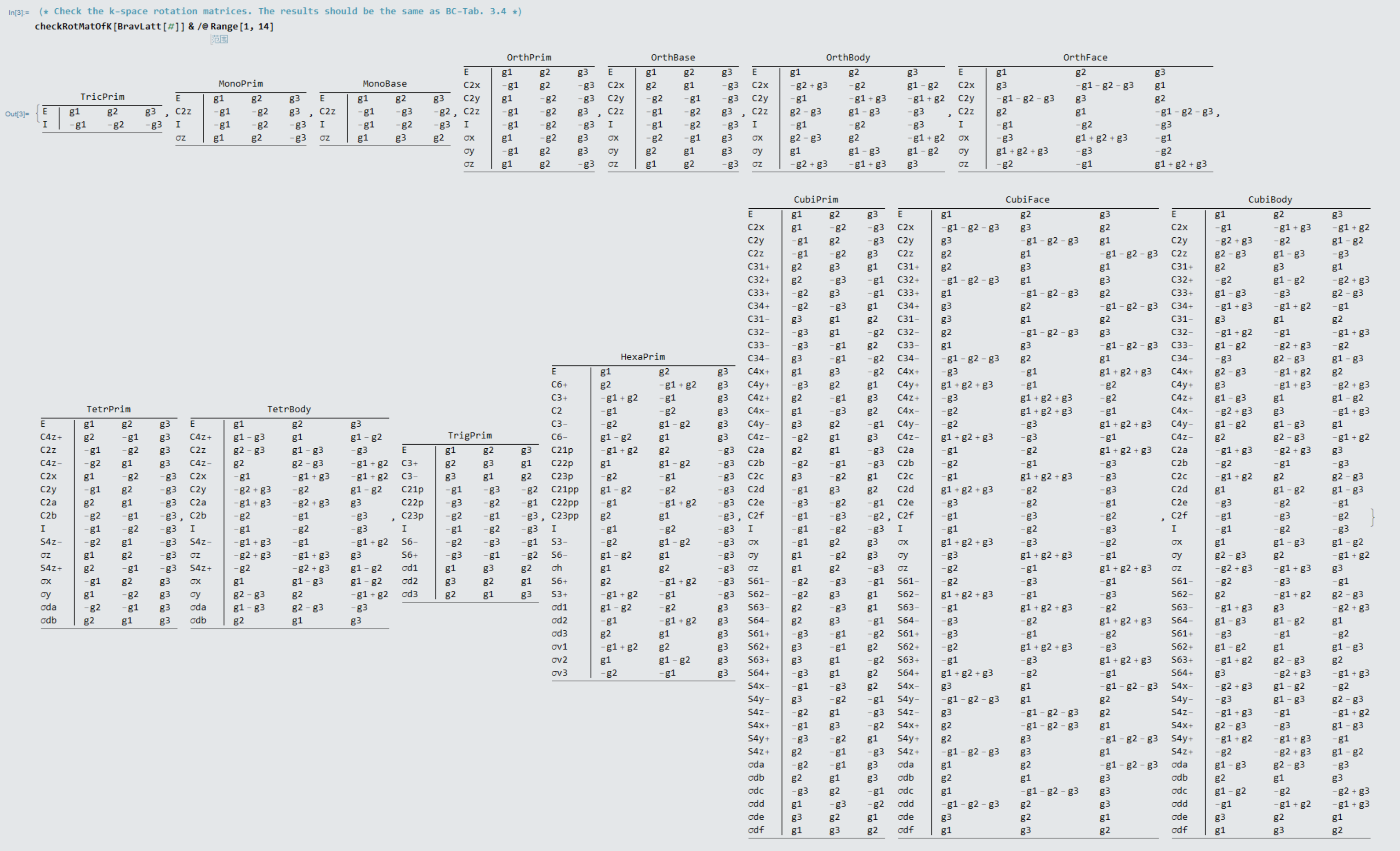
同样的也可以得到点群操作对倒空间基矢的变换关系
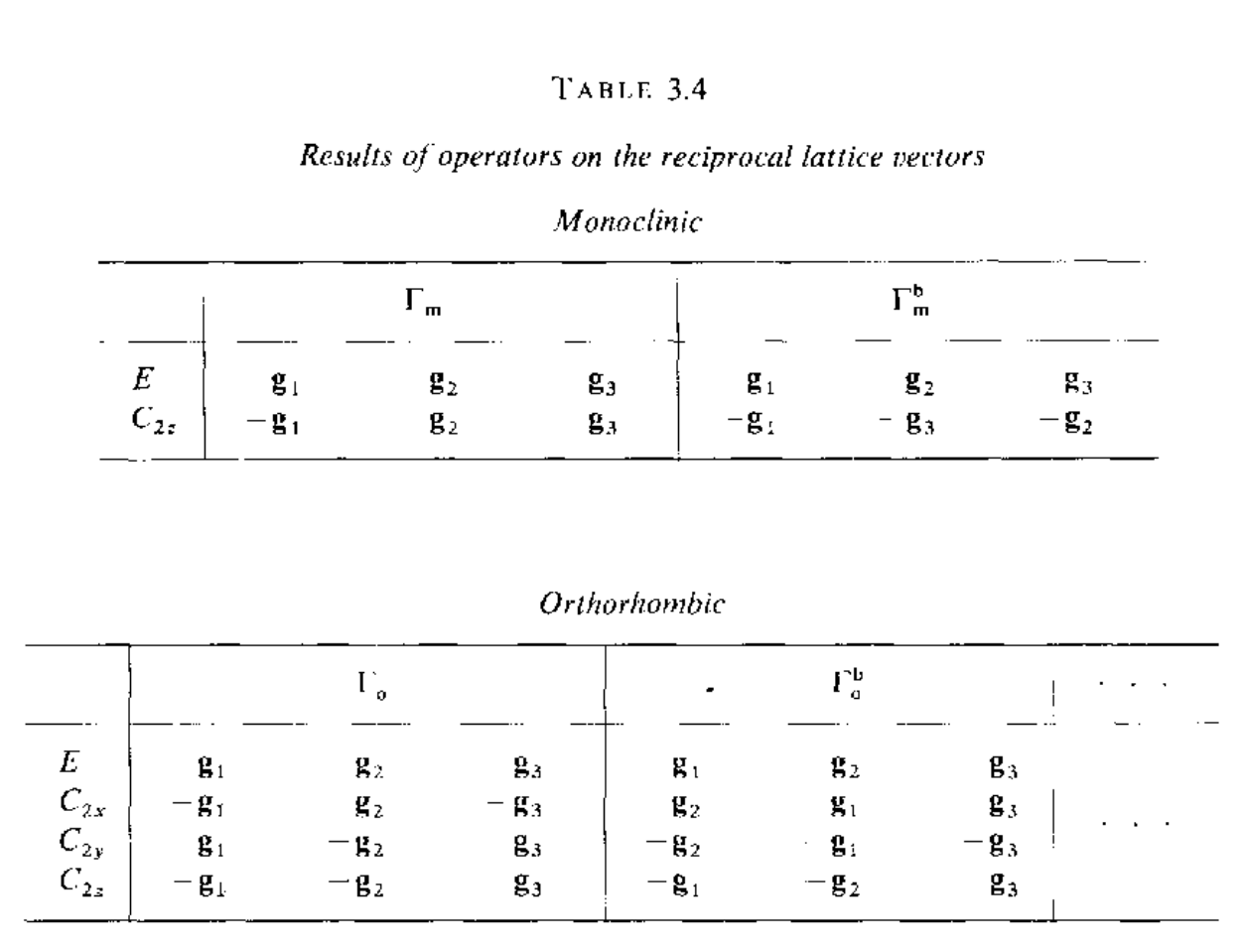
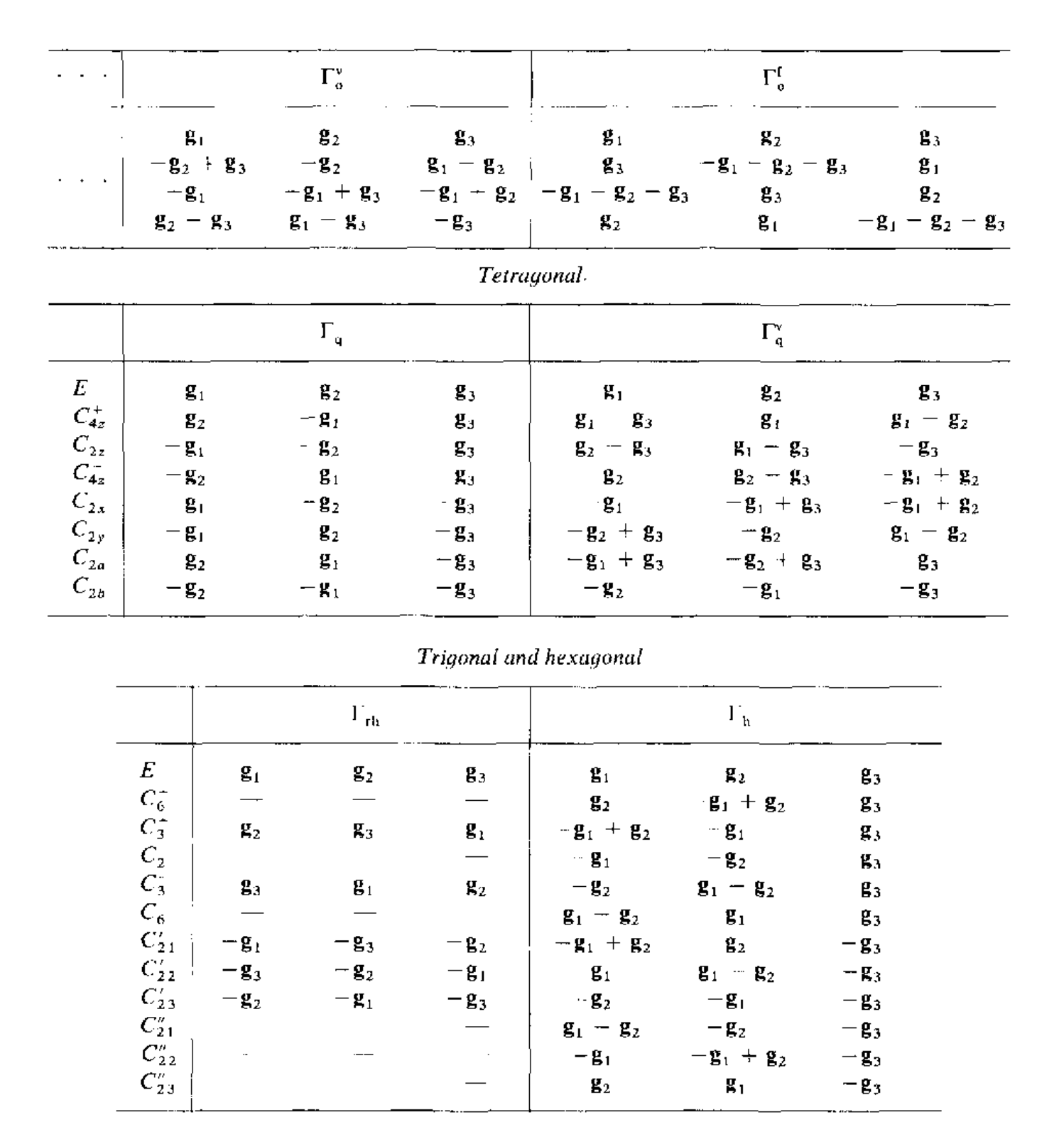
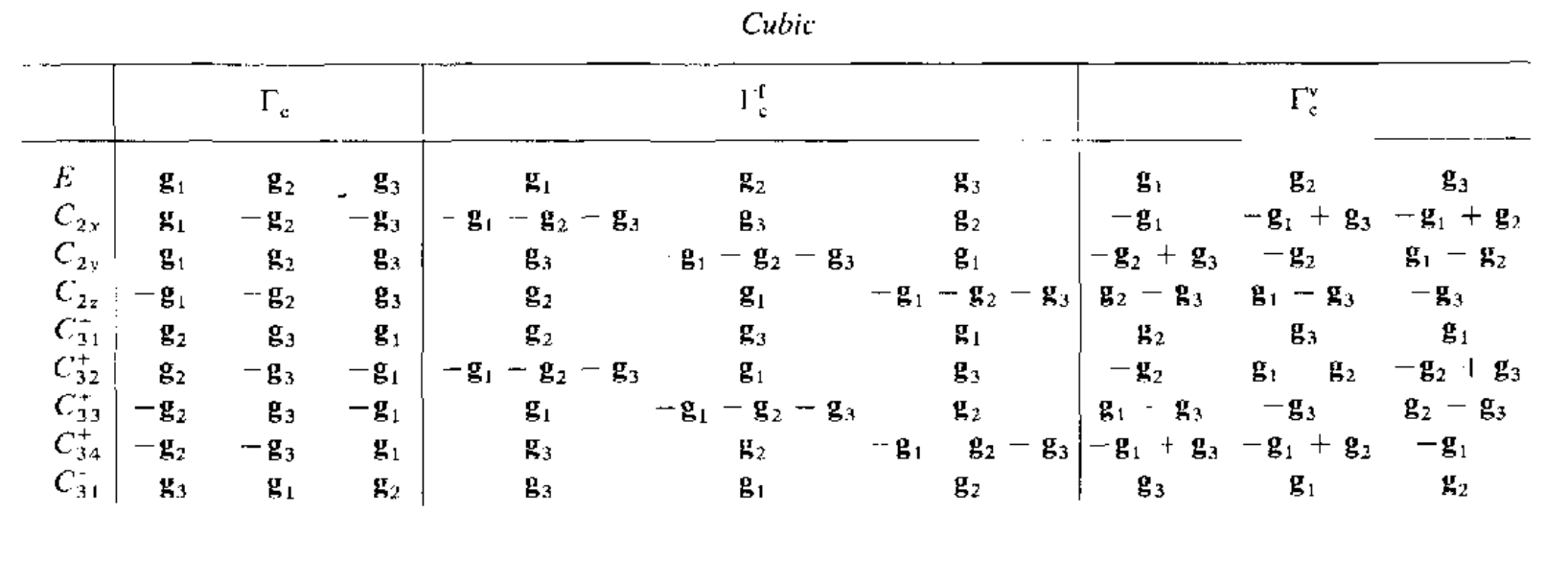
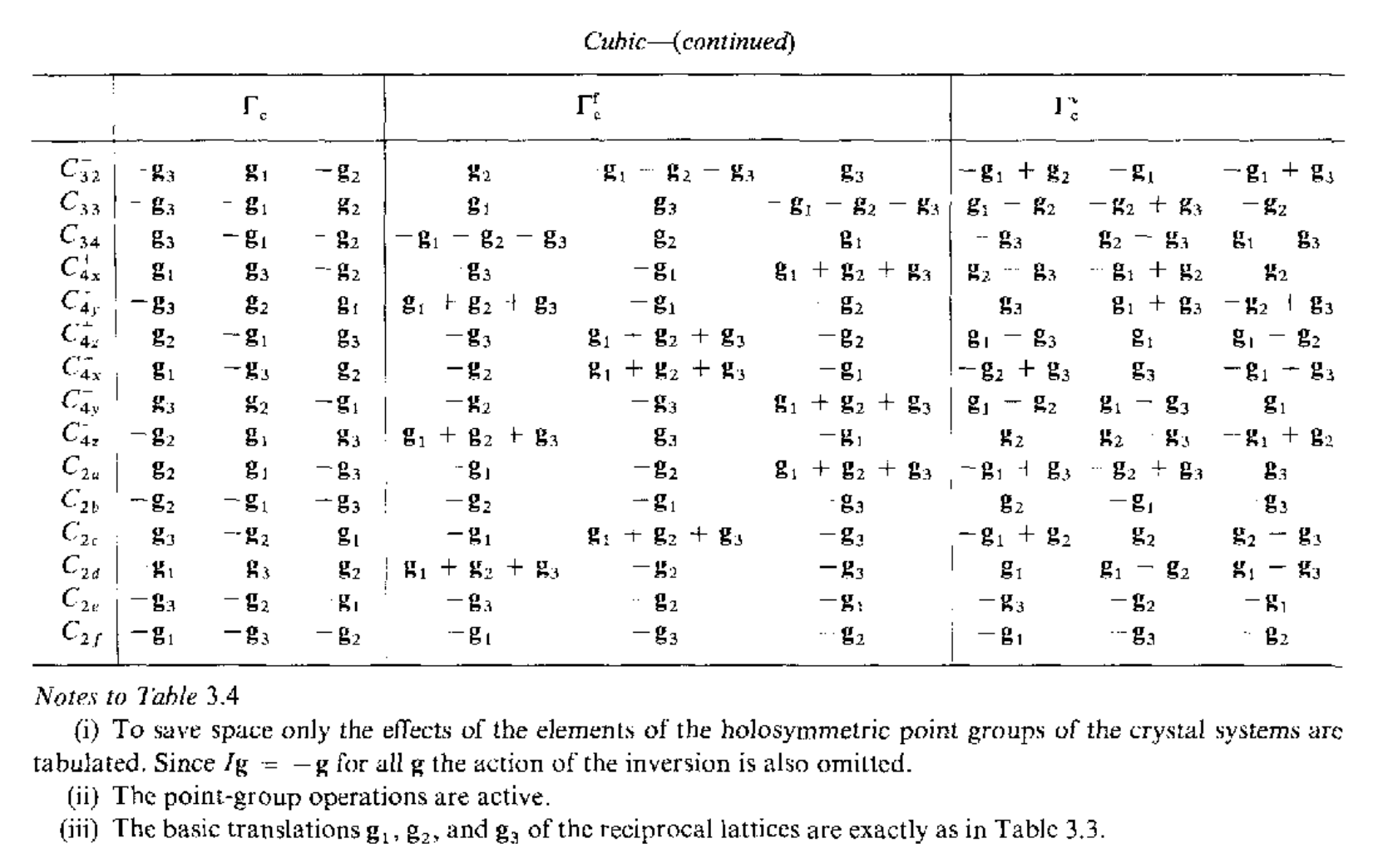
利用SpaceGroupIrep来得到
The classification of points and lines of symmetry
三维空间中红一共有14种不同的布拉菲点阵,但是有的点阵只有一种布里渊区,有的点阵可以有几种不同形式的布里渊区,讲这些所有的布里渊区集合到一起,总共有22中布里渊区,如下所示
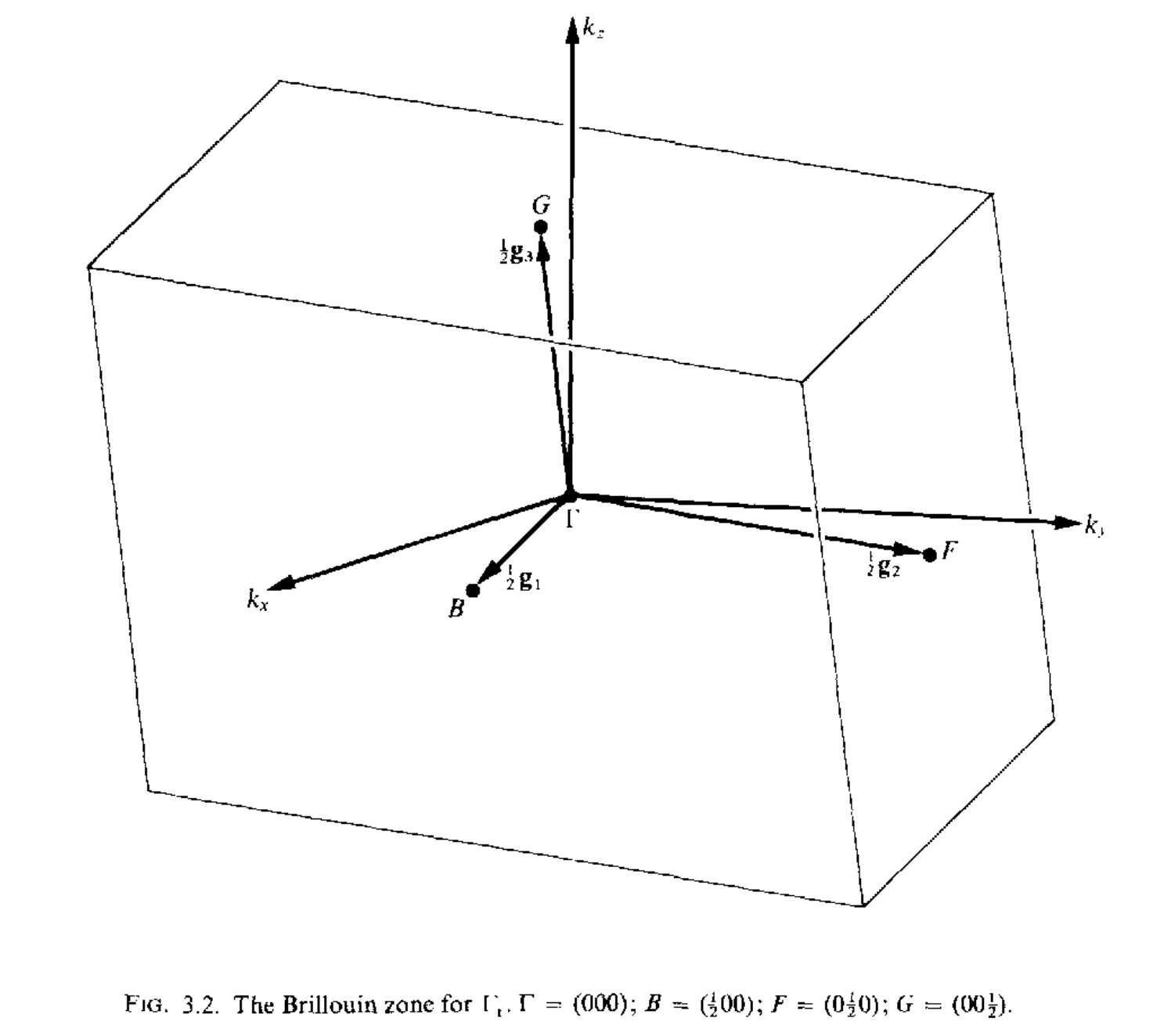
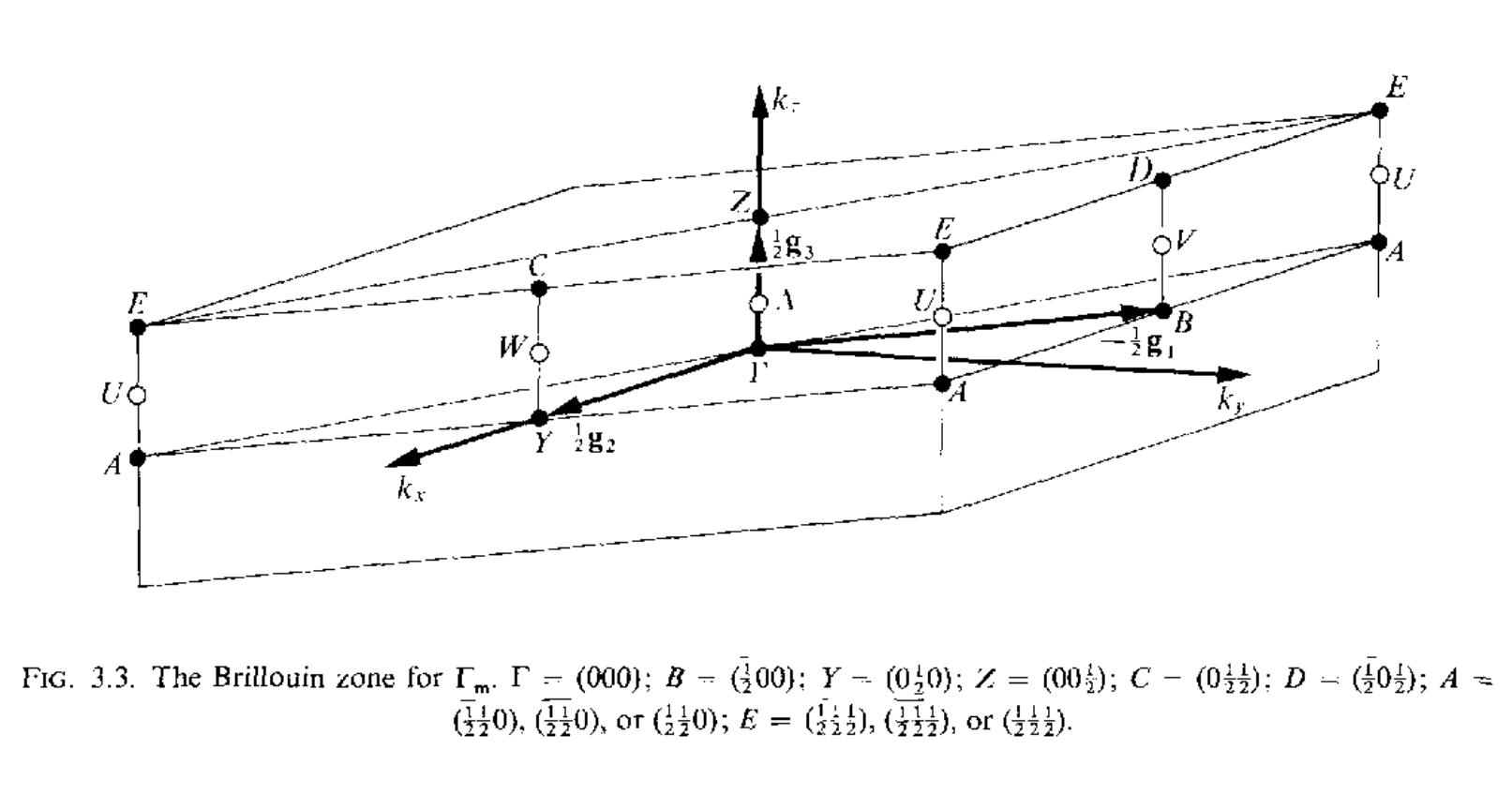

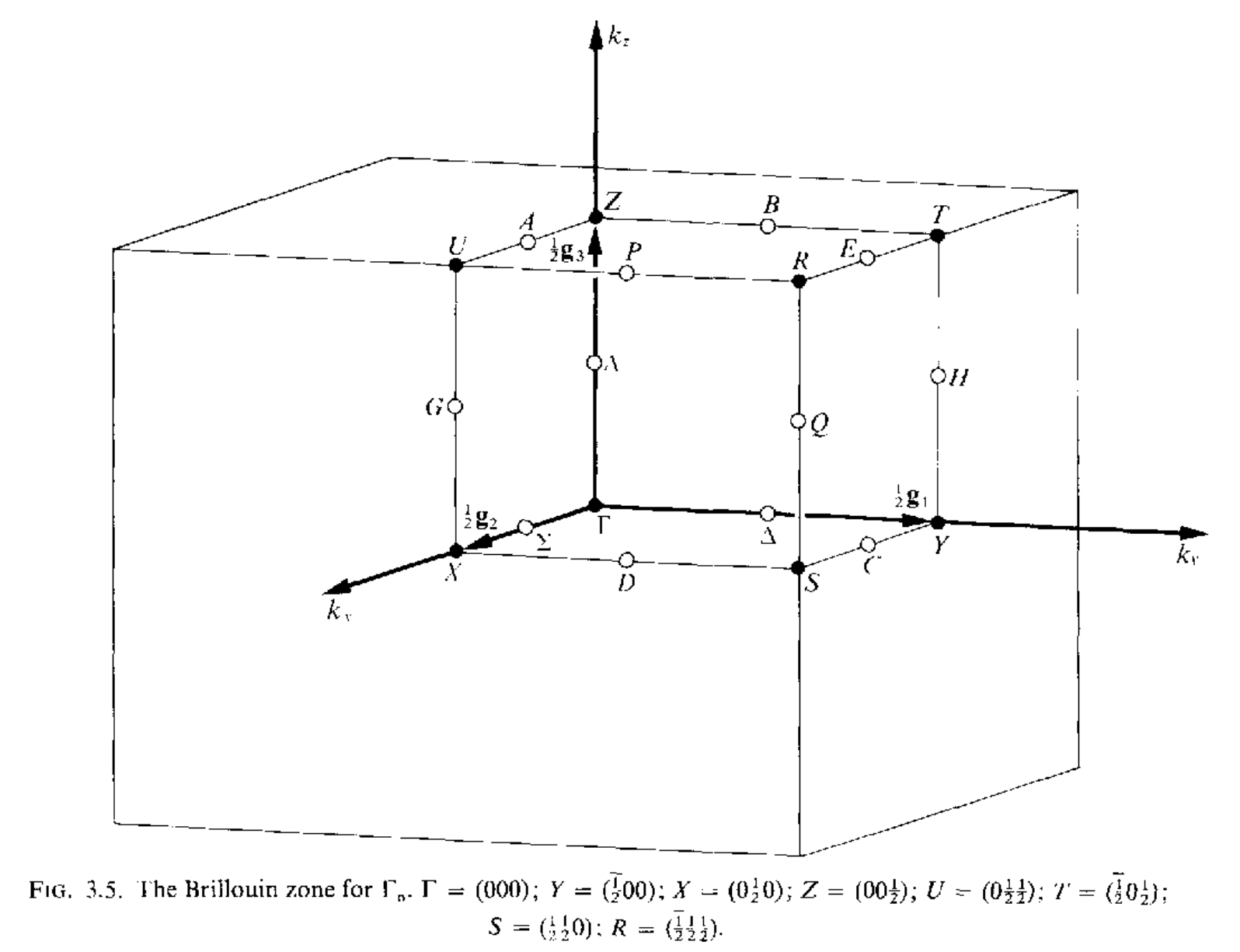
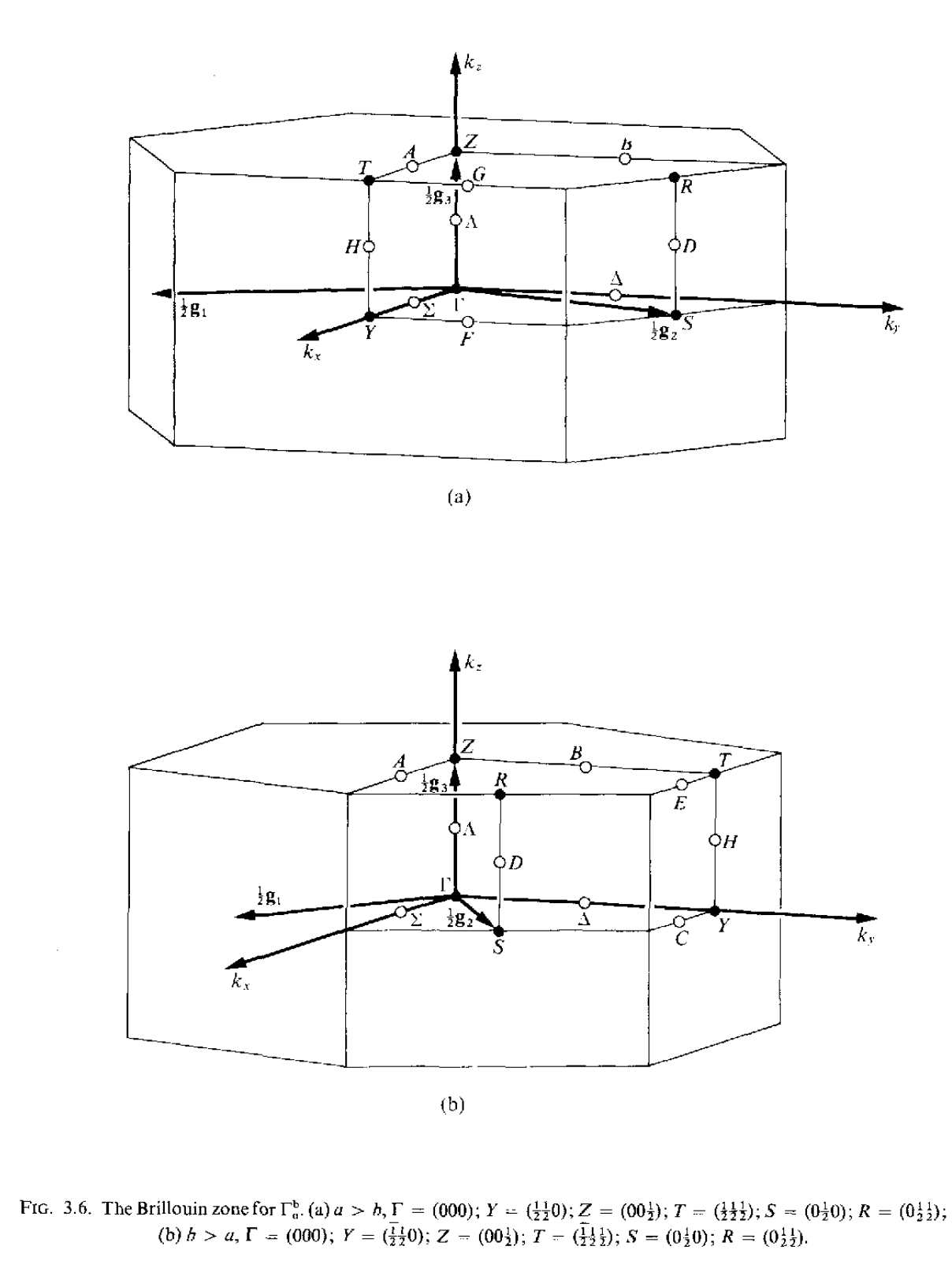
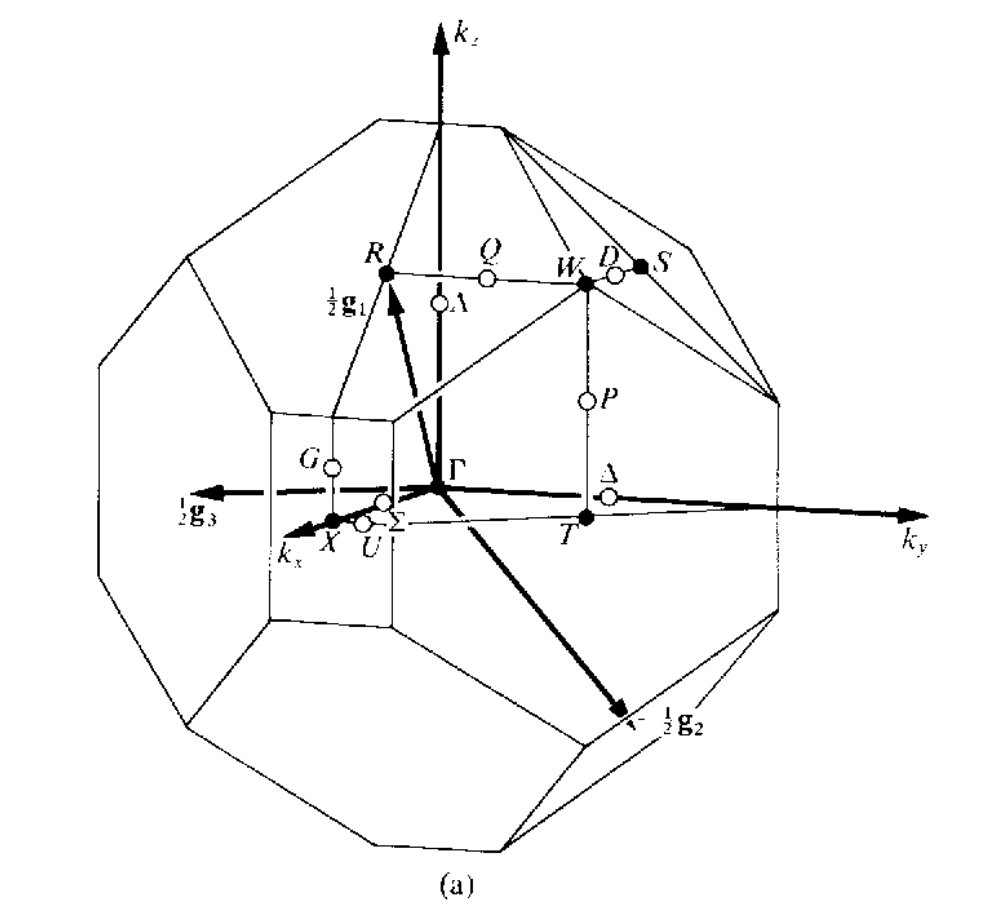
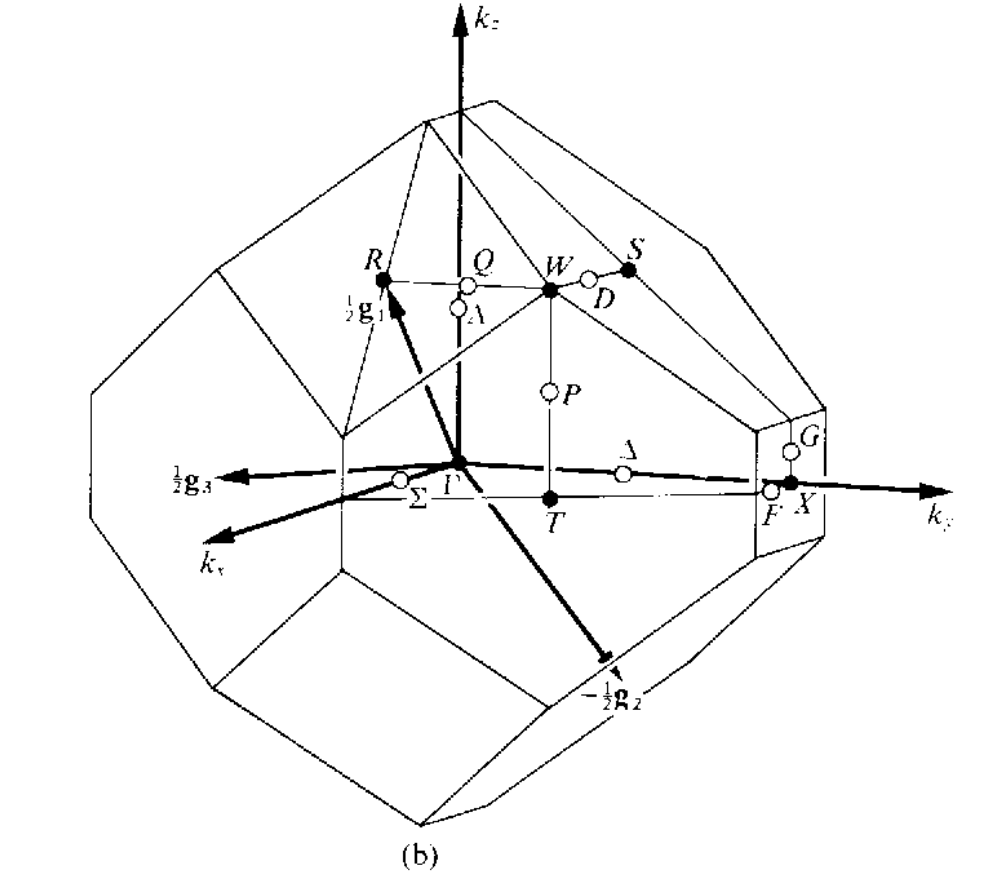
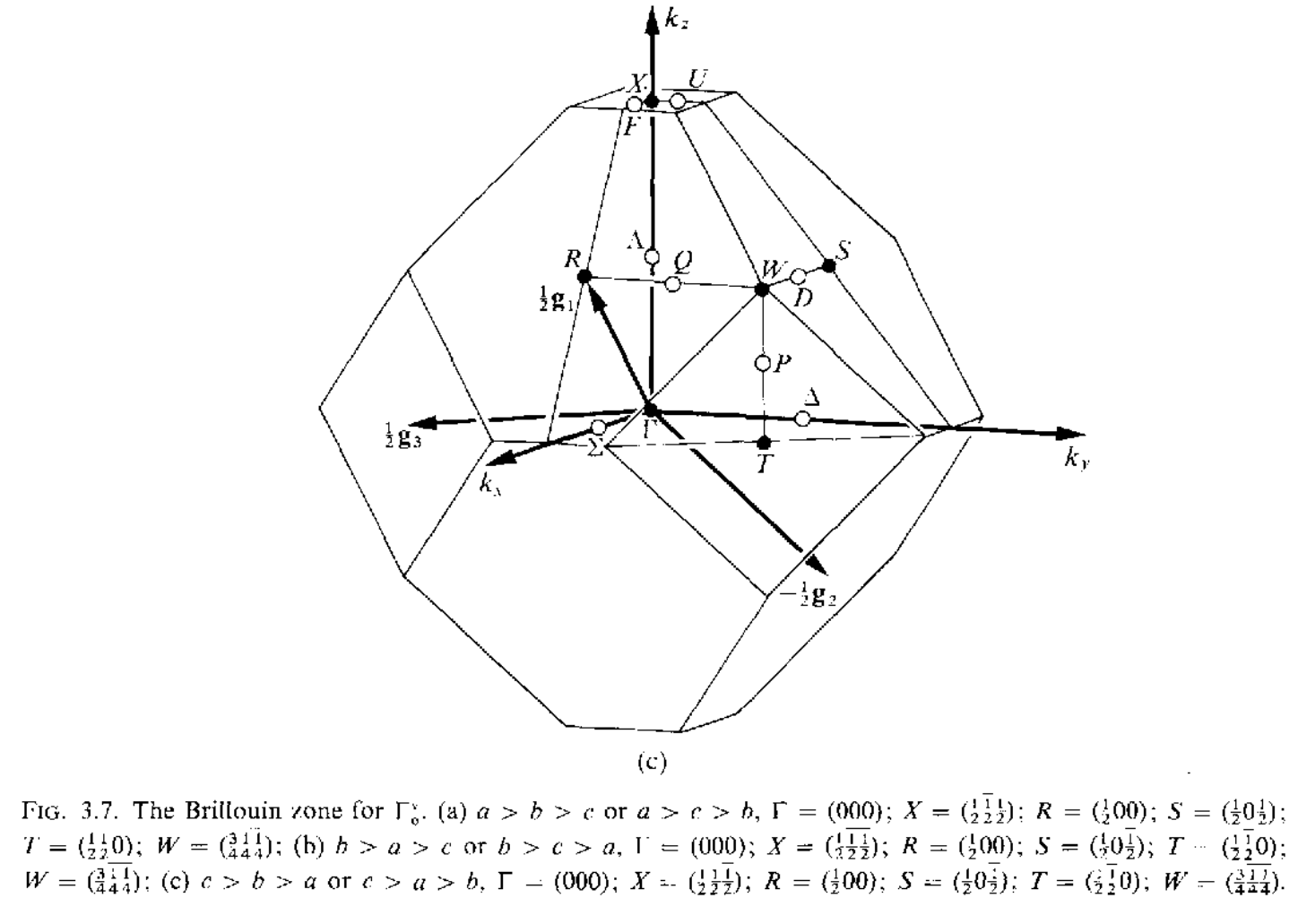
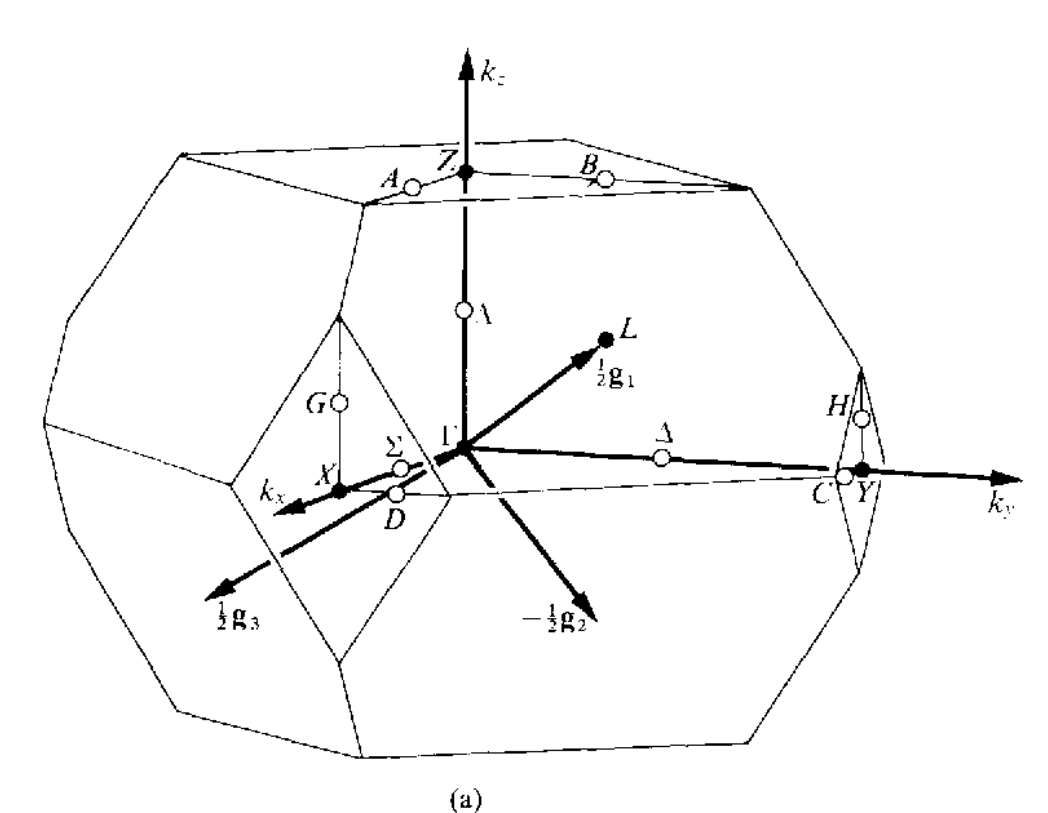
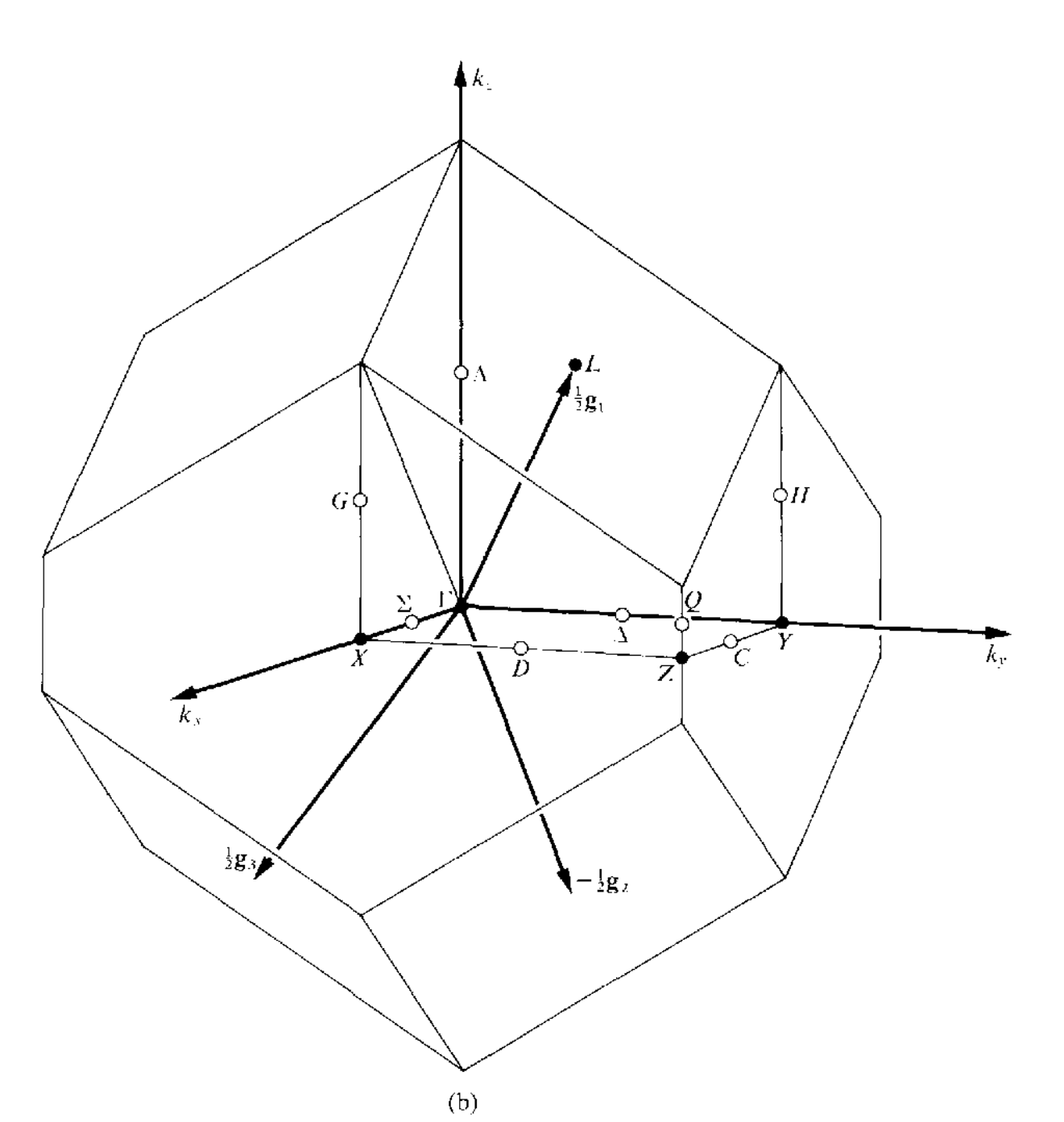
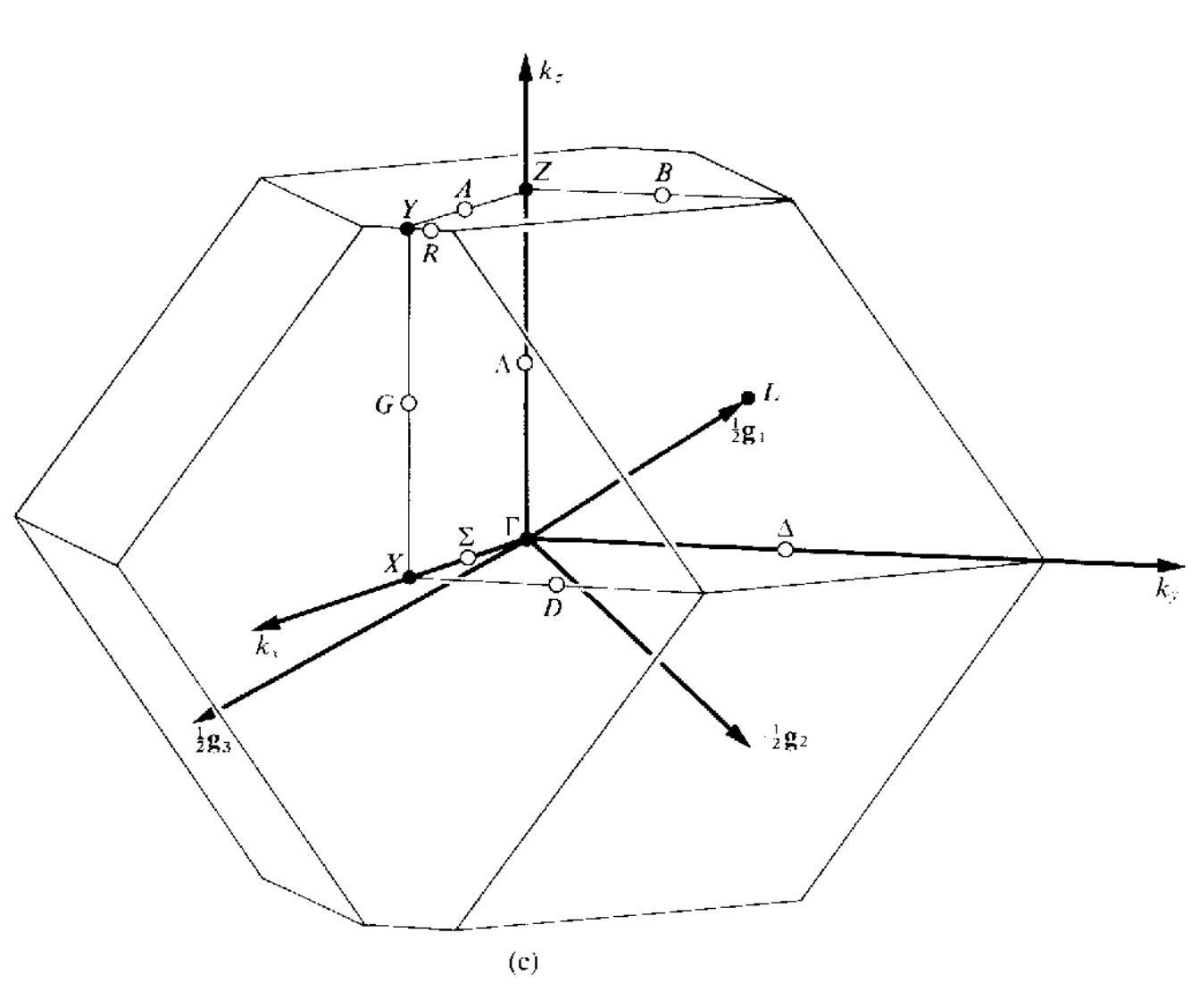
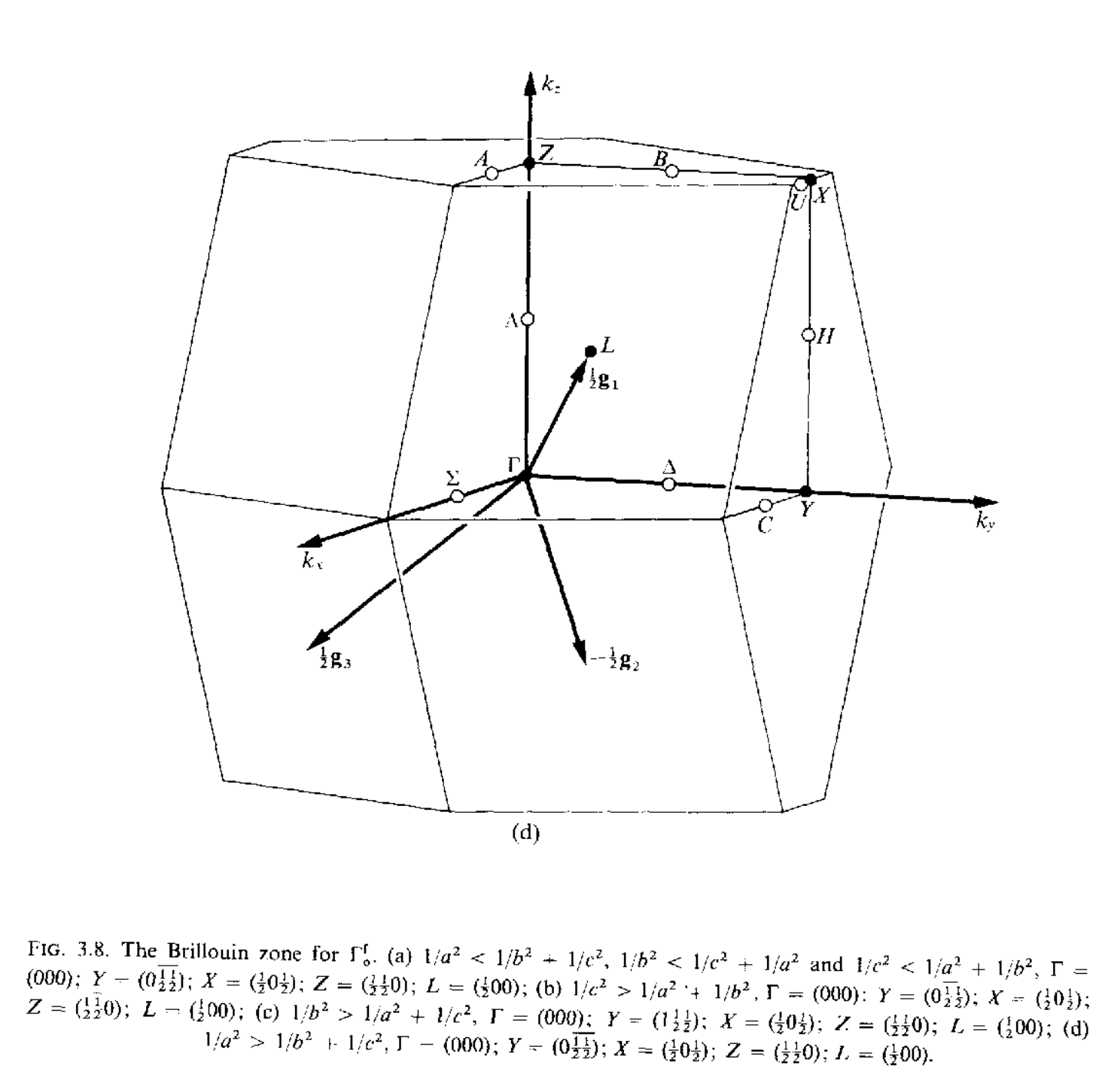
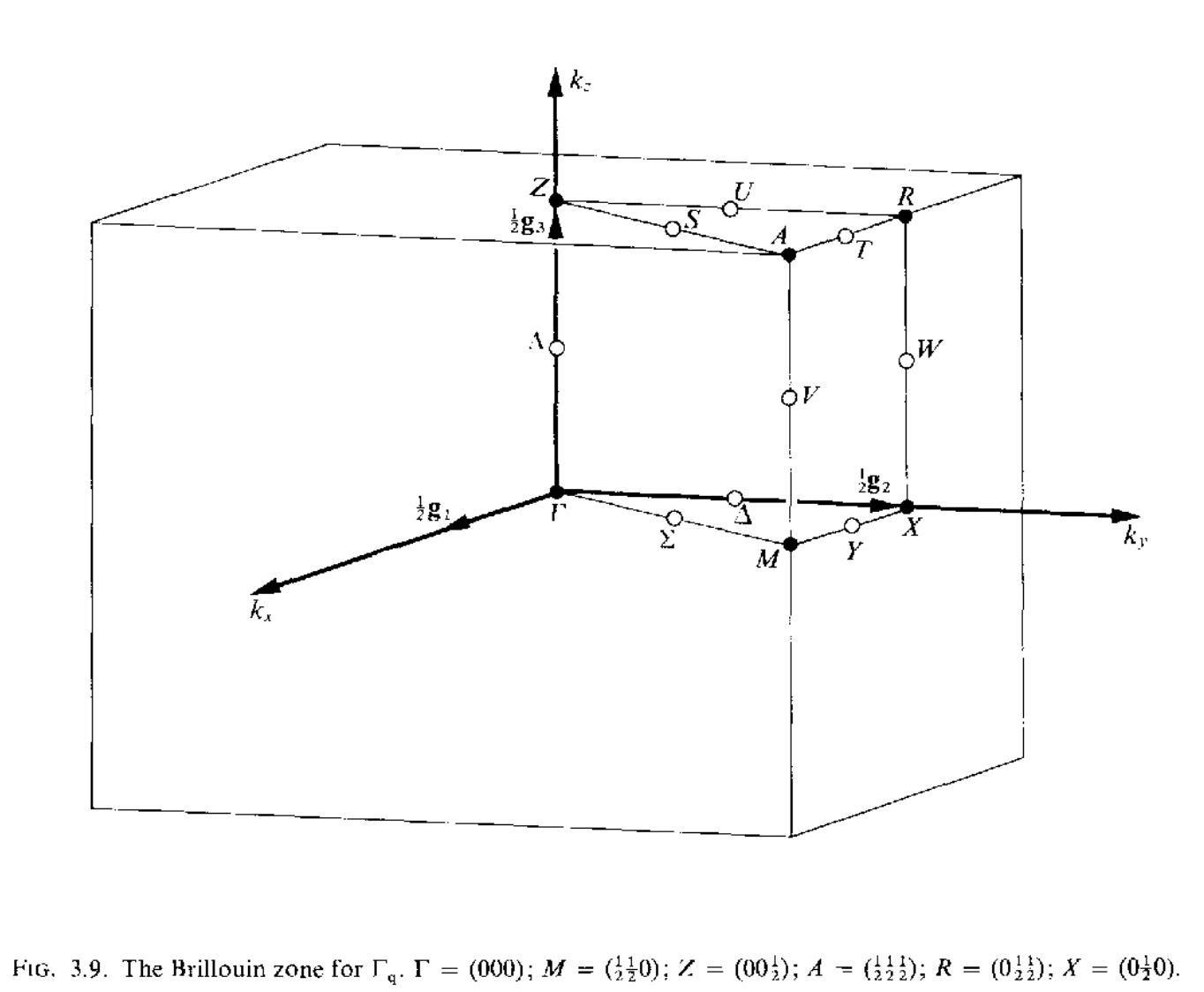
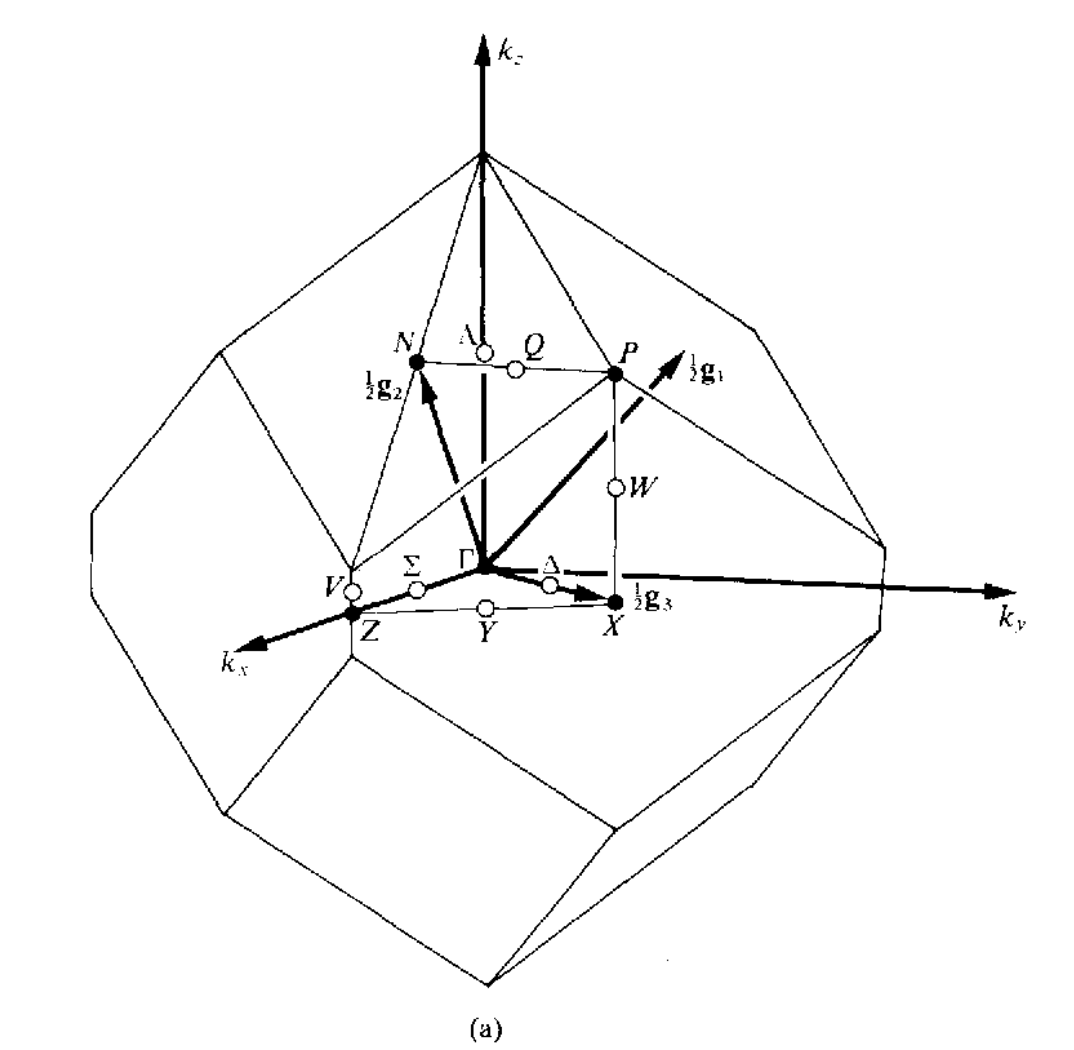
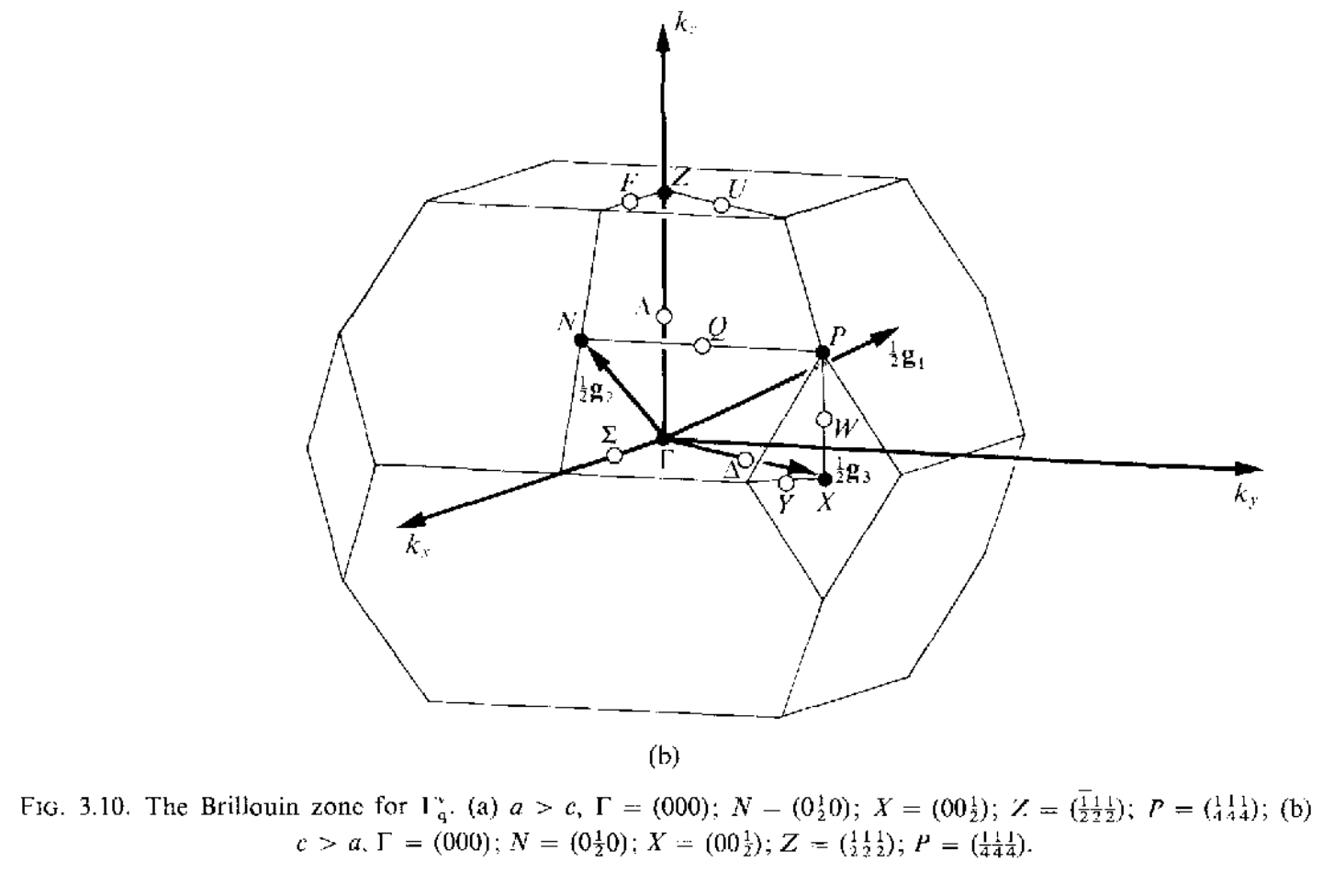
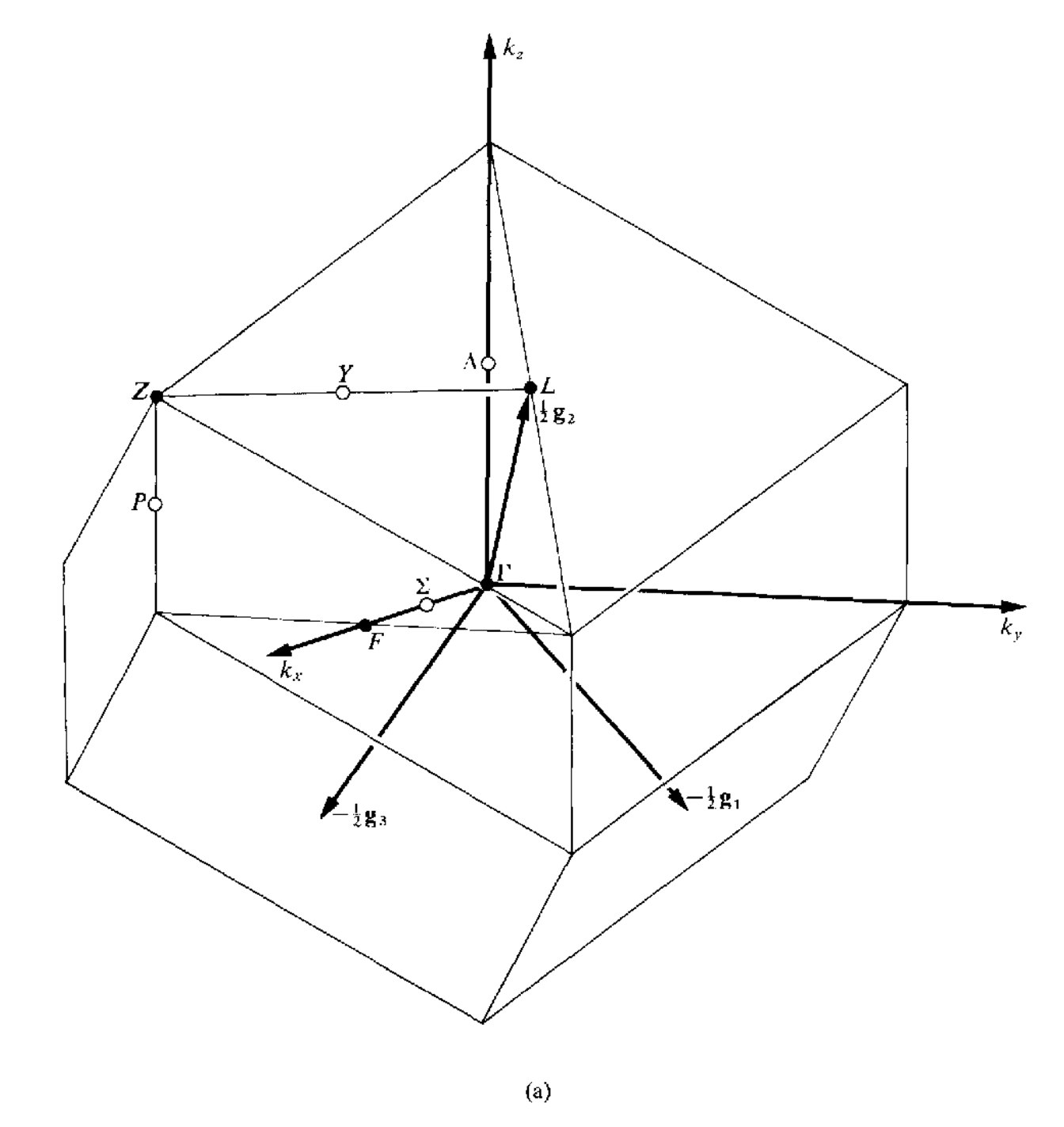
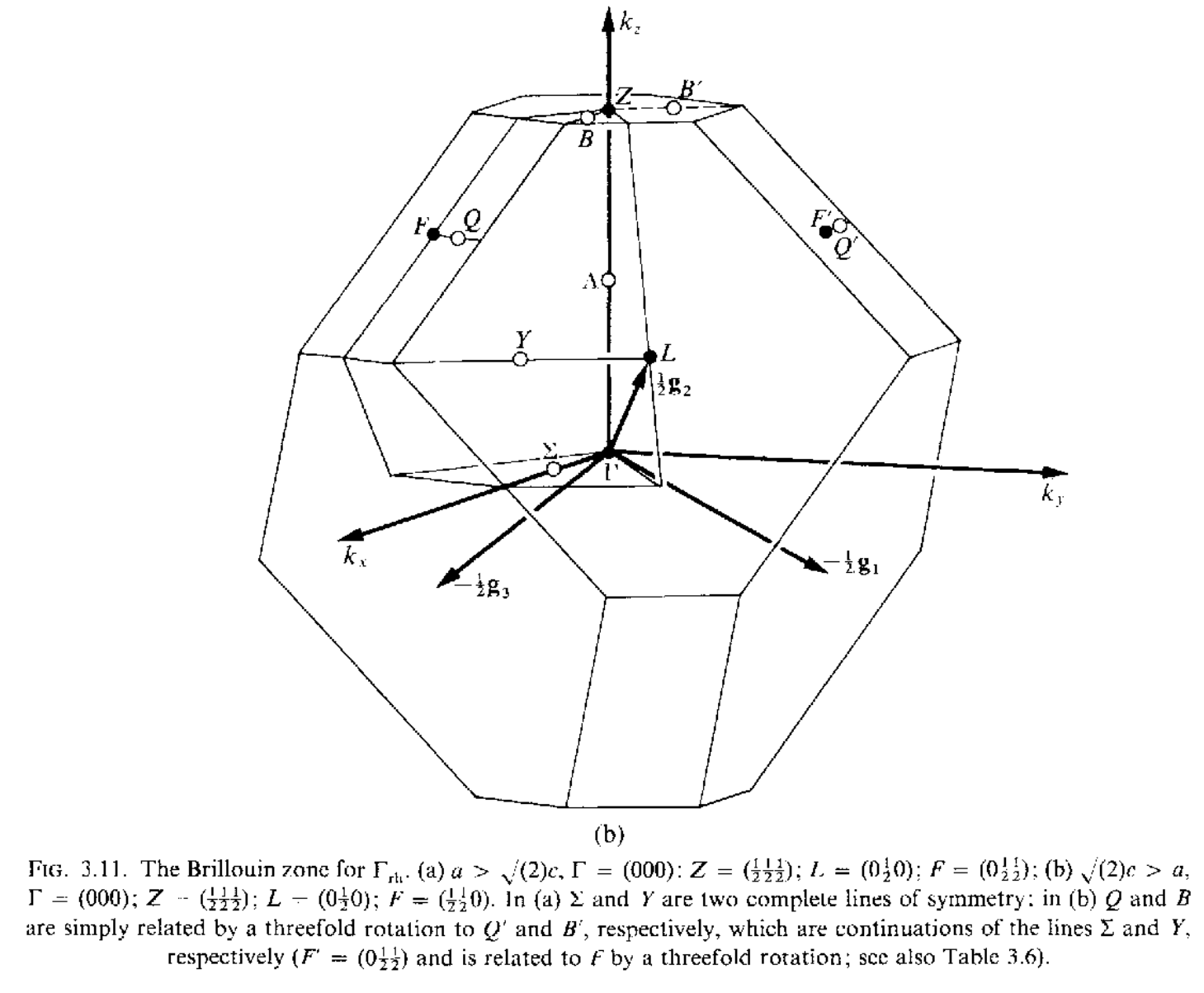
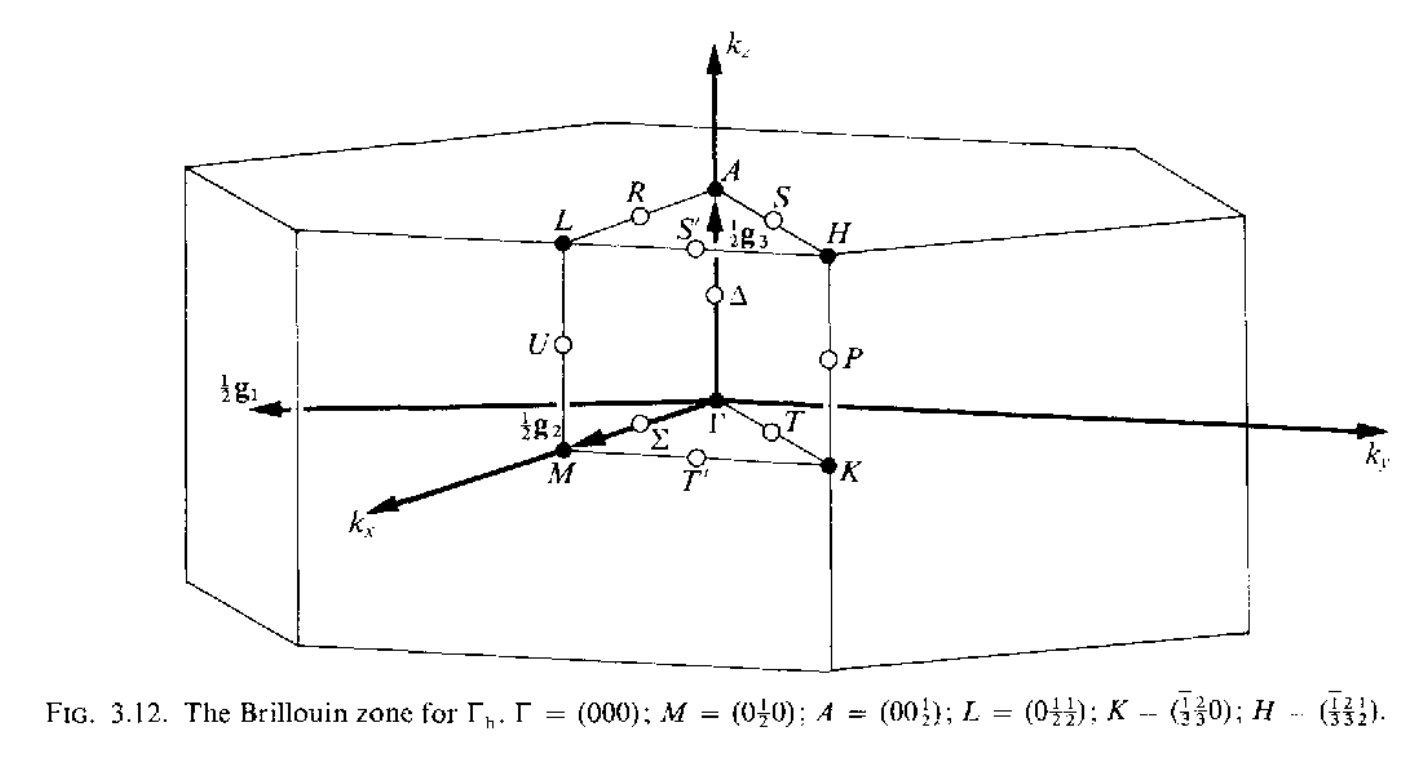
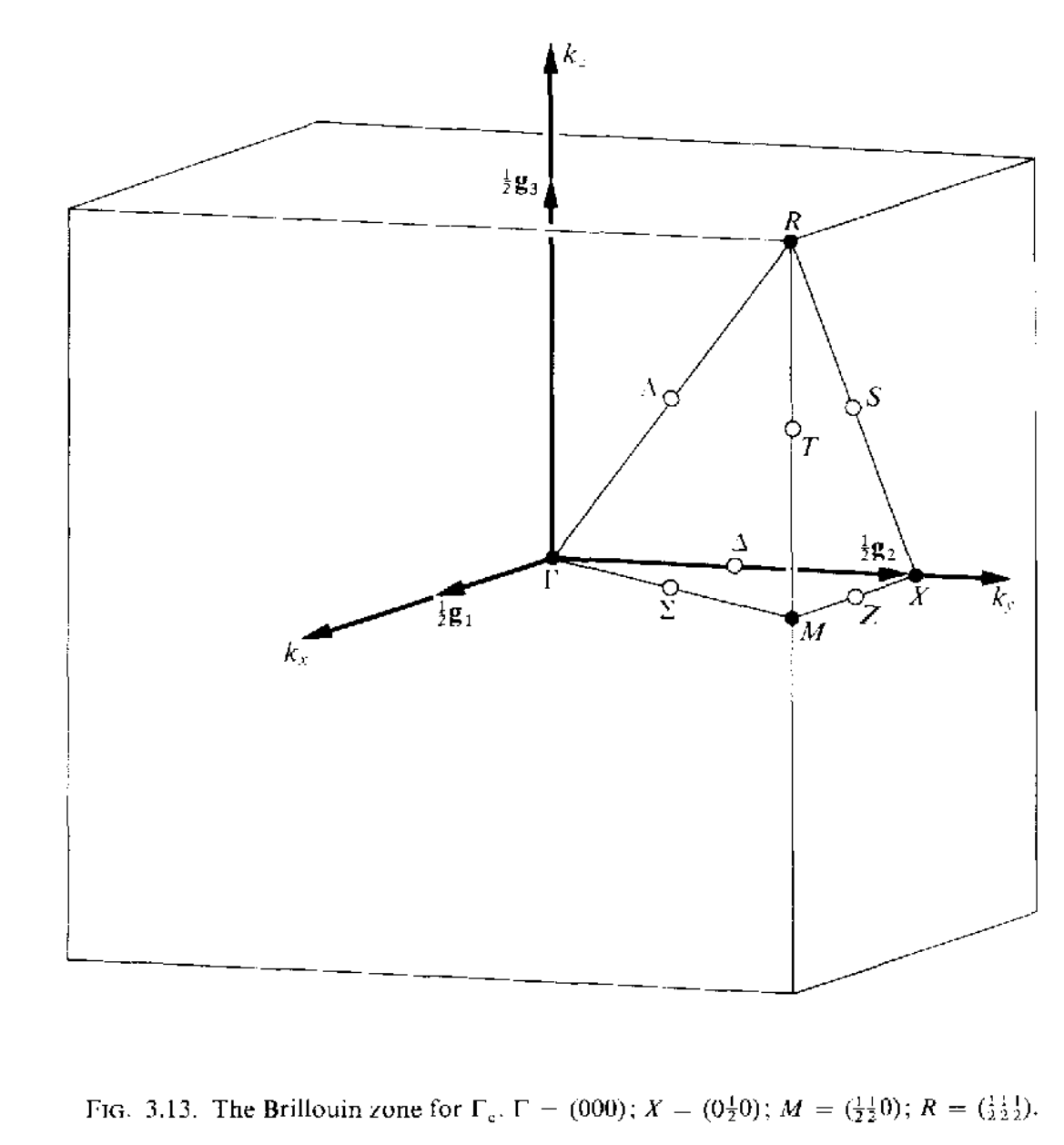
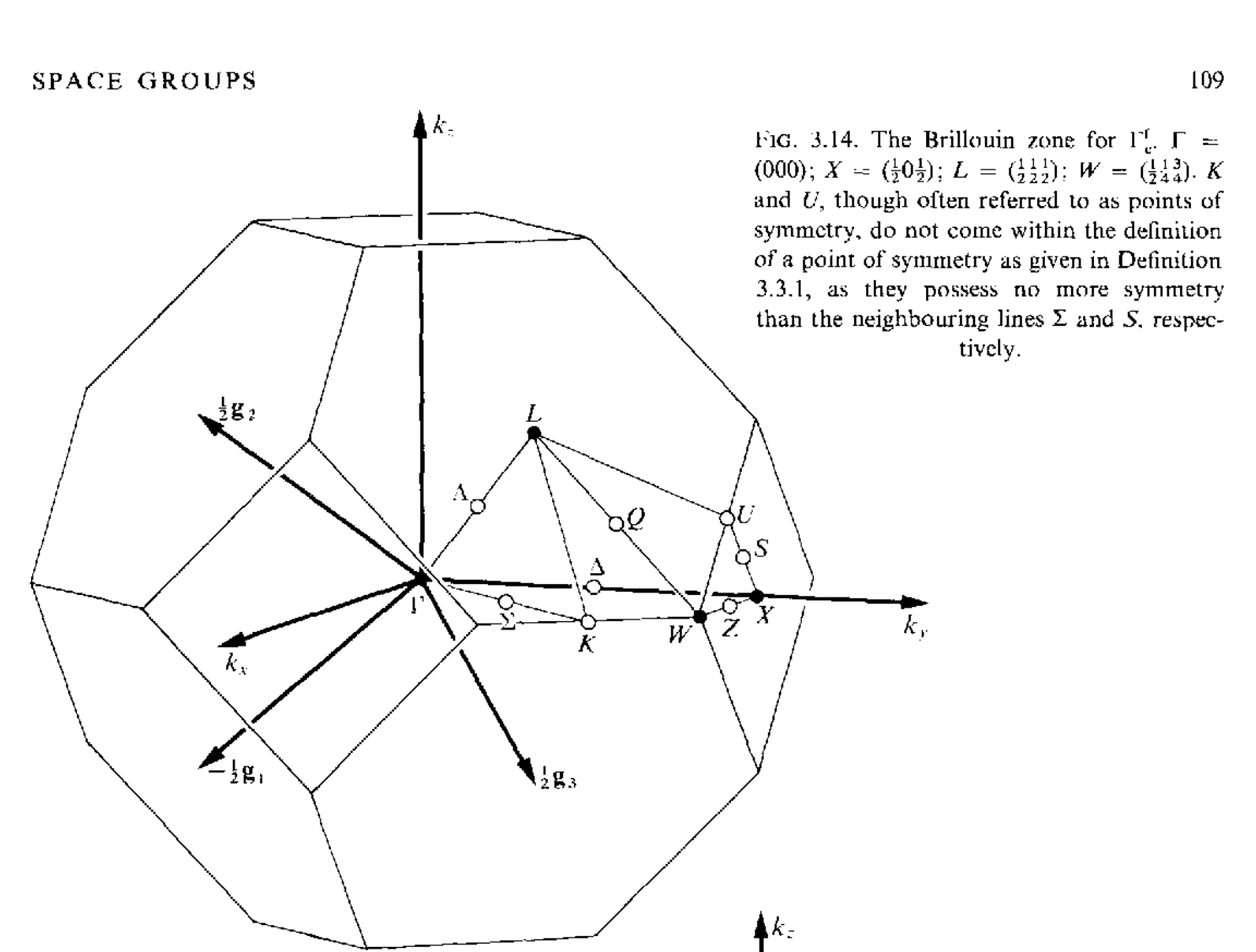
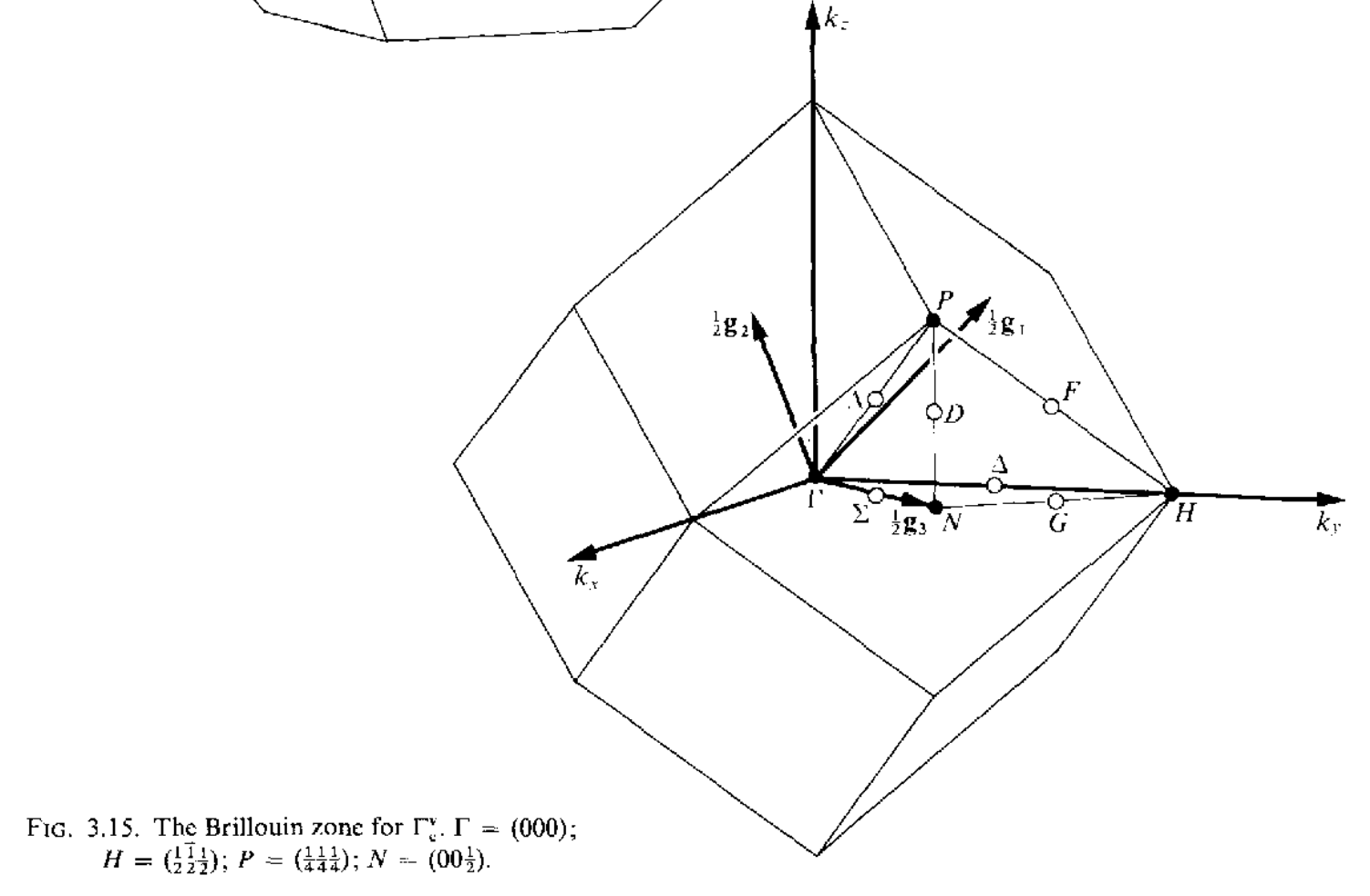

当任意两个矢量$\mathbf{k}_1,\mathbf{k}_2$之间的差$\mathbf{k}_1-\mathbf{k}_2=a_1\mathbf{g}_1+a_2\mathbf{g}_2+a_3\mathbf{g}_3(a_1,a_2,a_3\in\mathcal{Z})$的时候,这两个矢量是等价的,在布里渊区内,不存在等价的波矢,但是在布里渊区的表面上,可能存在着等价的两个波矢.
假定$\mathbf{P}$是晶体系统的全对称点群,对布里渊区中的一个波矢$\mathbf{k},\mathbf{P}$中的对称操作可以将其变换到$\mathbf{k}$本身或者其等价位置,这些对称操作就可以构成$\mathbf{P}$的一个子群$\mathbf{P}(\mathbf{k})$,被称为$\mathbf{k}$的对称群.
对称点:在波矢$\mathbf{k}$附近存在$N$个相邻的波矢,在这些波矢中,如果只有波矢$\mathbf{k}$具有对称群$\mathbf{P}(\mathbf{k})$,那么称$\mathbf{k}$是个对称点.
上面的定义也就是说,如果$\mathbf{k}^{‘}\neq\mathbf{k}$,那么$\mathbf{P}(\mathbf{k}^{‘})$是$\mathbf{P}(\mathbf{k})$的正规子群,也就是说在这些波矢中,$\mathbf{k}$处的对称性是最高的.
对称线:在波矢$\mathbf{k}$附近的$N$个波矢中,总存在穿过$\mathbf{k}$的一条线,这条线上的所有的点都具有和$\mathbf{k}$相同的对称群,那么就将$\mathbf{k}$称为对称线(面).
一般点:如果波矢$\mathbf{k}$附近的所有点都具有相同的对称群,那么$\mathbf{k}$被称为一般点.
对于一般点上的对称群,其中只包含单位元操作;对于对称面群$\mathbf{P}(\mathbf{k})$通常只包含单位元和反射操作这两个元素.
对于每一个布里渊区,存在一个基本区域$\Omega$,其中$\sum_RR\Omega$就是整个布里渊区的体积,这里$R$是对应晶体系统的全对称群$\mathbf{P}$.
\[\Omega=\frac{8\pi^3}{V\rvert\mathbf{P}\rvert}\]这里的$\rvert\mathbf{P}\rvert$是全对称群$\mathbf{P}$的阶数.这里的$\Omega$可以认为是布里渊区的最小单元,其余的部分可以通过晶体满足的对称性,通过对称操作得到,所以在计算的时候,也只需要计算这个最小区域内的性质即可.
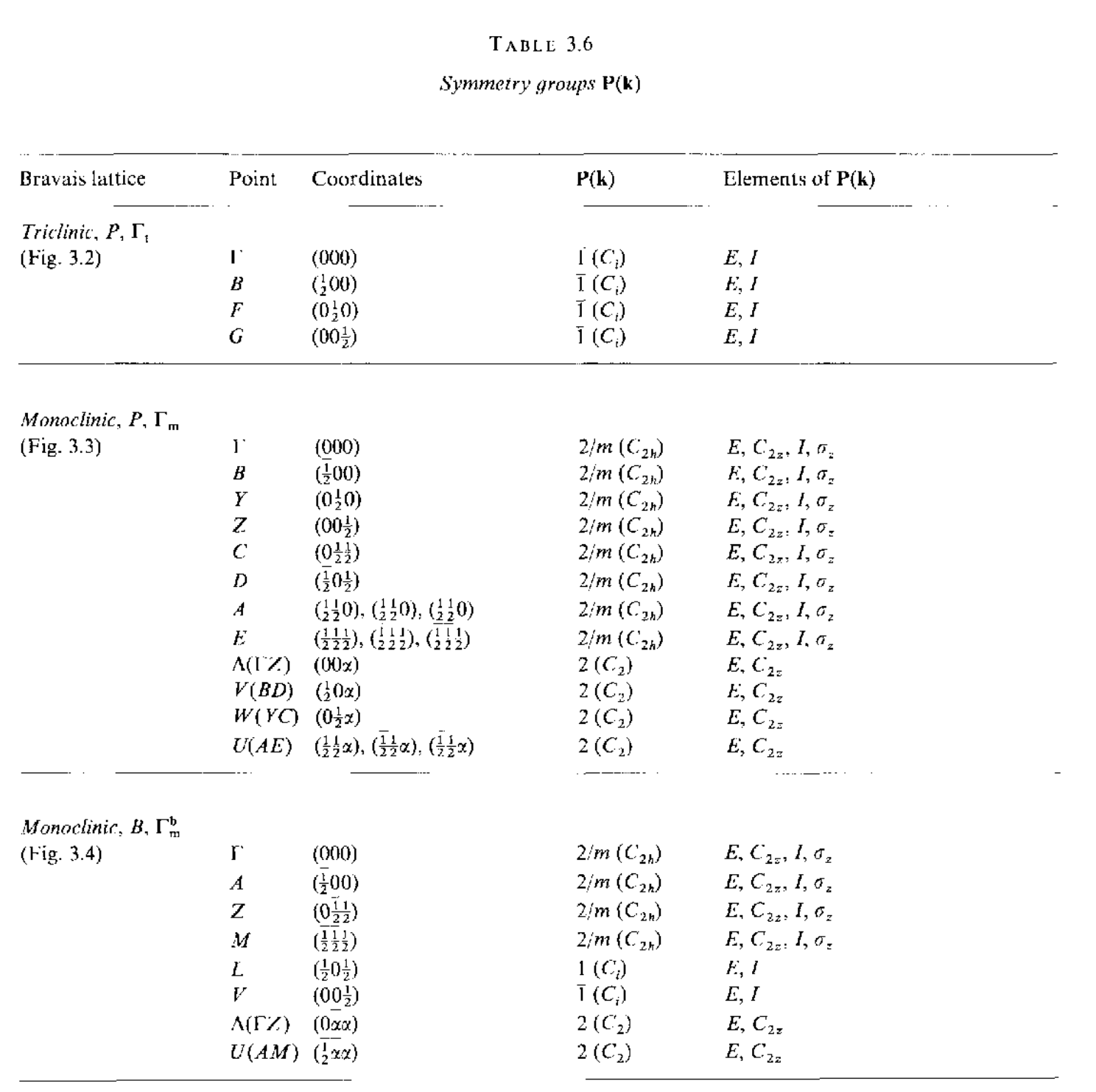
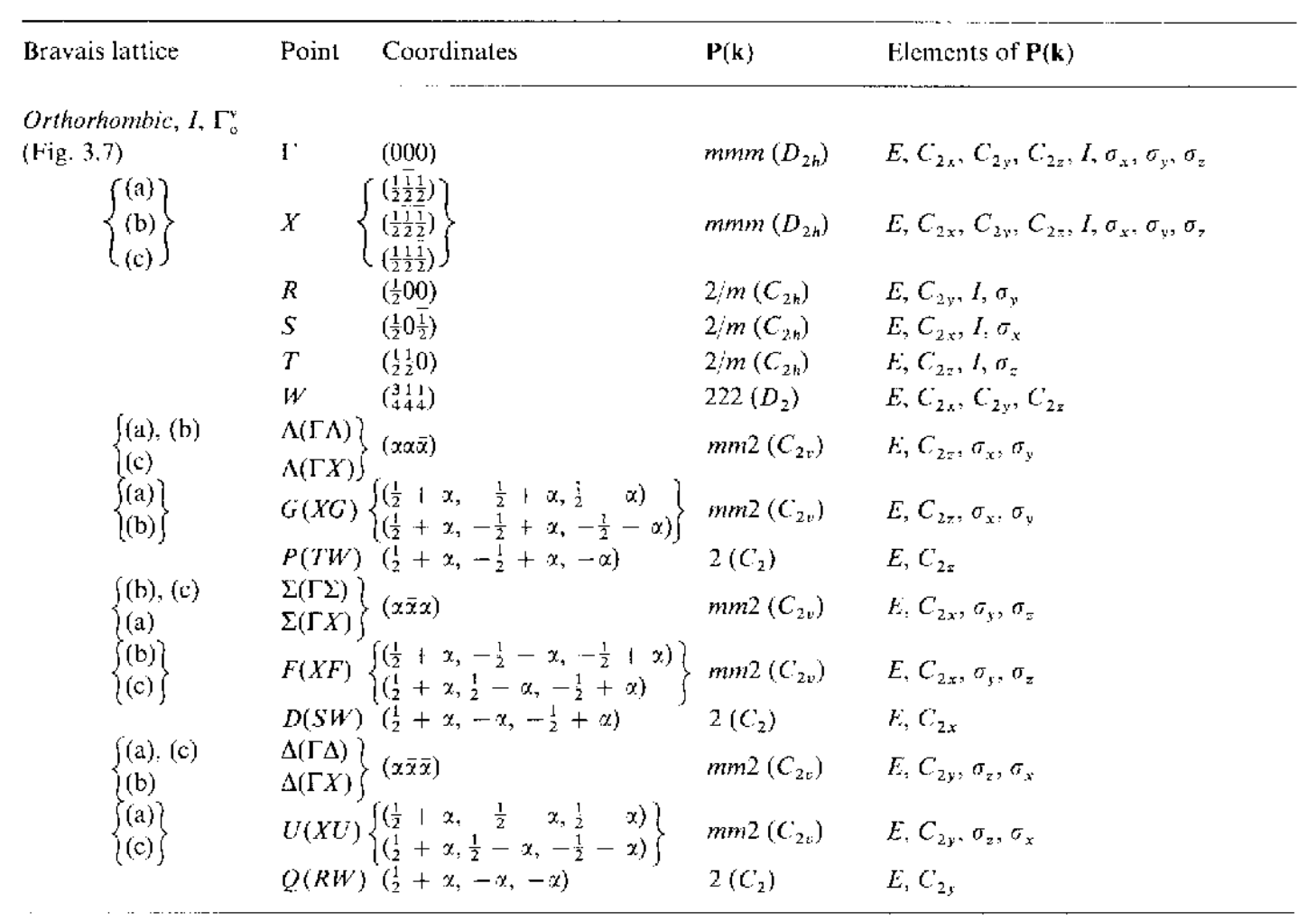
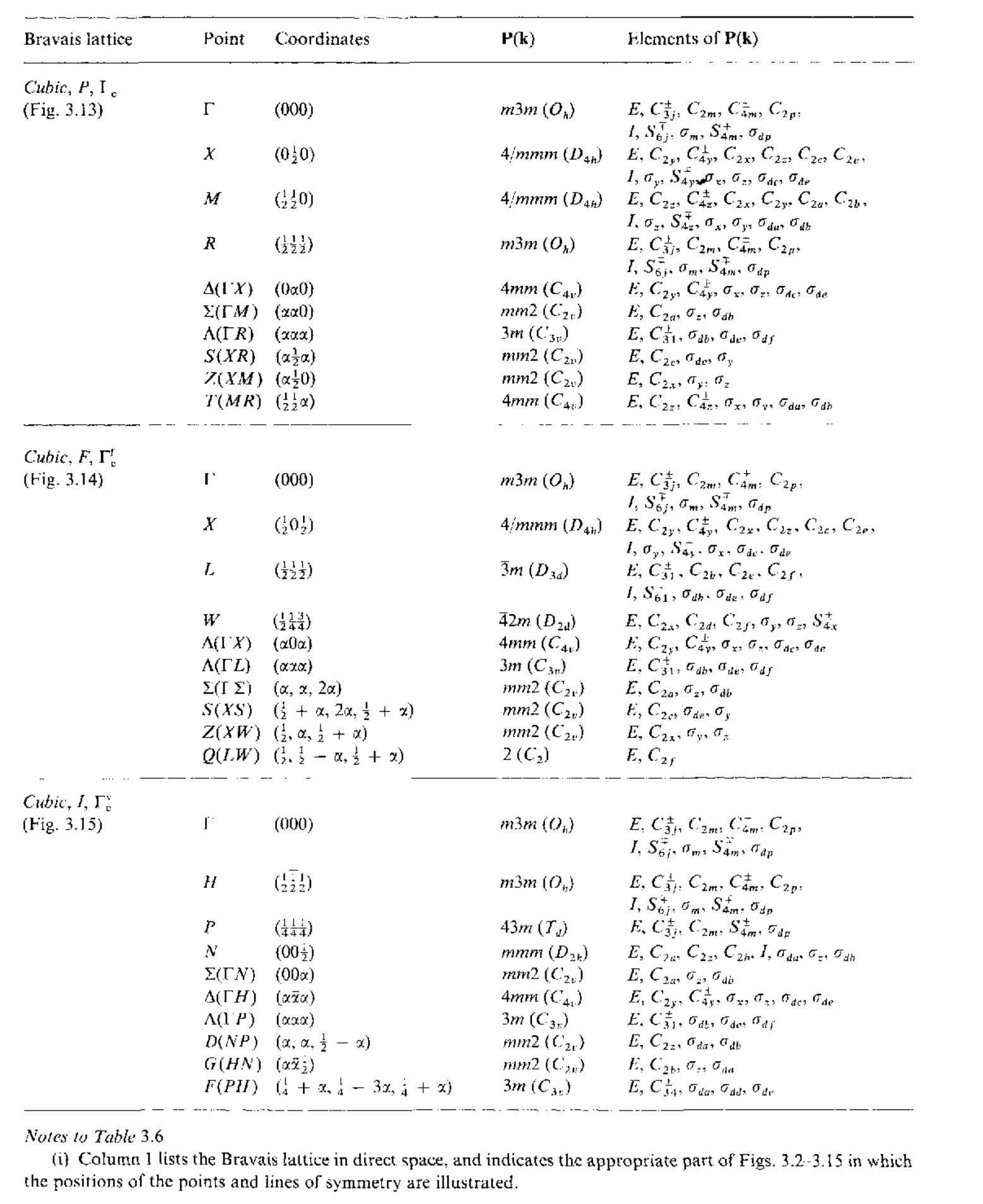
在上面22中不同的布里渊区中,有一些布里渊区是属于同一个布拉菲点阵的,虽然这两个布里渊区明显结构不同,但是每个里面的对称点数目都是相同的.这些布里渊区中都存在着高对称点和高对称线,它们都满足一定的对称操作,即每个对称点$\mathbf{k}$都存在一个对称群$\mathbf{P}(\mathbf{k})$,下面罗列出所有高对称点的对称群




公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |