学习群论有一段时间了, 这里想结合一些工具, 并通过一些书籍阅读来将自己所学到的内容整理一下, 同时加深一下自己对这些知识内容的理解.
平移群不可约表示
每个空间群都有一个不变子群$\mathbf{T}$,它包含了基于这个空间群的布拉菲点阵上的所有平移操作${E\rvert n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3}$,在采用周期性边界条件之后$0\le n_i<N_i,i=1,2,3$.平移操作满足${E\rvert\mathbf{t}}{E\rvert\mathbf{s}}={E\rvert\mathbf{t+s}}$,因为采用了周期性边界条件,空间群对应的平移操作可以表示为三个阶数为$N_i$的循环群的外直积$\mathbf{T}=\mathbf{T}_1\otimes\mathbf{T}_2\otimes\mathbf{T}_3$,而对于一个循环群而言,它的表示是比较容易求解得到的.
这里平移群表示为三个方向上的平移群的外直积,可以理解为这三个方向上的平移是互不影响的,也就是说无论平移的顺序如何,单独方向上的平移操作总是不会受到其他两个方向上操作的影响.
对于平移群$\mathbf{T}_1$的不可约表示$\Delta$是$N_1$个数,可以通过$p_1(0\leq p_1\leq N_1)$来标记
\[\Delta^{p_1}(\{E\rvert n_1\mathbf{t}_1\})=\exp(-2\pi in_1p_1/N_1)\]通过直积表示,就可以轻易的得到平移群$\mathbf{T}$的不可约表示,它们都是1维的,而且是$N_1N_2N_3$个数,标记$k_i=p_i/N_i$并选择$\mathbf{k}=(k_1,k_2,k_3)$作为倒空间中的矢量
\[\mathbf{k}=k_1\mathbf{g}_1+k_2\mathbf{g}_2+k_3\mathbf{g}_3\label{eq1}\]则对应的$\mathbf{T}$的不可约表示为
\[\Delta^\mathbf{k}[\{E\rvert n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3\}]=\exp[-i\mathbf{k}\cdot(n_1\mathbf{t}_1+n_2\mathbf{t}_2+n_3\mathbf{t}_3)]\]如果两个矢量之间是等价的或者相差一个倒格矢$\mathbf{k}^{‘}=\mathbf{k}+\mathbf{g}$,由于$\exp(i\mathbf{g}\cdot\mathbf{t})=1$,可以得到
\[\Delta^{\mathbf{k}^{'}}(\mathbf{t})=\exp[-i(\mathbf{k+g}\cdot\mathbf{t})]=\Delta^\mathbf{k}(\mathbf{t})\]所以可以取值的$\mathbf{k}$值共有$N_1N_2N_3$个,它们总是分布在布里渊区内,因此平移群$\mathbf{T}$的所有不可约表示就是定义在布里渊区上的一系列$\mathbf{k}$点.在倒空间体积为$8\pi^3/V$的时候,共有$N_1N_2N_3$个$\mathbf{k}$点分布在其中,那么密度$n(\mathbf{k})$就是$N_1N_2N_3V/8\pi^3=W/8\pi^3$,这里的$W$是实空间中晶体的体积,$V$是晶体元胞的体积.
\[n(\mathbf{k})=\frac{W}{8\pi^3}\]对于表示$\Delta^\mathbf{k}$的基函数可以选择平面波$\exp(i\mathbf{k}\cdot\mathbf{r})$
\[\begin{equation}\{E\rvert\mathbf{t}\}\exp(i\mathbf{k}\cdot\mathbf{r})=\exp(i\mathbf{k}\cdot\mathbf{r-t})=\exp(-i\mathbf{k}\cdot\mathbf{t})\exp(i\mathbf{k}\cdot\mathbf{r})=\Delta^\mathbf{k}\{E\rvert\mathbf{t}\}\exp(i\mathbf{k}\cdot\mathbf{r})\end{equation}\]除了利用平面波之外,可以选择具有下列形式的函数
\[\Psi_\mathbf{k}(\mathbf{r})=\exp(i\mathbf{k}\cdot\mathbf{r})u_\mathbf{k}(\mathbf{r}),\quad u_\mathbf{k}(\mathbf{r})=u_\mathbf{k}(\mathbf{r+t})\text{ for all }\mathbf{t}\]Bloch定理:在周期势场$V$中运动的粒子或者准粒子,其波函数具有$\mathbf{T}$定义的周期性,可以被写作$\Psi_\mathbf{k}(\mathbf{r})=\exp(i\mathbf{k}\cdot\mathbf{r})u_\mathbf{k}(\mathbf{r})$,这里$u_\mathbf{k}(\mathbf{r})$具有和$V$相同的周期性,此处$\mathbf{k}$的取值为(\ref{eq1}).
三维空间230个空间群分类
一个空间群有三维的纯平移子群$\mathbf{T}$,它定义了布拉菲点阵,其满足$\mathbf{T}$的所有操作,但是布拉菲点阵同样在点群$\mathbf{P}$的操作下也满足对称性.如果$\mathbf{\Gamma}$是布拉菲点阵的完整对称群,那么$\mathbf{\Gamma}=\mathbf{T}\wedge\mathbf{P}$,是平移群和点群的半直积.$\mathbf{P}$决定了$\mathbf{G}$的晶体系统.$\mathbf{\Gamma}$自己是个空间群.如果$\mathbf{G}$是个点式空间群它要么与$\mathbf{\Gamma}$一致要么是$\mathbf{\Gamma}$的子群,对于73个点式空间群,此时有$\mathbf{G}=\mathbf{T}\wedge\mathbf{Q}$,这里$\mathbf{Q}$是$\mathbf{P}$的晶系中的一个点群,它决定了空间群$\mathbf{G}$的晶体的点群.
对于剩下的153个非点式空间群,将$\mathbf{Q}$中的某些元素替换成螺旋轴操作或者滑移反射,此时的$\mathbf{Q}$不再构成一个群,因此空间群也不能写作$\mathbf{\Gamma}=\mathbf{T}\wedge\mathbf{Q}$.
如果${R\rvert\mathbf{v}}$是$\mathbf{G}$中的元素,那么它的逆${R^{-1}\rvert-R^{-1}\mathbf{v}}$也一定是群中的元素,假如${R\rvert\mathbf{w}}$也是群中的元素,那么
\[\{R^{-1}\rvert-R^{-1}\mathbf{v}\}\{R\rvert\mathbf{w}\}=\{E\rvert R^{-1}\mathbf{w}-R^{-1}\mathbf{v}\}\]可以看到此时它必定是平移群$\mathbf{T}$的群元,因为其旋转操作部分为单位元$E$,群$\mathbf{G}$对应的布拉菲点阵的群对称点群为$\mathbf{P}$其必然包含点群操作$R$,如果$R^{-1}(\mathbf{w-v})$是$\mathbf{\Gamma}$的平移操作那么$\mathbf{w-v}$也是,这也就意味着任何一个与点群操作相关联的平移操作时平移操作群$\mathbf{T}$中一个分立的元素,因此可以将空间群$G$分解成平移群$\mathbf{T}$的左陪集表示
\[\mathbf{G}=\{R_1\rvert\mathbf{v}_1\}\mathbf{T}+\{R_2\rvert\mathbf{v}_2\}\mathbf{T}+\cdots+\{R_h\rvert\mathbf{v}_h\}\mathbf{T}\]对于点式空间群,所有的$\mathbf{v}_i=0$,但是对于非点式空间群,存在$\mathbf{v}_i\neq 0$.
$\mathbf{Q}$包含了陪集表示${R_i\rvert\mathbf{v}_i}$,h个元素$R_1,R_2,\cdots,R_h$构成了一个群$\mathbf{F}$,它与空间群$\mathbf{G}$是同形的,并且它也是$\mathbf{P}$的子群.对于点式空间群$\mathbf{F}$与$\mathbf{Q}$是一致的,h叫做群$\mathbf{G}$的宏观阶数(macroscopic order),它是群$\mathbf{T}$在$\mathbf{G}$中的index.
index$\rightarrow\frac{\rvert\mathbf{G}\rvert}{\rvert\mathbf{T}\rvert}$对应的正是空间群的阶数与不变子群阶数的商.
对于非点式空间群,在进行陪集分解的时候,在空间群操作的限制下非零矢量$\mathbf{v}$并不是任意的,如果点群操作$R$的阶数为$n$,那么${R\rvert\mathbf{v}}^n$也一定属于平移操作$\mathbf{T}$,也就是说
\[\mathbf{v}+R\mathbf{v}+\cdots+R^{n-1}\mathbf{v}\]必然是个平移操作,这也就限制了非点式空间群的数目是157个.
$\mathbf{T}$是$\mathbf{G}$的不变子群:如果${R\rvert\mathbf{v}}$是空间群$\mathbf{G}$的一个元素,${E\rvert\mathbf{t}}$是平移群$\mathbf{T}$的一个元素,那么满足
\[{R\rvert\mathbf{v}}{E\rvert\mathbf{t}}{R\rvert\mathbf{v}}^{-1}={R\rvert\mathbf{v}+R\mathbf{t}}{R^{-1}\rvert-R^{-1}\mathbf{v}}={E\rvert R\mathbf{t}}\]它是平移群的一个元素,因为$R\mathbf{t}$属于$\mathbf{\Gamma}$.
examplex
下面给出一个例子,如何通过一些等价的位置来确定空间群对应的操作算符的形式;\quad 通常会给出一般点和高对称点对应的等价位置.
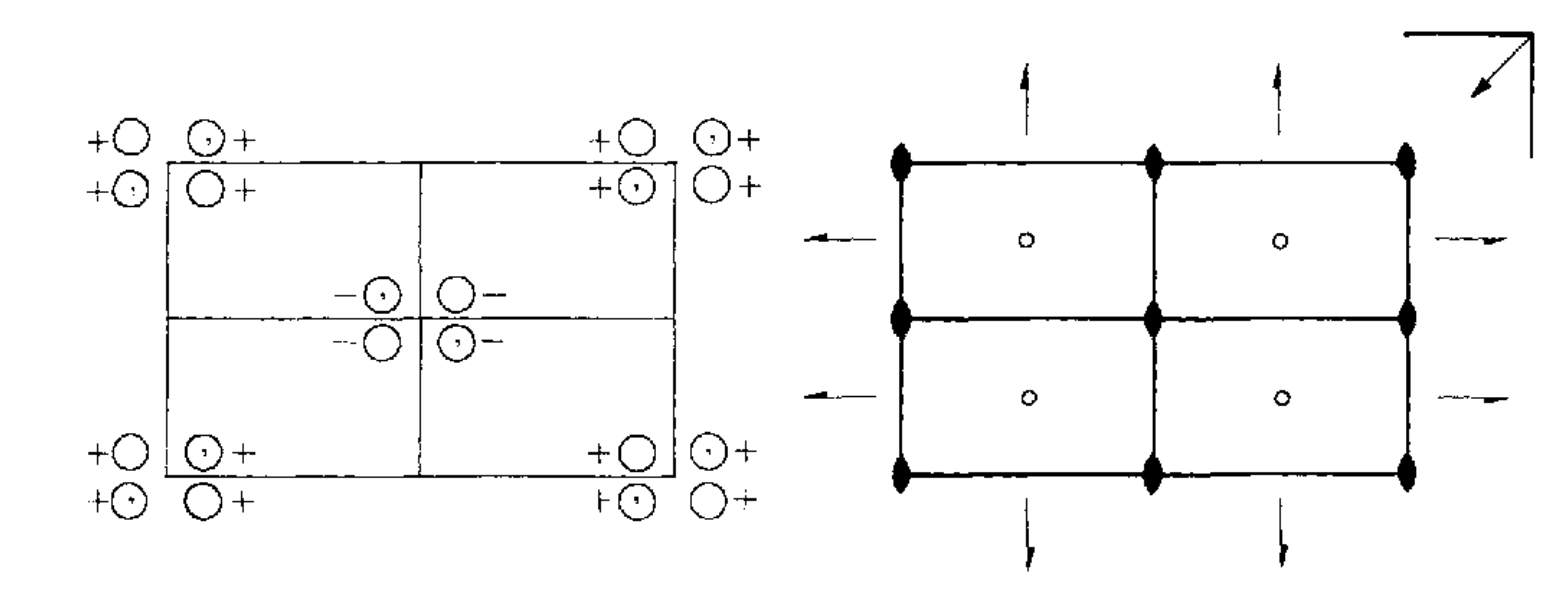

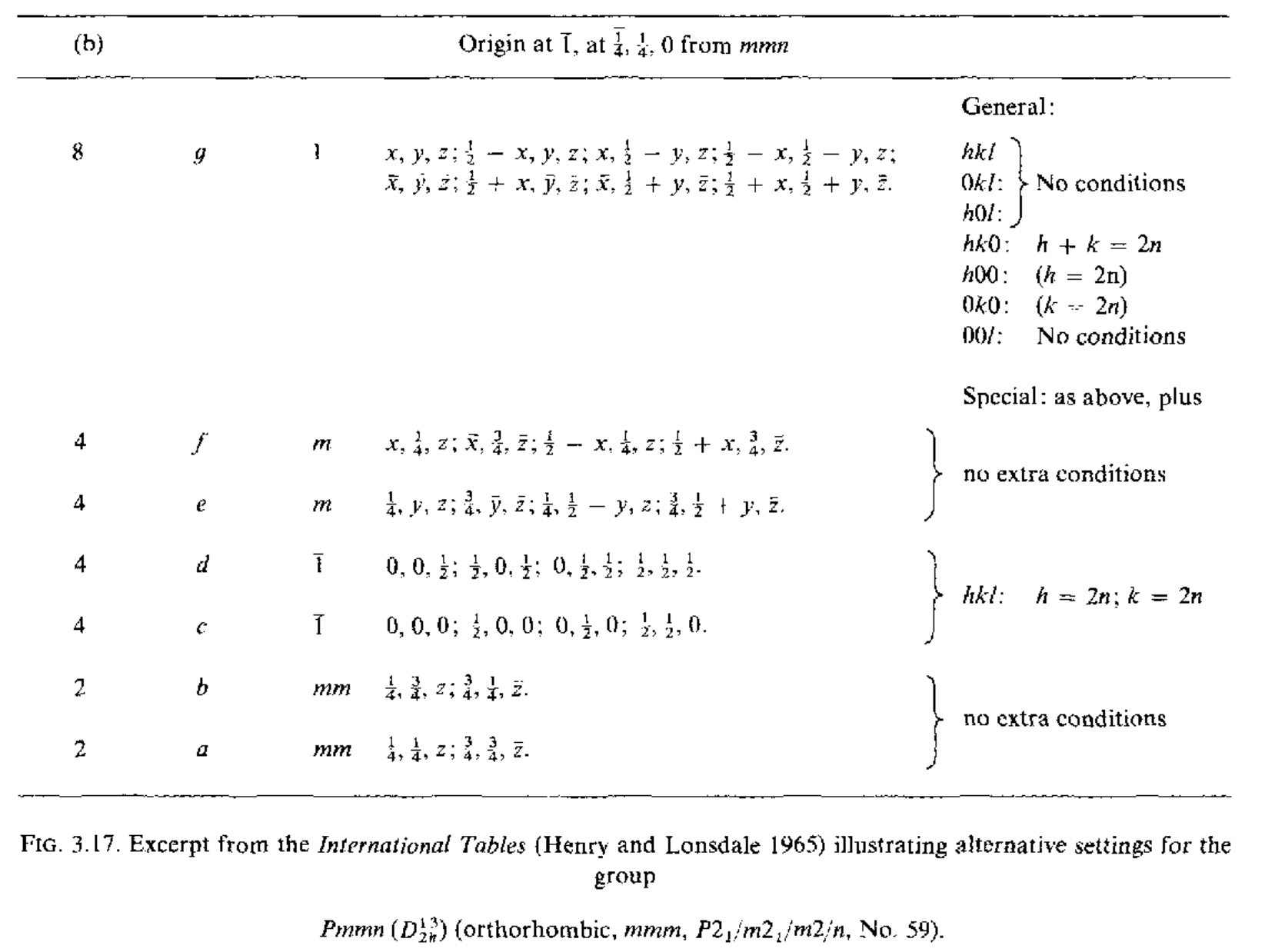
在(a)中的第一行,给出了空间群$Pmmm(D_{2h}^{13})$元胞中一般点$(x,y,z)$对应的等价位置,后面同样给出了高对称点(线)对应的等价位置,但这里先不考虑高对称点(线)的情况.对于一个一般的点$(x,y,z)$经过空间群操作${R_1\rvert\mathbf{v}_1}$之后可以有
\[\mathbf{r}_1^{'}=R_1\mathbf{r}_1+\mathbf{v}_1\]从上面的表中可以看到一般点的等价位置都有
\[\begin{equation}\begin{aligned}&x,y,z;\quad \bar{x},\bar{y},z;\quad \bar{x},y,z;\quad x,\bar{y},z;\quad \\ &\frac{1}{2}-x,\frac{1}{2}-y,\bar{z};\quad \frac{1}{2}-x,\frac{1}{2}+y,\bar{z};\quad \frac{1}{2}+x,\frac{1}{2}+y,\bar{z};\quad \frac{1}{2}+x,\frac{1}{2}-y,\bar{z};\end{aligned}\end{equation}\]这里的分数坐标时相对于元胞的边长.首先根据$\mathbf{r}^{‘}$来确定点群操作$R_1$,通过查表
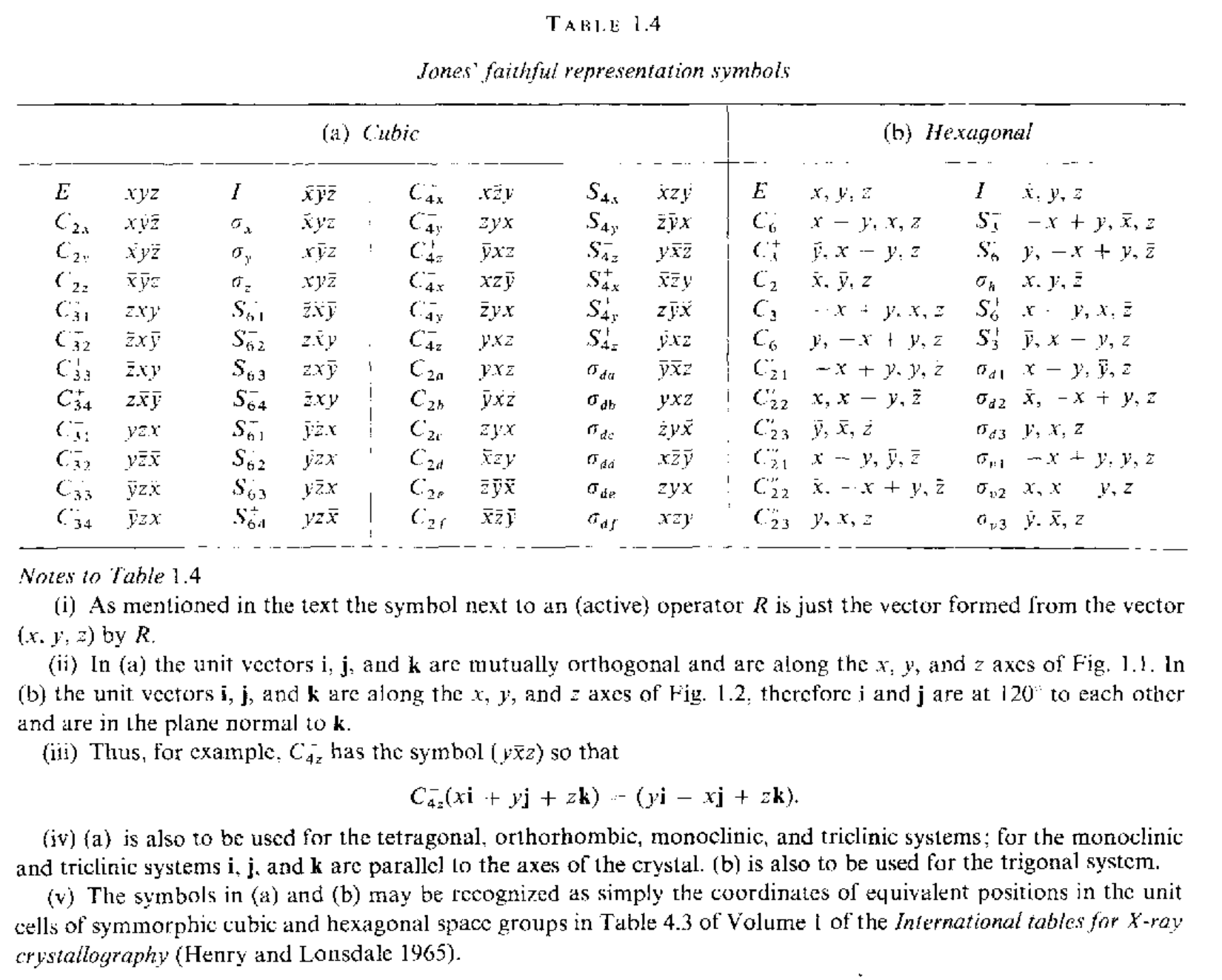
可以得到
\[\begin{equation}\begin{aligned}&E:xyz;\quad C_{2z}:\bar{x}\bar{y}z;\quad\sigma_x:x\bar{y}z;\quad\sigma_y:x\bar{y}z;\\ &I:\bar{x}\bar{y}\bar{z};\quad C_{2y}:\bar{x}y\bar{z};\quad\sigma_z:xy\bar{z};\quad C_{2x}:x\bar{y}\bar{z};\end{aligned}\end{equation}\]首先确定了点群部分的操作,对于primitive orthorhombic的布拉菲点阵,元胞基矢为
\[\mathbf{t}_1=(0,-b,0),\mathbf{t}_2=(a,0,0)\]上面后四个操作对应的平移矢量为$-\frac{1}{2}\mathbf{t}1+\frac{1}{2}\mathbf{t}_2$,对基矢加上一个整数倍可以得到$\mathbf{v}_1=+\frac{1}{2}\mathbf{t}_1+\frac{1}{2}\mathbf{t}_2$,从而可以得到空间群$Pmmm(D{2h}^{13})$的元素为
\[\begin{equation}\begin{aligned}&\{E\rvert 000\};\quad \{C_{2z}\rvert 000\};\quad\{\sigma_x\rvert 000\};\quad\{\sigma_y\rvert 000\};\\ &\{I\rvert\frac{1}{2}\frac{1}{2}0\};\quad\{C_{2y}\rvert\frac{1}{2}\frac{1}{2}0\};\quad\{\sigma_z\rvert\frac{1}{2}\frac{1}{2}0\};\quad\{C_{2x}\rvert\frac{1}{2}\frac{1}{2}0\}\end{aligned}\end{equation}\]在列举空间群的元素时,并不需要将所有的都罗列出来,只需要将群的生成元列举即可,空间群$Pmmm(D_{2h}^{13})$的生成元为
\[\{C_{2x}\rvert\frac{1}{2}\frac{1}{2}0\},\quad \{C_{2y}\rvert\frac{1}{2}\frac{1}{2}0\},\quad \{I\rvert\frac{1}{2}\frac{1}{2}0\}\]原点平移
下面来看一下原点平移对空间群操作算符的影响,假设$\mathbf{r}^{‘},\mathbf{r}$分别是新旧坐标位置,在旧坐标系$Ox_1y_1z_1$中操作算符维${R_1\rvert\mathbf{r}_1}$,在新的坐标系$Ox_2y_2z_2$相对旧坐标系有一个平移操作$+\mathbf{t}_0$,
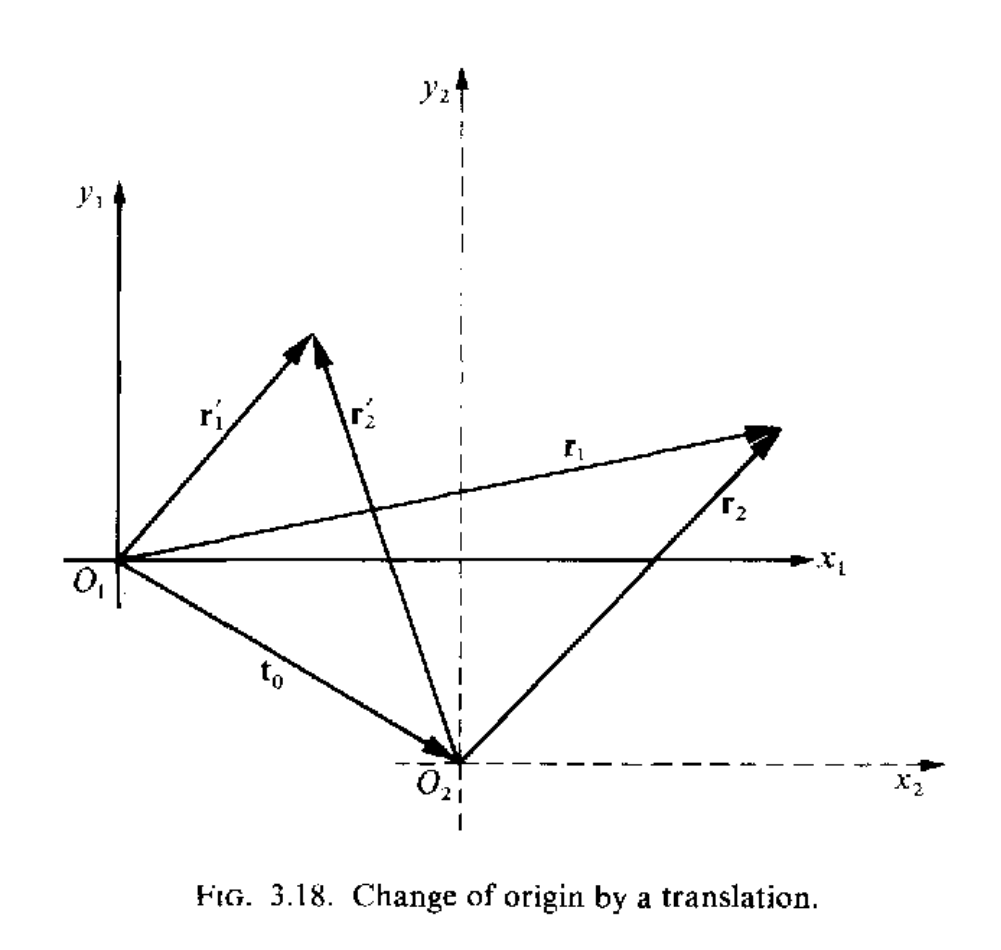
从图中可以看到
\[\mathbf{r}_1=\mathbf{t}_0+\mathbf{r}_2,\quad\mathbf{t}_1^{'}=\mathbf{t}_0+\mathbf{r}_2^{'}\]当${R_1\rvert\mathbf{v}_1}$作用在$Ox_1y_1z_1$中的时候
\[\mathbf{r}_1^{'}=R_1\mathbf{r}_1+\mathbf{v}_1\]在坐标系$Ox_2y_2z_2$中的操作为${R_2\rvert\mathbf{v}_2}$满足
\[\mathbf{r}_2^{'}=R_2\mathbf{r}_2+\mathbf{v}_2\]利用上面的关系来决定在${R_1\rvert\mathbf{v}_1}$下${R_2\rvert\mathbf{v}_2}$是如何变化的
\[\begin{equation}\begin{aligned}R_2\mathbf{r}_2+\mathbf{v}_2&=\mathbf{r}_2^{'}\\&=\mathbf{r}_1^{'}-\mathbf{t}_0\\&=R_1\mathbf{r}_1+\mathbf{v}_1-\mathbf{t}_0\\&=R_1(\mathbf{t}_0+\mathbf{r}_2)+\mathbf{v}_1-\mathbf{t}_0\\&=R_1\mathbf{r}_2+\mathbf{v}_1+R_1\mathbf{t}_1-\mathbf{t}_0\end{aligned}\end{equation}\] \[R_2\mathbf{r}_2+\mathbf{v}_2=R_1\mathbf{r}_2+\mathbf{v}_1+R_1\mathbf{t}_0-\mathbf{t}_0\]因此在坐标平移之后,对空间群操作的影响就是
\[R_2=R_1,\quad\mathbf{v}_2=\mathbf{v}_1+R_1\mathbf{t}_0-\mathbf{t}_0\] \[\{R_2\rvert\mathbf{v}_2\}=\{R_1\rvert\mathbf{v}_1+R_1\mathbf{t}_0-\mathbf{t}_0\}\]在前面的Fig13.7中就给出了空间群$Pmmm(D_{2h}^{13})$在两种不同的坐标下的操作,其对应的平移矢量为
\[\mathbf{t}_0=\frac{1}{4}\mathbf{t}_1-\frac{1}{4}\mathbf{t}_2\]下面给出230个空间群对应的生成元及其符号标记
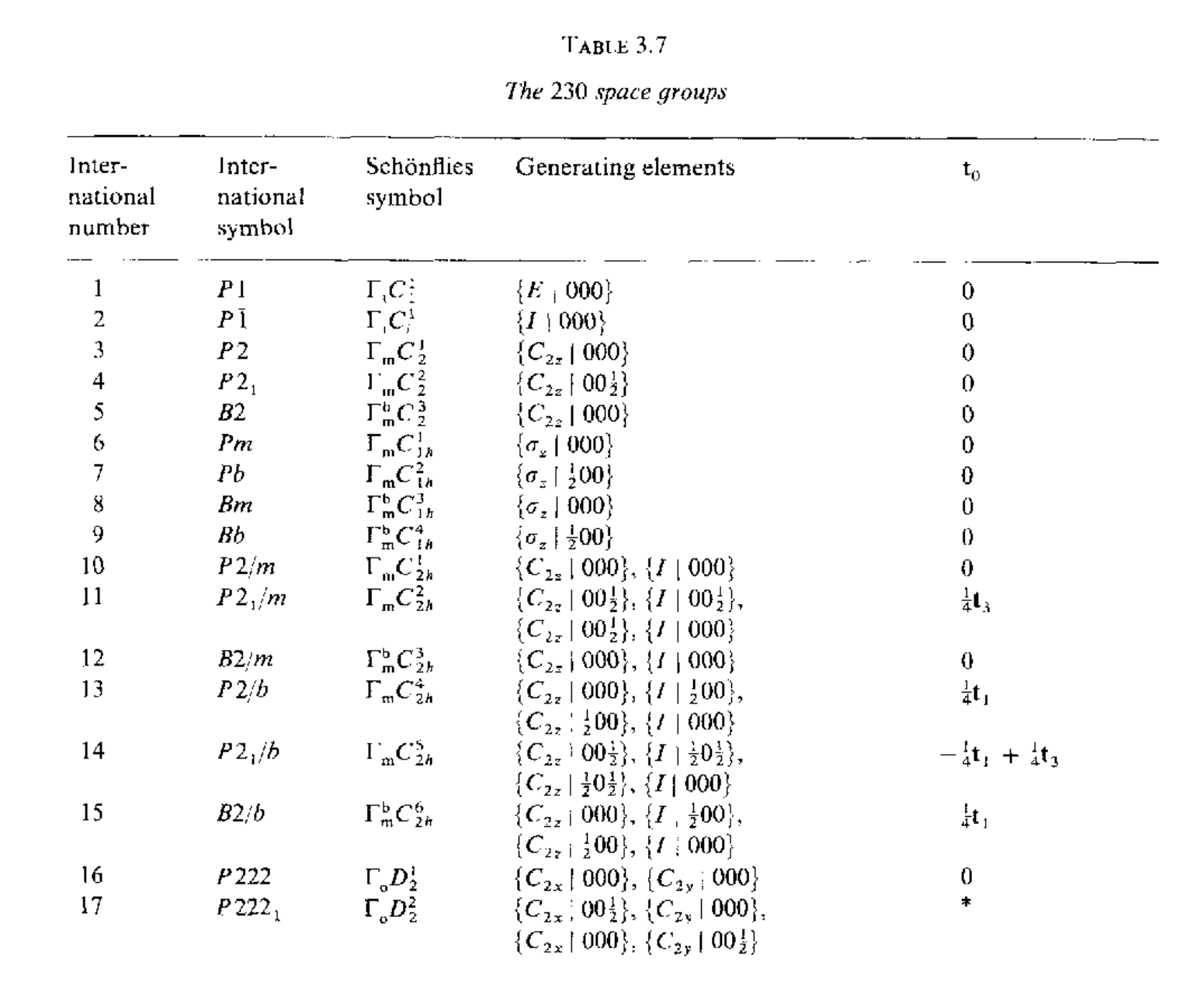





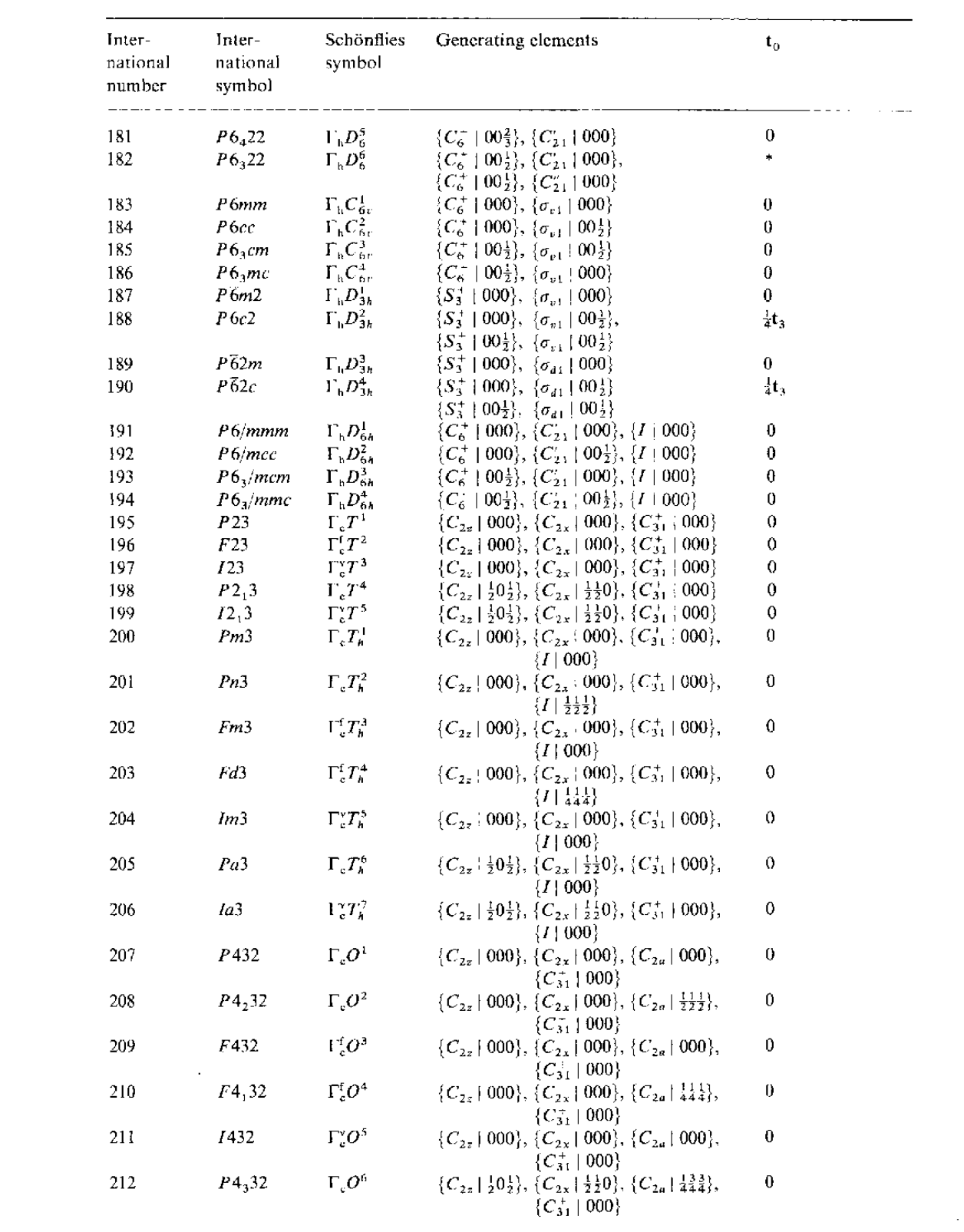
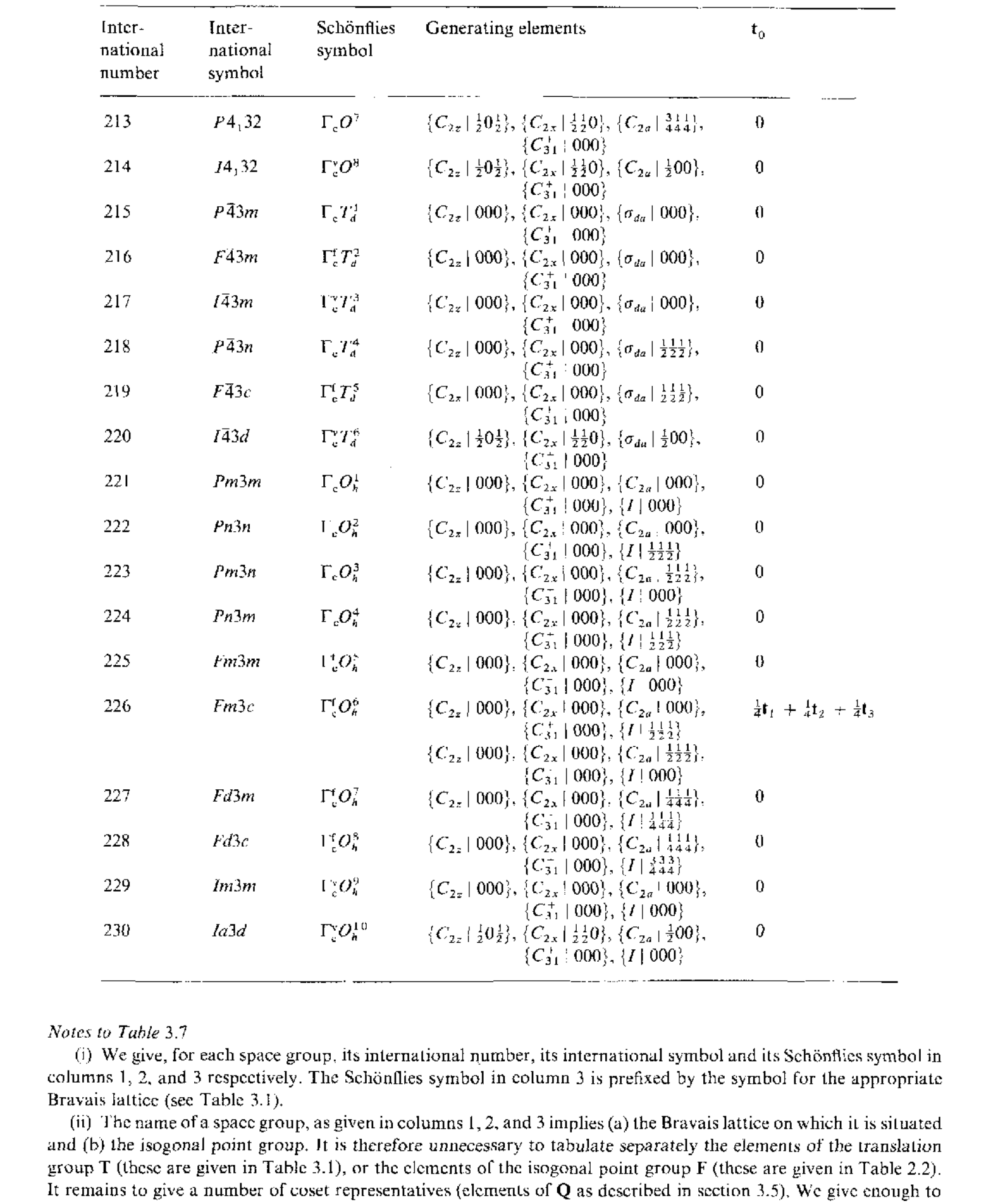

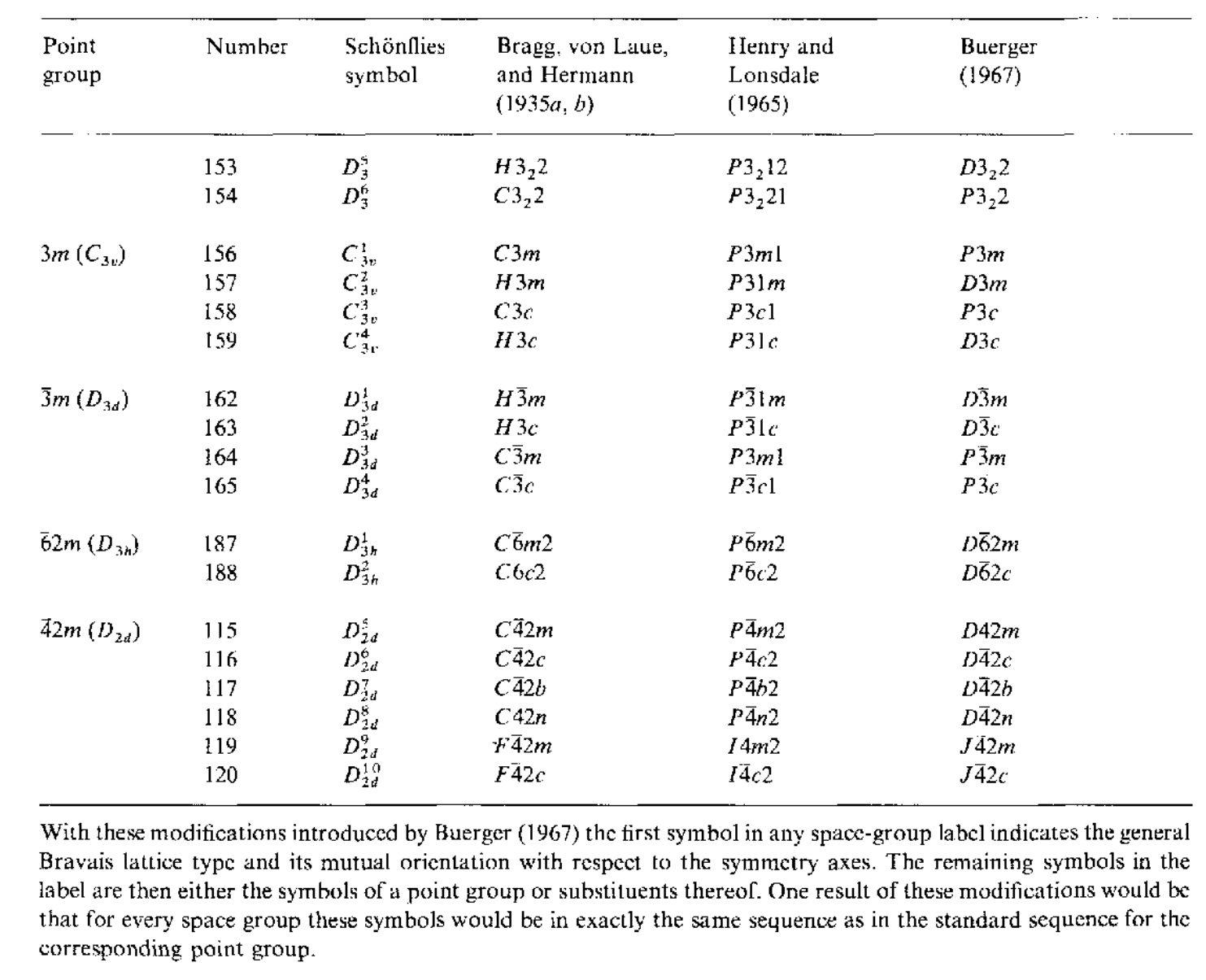
下面整理一下利用等价位置来得到对称操作的几何描述,${R_i\rvert\mathbf{r}_i}$对一般点的作用为
\[x^{'},y^{'},z^{'}=r_1+a_{11}x+a_{12}y+a_{13}z,r_2+a_{21}x+a_{22}y+a_{23}z,r_3+a_{31}x+a_{32}y+a_{33}z\]这里的$r_i$是分数,$a_{ij}=+1,-1,0$.
对于空间群$Pmmm(D_{2h}^{13})$可以发现在等价位置中$\frac{1}{2}+x,\frac{1}{2}-y,\bar{z}$意味着$a_{11}=+1,a_{22}=a_{33}=-1,r_1=r_2=\frac{1}{2},r_3=0$,剩余的$a_{ij}=0$,可以将其利用矩阵表示为
\[\begin{equation}\mathbf{M}(\{R_i\rvert\mathbf{r}_i\})=\left(\begin{array}{cccc}a_{11}&a_{12}&a_{13}&r_1\\a_{21}&a_{22}&a_{23}&r_2\\a_{31}&a_{32}&a_{33}&r_3\\0&0&0&1\end{array}\right)=(\mathbf{A},\mathbf{r}_i)\end{equation}\]这里矩阵$\mathbf{M}$作用在矢量$(x,y,z,1)^T$上,从Table1.4中可以得到所有的系数$a_{ij}$,从而也可以得到空间群的点群操作$R$,矩阵$\mathbf{A}$的特征标$\chi(\mathbf{A})$以及行列式$\det(\mathbf{A})$也可以由下表得出,这里的$C_n$表示$2\pi/n$的转动操作

如果$\det(\mathbf{A})=+1$那么这个对称元素要么是纯转动,要么是一个螺旋轴操作,下面就是来确定这个转动轴的方向或者螺旋轴矢量$\mathbf{w}$.如果$\mathbf{q}$是一个穿过原点且与螺旋轴操作轴平行的矢量那么其满足$\mathbf{Aq}=\mathbf{q}$,它确定了螺旋轴的方向,可以进行求解
\[(\mathbf{A}-E)\mathbf{q}=0\]为了确定螺旋轴矢量$\mathbf{w}$,对于螺旋轴后操作有
\[\{R_i\rvert\mathbf{r}_i\}\mathbf{q}=\mathbf{Aq}+\mathbf{r}_i=E\mathbf{q}+\mathbf{r}_i=\mathbf{q}+\mathbf{r}_i\]从而得到
\[\{R_i\rvert\mathbf{r}_i\}^2\mathbf{q}=\mathbf{q}+\mathbf{r}_i+\mathbf{Ar_i}\] \[\{R_i\rvert\mathbf{r}_i\}^n\mathbf{q}=\mathbf{q}+\mathbf{r}_i+\mathbf{Ar_i}+\mathbf{A^2r_i}+\cdots+\mathbf{A^{n-1}r_i}=\mathbf{q}+n\mathbf{w}\]因为在作用$n$次螺旋操作之后其等价于一个平移操作$n\mathbf{w}$.将上式重新组织就可以得到
\[\mathbf{w}=(1/n)(\mathbf{E}+\mathbf{A}+\mathbf{A^2}+\cdots++\mathbf{A^{n-1}})\mathbf{r}_i\]螺旋轴的方向自然可以通过$\mathbf{w}$来得到.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |