这里利用空间转动操作联系哈密顿量来推导一下如何对哈密顿量进行幺正变换从而实现对坐标系的转动,主要是Helical Higne Majorana Modes in Iron-Based Superconductor 这片文章中结果的一些推导。
这里考虑一个3D拓扑绝缘体
\[\begin{aligned} H_{0}(\mathbf{k})&=m(\mathbf{k})\Gamma_{5}+v(\sin k_{x}\Gamma_{1}+\sin k_{y}\Gamma_{2}+\sin k_{z}\Gamma_{3})\\ m(\mathbf{k})&=m_{0}-m_{1}(\cos k_{x}+\cos k_{y})-m_{2}\cos k_{z} \end{aligned}\]这里的$\Gamma$矩阵满足下面的关系
\[\begin{aligned} &\Gamma_{1}=\sigma_{x}\otimes s_{x}\quad\Gamma_{2}=\sigma_{x}\otimes s_{y}\quad\Gamma_{3}=\sigma_{x}\otimes s_{z}\\ &\Gamma_{4}=\sigma_{y}\otimes s_{0}\quad \Gamma_{5}=\sigma_{z}\otimes s_{0}\quad\Gamma_{ij}=\frac{1}{2i}[\Gamma_{i},\Gamma_{j}]\label{eq14} \end{aligned}\]这里的$\sigma_{i}$表示的轨道自由的,而$s_{i}$代表的是自旋自由度,当选取参数$v=1,m_{0}=-4,m_{1}=-2,m_{2}=1$,此时能带反转点在$Z$,将哈密顿量$H_{0}(\mathbf{k})$在这一点进行低能展开
\[H_{0}^{Z}(\mathbf{k})=v(k_{x}\Gamma_{1}+k_{y}\Gamma_{2}-k_{z}\Gamma_{3})+[\tilde{m}_{0}+\frac{m_{1}}{2}(k_{x}^{2}+k_{y}^{2})-\frac{m_{2}}{2}k_{z}^{2}]\Gamma_{5}\label{eq12}\]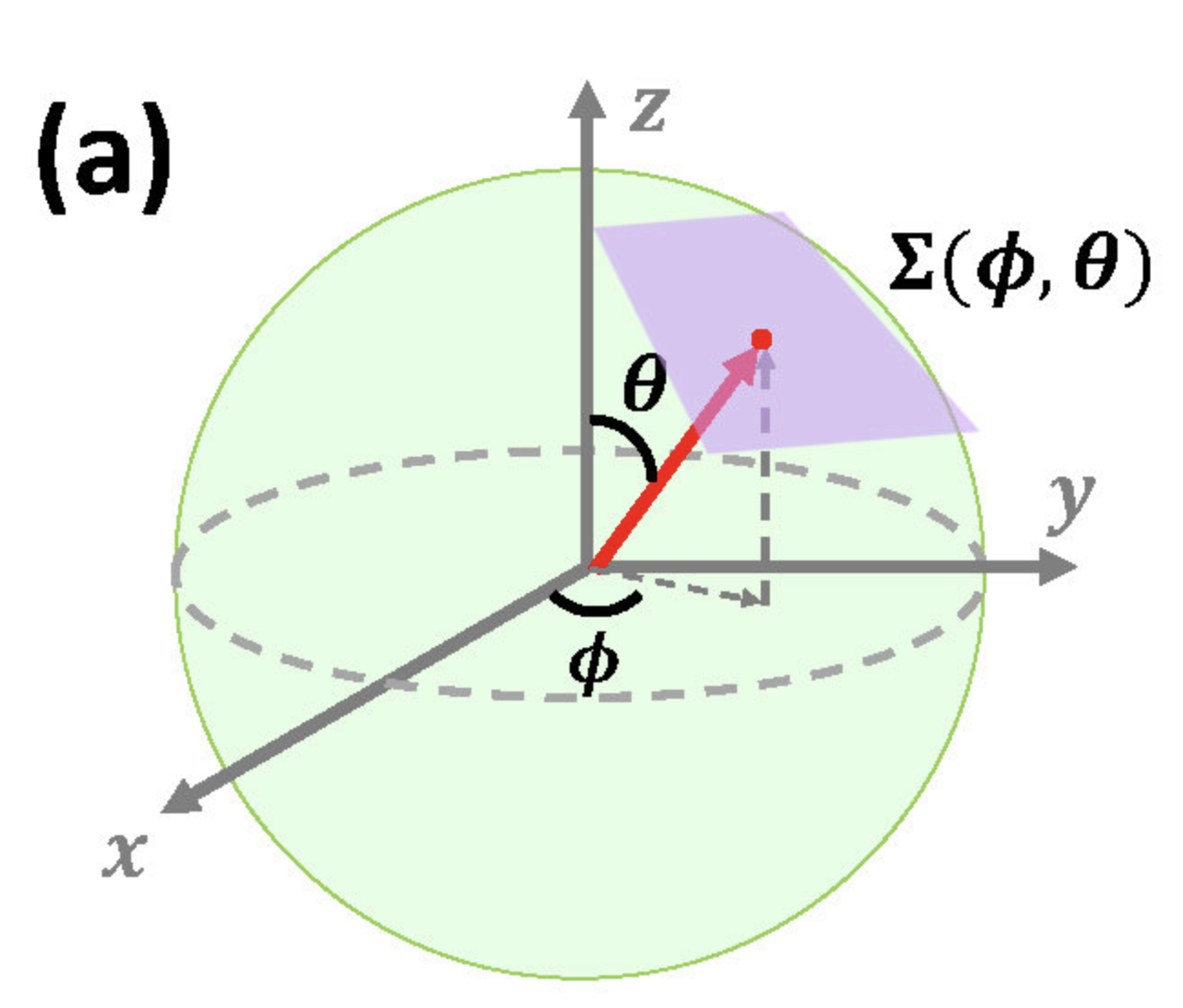
如上图所示,当考虑一个切面$\Sigma(\phi,\theta)$上的问题时,关注哈密顿量中的线性阶项即可以抓住问题的关键,忽略(\ref{eq12})中的二次项,得到
\[H_{0}^{Z}(\mathbf{k})=v(k_{x}\Gamma_{1}+k_{y}\Gamma_{2}-k_{z}\Gamma_{3})+\tilde{m}_{0}\Gamma_{5}\label{eq13}\]这里先分析哈密顿量(\ref{eq13})的形式,首先可以看到$\Gamma_{1,2,3}$中,轨道自由度均为$\sigma_{x}$唯一不同的就是其对应的spin自由度分别是$s_{x,y,z}$,而常数项$m_{0}\Gamma_{5}$并不与空间坐标$k_{i}$相关。
当考虑一个切面的时候,转动原来的$O-xyz$坐标系,利用前面已经介绍的欧拉转动,首先绕着$z$轴转动$\phi$角,再绕着$y$轴转动$\theta$角,利用欧拉转动表示为
\[{\bf k^{'}}=(k_{1},k_{2},k_{3})^{T}=R(\phi,\theta){\bf k}\]在前面的\ref{s22}节中已经知道了,{\color{blue!70}三维正当转动群SO(3)和SU(2)群之间是同态的,那么此时就可以将对空间$k_{i}$的转动操作,转移到$\Gamma_{i}$的变换中,只不过此时需要注意的是此时对应的是一个$4\times 4$的幺正矩阵,但是因为所有的$k_{i}$对应的$\Gamma_{i}$中,$\sigma_{i}=\sigma_{x}$都是相同的,所以这里就只需要确定$s_{i}$对于转动操作中,是如何组合的。}
这里需要再观察哈密顿量(\ref{eq13})的形式
\[H_{0}^{Z}(\mathbf{k})=v(k_{x}\Gamma_{1}+k_{y}\Gamma_{2}{\color{red}-k_{z}\Gamma_{3}})+\tilde{m}_{0}\Gamma_{5}\]这里可以看到,相对于$k_{x,y}$而言,$k_{z}$前面的系数是负号,为了和\ref{s22}中的分析互相吻合,这里进行一下变化
\[H_{0}^{Z}(\mathbf{k})=v(k_{x}\Gamma_{1}+k_{y}\Gamma_{2}{\color{red}+k_{z}\tilde{\Gamma}_{3}})+\tilde{m}_{0}\Gamma_{5}\quad {\color{red}\tilde{\Gamma}_{3}=-\sigma_{x}\otimes s_{z}}\label{eq15}\]当变化成形式(\ref{eq15})之后,因为常数项并不会随着坐标转动而发生变换,所以它始终是可以不用关心的,只需要关系与$k_{i}$耦合的项,此时发现这个形式就与前面\ref{s22}中分析的情况完全相同,只不过在利用\ref{s22}中的公式的时候,需要将$s_{z}\rightarrow -s_{z}$,因为在(\ref{eq15})中为了与(\ref{eq16})中的形式一致,进行了形式替换${\color{red}\tilde{\Gamma}{3}=-\sigma{x}\otimes s_{z}}$,从而引进了一个负号。下面就可以写出对于坐标空间中的欧拉转动,当将其转嫁到$\Gamma_{i}$矩阵上的时候,对应的幺正变换的形式。
对于绕$z$轴转动$\phi$角,对应的幺正矩阵为
\[e^{-i\frac{\phi}{2}(-\sigma_{0}\otimes s_{z})}=e^{i\frac{\phi}{2}\sigma_{0}\otimes s_{z}}\]对于绕$y$轴转动$\theta$角,对应的幺正矩阵为
\[e^{-i\frac{\theta}{2}\sigma_{0}\otimes s_{y}}\]因此最终可以得到幺正变换的矩阵为
\[U(\phi,\theta)=e^{-i\frac{\theta}{2}\sigma_{0}\otimes s_{y}}e^{i\frac{\phi}{2}\sigma_{0}\otimes s_{z}}\label{eq17}\]利用幺正变换$U(\phi,\theta)$可以得到$\tilde{H}{0}^{Z}(\mathbf{k})=U(\phi,\theta)H{0}^{Z}(\mathbf{k})U^{-1}(\phi,\theta)=\tilde{h}{0}+\tilde{h}{1}$
\[\begin{aligned} \tilde{h}_0&=-vk_3\Gamma_3+(\tilde{m}_0-\tilde{m}_2k_3^2)\Gamma_5\\ \tilde{h}_1&=v(k_1\Gamma_2+k_2\Gamma_2)+(\tilde{m}_{13}k_1k_3+\tilde{m}_1k_1^2+\frac{m_1}{2}k_2^2)\Gamma_5 \end{aligned}\]这里从形式上看,就是幺正变换$U(\phi,\theta)$作用在之后,将操作带来的效果归结到$k_{1,2,3}$上,仍保持$\Gamma_{i}$的形式,而$k_{1,2,3}$的表达式如下
\[\begin{aligned} k_1&=k_x \cos (\theta ) \cos (\phi )+k_y \cos (\theta ) \sin (\phi )-k_z \sin (\theta )\\ k_2 &=-k_x \sin\phi + k_y\cos\phi\\ k_3&=k_x \sin (\theta ) \cos (\phi )+k_y \sin (\theta ) \sin (\phi )+k_z \cos (\theta ) \end{aligned}\label{eq18}\]这里来说明如何通过欧拉转动来的(\ref{eq18})所反映的坐标系之间的变换关系,首先如果是一个右手螺旋的坐标系$O-xyz$,那么对应的欧拉转动为
\[{\bf k^{'}}=(k_{1},k_{2},k_{3})^{T}=R(\phi,\theta){\bf k}\]这里绕轴转动的旋转操作在实空间的形式在(\ref{eq19})已经给出了,这里再写一遍
\[R_{z}(\alpha)R_{y}(\beta)R_{z}(\gamma)=\left[ \begin{array}{ccc} \cos\alpha&-\sin\alpha&0\\ \sin\alpha&\cos\alpha&0\\ 0&0&1 \end{array} \right]\left[ \begin{array}{ccc} \cos\beta&0&\sin\beta\\ 0&1&0\\ -\sin\beta&0&\cos\beta \end{array} \right]\left[ \begin{array}{ccc} \cos\gamma&-\sin\gamma&0\\ \sin\gamma&\cos\gamma&0\\ 0&0&1 \end{array} \right]\]但是现在来看需要转动的哈密顿量
\[H_{0}^{Z}(\mathbf{k})=v(k_{x}\Gamma_{1}+k_{y}\Gamma_{2}{\color{red}-k_{z}\Gamma_{3}})+\tilde{m}_{0}\Gamma_{5}\]此时$z$轴的方向是指向负方向的,也就是此时的直角坐标为$O^{‘}-xyz$和上面的$O-xyz$互为镜像坐标系,所以此时的转动应该是对$O^{‘}-xyz$而言的,但是前面的欧拉转动的公式以及分析都是以$O-xyz$为基础进行的,所以就需要把这个转动换到$O^{‘}-xyz$的操作语言下,其实二者对应的关系很简单,如果是在$O^{‘}-xyz$中绕$z$转动$\phi$角,那么利用$O-xyz$的欧拉转动操作就是$R_{z}(-\phi)$。
当考虑一个切面的时候,转动原来的$O^{‘}-xyz$坐标系,利用前面已经介绍的欧拉转动,首先绕着$z$轴转动$\phi$角,再绕着$y$轴转动$\theta$角,利用欧拉转动表示为
\[{\bf k^{'}}=(k_{1},k_{2},k_{3})^{T}=R(-\phi,-\theta){\bf k}=R(-\phi,-\theta)(k_{x},k_{y},k_{z})\]对应的操作矩阵为
\[R_{y}(-\phi)\left[ \begin{array}{ccc} \cos (\phi ) & \sin (\phi ) & 0 \\ -\sin (\phi ) & \cos (\phi ) & 0 \\ 0 & 0 & 1 \\ \end{array} \right]\quad R_{z}(-\theta)=\left[ \begin{array}{ccc} \cos (\theta ) & 0 & -\sin (\theta ) \\ 0 & 1 & 0 \\ \sin (\theta ) & 0 & \cos (\theta ) \\ \end{array} \right]\]利用操作矩阵
\[\left[\begin{array}{c} k_{1}\\ k_{2}\\ k_{3} \end{array}\right]=\left[ \begin{array}{ccc} \cos (\phi ) & \sin (\phi ) & 0 \\ -\sin (\phi ) & \cos (\phi ) & 0 \\ 0 & 0 & 1 \\ \end{array} \right]\left[ \begin{array}{ccc} \cos (\theta ) & 0 & -\sin (\theta ) \\ 0 & 1 & 0 \\ \sin (\theta ) & 0 & \cos (\theta ) \\ \end{array} \right]\left[\begin{array}{c} k_{x}\\ k_{y}\\ k_{z} \end{array}\right]\]最终就可以得到(\ref{eq18})对应的表达式。
参考
1.Helical Higne Majorana Modes in Iron-Based Superconductor
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |