继续通过Wilson loop的理解,整理出如何计算Nested Wilson loop以及其物理含义。
Nested Wilson loop
在计算高阶拓扑绝缘体的时候,其边界态被打开了能隙,那么此时通过Wilson loop就不再能鉴别体系的拓扑性质了。但是此时Wilson loop也会打开gap,因为文献中已经证明了体系的边界态和Wilson loop其实是等价的,所以这个时候可以对Wilson loop重新建立一个关于Wilson loop的体边对应关系,这也就关系着这里想要讨论的Nested Wilson loop。
仍然先考虑一个2D系统,其动量分别为$k_x,k_y$,而且其对应的Wilson loop都是有gap的,如下图所示
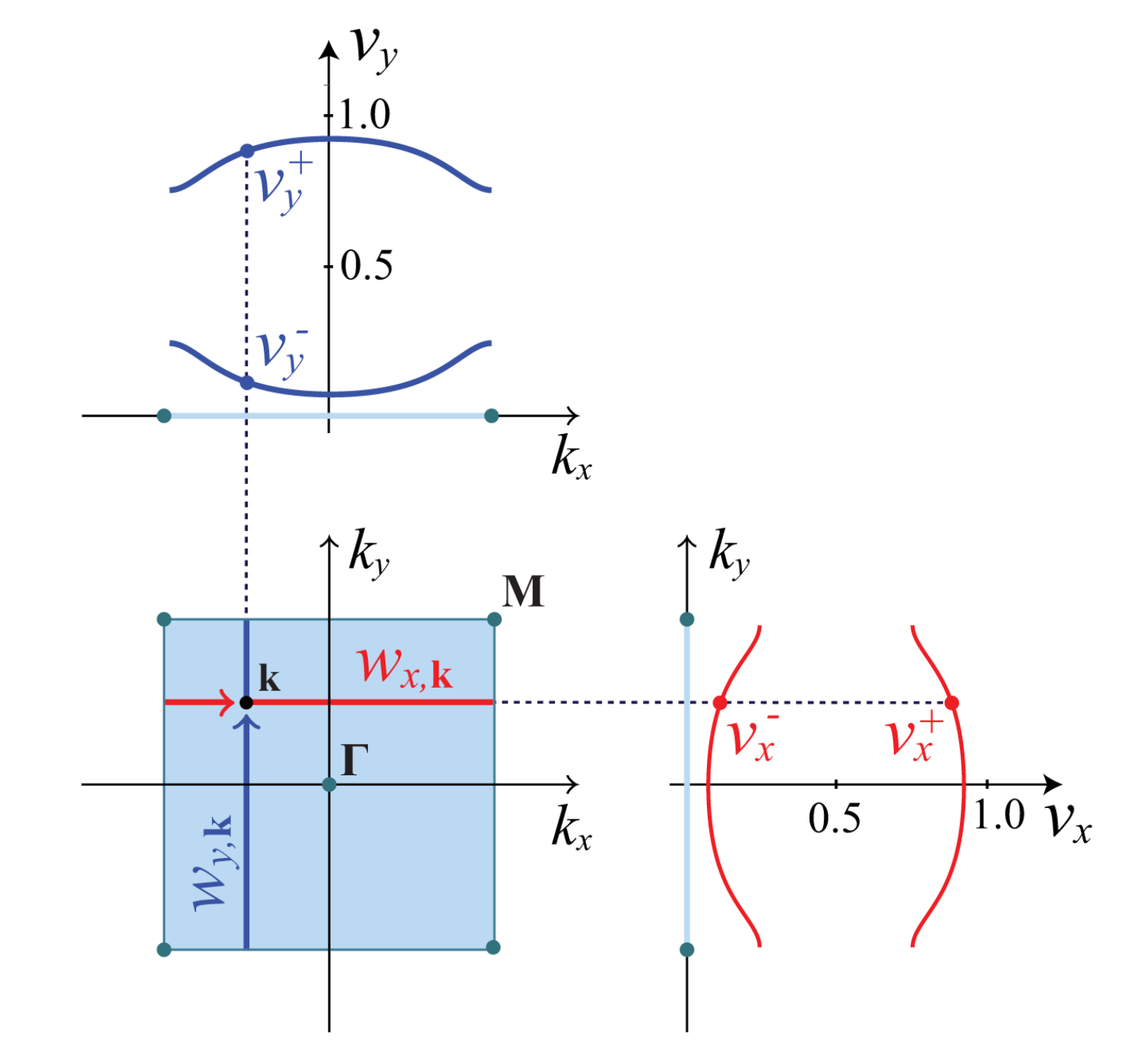
因为此时在$v_x=\frac{1}{2}$处存在Wannier gap,那么就可以将Wannier能带分成两个sector
\[\begin{align} \nu^-_x &= \{\nu^j_x(k_y), \text{ s.t. } \nu^j_x(k_y) \text{ is below the Wannier gap} \}\nonumber \\ \nu^+_x &= \{\nu^j_x(k_y), \text{ s.t. } \nu^j_x(k_y) \text{ is above the Wannier gap} \}.\nonumber \end{align}\]在之前的Blog中提到过,因为在求解Wilson loop时的矩阵$G$是幺正的,所以它的本征值只有mod 1才是well defined,所以可以将这里通过gap分开的两个能带分别进行标记$\nu^-_x \in [0,1/2)$ and $\nu^+_x \in [1/2,1)$,那么就可以利用这些孤立的Wannier能带来分别构建其对应的投影算符
\[\begin{align} P_{\nu_x}&=\sum_{j=1}^{N_W}\sum_{R_x, k_y} \rvert \Psi^j_{R_x,k_y}\rangle \langle \Psi^j_{R_x,k_y}\rvert\nonumber\\ &=\sum_{j=1}^{N_W} \sum_{n,m=1}^{N_{occ}} \sum_\mathbf{k} \gamma^\dagger_{n,\mathbf{k}}\rvert 0\rangle[\nu^j_{x,\mathbf{k}}]^n [\nu^{*j}_{x,\mathbf{k}}]^m \langle 0\rvert \gamma_{m,\mathbf{k}}, \end{align}\]这里的求和$\sum_i^{N_W}$就是对选定的Wannier sector中所有的Wannier能带进行求和,且$\nu_x = \nu^+x$ 或者 $\nu^-_x$。而$N_W$也就是这个sector中到底有几条Wannier能带,$R_x \in 0 \ldots N_x-1$是原胞的指标,离散的动量$k_y=\Delta{k_y} n_y$, 这里 $\Delta_{k_y}=2\pi / N_y$,$n_y$是沿着$y$方向的晶体动量,取值为$n_y\in 0,1,\cdots, N_y-1$。
在研究问题的时候,主要关注的就是在Wannier占据态空间$P_v$中的性质,就是因为Wannier sector的拓扑性质与边界态是密切相关的,所以此时就可以在这个新的子空间中来重新研究一遍位置算符在其中的性质,这里给出$y$方向的位置算符
\[\begin{align} \hat{y} &= \sum_{\mathbf{R}, \alpha} c^\dagger_{\mathbf{R},\alpha} \rvert 0\rangle e^{-i \Delta_{k_y} (R_y+r_{\alpha,y})} \langle 0\rvert c_{\mathbf{R},\alpha}\nonumber \\ &=\sum_{k_x,k_y,\alpha} c^\dagger_{k_x,k_y+\Delta_{k_y},\alpha} \rvert 0\rangle \langle 0\rvert c_{k_x,k_y,\alpha}, \end{align}\]将其投影到一个确定的Wannier sector $v_x$中,可以得到
\[\begin{align} P_{\nu_x} \hat{y} P_{\nu_x} =&\sum_{j,j'=1}^{N_W}\sum_\mathbf{k} \sum_{n,m,n',m'=1}^{N_{occ}} \gamma^\dagger_{n,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}\rvert 0\rangle \langle 0\rvert\gamma_{n',\mathbf{k}}\times\nonumber\\ &\left([\nu^j_{x,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}]^n [\nu^{*j}_{x,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}]^m \times \right. \nonumber\\ &\left. \langle u^m_{\mathbf{k}+{\mathbf{\Delta_{k_y}}}}\rvert u^{m'}_\mathbf{k}\rangle[\nu^{j'}_{x,\mathbf{k}}]^{m'}[\nu^{j'*}_{x,\mathbf{k}}]^{n'} \right). \end{align}\]这个表达式看起来在符号上会有些让人头疼,但是老老实实的将上面的投影算符作用到位置算符上,其实就可以得到这个结果,不过看起来还是有点复杂,可以定义一个Wannier band basis
\[\begin{align} \rvert w^j_{x,\mathbf{k}}\rangle = \sum_{n=1}^{N_{occ}}\rvert u^n_\mathbf{k}\rangle [\nu^j_{x,\mathbf{k}}]^n \end{align}\]这里的指标$j\in 1\cdots N_W$就是在标记Wannier sector中的Wannier能带指标,而且这些basis满足
\[\langle w^j_{x,\mathbf{k}}\rvert w^{j'}_{x, \mathbf{k}}\rangle=\delta_{jj'}\]也就是说对于不同Wannier band构成的这个basis才满足正交关系,通常情况下有
\[\langle w^j_{x,\mathbf{k}}\rvert w^{j'}_{x, \mathbf{q}}\rangle \neq \delta_{j,j'} \delta_{\mathbf{k}, \mathbf{q}}\]在这个新的表示下面,可以将在Wannier sector中投影的位置算符表示为
\[\begin{align} P_{\nu_x} \hat{y} P_{\nu_x} =&\sum_{j,j'=1}^{N_W}\sum_\mathbf{k} \sum_{n,n'=1}^{N_{occ}} \gamma^\dagger_{n,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}\rvert 0\rangle \langle 0\rvert\gamma_{n',\mathbf{k}}\times\nonumber\\ &\left([\nu^j_{x,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}]^n \langle w^j_{x,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}\rvert w^{j'}_{x,\mathbf{k}}\rangle[\nu^{j'*}_{x,\mathbf{k}}]^{n'} \right), \end{align}\]到这里看起来就是引入了一个basis,将表达式修改了一下,看起来不是那么复杂,后面将会看到,这个构建的basis时有重要作用的。这里看起来就是要在一个新的子空间中沿着$y$方向进行Wilson loop的计算,而且在$k_x$的表示下,这个算符是对角化的,表示为
\[\begin{align} P_{\nu_x} \hat{y} P_{\nu_x} =&\sum_{k_x,k_y} \sum_{n,n'=1}^{N_{occ}} \gamma^\dagger_{n,(k_x,k_y+ \Delta_{k_y})}\rvert 0\rangle \times \nonumber\\ &[F^{\nu_x}_{y,(k_x,k_y)}]^{n,n'} \langle 0\rvert\gamma_{n',(k_x,k_y)}, \end{align}\]这里的$F$矩阵为
\[\begin{align} [F^{\nu_x}_{y,(k_x,k_y)}]^{n,n'}&=\sum_{j,j'=1}^{N_W}[\nu^j_{x,(k_x,k_y+\Delta_{k_y})}]^n \times \nonumber\\ &\langle w^j_{x,(k_x,k_y+\Delta_{k_y})}\rvert w^{j'}_{x,(k_x,k_y)}\rangle[\nu^{j'*}_{x,{(k_x,k_y)}}]^{n'}. \end{align}\]到这里就很熟悉了,前面已经研究过Wilson loop的计算,此时为了对角化$P_{\nu_x} \hat{y} P_{\nu_x}$,计算沿着$y$方向的Wilson loop
\[\begin{align} [{\mathcal{W}}^{\nu_x}_{y, \mathbf{k}}]^{n,n'} &= F^{\nu_x}_{y,\mathbf{k}+N_y {\mathbf{\Delta_{k_y}}}} \ldots F^{\nu_x}_{y,\mathbf{k}+ {\mathbf{\Delta_{k_y}}}} F^{\nu_x}_{y,\mathbf{k}}\nonumber\\ &= [\nu^j_{x,\mathbf{k}+N_y{\mathbf{\Delta_{k_y}}}}]^n [\tilde{\mathcal{W}}^{\nu_x}_{y,\mathbf{k}}]^{j,j'}[\nu^{j'*}_{x,\mathbf{k}}]^{n'}\nonumber\\ &= [\nu^j_{x,\mathbf{k}}]^n [\tilde{\mathcal{W}}^{\nu_x}_{y,\mathbf{k}}]^{j,j'}[\nu^{j'*}_{x,\mathbf{k}}]^{n'}, \end{align}\]那么就可以得到在Wannier sector $v_x$上沿着$y$方向的Wilson loop $\tilde{\mathcal{W}^{v_x}_{y,\mathbf{k}}}$,它是在Wannier band basis下面定义的
\[\begin{align} [\tilde{\mathcal{W}}^{\nu_x}_{y,\mathbf{k}}]^{j,j'} =& \langle w^j_{x,\mathbf{k}+N_y{\mathbf{\Delta_{k_y}}}}\rvert w^{r}_{x,\mathbf{k}+(N_y-1) {\mathbf{\Delta_{k_y}}}}\rangle \times \nonumber\\ &\langle w^{r}_{x,\mathbf{k}+(N_y-1) {\mathbf{\Delta_{k_y}}}}\rvert \ldots \nonumber\\ &\dots \rvert w^{s}_{x,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}\rangle \langle w^s_{x,\mathbf{k}+{\mathbf{\Delta_{k_y}}}}\rvert w^{j'}_{x,\mathbf{k}}\rangle. \end{align}\]这里$r,\cdots,s\in 1,\cdots,N_W$表示对Wannier sector中所有的Wannier能带求和。
通过上面的分析可以确定,$N_W<N_{\rm occ}$,所以在计算$[\tilde{\mathcal{W}}^{\nu_x}_{y,\mathbf{k}}]^{j,j’}$的时候,也是只需要在占据态空间中计算就可以了。在前面的符号标记中,用$v_x$表示了Wannier能带上沿着$x$方向的Wannier本征值,这里利用$v_y^{v_x}$表示在Wannier sector $v_x$上沿着$y$方向其对应Wilson loop的本征值,那么对角化的Wilson loop表示为
\[\begin{align} \tilde{\mathcal{W}}^{\nu_x}_{y,\mathbf{k}} \rvert \nu^{\nu_x,j}_{y,\mathbf{k}}\rangle = e^{i 2\pi \nu^{\nu_x,j}_y(k_x)} \rvert \nu^{\nu_x,j}_{y,\mathbf{k}}\rangle \end{align}\]这里$j\in 1\cdots N_W$表示的仍然是Wannier sector中Wannier能带的指标,此时可以得到在$k_x$位置处,在Wannier sector $v_x$中对应的极化就是将所有$N_W$个Wannier能带贡献的位相$v_y^{v_x}(k_x)$进行求和
\[\begin{align} p^{\nu_x}_y(k_x) = \sum_{j=1}^{N_{\nu_x}} \nu^{\nu_x,j}_y(k_x) \text{mod 1}. \end{align}\]同样可以将其表示为
\[\begin{align} p^{\nu_x}_y(k_x) = -\frac{i}{2\pi} \text{Log Det}[\tilde{\mathcal{W}}^{\nu_x}_{y,\mathbf{k}}]. \end{align}\]体系总的极化为
\[\begin{align} p^{\nu_x}_y = \frac{1}{N_x} \sum_{k_x} p^{\nu_x}_y(k_x). \end{align}\]在热力学极限下,可以将其重新表述
\[\begin{align} p^{\nu_x}_y &=-\frac{1}{(2\pi)^2} \int_{BZ} \text{Tr} \left[\tilde{\mathcal{A}}^{\nu_x}_{y,\mathbf{k}}\right] d^2\mathbf{k} \end{align}\]这里的Berry联络就是定义在Wannier能带$v_x$上面的,其分量形式为
\[\begin{align} [\tilde{\mathcal{A}}^{\nu_x}_{y,\mathbf{k}}]^{j,j'} = -i \langle w^j_{x,\mathbf{k}}\rvert \partial_{k_y} \rvert w^{j'}_{x,\mathbf{k}}\rangle, \end{align}\]这里$j,j’\in 1,\cdots N_W$要遍历Wannier sector中所有的Wannier能带。其实也就是要计算Wannier能带上的Berry位相,最终就可以得到电四极矩。
所以通常所研究的Nested Wilson loop,其实也就是要在新的Wannier basis下面再计算Berry位相。
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |