最近正好有些空闲的时间，发现自己对拓扑中的一些理解并不深刻，正好借这个机会重新学习一下，加深自己对其中内容的理解，也能让自己之后的研究走的更远。

Andreev reflection

要理解通过Majorana模式时电导是如何工作的，我们首先必须了解电荷是如何从金属铅转移到超导体的。一般来说，这种转移是通过一种叫做Andreev反射的机制进行的。在我们讨论Majorana零模的电导特征之前，了解一下Andreev反射是什么是有用的。让我们考虑以下两个电极的简单电路:

一个电极是普通金属，另一个是超导体，它们的电压差为$V$。在普通金属和超导体之间的界面(简称NS界面)有一个势垒。我们特别感兴趣的是，与超导体中的能隙$eV < \Delta$相比，电压差非常小的情况，其中$e$是电子的电荷。当电子到达超导体的界面时会发生什么？超导体在费米能级附近没有能量不超过$\Delta$的状态，电压也不足以提供这种能量差，此时电流如何变化？为了理解这一点，首先仔细地观察到达超导体界面的电子。有两种可能发生的过程，正常反射和Andreev反射。在正常的反射中，电子只是在与超导体的界面处被反射：

正常反射时，左电极到右电极没有净电荷转移。因此，这个过程不贡献任何净电流。显然，正常的反射甚至不需要超导体，如果右电极不是超导体，同样会发生反射。

相反，Andreev反射是NS界面特有的。在Andreev反射中，一个电子被超导体转化为空穴，在超导体中形成一个库珀对

你可以看到，一个$2e$的净电荷从左电极转移到右电极，在低电压下，Andreev反射是唯一负责电流的过程。在超导能隙之上，入射电子进入超导体的$eV > \Delta$传输也有助于产生电流。这里可以把Andreev反射看作是一个传输问题。由于超导体的存在，电子和空穴都参与了普通金属铅中的电荷转移。从概念上讲，可以想象把左边的电极分成两条，一条只带电子，另一条只带空穴。这两条引线由超导体连接，超导体将第一条引线中的传入电子转换为第二条引线中的输出空穴，反之亦然：

有了这张图，就能理解Andreev反射和通过双势垒的传输问题非常相似。

我们称$r_{eh}$为Andreev反射的振幅。它的绝对值平方，$\rvert r_{eh}\rvert ^2$，是来自普通金属的电子被Andreev反射成空穴的概率。一旦我们知道了$r_{eh}$，我们就可以计算电导$G(V)$，它与小电压$V$的响应电流$I$有关，$G(V) = dI/dV$。电导由下式给出:

\[G(V)=2G_0\rvert r_{eh}\rvert ^2.\]

这里不推导这个方程，因为它可以直观地理解。电导与Andreev反射的概率$\rvert r_{eh}\rvert ^2$成正比，因为我们知道在低电压下，这是将电荷从左电极转移到右电极的唯一过程。前面的因子$2$是由于每个Andreev反射转移一个Cooper对的电荷$2e$。最后，$G_0=e^2/h$是电导量子，它是将电流与电压联系起来的基本比例常数。

Andreev reflection off a Majorana zero mode

现在已经了解了传统的NS界面，接下来看看如果超导体是拓扑的会发生什么：

可以想象超导电极现在是一个拓扑相的纳米线，正如前面研究的。因为超导体是拓扑的，在NS界面有一个Majorana模式，它的波函数将通过势垒“泄漏”一点到普通金属中。当然，也会有第二个Majorana模式，但是我们把它放在离NS界面足够远的地方，这样它就不会在传输中起作用。那么此时可以问一个问题，界面上的Majorana模式是否改变了Andreev反射特性？答案是肯定的，而且是以一种相当激烈的方式。首先回到Andreev反射作为通过双势垒的传输过程的图像，这里关键的区别是，马约拉纳模现在作为两个势垒之间的束缚态(Andreev bound state)出现：

在量子力学的双势垒问题中，你可以在束缚态存在的情况下有共振传输。这意味着，如果入射电子的能量与束缚态的能量相匹配，则$\rvert r_{eh}\rvert ^2$通过势垒的概率将显著提高。在我们的例子中，入射电子的能量是$V$，而束缚态Majorana模的能量是零。因此，在$V=0$处Majorana模式的存在导致NS界面的电导中有一个出现谐振峰。

Quantization of the Majorana resonance

观察谐振峰是我们所知道的测量马约拉纳零模存在的最直接方法。然而，与Majorana模式相关的共振的存在并不一定就是拓扑的特证，因为隧穿到任何低能束缚态都会产生共振(这里的束缚态可能不是零能束缚态)。有什么特别的东西把Majorana共振和其他共振区别开来吗？这里来比较NS界面的电导在超导体为平庸和拓扑的情况下会发生什么，看看电导是如何随着我们改变隧道势垒强度而变化的。

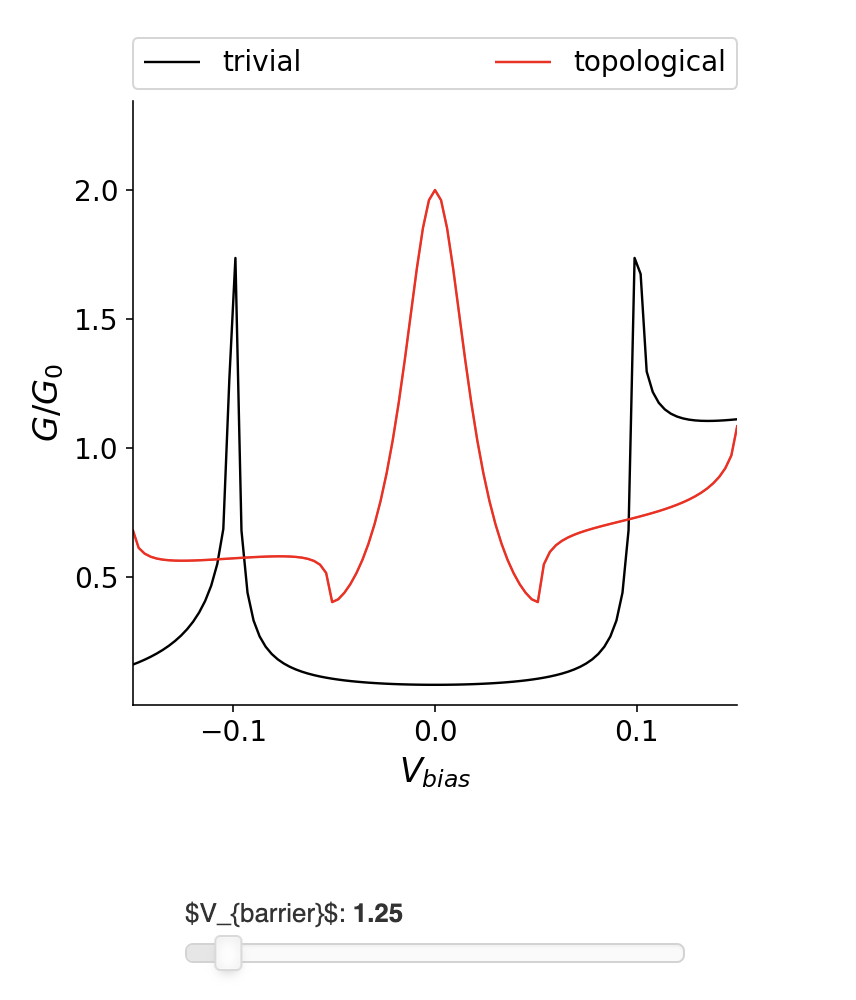
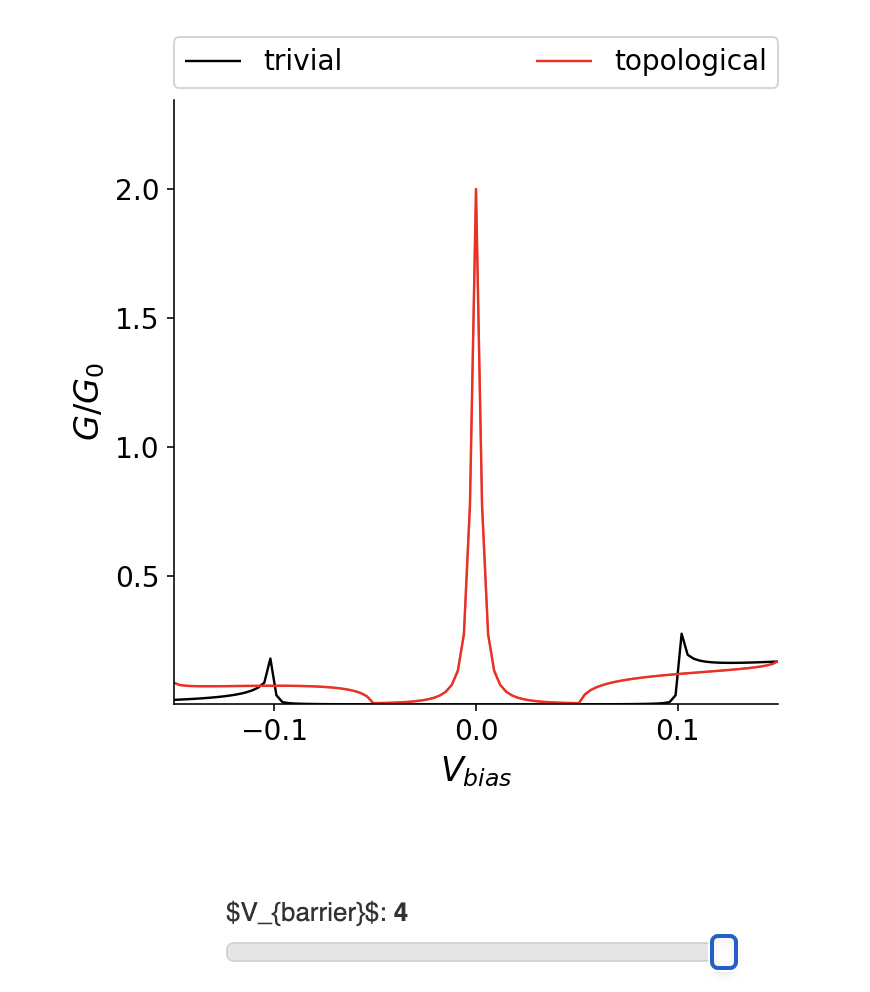
我们看到了一个非常robust且稳定的特征： Majorana共振的峰值高度被量化为$2G_0$，与电压势垒的强度无关。从上面的公式，这意味着如果一个Majorana存在，就会有$\rvert r_{eh}\rvert ^2=1$，也就是说我们有完美Andreev反射。要理解为什么它是robust的，我们需要超越上面的卡通描述。

Reflection matrix of a normal metal-superconductor interface

在量子力学上，我们可以把通过NS界面的传输描述为散射问题。输入波函数$\Psi_\textrm{in}$在左电极中传播，直到它被反射回与超导体的界面，变成输出波函数$\Psi_\textrm{out}$。由于超导体的存在，入射和出射态都可以是电子$\Psi_e$或空穴$\Psi_h$。在零能量时，它们通过粒子空穴对称性相互联系：

\[\Psi_e(E) = \mathcal{P}\,\Psi_h(-E)\,\]

反射使得入射波和入射波之间的存在线性关系：

\[\Psi_\textrm{out} = r(V) \,\Psi_\textrm{in}\,\] \[r(V)=\left(\begin{array}{cc}r_{ee}&r_{eh}\\r_{he}&r_{hh}\end{array}\right).\]

矩阵$r$称为反射矩阵。它的复数矩阵元 $r_{ee}$和$r_{eh}$跟别表示入射电子的正常反射和Andreev反射振幅，$r_{hh}$和$r_{he}$则表示入射空穴的正常反射和Andreev反射振幅 。(为了简洁起见，我们没有明确地写出每一个依赖于$V$的值)。如果体系有多个入射的电子态(在我们的例子中由于自旋有两个)，此时反射矩阵$r$的所有每个元素就都会包含额外的自由度，成为矩阵形式。这些反射系数描述了入射态和出射状态之间的所有可能的散射。

由于$eV\ll \Delta$的状态在超导体中不存在传播波(在表面很短的距离处就会衰减)，因此$\Psi_\textrm{out}$和$\Psi_\textrm{in}$之间的反射过程是幺正的，反射矩阵满足$r^\dagger r=1$。这意味着

\[\rvert r_{ee}\rvert ^2+\rvert r_{eh}\rvert ^2 = \rvert r_{he}\rvert ^2+\rvert r_{hh}\rvert ^2 = 1\,.\]

这是一种数学方法，说明到达界面的电子(或空穴)除了正常反射或Andreev反射外没有其他选择。这里可以发现并没有关注体系的对称性，那么是否可以在$r$中添加其他约束，以帮助区分Majorana模式的任何特征？就像之前所做的，利用了粒子空穴对称性。这里就尝试使用对称性和拓扑来研究反射矩阵$r$。因为在现在设计的电路中涉及超导体，所以我们必须在这个问题中考虑粒子-空穴对称性。

为了显式地推导反射系数$r$，可以直接从NS系统的BdG哈密顿量出发，求解出能量$V$。但这个工作会很繁琐，这里并不会这样做，但是实际上还是可以利用粒子空穴对称性来研究它对反射系数r的限制。首先，粒子空穴对称操作会交换了波函数的电子和空穴部分的分量，因此它涉及到作用于$\Psi_\textrm{in}$或$\Psi_\textrm{out}$的泡利矩阵$\tau_x$。其次，它是一个反幺正操作，所以它涉及到复共轭操作。第三，它改变了能量的符号，将$V$变成$-V$。因此，我们得到反射矩阵的如下对称性：

\[\tau_x r^*(-V) \tau_x = r(V)\,.\]

因为存在粒子空穴对称性，此时反射矩阵关于能量$V$是对称的，最有趣的是在$V=0$的这一点：

\[\tau_x r^*_0 \tau_x = r_0 \,.\]

这里定义了$r_0\equiv r(V=0)$。对称性对$r$的此时就说完了，除此之外还要考虑体系的拓扑性质。

Topological invariant of the reflection matrix

Majorana零模是拓扑超导体处在拓扑相中的结果，它的存在取决于体边对应关系。那么能否在反射系数$r_0$中找到跟体边对应相关的结果吗？研究发现，具有粒子空穴对称性的体系，此时反射矩阵$r$也有自己的拓扑方式。它们的拓扑不变量是

\[Q = \det\,r_0\,.\]

同样，我们不会“推导”这个方程，而是说服自己这个表达式是正确的。

首先，幺正矩阵，比如$r_0$，它的行列式总是一个具有单位范数的复数，因此$\rvert \det r_0\rvert =1$。其次，由于粒子空穴对称性，行列式为实数：

\[\det r_0 = \det (\tau_x r^*_0\tau_x) = \det r_0^*=(\det r_0)^*\]

因此，$\det r_0 = \pm 1$。可以发现在具有粒子空穴对称性的时候，这个量同样只有两个取值，像Kitaev链中的Pfaffian一样。由于$r_0$的行列式只是由幺正性和粒子空穴对称性所决定的，因此在NS界面的属性发生变化时，它的行列式不能从$+1$变为$-1$。实际上可以通过改变界面上势垒的高度，发现它并不会影响反射系数$r_0$的行列式。

能使得反射系数的行列式改变符号的唯一方法是关闭超导电极中的能隙。如果这超导体的能隙变为零，那么来自普通金属的入射电子就不可能只发生正常反射或安德烈夫反射。它也可以直接以电子的形式进入超导电极。因此反射矩阵不再包含在界面上发生的所有可能的过程，它不再是幺正的，此时行列式的符号就会发生变化。因此$Q=\det r$此时是一个很好的拓扑不变量，此时可以得到

\[Q=\rvert r_{ee}\rvert ^2-\rvert r_{eh}\rvert ^2\equiv\pm 1\,.\]

我们已经知道，幺正性要求

\[\rvert r_{ee}\rvert ²+\rvert r_{eh}\rvert ²=1\]

这两个条件都成立的可能性只有两种：$\rvert r_{ee}\rvert =1$(完美正常反射)或$\rvert r_{eh}\rvert =1$(完美Andreev反射)。

如果没有发生相变，情况就不会改变。因此，在这种情况下，Majorana零能模的量子化电导在拓扑上是稳健的，并且实际上在隧穿极限之后仍然存在。

Flux-induced fermion parity switch in topological superconductors

那么，如何在实验上直接探测拓扑超导体的Pfaffian拓扑不变量？之前在Kitaev模型中介绍过一个思想实验，通过改变键间hopping的符号，可以探索Majorana模的体边对应关系。拓扑不变量的变化就对应着Majorana费米子宇称的切换，这是因为跨越Kitaev结的尾端时，相邻格点之间的hopping大小$t$的符号改变的结果：

\[t\rightarrow -t.\]

事实证明，通过超导环引入磁通(类似于Aharonov-Bohm效应，也可以获得跨越结的时候，hopping符号发生变化。这个特殊键可以在Josephson结中实现，就是利用一个绝缘的势垒将Kitaev环在中间打断，如下图所示:

磁通量是如何进入哈密顿量的？通过使用Peierls替换将磁场引入晶格哈密顿量中，磁通量$\Phi$可以通过简单地改变环中跨过Kitaev链端点结处的跳变相位来解释:

\[t\,\to\,t\,\exp (i\phi/2).\]

这里，$\phi = 2\pi\Phi/\Phi_0$ 通常称为跨结的超导相位差，$\Phi_0=2e/h$ 是超导磁通量子。 请注意，当 $\Phi=\Phi_0$ 时，跳跃改变符号：$t\,\to\, \exp (i\pi) t = -t$，与前面在Kitaev 环中在尾端实现hopping反号是完全一致的。因此，磁通量子$\Phi=\Phi_0$的引入，改变了hopping

\[t\rightarrow te ^{i\phi}=-t\]

的符号，正如之前讨论的那样，这改变了拓扑超导体基态的费米子的宇称。这个费米子奇偶开关与在Josephson结处耦合的一对马约拉纳模有关(如上图所示)。

为了清楚地了解这是如何发生的，让我们看看拓扑超导环的能谱作为磁通量的函数，用之前讨论的纳米线模型得到：

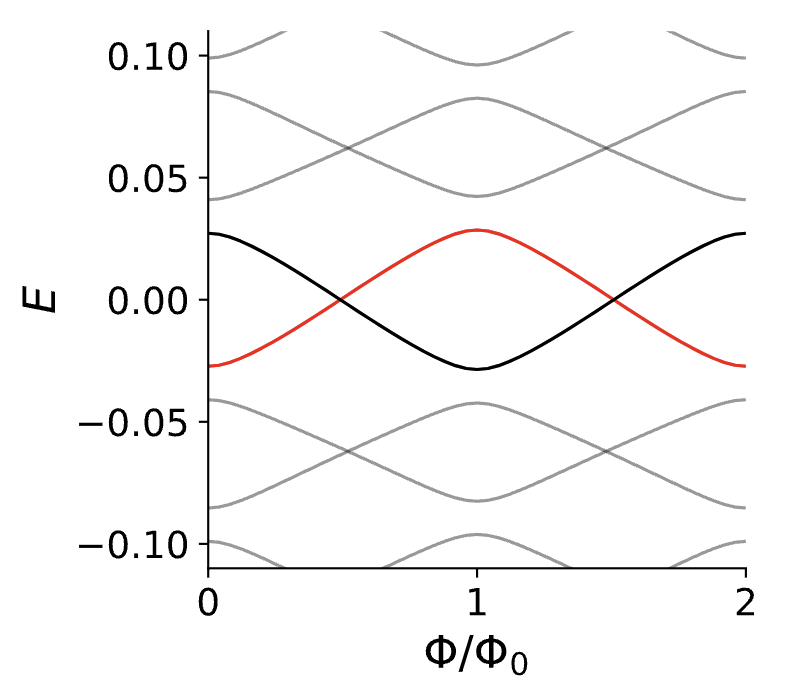
从能谱演化中可以看到，费米子宇称变换的位置的确出现了(能谱交叉)，而且出现在$\Phi=\Phi_0/2$附近，那么可以在超导环中测量这个费米子宇称切换吗？

Detecting the fermion parity switch using the Josephson effect

基态费米子宇称的变化可以用所谓的约瑟夫森效应来检测。约瑟夫森电流可以由能量算符对磁通量的导数的期望值来计算，

\[I(\Phi)=\frac{1}{2}\frac{d E_\textrm{tot}(\Phi)}{d \Phi},\]

其中$E_\textrm{tot}(\Phi)=\langle H_{BdG}(\Phi)\rangle$是BdG哈密顿量$H_{BdG}(\Phi)$对应的系统总能量。

探测基态费米子宇称切换的关键思想是：绝热改变磁通量$\Phi$且不能改变系统的费米子宇称。如果从处于基态的系统出发，把磁通从$\Phi$提高到$\Phi+\Phi_0$，你最终会处于激发态，与此同时费米子的宇称也发生了变化。要回到具有相同费米子宇称的初始基态，需要将$\Phi$变化$2\Phi_0$才可以。

Note that this argument relies on the absence of a reservoir of electrons, such as a metallic lead. In this case, when the two levels cross at zero energy and the ground state fermion parity changes, there is no electron that can enter or leave the system.

费米子宇称的切换，以及环上的费米子宇称守恒，导致能量$E_\textrm{tot}(\Phi)$和相应的(可以测量的)电流在磁通$\Phi$变化的过程中显示$2\Phi_0$的周期性，即在$\phi$中显示$4\pi$的周期性：

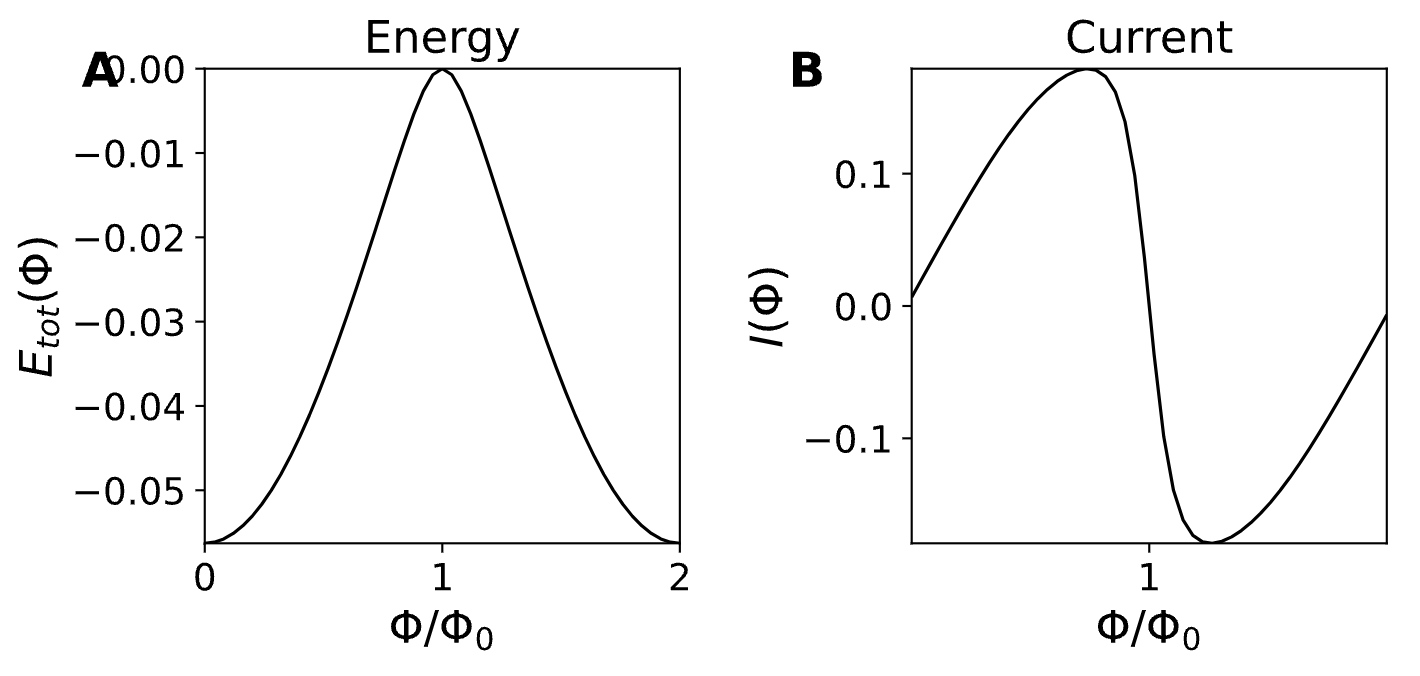
在这一点上，可以问一个问题，约瑟夫森效应的$2\Phi_0$的周期性有什么独特之处？

要回答这个问题，我们需要回顾一种思考约瑟夫森效应的另一种方式，即仅仅通过一个连接点连接一对超导体，而不必将超导体包裹在一个环中。在这种情况下，在与$t e^{i\phi/2}$成比例的隧穿项中出现的跳变相$\phi$(我们也称为超导位相)可以通过将结一侧的费米子算符移一个相即$c^\dagger\rightarrow c^\dagger e^{-i\phi/2}$来消除。对于超导系统，这种变换有一个有趣的效应，即改变结一侧的超导相

\[\Delta\rightarrow \Delta e^{i\phi}.\]

现在你知道为什么$\phi$最初被称为“超导相”了吧。在这个变换(也称为规范变换)之后，$\phi$真正成为与$\Delta$成比例的超导项的复数位相。但这也告诉了我们更多的东西，在规范变换之后哈密顿量$H_{BdG}$只通过电子配对$\Delta e^{i\phi}$依赖于位相$\phi$，所以能量期望值关于$\phi$的周期是$2\pi$。这也就是传统的想法，此时Josephson效应的周期是$2\pi$的。从下面的图中可以看出，这正是在非拓扑相中所发生的情况。在这种情况下，通过能谱的变化发现没有费米子宇称切换出现:

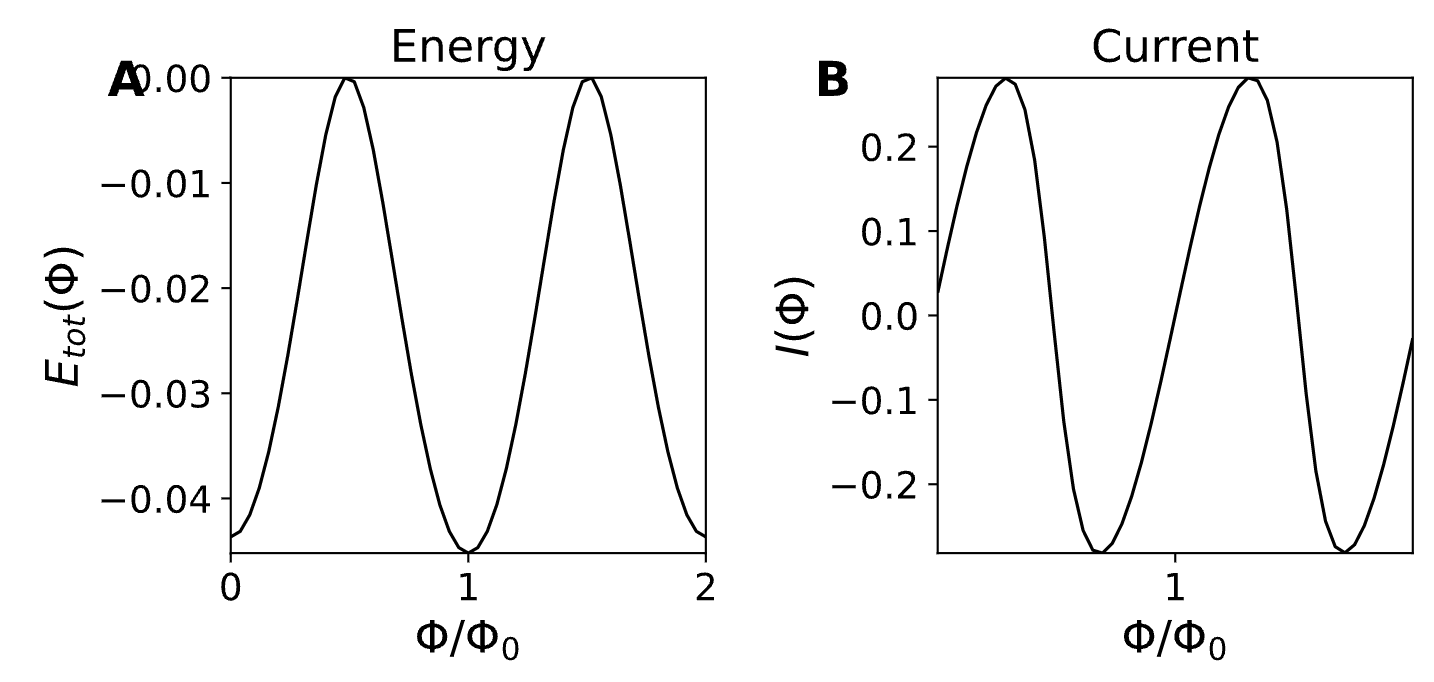
当处于拓扑相的时候，Josephson效应的周期是$4\pi$，因为随着磁通$\phi$的变换，体系能谱发生了交叉，此时系统基态费米子的宇称发生了变化，因此就违反了在普通超导体中Josephson效应是$2\pi$的周期，这种$4\pi$周期的Josephson效应通常也称为$4\pi$(分数)Josephson效应。

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。