最近正好有些空闲的时间，发现自己对拓扑中的一些理解并不深刻，正好借这个机会重新学习一下，加深自己对其中内容的理解，也能让自己之后的研究走的更远。

Hamiltonians with parameters

之前，在研究束缚Majorana链系统的拓扑态时(包括Kitaev链和纳米线)，可以通过研究体哈密顿量$H(k)$计算拓扑性不变量从而表征体系的拓扑性质。关于这个哈密顿量可以有两种视角来理解。首先可以认为它是一个具有动量守恒的无穷系统的哈密顿量

\[H = H(k) \rvert k\rangle\langle k\rvert ,\]

或者可以等效地研究一个只有少量自由度的有限大小系统(对应于单个单元格)，此时它具有一个周期演化的参数$k$。当然，如果不指定$k$是实空间动量，那么在体边对应中就没有任何意义(因为边是实空间中的边)，但拓扑性质仍然可以很好的定义。有时我们想知道如果缓慢改变系统的某些参数，例如偏置电压或磁场，物理系统会发生怎样的变化。因为参数随时间变化，哈密顿量变得随时间变化，即

\[H = H(t).\]

参数的缓慢绝热变化确保了如果系统最初处于基态，它在演化过程中也将保持在基态，因此拓扑性质是有用的。

拓扑要有用的另一个要求是时间演化的”周期性“：

\[H(t) = H(t+T).\]

只有首尾演化是闭合的，参数空间才是闭合的，否则就不能定义拓扑了。周期甚至可以变成$\infty$，在这种情况下$H(-\infty) = H(+\infty)$。要求周期性的原因有些抽象。如果哈密顿量有参数，就研究一个从参数值的空间到所有可能的有能隙哈密顿量的空间的映射。只有当参数值的空间是紧致的，这种映射才具有非平凡的拓扑性质。 对当前考虑的问题来说，这仅仅意味着哈密顿量在时间上必须是周期性的。当然，如果想要有体边对应的系统，那么除了$t$，哈密顿量还必须依赖于实空间坐标，或者动量$k$。

Quantum pumps

在下图中，可以看到一个非常简单的周期时间相关系统，阿基米德螺杆泵

系统的变化显然是周期性的，无论它转动得多慢(也就是改变参数)，泵的工作都是一样的，所以它是一个绝热工具。那么这个泵的量子版本又会如何？这里考虑一个一维区域，在两边连着两个电极，在这个区域施加一个强正弦型的限制电势。当我们移动限制电势时，我们就会拖动其中捕获的电子，系统现在是这样的：

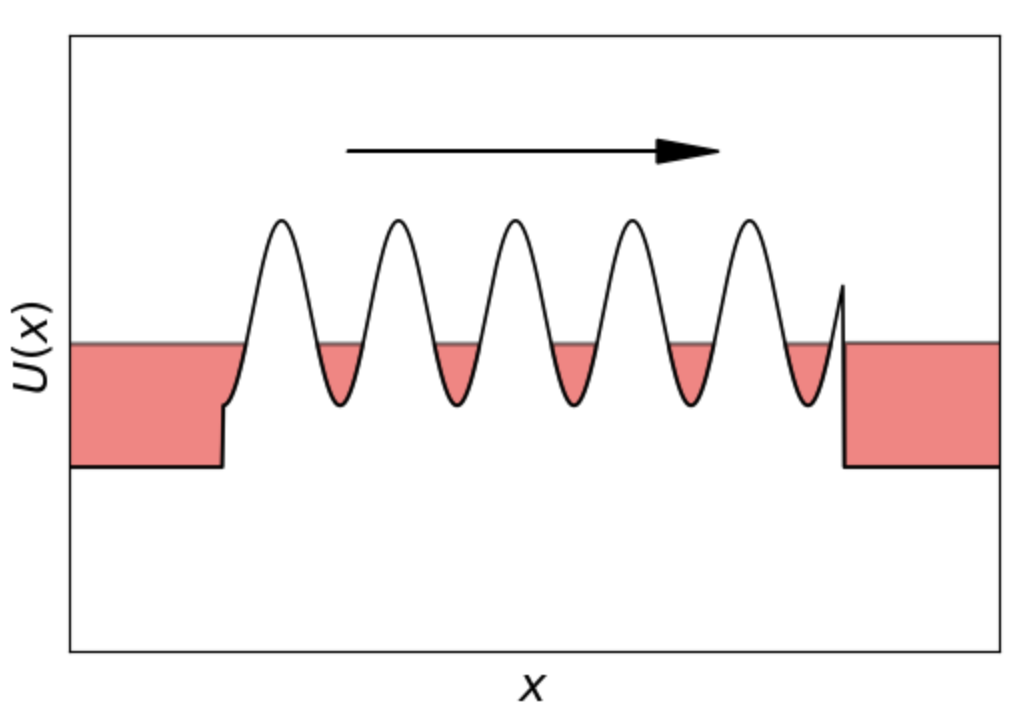
它可以通过哈密顿量描述：

\[H(t) = \frac{k^2}{2m} + A [1 - \cos(x/\lambda + 2\pi t/T)].\]

正如上面讨论的，如果非常缓慢地改变参数$t$，哈密顿量的解将不依赖于$t$变化的速度。当$A \gg 1 /m \lambda^2$时，限制势较强;另外，当化学势$\mu \ll A$时，束缚态在势极小值处的态重叠很小。每个最小值底部附近的势近似是二次的，所以哈密顿量是一个简谐振子的。这就得到了能量为$E_n = (n + \tfrac{1}{2})\omega_c$的分立电子能级，振荡频率为$\omega_c = \sqrt{A/m\lambda^2}$。在大A极限下，不同最小值的状态是完全隔离的，此时能量带是平坦的，传播的消失(群)速度$d E_n(k)/d k=0$。

当增加$A$时，可以数值的检验导线中的连续能带如何变成离散的等间距能带：

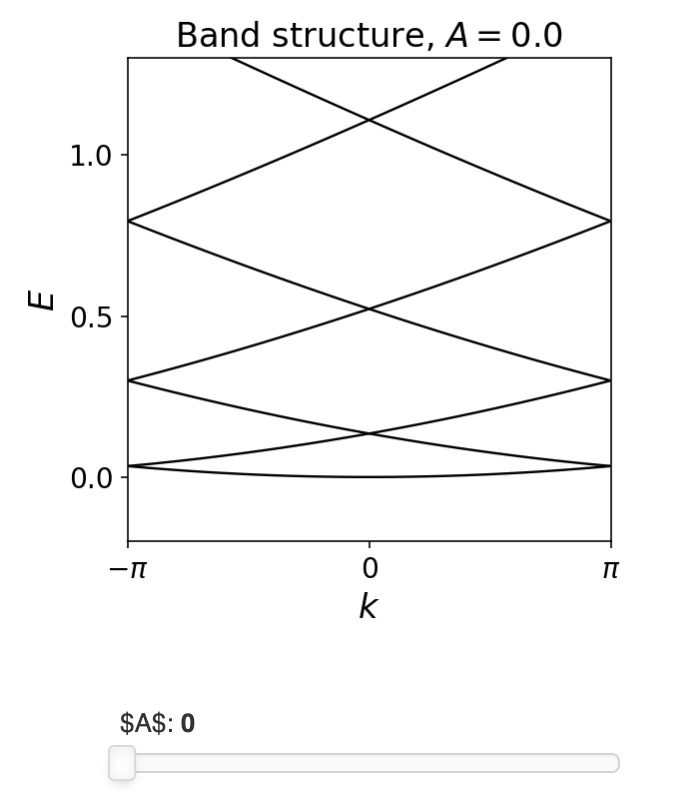
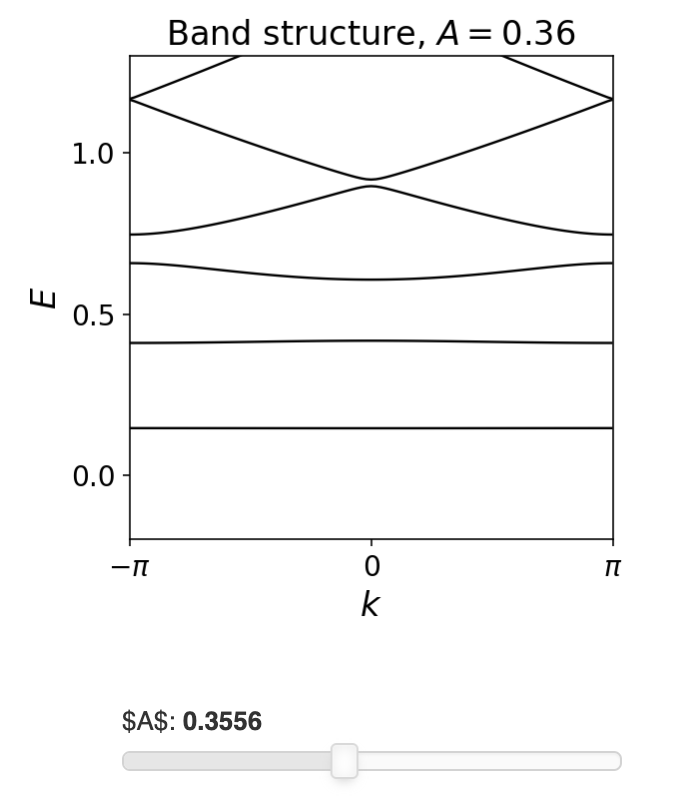
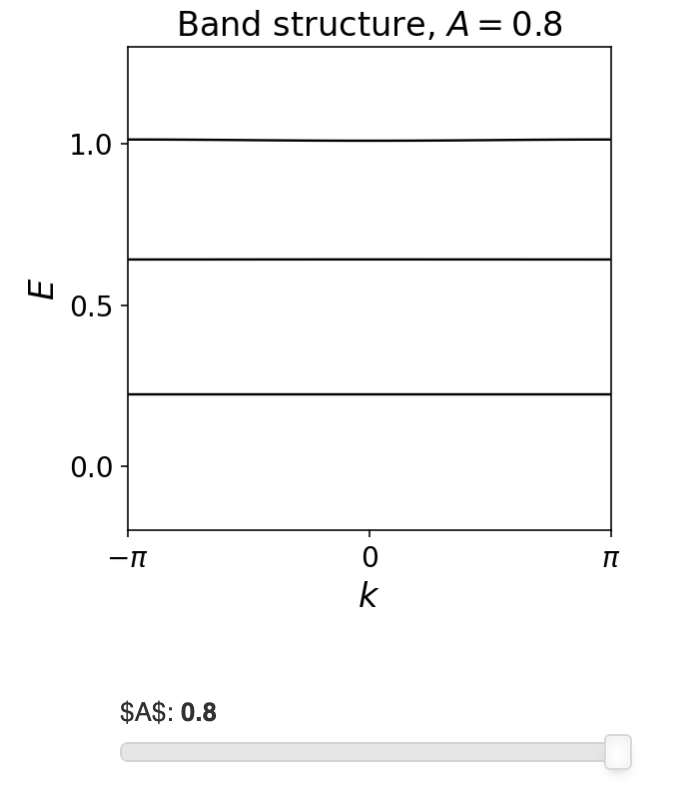
所以除非$\mu = E_n$对于某个$n$，每一个最小电势都包含一个整数电子数$n$。在这个能量下有大量的状态，而在$\mu$与$E_n$之间几乎没有状态。因为电子不会在相邻的势能极值之间移动，所以当改变一个时间区间内的势能极值时，我们正好移动了N个电子。

Quantization of pumped charge

正如前面已经知道的，这个整数很重要，它们可以表明拓扑上发生了什么。在这一点上，我们应该问自己这些问题:每个周期泵送$N$的电子数量的离散性是否受限于电势差的深度，还是说这种离散性是拓扑的一个更普遍的结果？

Thought experiment

这里首先把电极看作是封闭的有限的(但很大的)盒子。当导线中的电势发生变化时，电子明显地从左边的热源移动到右边的热源。电极是如何容纳这些电子的？因为哈密顿量在时间上是周期性的，哈密顿量连同它所有的特征态在周期结束时返回到初始值。绝热定理保证，当哈密顿量缓慢变化时，本征态演化为能量相邻的本征态。

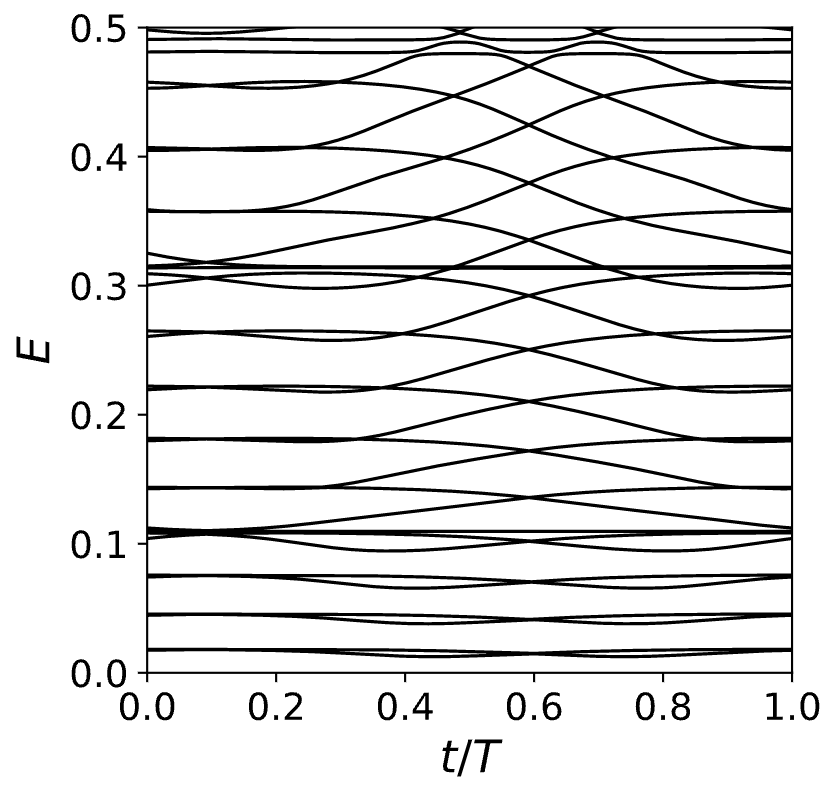
这里确实看到能级在能量上上下移动。能量不变的状态是那些处于周期势最小值的状态。为了更好地理解正在发生的事情，根据质心的位置给每个状态涂上颜色，红色对应左边的热源，蓝色对应右边的热源，白色代表系统的中间

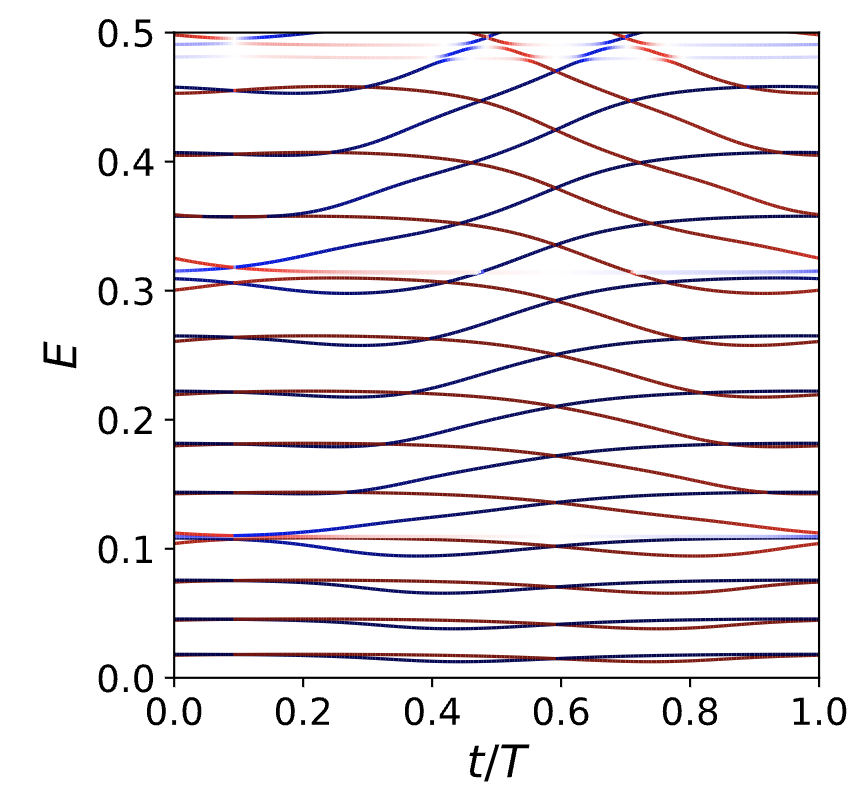
我们看到，在导线能带之间的能隙中的状态属于两个电极中的任何一个。结果发现，位于左侧电极的状态能量下降，而位于右侧电极的状态能量上升(现在这是数字——我们稍后会看到原因)。 可以想象一下，把费米能量(即分离完全被占据态和完全空态的能量)放置在只有很少态的间隙中。随着时间的推移，左库中的空能级从费米能级以上移动到费米能级以下的状态。在这个过程中，由于绝热定理，这种状态的占据不会改变。因此，在泵浦周期结束后，左电极在费米能级以下有一个空态，即少了一个电子。相反的过程发生在右边的引线上，所以它多了一个电子。所以电子在电线中从左边的电极转移到右边，左边能量最高占据态现在占据了右边能量最低的未占据状态。更一般地说，虽然能级不必像图中所示的那样移动，但周期性哈密顿量的能级结构必须回到它自己。左边电极中从费米能级以上到费米能级以下的能级数(可能是负数)必须恰好是左边热源的变化量。这是一个整数。

因此，对“电子从哪里来”的思考使我们得出一个有趣的结论：在绝热泵送循环中泵送的电荷数(与强度$A$无关)是一个整数(可能是$0$)。此外，只要导线在选定的费米能级上有能隙(以便隔离储层)，它就是一个整数。所以不做任何计算，可以得出这样的结论:

The number of electrons pumped per cycle of a quantum pump is an integer as long as the bulk of the pump is gapped. Therefore it is a topological invariant.

Counting electrons through reflection.

泵浦电荷的体哈密顿量$H(k, t)$的表达式是复杂的。它是对$k$和$t$的积分，称为Chern数，或者在其它文献中称为TKNN整数。这里可以使用散射的方法来计算这个数，不过需要从理解电极中的能级如何随时间变化开始。考虑导线中处在能隙中的能级，此时费米能附近的能及被限制在电极中。此时电极中所有的能及都是量子化的，它们都属于驻波，所以它们是向左$\psi_L$和向右$\psi_R$的波的等量叠加，

\[\psi_n = \psi_L(x) + \psi_R(x) \propto \exp(ik_n x) + \exp(-ik_n x + i\phi),\]

波数$k_n$是能量的函数。相对相移$\phi$是满足$x=0$边界条件的必要条件，其中$\psi_L = r \psi_R$，因此$\exp(i \phi) = r$。能级的能量是通过要求$\psi_L$和$\psi_R$的相在$x = -L$时也匹配来确定的。这些边界条件导致了关系

\[2 k_n L = 2n \pi +\phi.\]

按时间$t$连续改变相位$2\pi$使$k_n$从$(2L)^{-1}[2n\pi+ \phi]$变成$(2L)^{-1}[2n\pi+2\pi+\phi]=2k_{n+1}L$。这意味着位相$\phi$的变化导致索引$n$演化为索引$n+1$的状态。因此，相位$\phi$与$2\pi$的winding也改变了波函数$\psi_n \rightarrow \psi_{n+1}$。如前面所讨论的，在电极中这种能级的运动与通过导线在左右电极之间的电荷转移有关。

可以得出结论，如果来自导线的反射相$\phi$增加$2\pi$，这对应于通过导线泵入的单位电荷。

很容易将我们的论证推广到许多模态。为此，只需要对所有反射相移求和，这意味着我们需要查看$\det r$的相位(多个模式的情况下，反射系数是个矩阵形式)。这里得出结论：外部参数的微小变化所泵出的电荷$dq$与反射矩阵$dr$的变化之间存在非常紧密的关系：

\[dq = \frac{d \log \det r}{2\pi i} = \operatorname{Tr}\frac{r^\dagger dr }{ 2 \pi i}.\]

The Hall effect

现在转向量子霍尔效应，它是凝聚态物理中所有拓扑效应之母。首先从经典的霍尔效应开始，这是一个著名的现象，电流垂直于施加的电压流动，反之亦然，电压垂直于流动的电流产生。如何产生霍尔效应？关键是要打破时间反演对称性。流动的电流会破坏时间反演对称性，而电场则不会。因此，任何具有霍尔效应的系统都必须以某种方式打破时间反演对称性。但是等一下，你可能会问，一个与电场平行的正常电流会怎样呢？这是金属中经常发生的事情，金属不会打破时间反演对称性。关键的区别是，这种纵向电流通过能量耗散打破时间反演对称性，能量耗散转化为热量，根据热力学第二定律此时时间反演对称性被破坏。霍尔(Hall)电流的特殊之处在于它是无耗散的。我们可以驱动霍尔电流而不浪费任何能量，因为电流流动垂直于电压梯度方向，因此想要产生Hall电流，必须也要以一种方式破坏时间反演对称性，这里可以通过加入磁场来实现。

How to measure the Hall effect

考虑在二维电子气体中加入垂直的强磁场。取以下几何结构，称为霍尔bar，在实验中经常使用：

如图所示电子气被六个电极接触，可以使用这个霍尔bar的几何设置来测量电子起的传输特性。传输特性用所谓的电导率张量的$\sigma_{xx}、\sigma_{yy}、\sigma_{xy}$和$\sigma_{yx}$四个分量表示。一旦知道了电导率张量，我们就可以用它来计算电流密度$\mathbf{j} = (j_x,j_y)$对金属中电场$\mathbf{E} = (E_x,E_y)$的响应：

\[j_\alpha=\sum_\beta \sigma_{\alpha\beta}E_{\beta}.\]

通过对电流密度与电场之间的这组关系的反演，我们得到了在实验数据中比较常见的电阻率$\rho_{xx}， \rho_{xy}， \dots$。此外，在二维系统中，电导和电导率(或电阻和电阻率)之间没有真正的区别——它们具有相同的物理单位。所以这些项是可以互换的。使用霍尔条器件的方法是沿$x$方向驱动电流$I$，因此有一个电流密度$j_x=(I/W)$，其中$W$是样本的宽度。垂直方向上没有电流密度。

我们可以从电压$V_{1,2,3,4}$的探头之间的电压降使用霍尔bar结构测量电场。然后根据平均方程，从纵向压降$V_L\sim (V_1-V_2)$或$(V_3-V_4)$测量电场的$x$分量

\[E_x \equiv \frac{V_1+V_3-V_2-V_4}{2L}.\]

同样地，我们可以用霍尔电压$V_H=(V_1-V_3)$或$(V_2-V_4)$来测量电场的$y$分量。具体来说，我们可以将电场计算为：

\[E_y \equiv \frac{V_1+V_2-V_4-V_3}{2W}.\]

霍尔bar只能完全测量各向同性或旋转不变系统的电导。如果我们将系统旋转90度，我们可以变换$x\rightarrow y$和$y\rightarrow -x$。因此我们期望纵向电导$\sigma_{xx}=\sigma_{yy}=\sigma_L$。如果我们应用同样的旋转变换，我们得到$\sigma_{xy}=-\sigma_{yx}=\sigma_H$，即霍尔电导。因此，由于转动不变性，4分量的电导张量只有2个独立分量，即纵向和霍尔电导。我们可以用两个电场$E_{x,y}$来计算这些，可以用霍尔bar来测量。为此，我们解$j_y=\sigma_L E_y - \sigma_H E_x=0$和$j_x=\sigma_L E_x+\sigma_H E_y$两组方程，得到$\sigma_{L,H}$。霍尔电导为

\[\sigma_H=\frac{j_x E_y}{E_x^2+E_y^2}.\]

The classical Hall effect is a linear effect

现在尝试着为霍尔bar测量的的霍尔电导$\sigma_H$求得另一种表达式。一般来说，期望霍尔bar中的电场和磁场对电子施加一个力，并增加电子的速度。这里不直接解决这个问题，首先作一个ansatz，电子在外加电场和磁场的时候进入了一种状态，这种状态是由通常的电子基态通过对一个相对于原参考系以速度$\bf{v}$移动的参考系进行伽利略变换得到的。因为在原来的参考系中，电子的平均速度是$\bf v$，所以电子受到的平均力是

\[{\bf F}= e\,(\mathbf{E}+\mathbf{v}\times \mathbf{B}).\]

如果想要一个稳态，那么$\bf F=0$，这意味着${\bf v}= (\mathbf{E}\times \mathbf{B})/B^2$。由于电子以平均速度$\bf v$移动，如果$n$表示电子密度，可以很容易地猜测电流密度为${\bf j}=n e {\bf v}=(n e/ B) (\mathbf{e}\times \mathbf{z})$。结合前面对电流密度的讨论，可以得出这样的结论：简单地根据伽利略不变性，在磁场中的电子气体一定具有的霍尔电导为：

\[\sigma_H=n e B^{-1}.\]

这个关系，即$\sigma_H\propto n$，是非常普遍的，因为它不依赖于电子之间或其他任何东西的相互作用。这被称为Streda关系。如果定义所谓的“填充因子”为$\nu=n h/ e B$，那么霍尔电导可以写成电导量子的倍数$\sigma_H=\nu \frac{e^2}{h}$。

Quantized Hall conductance from pumping: Laughlin argument

为什么量子化霍尔电导$\sigma_H$是如此稳健且不依赖系统细节？显然，这其中一定有一个拓扑的争论。

在实验发现后不久，Laughlin提出了一个极具智慧的论点，将霍尔电导问题映射为拓扑泵浦问题，并在此过程中解释了鲁棒性。下面来讨论一下这个论点。

The Corbino geometry

首先，我们想象在一个被切割成环形的系统中进行霍尔测量，这被称为Corbino盘：

这里还将尝试反向进行实验，即沿圆盘的圆周施加电场，并在径向测量电流$I$，如图所示。径向电流很容易测量，只需测量在Corbino盘的内外边缘之间转移的电荷量$\Delta Q$，就可以得到径向电流$I=\Delta Q/\Delta T$，其中$\Delta T$是这个过程所经过的时间。但是我们如何在切向方向上施加电场呢？最简单的方法是在圆盘的中心施加一个随时间变化的磁场，并利用法拉第效应。

利用法拉第定律$\oint d{\bf{r}\cdot\bf{E}}=\partial_t \Phi$来计算由变化的磁场产生的电场，其中$\Phi$是由圆盘中心的磁场产生的磁通量。假设电场只依赖于半径R，发现得到的切向电场为

\[E(R,t)=\frac{1}{2\pi R}\,\partial_t \Phi.\]

给定$I$，还可以计算测量霍尔电导的另一个分量$\sigma_H$，在相同的半径$R$下径向电流密度$j=I/(2\pi)$。现在知道了沿圆周方向电场又知道了径向电流密度，霍尔电导可以很容易地在这个结构中测量

\[\sigma_H=\frac{j}{E(r,t)}=\frac{I}{\partial_t \Phi}.\]

Laughlin pump

现在准备提出泵浦论证来解释为什么低温霍尔效应是量子化的。为此，我们改变Corbino圆盘中心的磁场，使通量按$\Delta \Phi=\Phi_0=h/e$变化，即一个通量量子随时间$\Delta T$变化。(请注意，这个通量量子只是之前使用的超导通量量子的一半。这是因为现在电流是由电子而不是库珀对携带的。习惯上两者使用相同的符号$\Phi_0$，因为它们经常出现在不同的上下文中)。假设有一个霍尔电导为$\sigma_H$的系统，可以得到转移的电荷为：

\[\Delta Q=I \Delta T=\sigma_H\, \Delta T\, \partial_t\Phi =\sigma_H\,\Delta\Phi=\sigma_H\, \frac{h}{e}.\]

写$\sigma_H=\nu e^2/h$，得到$\Delta Q=\nu e$。由于纵向电导$\sigma_L=0$，可以预期圆盘系统的体态是有能隙的，此时电荷转移$\Delta Q$发生在边缘之间。由于中心的通量$\Phi$是一个通量量子$\Phi_0$，电子的波函数都返回到$\Phi=0$时的波函数。因此，只有整数电荷$\Delta Q=n e$可以在边缘之间泵入。这就是Laughlin关于为什么霍尔电导必须量子化的论点

\[\sigma_{xy}=n e^2/h.\]

在这里，当通量$\Phi$增加$\Phi_0$时，一个整数的电荷从一个边缘泵到另一个边缘。

Landau levels: a microscopic model for the quantum hall effect

一般性的论证目前为止是适用的，因为它适用于任何具有相互作用的复杂电子系统和真实的材料，但如果可以直接计算一些简单系统的霍尔电导，可能感觉会更好。下面试着对磁场中电子的最简单情况做这个。首先，忘记Corbino盘，只在量子力学层面上问电子在磁场中会做什么。

Landau levels on the back of an envelope

我们知道经典电子在垂直磁场中的行为：由于洛伦兹力的作用，它们在回旋轨道上运行。对于速度为v的电子，在强度为B的磁场中，回旋半径为$r_c = mv/eB$。以速度$v$运行回旋轨道的电子，角动量$L=mvr_c=eB ^2_c$。然而，在量子力学中，只有量子化角动量$L=n\hbar$的轨道是被允许的。由$r^2_c = n\hbar/eB$ 得到半径只允许一些离散值$r_n = \sqrt{n} l_B$，其中$l_B = \sqrt{\hbar/eB}$称为磁长。所有的回旋轨道，与半径无关，以相同的频率圆$\omega_c=eB/m$。电子在这个量子化轨道上的能量等于$L\omega_c = n\hbar\omega_c$。所以它的能谱很像谐振子的能谱。通过谐振子$\hbar\omega_c/2$的零点运动，所有的能级也从零能量向上移动。我们最终得到允许能级为

\[E_n = \hbar \omega_c \,\left(n+\tfrac{1}{2}\right)\,.\]

磁场中电子的这些量子化能级被称为朗道能级。 可以在同一个朗道能级中放置许多电子：每一个通过系统的磁通量子对应一个电子。朗道能级简并度很高，与样本的面积成正比。

Landau levels from the Hamiltonian

既然提前知道了答案，就可以解出无应力磁场中电子的Schrödinger方程。更详细地了解量子霍尔效应仍然很重要。系统的哈密顿量为

\[H=(\textbf{p}-e \textbf{ A})^2.\]

向量势$\bf{A}$取决于位置，这使得这个哈密顿量一般来说很复杂。对于均匀磁场，可以通过选择朗道规范来简化计算

\[\textbf{A}(x,y)=\hat{\textbf{x}}B y ,\]

向量势不依赖于x。在这个规范中，整个哈密顿量沿$x$方向是平移不变的，因此与相应的动量$p_x$对易。这允许我们选择$p_x=\hbar k$作为一个好的量子数，此时一个二维哈密顿量可以简化为一维：

\[H(k)=p_y^2+(\hbar k-e B y)^2.\]

除了$y$坐标偏移$y_0(k)=\hbar k/eB$之外，这就是一个简单谐振子的哈密顿量。它的本征值就是朗道能级，它与$k$无关。对应的波函数是沿$y$方向的谐振子波函数和沿$x$方向动量为$k$的平面波函数。在$y$方向上，它们被定位在长度为$\sim l_B$的空间中。这为理解理想二维电子气体的量子化霍尔电导提供了另一种途径。

现在，电子能量以朗道能级量子化，如果在给定的化学势下填充$n$朗道能级，则填充因子为$\nu=n$。然后，Streda公式预测霍尔电导为$\sigma_H=\nu e^2/h=n e^2/h$。纵向导电性必须消失，因为有能隙的系统不允许能量在体中耗散。

Flux pumping of electrons in a Hall cylinder

从朗道能级对电子的微观描述开始，我们现在可以清楚地看到Laughlin泵浦论证是如何工作的。从推导的公式出发，在Corbino几何中这样做有点困难，因为Corbino结构具有旋转对称而不是平移对称。如果我们考虑圆柱体中电子的Laughlin泵浦，这很容易：

事实上，上面画的圆柱体和Corbino圆盘是完全等价的——你可以想象把其中一个变形成另一个。圆柱体的好处是可以保持$(x, y)$的坐标。我们为Laughlin的论点考虑的霍尔圆柱实际上相当于$(x, y)$平面上的一个带，在$x$方向上具有周期边界条件$x\equiv x+L$ ($L$是圆柱的周长)。沿$x$方向的周期边界条件将$k$的允许值离散为$k=2\pi n/L$。

对于Laughlin泵浦理论，我们需要引入一个通过圆柱的通量。利用Stokes定理，我们知道圆柱周围矢量势的线积分一定等于通过它的通量$\oint \textbf{dr}\cdot\textbf{A(r)}=\Phi$。因此，我们可以通过选择矢量势$\bf{A}$引入通量：

\[\textbf{A}(x,y)=(B y +\Phi/L)\,\hat{\textbf{x}}\,,\]

和前面的计算很相似。用$n$标记的状态的哈密顿量为

\[H=p_y^2+\left(\frac{\hbar 2\pi n}{L}-e B y-\frac{e\Phi}{L}\right)^2\,.\]

将上式与量子谐振子进行比较，可以发现谐振子的能级中心必须在

\[y_0(n) = \left(n-\frac{\Phi}{\Phi_0}\right)\frac{h}{e B L}\,.\]

由此可以看出，朗道能级波函数以圆柱轴上$y_0(n)$处的一组离散环为中心，这些环用整数$n$标记。随着$\Phi$的增加，我们看到中心$y_0$移动，因此在一个通量量子$\Delta\Phi=\Phi_0=h/e$之后，所有的电子都沿着$y$向下移动了一步，即$n \rightarrow n-1$。如果$n$朗道能级被填满，那么总电荷$\Delta Q=n e$将在边缘之间转移，这与Laughlin的论证完全一致。

Where do the pumped electrons come from and go to?

通过前面的讨论已经知道，Laughlin的论点解释了霍尔电导的量子化，从一个泵浦的角度来解释，这个泵浦将电子从霍尔圆柱的一端移动到另一端。将这种情况与在之前的课程中学习过的简单电子泵浦进行比较。在那里，泵浦将电子从一个金属铅转移到另一个金属铅上。显然，由于两个金属引线中在费米能级处存在电子态，这个泵浦起了作用。否则，它就没有电子可取，也没有地方可以放电子。没有金属引线，泵浦就像一个空的旋转木马。当应用到霍尔圆柱体上时，通过这个简单的推理表明，Laughlin的论点必然意味着在样品的边缘存在电子态。事实上，我们很容易说服自己这样的状态一定存在。我们只需要再考虑一下经典的电子轨迹，速度为$v$在垂直磁场$B$中运动。这个轨道是一个圆形轨道半径由回旋半径给出。当轨道的中心太接近圆柱体的边缘，比如说比回旋半径更近时，电子的经典轨迹会发生什么变化？画图比说容易：

电子不能离开样品，需要在样品内部反弹。这就形成了所谓的跳过轨道。在真实的样品中，边界上会有一个限制静电势，使电子保持在霍尔条或圆柱体内。体态中的强磁场和边界上的限制势结合在边缘处产生了轨迹，这些轨迹不是闭合的，而是沿着边缘的整个范围移动的。下边界只有向左移动的状态，上边界只有向右移动的状态。在每条边上，只有朝着一个方向运动的状态，而且对对边的方向是相反的。这些在边缘处获得的奇异态通常被称为手性边缘态。边界态的手性是由磁场的方向决定的(平面外vs.平面内)，如果磁场反向，它将在两个边缘反转。上面的漫画是纯粹基于经典物理学的，在给出定量预测之前需要补充量子方面的考虑。后面很快就会看到，上面漫画的量子版本可以给出量子化霍尔效应的解释，补充了Laughlin的论点。但在继续讨论这个问题之前，我们应该意识到上面的漫画实际上是体边界对应的表现形式。如果没有大量的量子霍尔样品，手性边缘态就不可能存在。

A closer look at the chiral edge states

这里更详细地看看霍尔系统的边界。首先考虑一下ribbon结构，我们在讨论霍尔圆筒中的Laughlin泵浦时用到过。这一次，我们将显式地考虑ribbon在$y$方向上具有有限的宽度$W$。在真实情况下，为了将电子限制在这个区域内，必然存在势垒$V(y)$，它必须加到哈密顿量中：

\[H=p_y^2+(\hbar k-e B y-\Phi)^2\,+V(y).\]

这里先来回忆一下，$k=2\pi n/L$因为在$x$上有周期性边界条件。这里并不关心势能的特殊形状。一般来说，它会在ribbon的体态中非常平坦，而在它的边界非常陡峭：

边界势如何影响$H$的能量特征值？在ribbon的体态，远离边缘的位置电势是平坦的，所以可以安全地设置$V(y)=0$。在大部分情况下，仍然得到平坦的朗道水平，能量$E$独立于$k$。这些状态对应于上面所示的经典草图中的回旋轨道。现在靠近边缘。也就是说，让考虑以位置$y_0 = \hbar c k/eB$为中心的状态，该位置距离边缘不超过几个磁长。这些状态对边界限制势非常敏感，因此它们的能量会受到影响。能谱的精确形式不是通用的，它取决于$V(y)$的特定形状。然而，一般来说，期望能量$E(y_0)$相对于原始的朗道能级以与$V(y_0)$成比例的幅度增加。因为$y_0$与$k$成正比，这意味着靠近边缘的状态将依赖于$k$。让我们看看这是否正确，通过为我们的ribbon绘制$E(k)$：

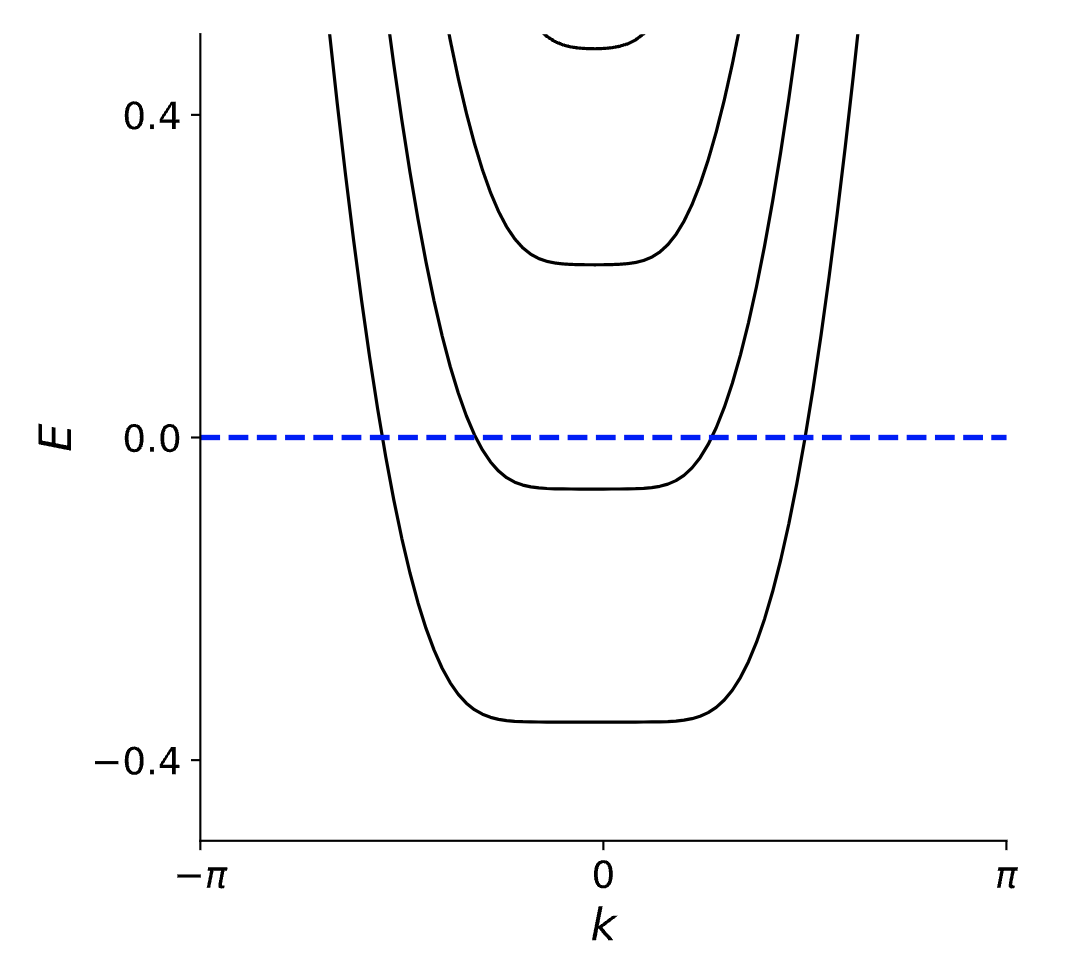
可以看到，由于朗道能级的这种弯曲，即使费米能级像图中那样被放置在一个能隙的中间，也会有穿过它的状态。可以将负$k$的水平与ribbon底部边缘的状态相关联，将正$k$的水平与顶部边缘的状态相关联。对于每条边，在系统的主体中有多少填充的朗道能级，就有多少边界状态。色散$E(k)$的特定形状将取决于边界限制势的细节(在这种情况下是一个无限平方井)。然而，在接近费米能级时，总是可以将边缘态的色散近似为一条直线。然后我们得到，对于每个边缘状态，能量和动量之间的线性关系

\[E = \hbar v (k-k_F).\]

这里的$k_F$是费米动量，在当前能带的情况下费米波矢为$k_F = 2\ π N / L$，其中$N$是系统中的电子数。因为边界势的斜率只是垂直于样品边缘的局部电场$\mathcal{E}_y=-\partial_y V(y)$，所以边缘状态的速度$V$可以简单地解释为跳过状态的漂移速度

\[v = \mathcal{E}_y/B\,.\]

由于限制势产生的局部电场$\mathcal{E}$总是指向样品的内部，所以在两个边缘处速度是相反的。需要注意的一件重要的事情是，边缘状态的存在并不以任何方式依赖于样本的特定形状。可以用任何方式切割量子霍尔系统，但只要它有边，它就会有边界态。为了证明这一点，可以通过绘制霍尔bar中费米能级的局域态密度来绘制边缘态的“图片”

局域态密度完美地揭示了样本中边界态的存在。可以看到，每个填充的朗道能级在状态密度上产生一个最大值，它贯穿整个样本的边缘。在这种情况下，模拟了在体态中有两个填充的朗道能级。

The harmless anomaly of the chiral edges

手性边缘态可以用如此简单的术语来描述，以至于可能会怀疑它们在没有体态的情况下不可能存在。毕竟，难道我们不能仅仅建立一个关于单一手性边缘状态的理论，而忽略量子霍尔系统的整体和另一个边缘的存在吗？一个真正的一维系统就不能表现出与量子霍尔效应的手性边缘状态相同的行为吗？考虑方程$E=\hbar v (k-k_F)$，它描述了这些手性态。可以想象一个恒定的电场$\mathcal{E}$可以沿边缘施加，与动量$k$平行。(在霍尔圆柱体中，可以通过将一个随时间变化的磁通穿过圆柱来实现这一点，正如在前面的部分中看到的那样)。动量$k$根据方程$\hbar \dot{k} = -e\mathcal{E}$变化。经过一段时间$t$后，动量$k$的态能量变为$\hbar v (k - k_F - e\mathcal{E}t/\hbar)$。这种增加对应于费米动量的一个时间依赖性的转移，$k_F\to k_F + e\mathcal{E}t/\hbar$。回想一下，$k_F = 2\pi N/L$，其中$N$是电子数，因此，$k_F$的变化率给出

\[\dot{N} = \mathcal{E}L/\Phi_0,\]

$\Phi_0=h/e$是磁通量量子。由于电子数在变化，电荷是不守恒的。特别是，在$\mathcal{E}L t = \Phi_0$的时间过后，似乎正好有一个电子在边缘不知从哪里冒出来。此时，应该明白发生了什么。这就是Laughlin泵浦所展示的，如果只看一个边缘。一边的电子数量可能会增加，因为电子从另一边被耗尽(这不在我们的“理论”中)，并被泵浦入体态直到它们出现。边缘的这种性质被称为手性反常。手性反常告诉我们，如果没有体态，就无法得到一个一致的手性边缘态的理论，而体态同时保留了电荷。手性边缘状态，或任何其他表现出手性异常的东西，是体边对应的一个例子，因为它们只能出现在二维系统的边缘，而不能孤立地出现。

Pairs of chiral edges in a 1D wire

之前，从量子霍尔效应的现象学描述开始。知道获得量子霍尔态的一种方法是将电子置于外部磁场中。然而，仍然没有一个简单的格哈密顿量来描述量子霍尔效应——我们想要一些像Kitaev链模型这样的东西，它在之前对理解Majorana非常有用。找到这个紧束缚模型的另一个好处是，它不需要外部磁场来展示量子霍尔效应的独特特性。这种模型的确是存在的，它们被称为Chern绝缘体。没有外部磁场的量子霍尔效应也被称为量子反常霍尔效应。Duncan Haldane第一个发明了Chern绝缘体模型，现在被称为Haldane模型。

General strategy to construct a lattice model for the Quantum Hall Effect

这里要做的是按照“多米诺骨牌描述”得到一个Chern绝缘体模型，就像在之前得到Kitaev模型一样。这里的方法将包括两个关键方面：

• 关注量子霍尔边缘的独特性质，它不能独立于体而存在，只能因为体与边界对应而存在。对于Kitaev链，这个性质是存在未配对的Majorana模。在量子霍尔效应中，它是手性边缘态。

• 找到一个更低维度的bulding block，从中可以通过一种聪明的方式“提取”出我们感兴趣的奇异对象。在Kitaev链中，其bulding block就是费米子格点，可以把它们看作是一对Majorana模。

所以需要找到一个一维体系它可以包含一对手性边缘态。由于它们是一维的，这些状态必然在空间上相互叠加，本质上是一对速度相反的传播模式。一旦有了这个building block，我们就可以遵循多米诺方法：将反传播状态成对配对，就像我们对马约拉纳模所做的那样。我们得到了一对空间分离的手性边缘态，从而得到了一个没有磁场的量子Hall绝缘体。所以这里的计划是把左边的系统变成右边的系统：

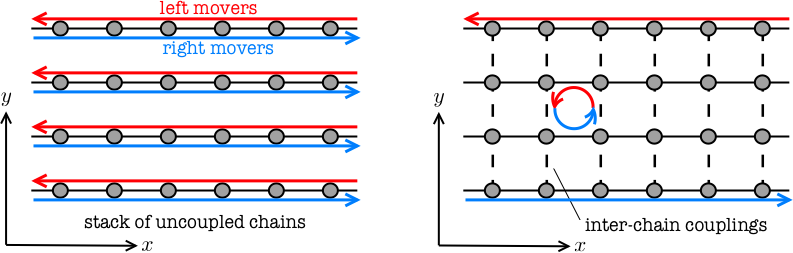
从而就可以用2D的格点模型来描述量子Hall态。

Getting a one dimensional wire with a pair of edge states

首先专注于计划的第一步：找到一个具有一对反传播手性态的一维体系。得到一对相反方向运动的状态的最简单的方法是用一个有效质量的一维单电子哈密顿量。这样的系统具有抛物色散，并且在有限费米波矢量$k=\pm k_F$处的低能激发向相反方向移动。问题是这两种状态有不同的动量，对于一对边缘，处理动量守恒是棘手的(虽然不是不可能的)。所以我们要避免这种方法。之前已经遇到过的模型，Kitaev链在拓扑相变时的狄拉克模型$H= \Delta k \tau_y$。更具体地说，之前把动量空间中的Kitaev哈密顿量写成$H(k)=-(2 t\cos{k}+\mu)\tau_z+\Delta \sin{k}\tau_y$。在临界点$\mu=-2t$处，发现Kitaev哈密顿量变成

\[H=-2t(\cos{k}-1)\,\tau_z+\Delta\sin{k}\,\tau_y.\]

可以看到，在$k\approx0$处，有一对波函数的本征值是$\tau_y$的$\pm 1$，它们的速度相反相等。在这一点上，考虑到Kitaev模型具有超导性，因此$\tau$矩阵指的是粒子和空穴自由度。事实上，这些成分不应该进入量子霍尔效应的描述中。但这不是一个真正的问题，因为这里可以将$\tau$矩阵解释为在左移和右移的空间中操作。根据不同的环境，以不同的方式解释哈密顿项的灵活性，是用toy model思考的优势之一(在不同的地方，可以给Pauli矩阵赋予不同的自由度进行解释)。最后，在继续计划之前，请记住，考虑低维模型的相变点实际上是构建高维拓扑模型的一个相当通用的策略。

QHE without a magnetic field

Deriving the model Hamiltonian

现在把1D的边界态连接起来，构建量子霍尔系统。我们取一堆1D链，都沿着水平方向$x$延伸，如上图所示。沿着$y$的方向把它们一个接一个地堆叠起来，这样就形成了一个正方形晶格。如果有一个足够大的(理想情况下是无限的)链进行堆叠，就可以得到一个真正的二维系统。现在，让先用索引$n_y$标记链，它只能取整数值。同样也替换$k\rightarrow k_x$来表示沿链方向的波矢。因此单独一条链具有哈密顿量

\[[-(2 t\cos(k_x)+\mu)\tau_z+\Delta \sin(k_x)\tau_y]\otimes\rvert n_y\rangle\langle n_y\rvert\]

投影子$\rvert n_y\rangle\langle n_y\rvert $需要从堆叠的链中选出一条链。现在我们要做的就是将一条链的$\tau_y=-1$分支连接到相邻链的$\tau_y=+1$分支上，就得到了一个量子霍尔态。耦合不同链上相反方向移动的边界态的项为

\[\rvert \,n_y\rangle\langle n_y+1\rvert \otimes (\tau_z+i\tau_x)\]

第一部分会耦合相邻的链，而矩阵$(\tau_z+i\tau_x)$则会将向右移动的变成向左移动的，这正是我们想要的。将这种耦合的强度记为$\gamma$。为了得到链的完整哈密顿量我们只需要对$n_y$求和，就得到

\[H=\sum_{n_y}\,\left[-(2 t\cos{k_x}+\mu)\tau_z+\Delta \sin{k_x}\tau_y\right]\,\otimes\,\rvert \,n_y\rangle\langle n_y\rvert \,-\,\gamma\,\sum_{n_y}\,\left[\rvert \,n_y\rangle\langle n_y+1\rvert \otimes (\tau_z+i\tau_x)\,+\,\textrm{h.c.}\right].\]

这个哈密顿量原则上足以产生量子霍尔态。

Gap and edge states

让我们首先考虑一个有限数量的链$n_y=1，\dots,N$。如果将每个链单独调到$\mu = -2t$点，那么很容易验证在$k_x \approx0$处，上面的哈密顿量对于$n_y=1$有一个右移边缘特征态，特征值为$\approx \Delta k_x$，对于$n_y=N$有一个左移边缘特征态，特征值为$\approx -\Delta k_x$。接下来要检查的，这些是否是唯一接近于零能量的本征态。换句话说，系统在二维体中是否有能隙？为了理解这个，首先切换到沿着$y$方向的进行无限堆叠。然后就有了完全平移不变性，所以我们可以在y方向上的动量空间中处理问题。从而可以得到2D的哈密顿量

\[H(k_x,k_y)=[-(2t\cos{k_x}+\mu)\tau_z+\Delta\sin{k_x}\tau_y]-2\gamma\,[\cos{k_y}\tau_z+\sin{k_y}\tau_x].\]

因为这个哈密顿量是三个泡利矩阵的和，能量谱可以写成

\[E(k_x,k_y)=\pm\sqrt{\Delta^2\sin^2{k_x}+(2\gamma\cos{k_y}+\mu+2t\cos{k_x}))^2+4\gamma^2\sin^2{k_y}}.\]

除了特殊的点，这个能谱是有能隙的，正如我们想要的。例如，如果$\mu<-2t-2\gamma$，它就是有能隙的。如果我们从这个点开始，增加$\mu$的值，能隙在$\mu = -2t-2\gamma$处关闭，然后重新打开。

Dirac equation at the phase transition

在相变点附近的两个相很容易理解。一个是具有手性边缘态的量子Hall相，这是我们最初的目标。另外一个是拓扑平庸态。可以通过首先取$\mu$非常正且很大，然后取$\gamma\to 0$来理解这个平庸的相。然后我们就得到了一堆相互之间没有耦合的一维链，它是一个没有边界态的平庸相。在$k_x\approx0$和$k_y\approx0$的相变点附近写下有效哈密顿量是很有用的。它由二维的狄拉克哈密顿量给出：

\[H_{\textrm{Dirac}}=[\Delta k_x\tau_y-2\gamma k_y\tau_x+m\tau_z],\]

系数$m=-(\mu +2t+2\gamma)$在这个狄拉克模型中充当“质量”。如前所述，看到在$m=0$处的无间隙相变点由无质量狄拉克哈密顿量描述的。相变将拓扑相与平庸相分离，质量项在这两个不同的相中是相反的(在这种情况下，拓扑相中的$m>0$和平庸相中的$m<0$)。

与Kitaev链一样，狄拉克模型为我们在拓扑相和平庸相之间的畴壁上构造手性边缘态提供了另一种方法。在研究拓扑Kitaev看到对于一维狄拉克模型，质量$m$中的畴壁上存在非简并零模。固定$k_y=0$，我们看到这里的一维狄拉克哈密顿量与之前看到的相同，其中$m<0$和$m>0$之间的局域畴壁的零模是一个特征态$\tau_x$，特征值$+1$。不像一维的情况，零模在二维的情况下不是静止的。通过添加$2\ k_y\tau_x$作为微扰，可以看到状态的能量为

\[\epsilon(k_y)\approx 2\gamma k_y\,,\]

所以它的速度$v=2\gamma$ ，它的方向取决于$\gamma$的符号。

Dirac cones in graphene

在上面的讨论中，看到了如何通过耦合一维系统来获得量子Hall态。最后，我们的方法是首先得到一个狄拉克锥，在锥上加上一个质量项，最后得到这个质量变化符号。按照这个方法，可以在不施加外部磁场的情况下获得手性边缘态。有一个真实的(也是非常重要的)二维体系，它具有狄拉克锥:石墨烯。在后面的分析中，将把石墨烯当作一个具有手性边缘态的拓扑体系。石墨烯是一层碳原子排列在蜂窝状晶格中。它是一个三角形晶格，每个单元格有两个原子，类型为$A$和类型为$B$，用图中红色和蓝色的点表示：

因此，原胞中的波函数可以写成两个位点上振幅$A$和$B$的向量$(\Psi_A， \Psi_B)^T$。取一个简单的紧束缚模型，其中电子可以以跳跃强度$t$在相邻位点间跳跃，得到布洛赫哈密顿量：

\[H_0(\mathbf{k})= \begin{pmatrix} 0 & h(\mathbf{k}) \\ h^\dagger(\mathbf{k}) & 0 \end{pmatrix}\,,\]

这里$\mathbf{k}=(k_x, k_y)$以及

\[h(\mathbf{k}) = t_1\,\sum_i\,\exp\,\left(i\,\mathbf{k}\cdot\mathbf{a}_i\right)\,.\]

这里$\mathbf{a}_i$是图中的三个向量，连接了晶格的最近位置(将晶格间距设置为1，例如$\mathbf{a}_1=(1,0)$)。引入一组作用于子格自由度的泡利矩阵$\sigma$，我们可以将哈密顿量写成紧凑形式：

\[H_0(\mathbf{k}) = t_1\,\sum_i\,\left[\sigma_x\,\cos(\mathbf{k}\cdot\mathbf{a}_i)-\sigma_y \,\sin(\mathbf{k}\cdot\mathbf{a}_i)\right]\,.\]

能谱$E(\mathbf{k}) = \pm\rvert h(\mathbf{k})\rvert $产生了石墨烯著名的能带结构，两个能带在布里维区的六个角接触：

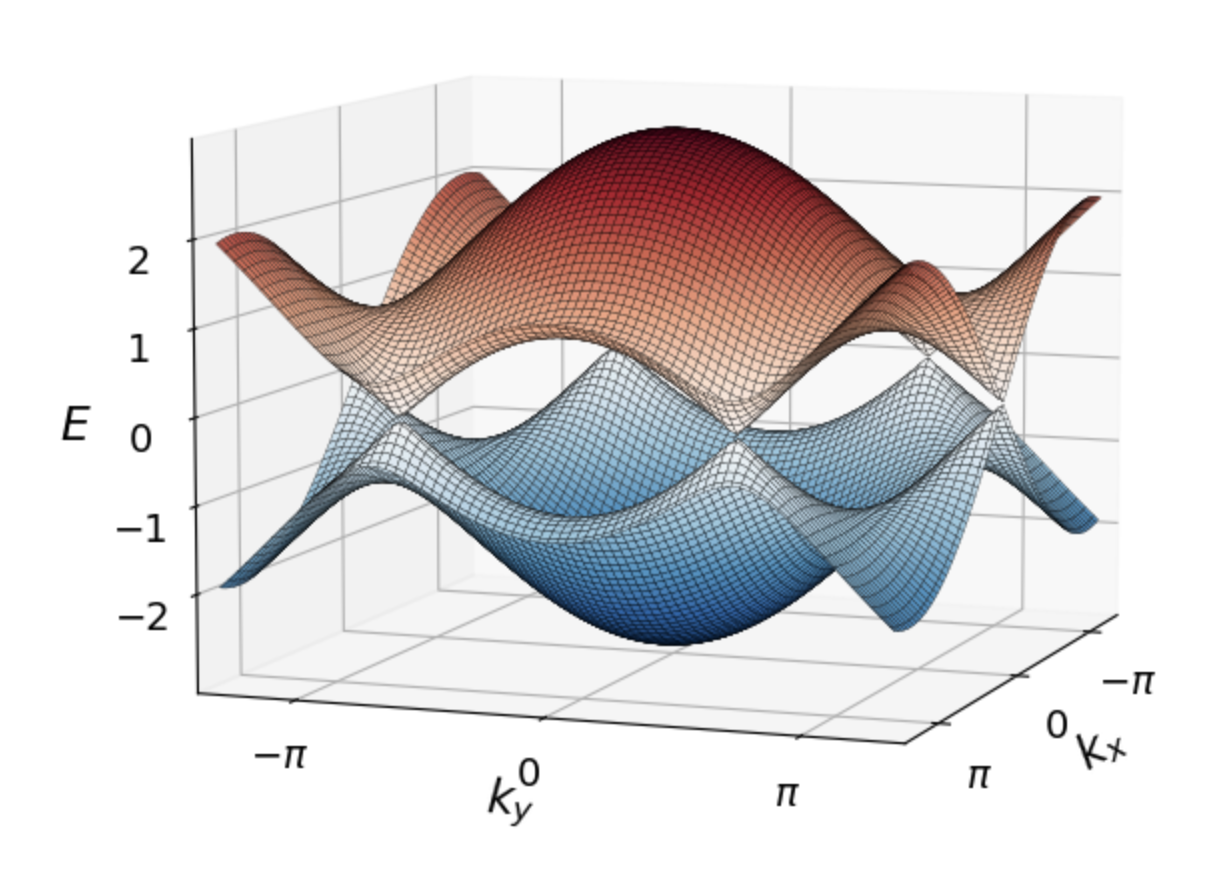
这六个狄拉克视锥中只有两个是真正不同的，分别是$\mathbf{K}=(2\pi/ 3,2 \pi/3\sqrt{3})$和$\mathbf{K}’=(2\pi/3， -2\pi/3\sqrt{3})$。其他的都可以通过在$\mathbf{K}$和$\mathbf{K}’$中加入倒格向量来获得。

Discrete symmetries of graphene

正如之前讨论的，石墨烯是具有子晶格对称性的系统，哈密顿量中仅有两个非对角的子块。子晶格对称性表示为

\[\sigma_z\,H_0(\mathbf{k})\,\sigma_z = -H_0(\mathbf{k})\,.\]

子格对称只是近似的，它是最近邻紧束缚模型的结果。就像就像反演对称性一样，它保护了狄拉克点，只有破坏了子晶格对称性才会打开Dirac锥。除了子晶格和空间反演对称性外，蜂窝晶格在原胞中心周围还具有三重旋转对称性。这种对称性对于狄拉克锥的出现是很重要的。最后，还有时间反演对称性，在紧束缚模型中这个对称性同样存在。由于我们不考虑电子的自旋自由度，实空间中的时间反演对称算符只是复共轭。在动量空间表示中，时间反演操作表示为

\[H_0(\mathbf{k}) = H_0^*(-\mathbf{k})\,.\]

值得注意的是，时间反演对称将$\mathbf{K}$变换到$\mathbf{K}’$，因此它交换了两个狄拉克锥。(近似)子格和时间反演对称操作的乘积产生了另外一个离散对称操作，粒子空穴对称$\sigma_z H^*(-\mathbf{k})\sigma_z = - h_0 (\mathbf{k})$。

Making graphene topological

让回想一下，我们的目标是使石墨烯进入具有手性边缘态的量子霍尔态。第一个必要的步骤是使系统的具有较大的体态能隙。如何打开石墨烯的能隙？狄拉克点同时受到子晶格(反演)和时间反演对称性的保护。因此，可以想到许多方法来打开$\mathbf{K}$和$\mathbf{K}’$的能隙。

First try

打破子格对称性最简单的方法是分别给$A$或$B$分配一个相反的占位能$M$或$-M$。哈密顿量为

\[H_0(\mathbf{k}) + M\,\sigma_z\,.\]

这将会打开能隙

\[E(\mathbf{k})=\pm \sqrt{\rvert h(\mathbf{k})\rvert ^2 + M^2}\,.\]

然而，很快就会发现这样做会陷入一种相当无聊的境地。取极限$\rvert M\rvert \gg t_1$，得到电子态局域在两个子格$A$或$B$中，与$M$的符号无关。最重要的是，并没有出现边界态。很容易看出为什么这个质量项不能产生边界态：它保持了时间反演对称性。在时间反演对称性存在的情况下，绝对不可能获得手性边缘态。

Second try

还有另一种更巧妙的方法，可以将石墨烯中的狄拉克锥分离出来，这也是当前模型的精髓所在。它包括添加假想的第二近邻hopping，具有以下独特的模式：

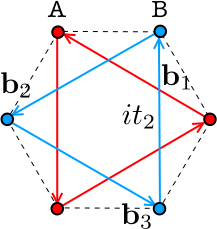
根据箭头的方向，我们表示跳跃的方向为$+it_2$(相反方向为$-it_2$)。注意以下关于这些跳跃的事情：

• 这些hopping都是虚数，而且它们都具有相同的手性，也就是说，如果你的拇指指向屏幕外，它们都遵循你右手的方向。
• 这些hopping都是相同类型原子之间的耦合：$A$和$A$， $B$和$B$。

通过这些特性可以发现，新的hopping既打破了时间反演对称又打破了子晶格对称。现在完整的哈密顿量变成

\[H(\mathbf{k}) = H_0(\mathbf{k})+ M\sigma_z + 2t_2\sum_i\,\sigma_z\,\sin(\mathbf{k}\cdot\mathbf{b}_i)\,.\]

最后一项在时间反演对称下改变符号，打破它。这是Haldane模型的哈密顿量。下面看当这些特殊的第二近邻hopping存在时，系统会发生什么：

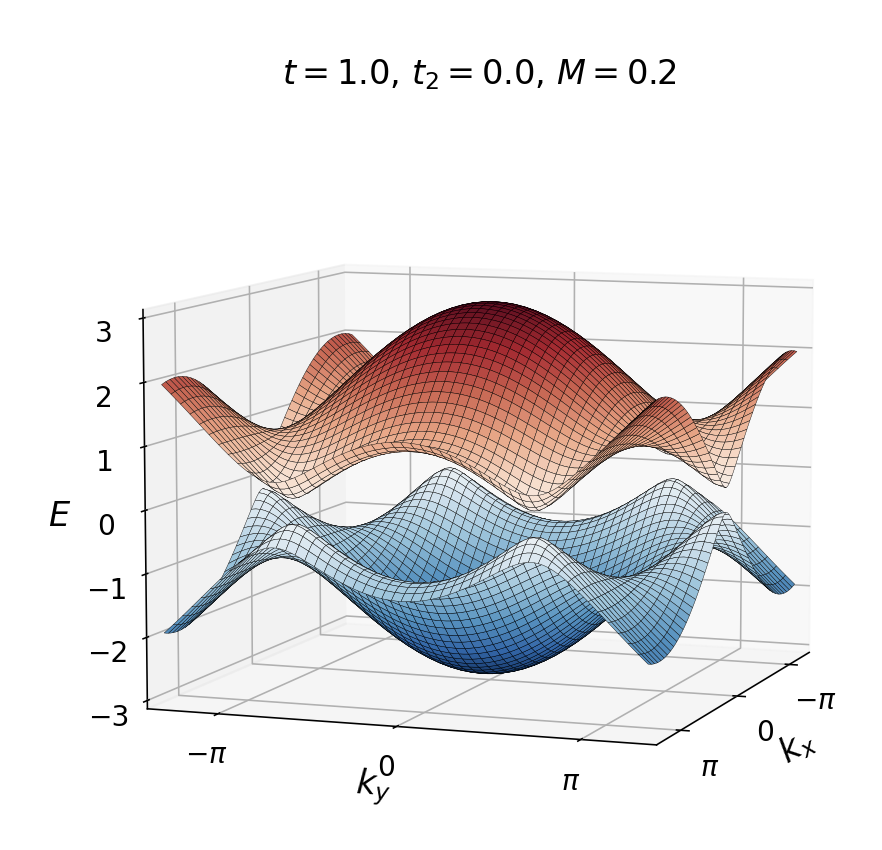
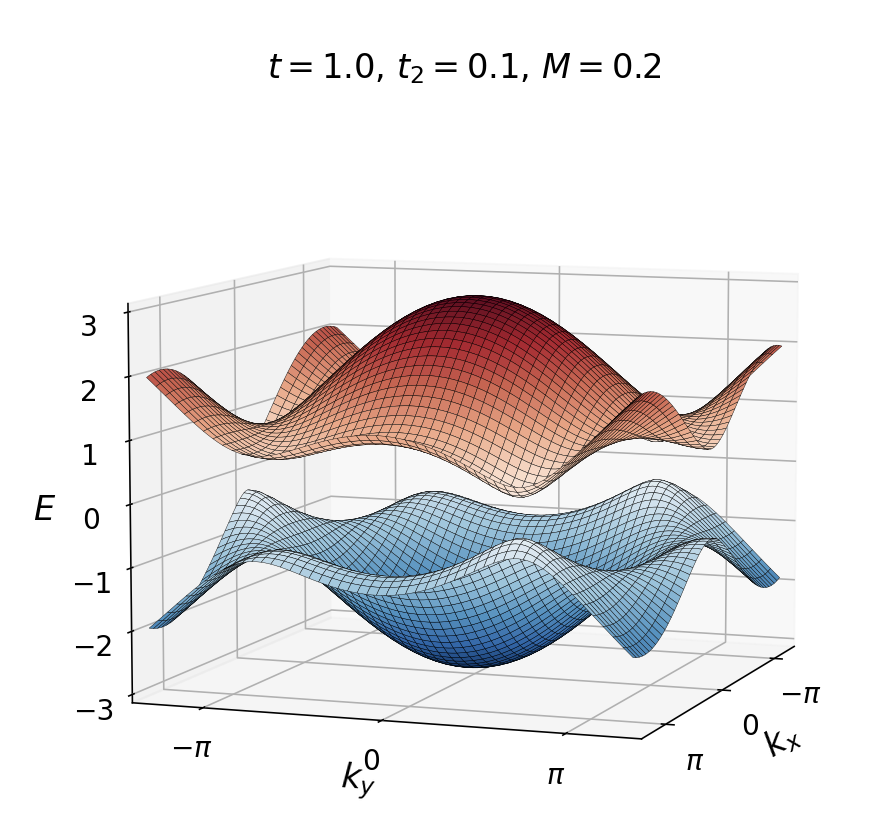
在调节$t_2$过程中会发生能带的闭合再打开过程。当$t_2=0$且在有限的$M$时，系统处于平庸的有能隙相，一般不存在零能态。最初添加一个小的$t_2$并不会改变这种情况，但是当$t_2$经过一个值$\pm M/3\sqrt{3}$时，能隙就会缩小并改变符号。重要的是，只有在两个狄拉克点中的一个点上，差距才会缩小：对于$t_2=M/3\sqrt{3}$，在$\mathbf{K}$;对于$t_2=-M/3\sqrt{3}$，在$\mathbf{K}$。

当发生能隙闭合再打开之后，手性边缘态就出现了。可以通过观察石墨烯带的一维带结构看出这一点。

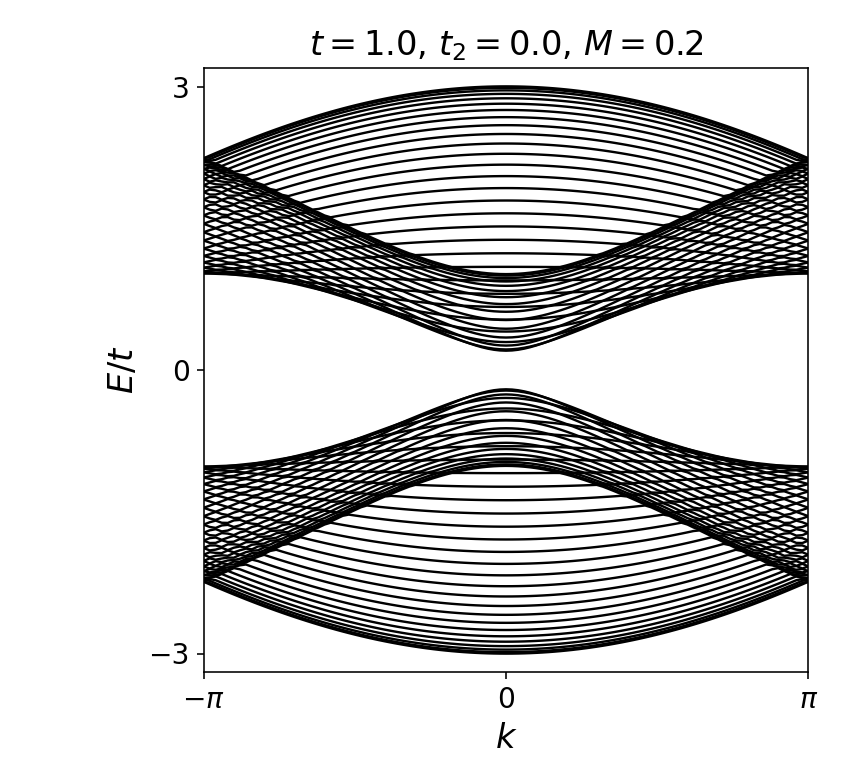
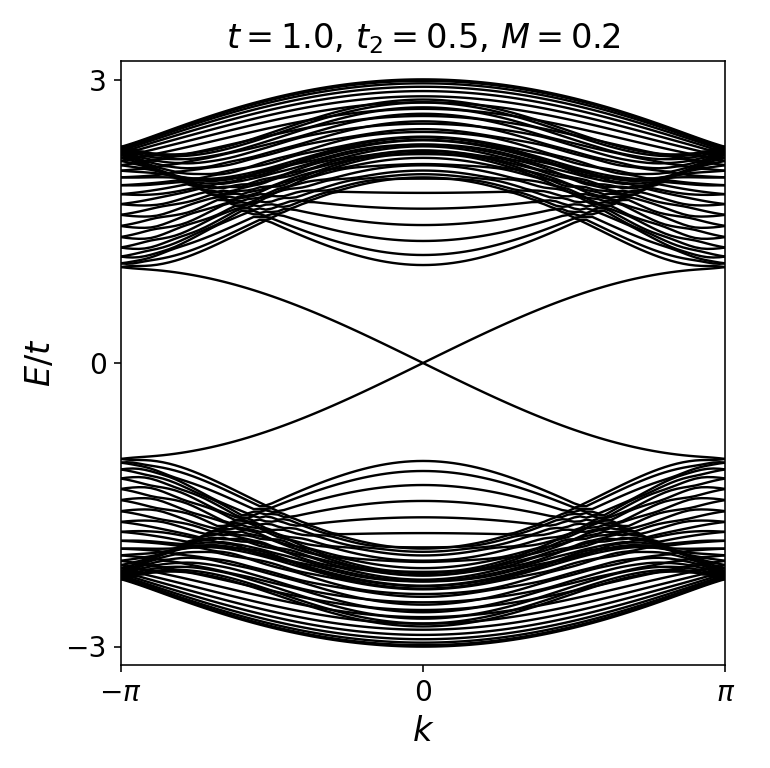
边缘态的出现意味着石墨烯在间隙闭合后进入了拓扑相。这个相类似于量子霍尔相——边缘状态是相同的。然而，它是在没有强磁场的情况下实现的。如你所知，这意味着我们已经创造了一个Chern绝缘体。

Pumping in terms of Berry phase

前面讨论的泵浦抽运论证是把系统放在一个圆柱体上然后绝热泵浦一个磁通量$\Phi$通过圆柱，这样哈密顿量就会回到初始状态。通量通过最小替换进入哈密尔顿量为$H(\mathbf{k})\rightarrow H(\mathbf{k}+e\mathbf{A})$其中${\bf A}=\hat{\mathbf{y}}\Phi/L$。因此，可以从动量变化的角度来理解磁通量泵浦对哈密顿量的影响。当通量的变化是量子的时候，动量$\mathbf{k}$的改变对应一个倒格向量，因此布洛赫哈密顿量返回到它的原始值。为了简化讨论，下面我们将使用正方形布里渊区，$k_x$和$k_y$定义在区间$[0,2 \pi]$中，但这里的所有论点也适用于石墨烯的六边形布里渊区。这里想象这个哈密顿量的本征态$\rvert \psi(\mathbf{k})\rangle$是绝热的随着时间演化，能量为$E(\mathbf{k})$，因为$\mathbf{k}$是缓慢变化的。

假设哈密顿量的本征态$\rvert \psi(\mathbf{k})\rangle$与Haldane模型一样是非简并的。然后，可以通过绝热的移动$\mathbf{k}$研究一条能带，在这个过程中不会遇到能带交叉的情况。经过一段时间，假设时间$T$，在环绕了整个布里渊区之后，让$\mathbf{k}$回到它的初始值。例如，可以考虑以下闭合路径$C$，其中$k_y$在固定的$k_x$下变化$2\pi$，从$k_y=0$开始：

然后可以问：在$T$时刻的最终量子态是什么？很长一段时间以来，人们猜测它只是由初始态$\rvert \psi(k_x, k_y+2\pi)\rangle\equiv\rvert \psi(k_x, k_y)\rangle$乘以通常的相$\exp\left(-i \int_0^T E[\mathbf{k}(T)]d T \right)$给出的，这是哈密顿量的一个特征态随时间累积的结果。这太无聊了。Berry反而意识到，对于闭合循环，有一个额外的相位$\gamma$，在当前的情况下，它可能依赖于$k_x$：

\[\gamma(C) = \oint_C\,\mathbf{A}(\mathbf{k})\,\cdot d\mathbf{k}\,.\]

这里，$\mathbf{A}(\mathbf{k})=i\langle\psi(\mathbf{k}) \rvert \nabla_\mathbf{k}\psi(\mathbf{k})\rangle$是一个有两个复项的向量，它是通过对$\rvert \psi(\mathbf{k})\rangle$对$k_x$和$k_y$求导，然后对$\langle\psi(\mathbf{k})\rvert $求内积得到的。这个向量有个很模糊的名字叫Berry联络。在当前的例子中，周期结束时的最终量子态是这样的

\[\exp\,\left[i\gamma(k_x)\right]\,\exp\,\left(-i \int_0^T E[\mathbf{k}(t)]\,d t\right)\,\rvert \psi(\mathbf{k})\rangle\,.\]

我们已经明确指出，在当前的例子中，$\gamma$可能依赖于$k_x$。这里不会推导Berry位相的公式，这可以直接从Schrödinger方程中得到，例如这里。关于$\gamma$，重要的是要知道它是一个几何相位：它的值取决于路径$C$，而不取决于路径在时间上是如何演化的，因此不取决于$\mathbf{k}(t)$的特定表达式。后面很快就会看到有时它还有更强的拓扑特性。

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。