最近在学习计算超导体系的超流权重,其中要涉及到在确定相互作用$U$下自洽出序参量,虽然之前也会,为了保证所有结果的正确性,这里重新将一些过程记录一下,方便后面查阅理解。
超导序参量自洽


代码
Fortran Version
!==============================================================================================================================================================
! 计算自由电子的超流权重
! H(k) = t(cos kx + cos ky) 正方晶格最近邻
!==============================================================================================================================================================
module code_param
implicit none
integer, parameter :: dp = kind(1.0)
real(dp),parameter::pi = acos(-1.0_dp)
complex(dp),parameter::im = (0.,1.) ! Imagine unit
integer hn,hnn,numk_bz,kn,numk_FS,Un
real(dp) kbt,delta_E,delta_k,engcut,sigma,Umax
real(dp) t1,mu ! 哈密顿量参数
parameter(t1 = 1.0,mu = 1.0)
parameter(hn = 2,hnn = hn/2,kn = 2e2 ,Un = 100,Umax = 1.0,kbt = 1e-5,delta_E = 1e-5,engcut = 100,sigma = 1e-5,delta_k = 1.0/kn) ! hn: 哈密顿量维度
real(dp),allocatable::BZklist(:,:)
end module code_param
!==============================================================================================================================================================
program main
use code_param
use mpi
implicit none
integer numcore,indcore,ierr,nki,nkf
integer i0,i1,i2
real(dp) kx,ky,U0_mpi(Un),U0_list(Un),U0
complex(dp) da_mpi(Un),db_mpi(Un),da_list(Un),db_list(Un)
!-----------------------------------------------------------------------------------------------------------------
!####################################### 并行计算设置 #######################################
call MPI_INIT(ierr) ! 初始化进程
call MPI_COMM_RANK(MPI_COMM_WORLD, indcore, ierr) ! 得到本进程在通信空间中的rank值,即在组中的逻辑编号(该indcore为0到numcore-1间的整数,相当于进程的ID。)
call MPI_COMM_SIZE(MPI_COMM_WORLD, numcore, ierr) !获得进程数量,用numcoer保存
! 并行循环分拆
nki = floor(indcore * (1.0 * Un)/numcore) + 1
nkf = floor((indcore + 1) * (1.0 * Un)/numcore)
!------------------------------------------------------------------------------------------------------------------
! 预设布里渊区撒点
call squareBZ()
!------------------------------------------------------------------------------------------------------------------
if(indcore.eq.0)then
call Fermi_surface()
end if
!------------------------------------------------------------------------------------------------------------------
! 测试超流权重随相互作用U的变化,同时在每个U下面要自洽超导序参量
do i0 = nki,nkf
U0 = Umax/Un * (i0 - 1) ! 改变相互作用强度
U0_mpi(i0) = U0
call gap_equation(U0,da_mpi(i0)) ! 自洽序参量
end do
call MPI_Barrier(MPI_COMM_WORLD,ierr) ! 等所有核心都计算完成r)
call MPI_Reduce(U0_mpi, U0_list, Un, MPI_REAL, MPI_SUM, 0, MPI_COMM_WORLD,ierr)
call MPI_Reduce(da_mpi, da_list, Un, MPI_COMPLEX, MPI_SUM, 0, MPI_COMM_WORLD,ierr)
if(indcore.eq.0)then
! 数据读写
open(32,file = "fortran-order.dat") ! 序参量
do i0 = 1,Un
write(32,"(9F15.8)")U0_list(i0),real(da_list(i0)),aimag(da_list(i0))
enddo
close(32)
endif
call MPI_Finalize(ierr)
stop
end program main
!==============================================================================================================================================================
subroutine gap_equation(U0,delta_A)
! 自洽序参量,然后通过参数返回
use code_param
implicit none
complex(dp) delta_A,delta_B
complex(dp) Ham(hn,hn),matvec(hn,hn),new_deltaA,old_deltaA,new_deltaB,old_deltaB,mat_temp(hn,hn)
real(dp) matval(hn),kx,ky,diff_delta,diff_A,diff_B,ones_mat(hn,hn),U0 ! diff_delta : 控制序参量自洽精度
integer ik0,ie0,ref,matdim
parameter(diff_delta = 1e-5,matdim = hn)
real(dp),external::fermi
! 初猜化学势
old_deltaA = 0.1
diff_A = diff_delta + 1.0 ! 使循环能进入
! 自洽循环
do while (diff_A > diff_delta)
! open(25,file = "self_loop.dat",access = 'append')
! 下面要重新自洽序参量
new_deltaA = 0.0
do ik0 = 1,size(BZklist,2) ! 遍历布里渊区点
kx = BZklist(1,ik0)
ky = BZklist(2,ik0)
call matset_BdG_SC(kx,ky,Ham,old_deltaA)
call diagonalize_Hermitian_matrix(matdim,Ham,matvec,matval)
! Ref: Superconductivity in geometrically and topologically nontrivial lattice models
! 该公式需要 U > 0
ones_mat = 0.0
do ie0 = 1,hn
ones_mat(ie0,ie0) = fermi(matval(ie0))
end do
mat_temp = matmul(matmul(matvec,ones_mat),transpose(conjg(matvec)))
new_deltaA = new_deltaA + mat_temp(1,2)
end do
! 自洽得到新的序参(归一化处理)
new_deltaA = -U0 * new_deltaA * delta_k**2 ! 吸引相互作用才能自洽出超导
! 给定差异来停止自洽过程
diff_A = abs(new_deltaA - old_deltaA)
! 重新赋值继续自洽
old_deltaA = new_deltaA
end do
! 返回自洽收敛后的序参量
delta_A = new_deltaA
return
end subroutine
!==============================================================================================================================================================
subroutine Fermi_surface()
use code_param
integer ikx,iky,ik0,ie
real(dp) kx,ky,mateigval_1(hnn)
complex(dp) Ham_up(hnn,hnn),Ham_down(hnn,hnn),mateigvec(hnn,hnn)
open(31,file = "FS.dat")
do ik0 = 1,numk_bz
kx = BZklist(1,ik0)
ky = BZklist(2,ik0)
call matset_Normal(kx,ky,Ham_up,Ham_down)
call diagonalize_Hermitian_matrix(hnn,Ham_up,mateigvec,mateigval_1)
do ie = 1,hnn
if (abs(mateigval_1(ie)) < 1e-2)then ! 给定能量确定费米面
write(31,"(10F20.8)")kx,ky
end if
end do
end do
close(31)
return
end subroutine
!==============================================================================================================================================================
subroutine matset_BdG_SC(kx, ky, Ham_BdG, delta_A)
! 自由电子气 BdG 哈密顿量
use code_param
implicit none
real(dp), intent(in) :: kx, ky ! 最近邻 & 次近邻矢量
complex(dp), intent(inout) :: Ham_BdG(hn, hn), delta_A
! Initialize Hamiltonian to zero
Ham_BdG = 0.0
! Normal part (particle & hole)
Ham_BdG(1,1) = t1 * (cos(kx) + cos(ky)) - mu ! particle
Ham_BdG(2,2) = -( t1 * (cos(kx) + cos(ky)) - mu) ! hole
! Pairing
Ham_BdG(1,2) = delta_A
Ham_BdG(2,1) = conjg(delta_A)
return
end subroutine matset_BdG_SC
!==============================================================================================================================================================
subroutine matset_Normal(kx,ky,Ham_up,Ham_down)
! 正常态哈密顿量构建
! 矩阵赋值,返回Ham_up & Ham_down
use code_param
implicit none
real(dp) kx,ky
complex(dp) Ham_up(hnn,hnn),Ham_down(hnn,hnn)
!--------------------
! Spin-up
Ham_up = 0.0
! s_0
Ham_up(1,1) = t1 * (cos(kx) + cos(ky)) - mu
!--------------------
!H_{\ua}(k) = H_{\down}(k)
! Spin-down
Ham_down = 0.0
Ham_down = Ham_up
return
end subroutine
!================================================================================================================================================================================================
! function fermi(ek)
! ! 万万不能直接用费米分布函数,会存在浮点溢出
! use code_param,only:dp,kbt
! real(dp) fermi,ek
! fermi = 1.0/(exp(ek/kbt) + 1)
! return
! end
! function fermi(ek)
! ! 万万不能直接用费米分布函数,会存在浮点溢出
! use code_param
! real(dp) fermi,ek
! if(ek/kbt > -engcut .and. ek/kbt < engcut) fermi = 1.0/(exp(ek/kbt) + 1)
! if(ek/kbt < -engcut) fermi = 1.0
! if(ek/kbt > engcut) fermi = 0.0
! return
! end
real(dp) function fermi(ek)
! 零温下的分布函数
use code_param
implicit none
real(dp), intent(in) :: ek
if (ek < 0.0) then
fermi = 1.0
else
fermi = 0.0
end if
end function fermi
!============================================================================================================================
function Gaussian_broadening(energy)
use code_param
implicit none
real(dp), intent(in) :: energy
real(dp) Gaussian_broadening
Gaussian_broadening = exp(-(energy**2) / (2.0 * sigma**2)) / &
(sigma * sqrt(2.0 * pi))
end function Gaussian_broadening
!============================================================================================================================
subroutine squareBZ()
! 构建四方BZ
use code_param
integer ikx,iky,i0
! 对于四方点阵,BZ的点数可以直接确定
numk_bz = (2 * kn)**2
allocate(BZklist(2,numk_bz))
i0 = 0
do ikx = -kn,kn - 1
do iky = -kn,kn - 1
i0 = i0 + 1
BZklist(1,i0) = pi * ikx/(1.0 * kn)
BZklist(2,i0) = pi * iky/(1.0 * kn)
end do
end do
return
end subroutine
!================================================================================================================================================================================================
subroutine diagonalize_Hermitian_matrix(matdim,matin,matout,mateigval)
! 厄米矩阵对角化
! matin 输入矩阵 matout 本征矢量 mateigval 本征值
integer matdim
integer lda0,lwmax0,lwork,lrwork,liwork,info
complex matin(matdim,matdim),matout(matdim,matdim)
real mateigval(matdim)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
!-----------------
lda0 = matdim
lwmax0 = 2 * matdim + matdim**2
allocate(work(lwmax0))
allocate(rwork(1 + 5 * matdim + 2 * matdim**2))
allocate(iwork(3 + 5 * matdim))
matout = matin
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','U',matdim,matout,lda0,mateigval,work,lwork ,rwork,lrwork,iwork,liwork,info)
lwork = min(2 * matdim + matdim**2, int( work( 1 ) ) )
lrwork = min(1 + 5 * matdim + 2 * matdim**2, int( rwork( 1 ) ) )
liwork = min(3 + 5 * matdim, iwork( 1 ) )
call cheevd('V','U',matdim,matout,lda0,mateigval,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file = "mes.dat",status = "unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine diagonalize_Hermitian_matrix
程序运行
mpiifort -mkl square-sc-mpi.f90 -o rpa mpirun -np ${NUM_MPI} ./rpa rm rpa code_param.mod
Julia Version
# 自洽计算配对序参量
# H(k) = t(cos kx + cos ky) 正方晶格最近邻
#-------------------------------------------------------------------------------
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
# 利用Arpack进行稀疏矩阵对角化,因为只在RPA框架中一般只需要矩阵最大或者最小本征值
#-------------------------------------------------------------------------------
@everywhere function matset_SC(kx::Float64,ky::Float64,delta::ComplexF64)
t1::Float64 = 1.0
mu::Float64 = 1.0
Ham = zeros(ComplexF64,2,2)
Ham[1,1] = t1 * (cos(kx) + cos(ky)) - mu
Ham[2,2] = -t1 * (cos(kx) + cos(ky)) + mu
Ham[1,2] = delta
Ham[2,1] = conj(delta)
return Ham
end
#-------------------------------------------------------------------------------
@everywhere function BZpoints(kn::Int64)
knn::Int64 = 2 * kn + 1
klist = zeros(Float64,2,knn^2)
ik0 = 0
for ikx in -kn:kn
for iky in -kn:kn
ik0 += 1
klist[1,ik0] = ikx * pi/kn
klist[2,ik0] = iky * pi/kn
end
end
return klist
end
#-------------------------------------------------------------------------------
# @everywhere function fermi(ek::Float64)
# kbt::Float64 = 1E-10
# return 1.0/(exp(ek/kbt) + 1.0)
# end
@everywhere function fermi(ek::Float64)
if (ek<0)
return 1.0
else
return 0.0
end
end
#-------------------------------------------------------------------------------
@everywhere function self_delta(U0::Float64)
# 自洽计算配对序参量
delta::ComplexF64 = 0.1
delta_new::ComplexF64 = 0.1
diff_delta::Float64 = 0.1
diff_eps::Float64 = 1E-6
hn::Int64 = 2 # 哈密顿量维度
re1 = zeros(Float64,hn,hn)
kn::Int64 = 2E2
dk::Float64 = 1.0/kn
klist = BZpoints(kn) # 布里渊区撒点
while diff_delta > diff_eps
delta_new = 0.0
ik0 = 0
for ikx in -kn:kn
for iky in -kn:kn
ik0 += 1
kx = klist[1,ik0]
ky = klist[2,ik0]
Ham = matset_SC(kx,ky,delta)
val,vec = eigen(Ham)
for ie0 in 1:hn
re1[ie0,ie0] = fermi(real(val[ie0]))
end
temp = vec * re1 * vec'
delta_new += temp[1,2]
end
end
delta_new = -U0 * delta_new * dk^2
diff_delta = abs(delta_new - delta)
delta = delta_new
end
return delta
end
#-------------------------------------------------------------------------------
@everywhere function main()
Un::Int64 = 100
U0list = range(0,1,length = Un + 1)
order = SharedArray(zeros(ComplexF64,Un + 1))
@sync @distributed for iu in 1:Un + 1 # 并行计算
order[iu] = self_delta(U0list[iu])
end
fx1 ="julia-order.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(U0list)
y0 = (a->(@sprintf "%15.8f" a)).(real(order))
z0 = (a->(@sprintf "%15.8f" a)).(imag(order))
writedlm(f1,[x0 y0 z0],"\t")
close(f1)
end
#-------------------------------------------------------------------------------
@time main()
程序执行
julia -p 10 square-sc.jl
Python Version
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#-------------------------------------------------------
t1 = 1.0
mu = 1.0
kn = 100
T = 1E-10
k1 = np.linspace(-np.pi, np.pi, kn)
Klist = np.array([k1, k1])
Umax = 1.0
#-------------------------------------------------------
def SC(kx, ky, delta):
Ham = np.zeros((2, 2))
Ham[0, 0] = t1 * (np.cos(kx) + np.cos(ky)) - mu
Ham[1, 1] = -t1 * (np.cos(kx) + np.cos(ky)) + mu
Ham[0, 1] = delta
Ham[1, 0] = np.conjugate(delta)
return Ham
#-------------------------------------------------------
def fermi(energy):
return 1 / (np.exp(energy / T) + 1)
#-------------------------------------------------------
def diagH(Ham):
eva, evc = np.linalg.eigh(Ham)
return eva, evc
#-------------------------------------------------------
#无法收敛就直接输出-1
def selfC(U, max_iter = 1000):
delta = 1e-4
diff = 1e-6
diff_I = 1.01 * diff
iter_count = 0
while diff_I > diff:
# if iter_count >= max_iter:
# return -1
new_delta = 0
for ik0 in range(kn):
for ik1 in range(kn):
kx = k1[ik0]
ky = k1[ik1]
Ham = SC(kx, ky, delta)
eva, evc = diagH(Ham)
fermi_vals = fermi(eva)
MF = evc @ np.diag(fermi_vals) @ evc.conj().T
new_delta += MF[0, 1]
new_delta = -U * new_delta / kn**2
diff_I = np.abs(new_delta - delta)
delta = new_delta
iter_count += 1
return delta
#-------------------------------------------------------
# selfC(0.5)
U_values = np.linspace(0.0,Umax, 100)
delta_values = []
for U in U_values:
delta_values.append(selfC(U))
plt.figure(figsize=(8, 8))
picname = "order-mu-" + format(mu,".2f") + ".png"
# plt.plot(U_values, delta_values, marker='o', color='b',markersize = 4)
plt.scatter(U_values, delta_values,c = "b", s = 20)
# 设置 x 轴刻度在 1 到 10,步长为 2
# plt.xticks(ticks=range(0, Umax, 2))
# plt.hlines(-0.1,xmin=0,xmax = Umax,colors = "black",lw = 2,ls = "-.")
# plt.vlines(1,ymin=0,ymax=Umax/2.0,colors = "b",lw = 4,ls = "-.")
plt.xlim(0,Umax)
# plt.ylim(-0.1,Umax/2.0)
plt.xlabel(r"$U/t$")
plt.ylabel(r"$\Delta$")
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
plt.title(r"$\mu = $" + format(mu,".2f"))
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
# 减少 x 和 y 轴上的刻度数量
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.grid(True)
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
Python运算速度太慢了,暂时先这样,并行后面再说
结果
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
import matplotlib.gridspec as gridspec
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#----------------------------------------------------------
def plot_fs(mu):
dataname = "FS.dat"
# dataname = "julia-order.dat"
picname = os.path.splitext(dataname)[0] + "-mu-" + format(mu,".2f") + ".png"
da = np.loadtxt(dataname)
plt.figure(figsize=(8, 8))
Umax = np.max(da[:,0])
plt.scatter(da[:,0],da[:,1], s = 20,c = "b")
plt.xlabel(r"$k_x$")
plt.ylabel(r"$k_y$")
plt.title(r"$\mu = $" + format(mu,".2f"))
# plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
#----------------------------------------------------------
def plot_order_compare(mu):
da1 = "fortran-order.dat"
da2 = "julia-order.dat"
picname = "order-compare"
da1 = np.loadtxt(da1)
da2 = np.loadtxt(da2)
plt.figure(figsize=(8, 8))
Umax = np.max(da1[:,0])
plt.scatter(da1[:,0],da1[:,1], s = 20,c = "b",label = "Fortran") # Fortran
plt.scatter(da2[:,0],da2[:,1], s = 20,c = "r",label = "Julia") # Julia
plt.xlabel(r"$U/t$")
plt.ylabel(r"$\Delta$")
plt.title(r"$\mu = $" + format(mu,".2f"))
plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
plt.legend(loc='best', fontsize = 25, scatterpoints = 1, markerscale = 2) # markerscale 调整点的大小
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
#------------------------------------------------------------
if __name__=="__main__":
plot_fs(1.0)
plot_order_compare(1.0)
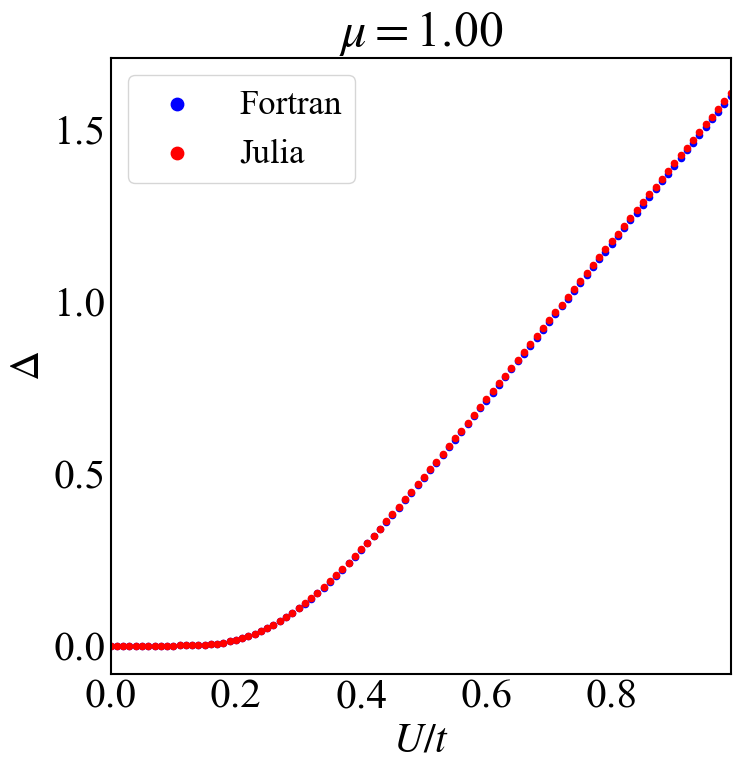
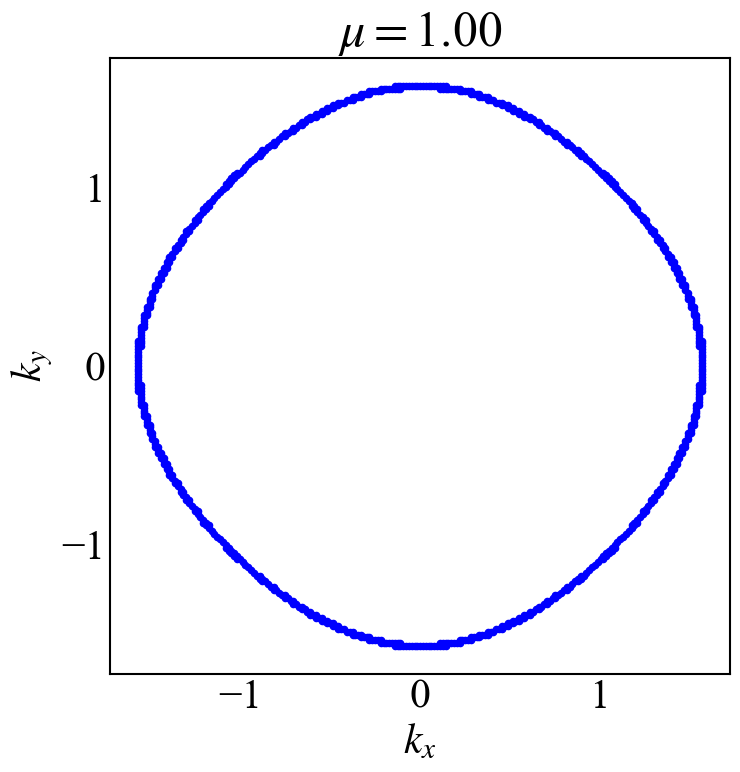
在数值计算对动量分布离散之后,再进行求和的时候需要注意动量间隔$\Delta k_i$具体是多少,这个量如果错了是会影响最后的物理结果的。
变温自洽
- Fortran version
!==============================================================================================================================================================
! 计算自由电子的超流权重
! H(k) = t(cos kx + cos ky) 正方晶格最近邻
!==============================================================================================================================================================
module code_param
implicit none
integer, parameter :: dp = kind(1.0)
real(dp),parameter::pi = acos(-1.0_dp)
complex(dp),parameter::im = (0.,1.) ! Imagine unit
integer hn,hnn,numk_bz,kn,numk_FS,Un
real(dp) kbt,delta_E,delta_k,engcut,sigma,Umax
real(dp) t1,mu ! 哈密顿量参数
parameter(t1 = 1.0,mu = 1.0)
parameter(hn = 2,hnn = hn/2,kn = 1e2 ,Un = 100,Umax = 1.0,delta_E = 1e-5,engcut = 100,sigma = 1e-5,delta_k = 1.0/kn) ! hn: 哈密顿量维度
real(dp),allocatable::BZklist(:,:)
end module code_param
!==============================================================================================================================================================
program main
use code_param
use mpi
implicit none
integer numcore,indcore,ierr,nki,nkf
integer i0,i1,i2
real(dp) kx,ky,U0_mpi(Un),U0_list(Un),U0
complex(dp) da_mpi(Un),db_mpi(Un),da_list(Un),db_list(Un)
!-----------------------------------------------------------------------------------------------------------------
!####################################### 并行计算设置 #######################################
call MPI_INIT(ierr) ! 初始化进程
call MPI_COMM_RANK(MPI_COMM_WORLD, indcore, ierr) ! 得到本进程在通信空间中的rank值,即在组中的逻辑编号(该indcore为0到numcore-1间的整数,相当于进程的ID。)
call MPI_COMM_SIZE(MPI_COMM_WORLD, numcore, ierr) !获得进程数量,用numcoer保存
! 并行循环分拆
nki = floor(indcore * (1.0 * Un)/numcore) + 1
nkf = floor((indcore + 1) * (1.0 * Un)/numcore)
!------------------------------------------------------------------------------------------------------------------
! 预设布里渊区撒点
call squareBZ()
!------------------------------------------------------------------------------------------------------------------
if(indcore.eq.0)then
call Fermi_surface()
end if
!------------------------------------------------------------------------------------------------------------------
! 测试超流权重随相互作用U的变化,同时在每个U下面要自洽超导序参量
do i0 = nki,nkf
kbt = 1.0/Un * i0
! U0 = Umax/Un * (i0 - 1) ! 改变相互作用强度
U0_mpi(i0) = kbt ! 改变系统温度
U0 = 1.0
call gap_equation(U0,da_mpi(i0)) ! 自洽序参量
end do
call MPI_Barrier(MPI_COMM_WORLD,ierr) ! 等所有核心都计算完成r)
call MPI_Reduce(U0_mpi, U0_list, Un, MPI_REAL, MPI_SUM, 0, MPI_COMM_WORLD,ierr)
call MPI_Reduce(da_mpi, da_list, Un, MPI_COMPLEX, MPI_SUM, 0, MPI_COMM_WORLD,ierr)
if(indcore.eq.0)then
! 数据读写
open(32,file = "fortran-order.dat") ! 序参量
do i0 = 1,Un
write(32,"(9F15.8)")U0_list(i0),real(da_list(i0)),aimag(da_list(i0))
enddo
close(32)
endif
call MPI_Finalize(ierr)
stop
end program main
!==============================================================================================================================================================
subroutine gap_equation(U0,delta_A)
! 自洽序参量,然后通过参数返回
use code_param
implicit none
complex(dp) delta_A,delta_B
complex(dp) Ham(hn,hn),matvec(hn,hn),new_deltaA,old_deltaA,new_deltaB,old_deltaB,mat_temp(hn,hn)
real(dp) matval(hn),kx,ky,diff_delta,diff_A,diff_B,ones_mat(hn,hn),U0 ! diff_delta : 控制序参量自洽精度
integer ik0,ie0,ref,matdim
parameter(diff_delta = 1e-5,matdim = hn)
real(dp),external::fermi
! 初猜化学势
old_deltaA = 0.1
diff_A = diff_delta + 1.0 ! 使循环能进入
! 自洽循环
do while (diff_A > diff_delta)
! open(25,file = "self_loop.dat",access = 'append')
! 下面要重新自洽序参量
new_deltaA = 0.0
do ik0 = 1,size(BZklist,2) ! 遍历布里渊区点
kx = BZklist(1,ik0)
ky = BZklist(2,ik0)
call matset_BdG_SC(kx,ky,Ham,old_deltaA)
call diagonalize_Hermitian_matrix(matdim,Ham,matvec,matval)
! Ref: Superconductivity in geometrically and topologically nontrivial lattice models
! 该公式需要 U > 0
ones_mat = 0.0
do ie0 = 1,hn
ones_mat(ie0,ie0) = fermi(matval(ie0))
end do
mat_temp = matmul(matmul(matvec,ones_mat),transpose(conjg(matvec)))
new_deltaA = new_deltaA + mat_temp(1,2)
end do
! 自洽得到新的序参(归一化处理)
new_deltaA = -U0 * new_deltaA * delta_k**2 ! 吸引相互作用才能自洽出超导
! 给定差异来停止自洽过程
diff_A = abs(new_deltaA - old_deltaA)
! 重新赋值继续自洽
old_deltaA = new_deltaA
end do
! 返回自洽收敛后的序参量
delta_A = new_deltaA
return
end subroutine
!==============================================================================================================================================================
subroutine Fermi_surface()
use code_param
integer ikx,iky,ik0,ie
real(dp) kx,ky,mateigval_1(hnn)
complex(dp) Ham_up(hnn,hnn),Ham_down(hnn,hnn),mateigvec(hnn,hnn)
open(31,file = "FS.dat")
do ik0 = 1,numk_bz
kx = BZklist(1,ik0)
ky = BZklist(2,ik0)
call matset_Normal(kx,ky,Ham_up,Ham_down)
call diagonalize_Hermitian_matrix(hnn,Ham_up,mateigvec,mateigval_1)
do ie = 1,hnn
if (abs(mateigval_1(ie)) < 1e-2)then ! 给定能量确定费米面
write(31,"(10F20.8)")kx,ky
end if
end do
end do
close(31)
return
end subroutine
!==============================================================================================================================================================
subroutine matset_BdG_SC(kx, ky, Ham_BdG, delta_A)
! 自由电子气 BdG 哈密顿量
use code_param
implicit none
real(dp), intent(in) :: kx, ky ! 最近邻 & 次近邻矢量
complex(dp), intent(inout) :: Ham_BdG(hn, hn), delta_A
! Initialize Hamiltonian to zero
Ham_BdG = 0.0
! Normal part (particle & hole)
Ham_BdG(1,1) = t1 * (cos(kx) + cos(ky)) - mu ! particle
Ham_BdG(2,2) = -( t1 * (cos(kx) + cos(ky)) - mu) ! hole
! Pairing
Ham_BdG(1,2) = delta_A
Ham_BdG(2,1) = conjg(delta_A)
return
end subroutine matset_BdG_SC
!==============================================================================================================================================================
subroutine matset_Normal(kx,ky,Ham_up,Ham_down)
! 正常态哈密顿量构建
! 矩阵赋值,返回Ham_up & Ham_down
use code_param
implicit none
real(dp) kx,ky
complex(dp) Ham_up(hnn,hnn),Ham_down(hnn,hnn)
!--------------------
! Spin-up
Ham_up = 0.0
! s_0
Ham_up(1,1) = t1 * (cos(kx) + cos(ky)) - mu
!--------------------
!H_{\ua}(k) = H_{\down}(k)
! Spin-down
Ham_down = 0.0
Ham_down = Ham_up
return
end subroutine
!================================================================================================================================================================================================
! function fermi(ek)
! ! 万万不能直接用费米分布函数,会存在浮点溢出
! use code_param,only:dp,kbt
! real(dp) fermi,ek
! fermi = 1.0/(exp(ek/kbt) + 1)
! return
! end
function fermi(ek)
! 万万不能直接用费米分布函数,会存在浮点溢出
use code_param
real(dp) fermi,ek
if(ek/kbt > -engcut .and. ek/kbt < engcut) fermi = 1.0/(exp(ek/kbt) + 1)
if(ek/kbt < -engcut) fermi = 1.0
if(ek/kbt > engcut) fermi = 0.0
return
end
! real(dp) function fermi(ek)
! ! 零温下的分布函数
! use code_param
! implicit none
! real(dp), intent(in) :: ek
! if (ek < 0.0) then
! fermi = 1.0
! else
! fermi = 0.0
! end if
! end function fermi
!============================================================================================================================
function Gaussian_broadening(energy)
use code_param
implicit none
real(dp), intent(in) :: energy
real(dp) Gaussian_broadening
Gaussian_broadening = exp(-(energy**2) / (2.0 * sigma**2)) / &
(sigma * sqrt(2.0 * pi))
end function Gaussian_broadening
!============================================================================================================================
subroutine squareBZ()
! 构建四方BZ
use code_param
integer ikx,iky,i0
! 对于四方点阵,BZ的点数可以直接确定
numk_bz = (2 * kn)**2
allocate(BZklist(2,numk_bz))
i0 = 0
do ikx = -kn,kn - 1
do iky = -kn,kn - 1
i0 = i0 + 1
BZklist(1,i0) = pi * ikx/(1.0 * kn)
BZklist(2,i0) = pi * iky/(1.0 * kn)
end do
end do
return
end subroutine
!================================================================================================================================================================================================
subroutine diagonalize_Hermitian_matrix(matdim,matin,matout,mateigval)
! 厄米矩阵对角化
! matin 输入矩阵 matout 本征矢量 mateigval 本征值
integer matdim
integer lda0,lwmax0,lwork,lrwork,liwork,info
complex matin(matdim,matdim),matout(matdim,matdim)
real mateigval(matdim)
complex,allocatable::work(:)
real,allocatable::rwork(:)
integer,allocatable::iwork(:)
!-----------------
lda0 = matdim
lwmax0 = 2 * matdim + matdim**2
allocate(work(lwmax0))
allocate(rwork(1 + 5 * matdim + 2 * matdim**2))
allocate(iwork(3 + 5 * matdim))
matout = matin
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','U',matdim,matout,lda0,mateigval,work,lwork ,rwork,lrwork,iwork,liwork,info)
lwork = min(2 * matdim + matdim**2, int( work( 1 ) ) )
lrwork = min(1 + 5 * matdim + 2 * matdim**2, int( rwork( 1 ) ) )
liwork = min(3 + 5 * matdim, iwork( 1 ) )
call cheevd('V','U',matdim,matout,lda0,mateigval,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file = "mes.dat",status = "unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine diagonalize_Hermitian_matrix
- Julia Version
# 自洽计算配对序参量
# H(k) = t(cos kx + cos ky) 正方晶格最近邻
#-------------------------------------------------------------------------------
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
# 利用Arpack进行稀疏矩阵对角化,因为只在RPA框架中一般只需要矩阵最大或者最小本征值
#-------------------------------------------------------------------------------
@everywhere function matset_SC(kx::Float64,ky::Float64,delta::ComplexF64)
t1::Float64 = 1.0
mu::Float64 = 1.0
Ham = zeros(ComplexF64,2,2)
Ham[1,1] = t1 * (cos(kx) + cos(ky)) - mu
Ham[2,2] = -t1 * (cos(kx) + cos(ky)) + mu
Ham[1,2] = delta
Ham[2,1] = conj(delta)
return Ham
end
#-------------------------------------------------------------------------------
@everywhere function BZpoints(kn::Int64)
knn::Int64 = 2 * kn + 1
klist = zeros(Float64,2,knn^2)
ik0 = 0
for ikx in -kn:kn
for iky in -kn:kn
ik0 += 1
klist[1,ik0] = ikx * pi/kn
klist[2,ik0] = iky * pi/kn
end
end
return klist
end
#-------------------------------------------------------------------------------
@everywhere function fermi(kbt::Float64,ek::Float64)
# kbt::Float64 = 1E-10
return 1.0/(exp(ek/kbt) + 1.0)
end
# @everywhere function fermi(ek::Float64)
# if (ek<0)
# return 1.0
# else
# return 0.0
# end
# end
#-------------------------------------------------------------------------------
@everywhere function self_delta(kbt::Float64,U0::Float64)
# 自洽计算配对序参量
delta::ComplexF64 = 0.1
delta_new::ComplexF64 = 0.1
diff_delta::Float64 = 0.1
diff_eps::Float64 = 1E-6
hn::Int64 = 2 # 哈密顿量维度
re1 = zeros(Float64,hn,hn)
kn::Int64 = 1E2
dk::Float64 = 1.0/kn
klist = BZpoints(kn) # 布里渊区撒点
while diff_delta > diff_eps
delta_new = 0.0
ik0 = 0
for ikx in -kn:kn
for iky in -kn:kn
ik0 += 1
kx = klist[1,ik0]
ky = klist[2,ik0]
Ham = matset_SC(kx,ky,delta)
val,vec = eigen(Ham)
for ie0 in 1:hn
re1[ie0,ie0] = fermi(kbt,real(val[ie0]))
end
temp = vec * re1 * vec'
delta_new += temp[1,2]
end
end
delta_new = -U0 * delta_new * dk^2
diff_delta = abs(delta_new - delta)
delta = delta_new
end
return delta
end
#-------------------------------------------------------------------------------
@everywhere function main()
Un::Int64 = 100
U0list = range(0,1,length = Un + 1)
kbtlist = range(0,1,length = Un + 1)
order = SharedArray(zeros(ComplexF64,Un + 1))
# @sync @distributed for iu in 1:Un + 1 # For interaction strength
@sync @distributed for iu in 1:Un + 1 # For interaction strength
order[iu] = self_delta(kbtlist[iu],1.0)
end
fx1 ="julia-order.dat"
f1 = open(fx1,"w")
# x0 = (a->(@sprintf "%15.8f" a)).(U0list)
x0 = (a->(@sprintf "%15.8f" a)).(kbtlist)
y0 = (a->(@sprintf "%15.8f" a)).(real(order))
z0 = (a->(@sprintf "%15.8f" a)).(imag(order))
writedlm(f1,[x0 y0 z0],"\t")
close(f1)
end
#-------------------------------------------------------------------------------
@time main()
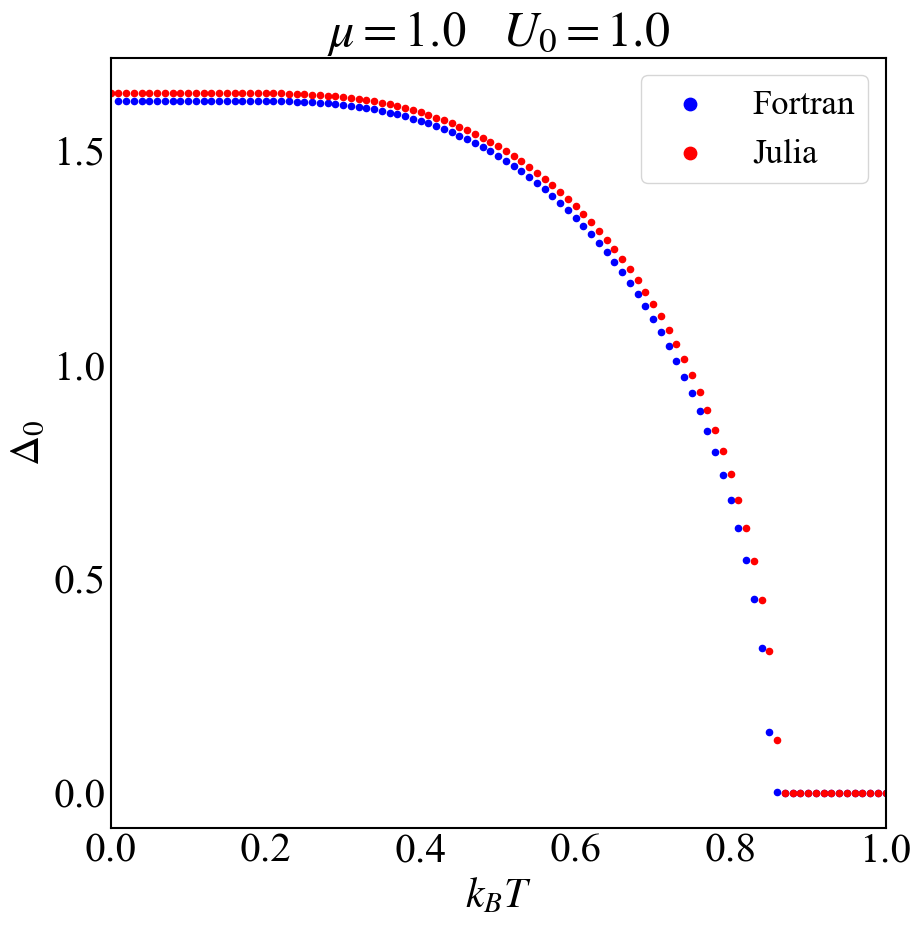
这里因为用Julia和Fortran计算的时候费米分布实际上取的有一点不一样,所以结果略微有一些差异。而且Julia的运行速度是比Fortran要慢的。
- 绘图程序
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
import matplotlib.gridspec as gridspec
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#----------------------------------------------------------
def plot_fs(mu):
dataname = "FS.dat"
# dataname = "julia-order.dat"
picname = os.path.splitext(dataname)[0] + "-mu-" + format(mu,".2f") + ".png"
da = np.loadtxt(dataname)
plt.figure(figsize=(8, 8))
Umax = np.max(da[:,0])
plt.scatter(da[:,0],da[:,1], s = 20,c = "b")
plt.xlabel(r"$k_x$")
plt.ylabel(r"$k_y$")
plt.title(r"$\mu = $" + format(mu,".2f"))
# plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
#----------------------------------------------------------
def plot_order(mu):
da1 = "fortran-order.dat"
picname = os.path.splitext(da1)[0] + "-mu-" + format(mu,".2f") + ".png"
da1 = np.loadtxt(da1)
plt.figure(figsize=(10, 10))
Umax = np.max(da1[:,0])
plt.scatter(da1[:,0],da1[:,1], s = 20,c = "b",label = "Fortran") # Fortran
plt.xlabel(r"$k_BT$")
plt.ylabel(r"$\Delta_0$")
plt.title(r"$\mu = $" + format(mu,".1f") + r"$\quad U_0 = 1.0$")
plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
plt.legend(loc='best', fontsize = 25, scatterpoints = 1, markerscale = 2) # markerscale 调整点的大小
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
#----------------------------------------------------------
def plot_order_compare(mu):
da1 = "fortran-order.dat"
da2 = "julia-order.dat"
picname = "order-kbt-compare.png"
da1 = np.loadtxt(da1)
da2 = np.loadtxt(da2)
plt.figure(figsize=(10, 10))
Umax = np.max(da1[:,0])
plt.scatter(da1[:,0],da1[:,1], s = 20,c = "b",label = "Fortran") # Fortran
plt.scatter(da2[:,0],da2[:,1], s = 20,c = "r",label = "Julia") # Julia
plt.xlabel(r"$k_BT$")
plt.ylabel(r"$\Delta_0$")
plt.title(r"$\mu = $" + format(mu,".1f") + r"$\quad U_0 = 1.0$")
plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
plt.legend(loc='best', fontsize = 25, scatterpoints = 1, markerscale = 2) # markerscale 调整点的大小
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
#------------------------------------------------------------
if __name__=="__main__":
plot_fs(1.0)
plot_order_compare(1.0)
plot_order(1.0)
解析拟合
超导序参量自洽结果可以通过解析公式拟合,在转变温度$T_c$附近
\[\Delta(T)\approxk\Delta_0\sqrt{\frac{T_c-T}{T}}\] \[\Delta(T)=\Delta_0\tanh(k \sqrt{\frac{T_c-T}{T}})\]这里的$k=1.74$,结果如下图所示
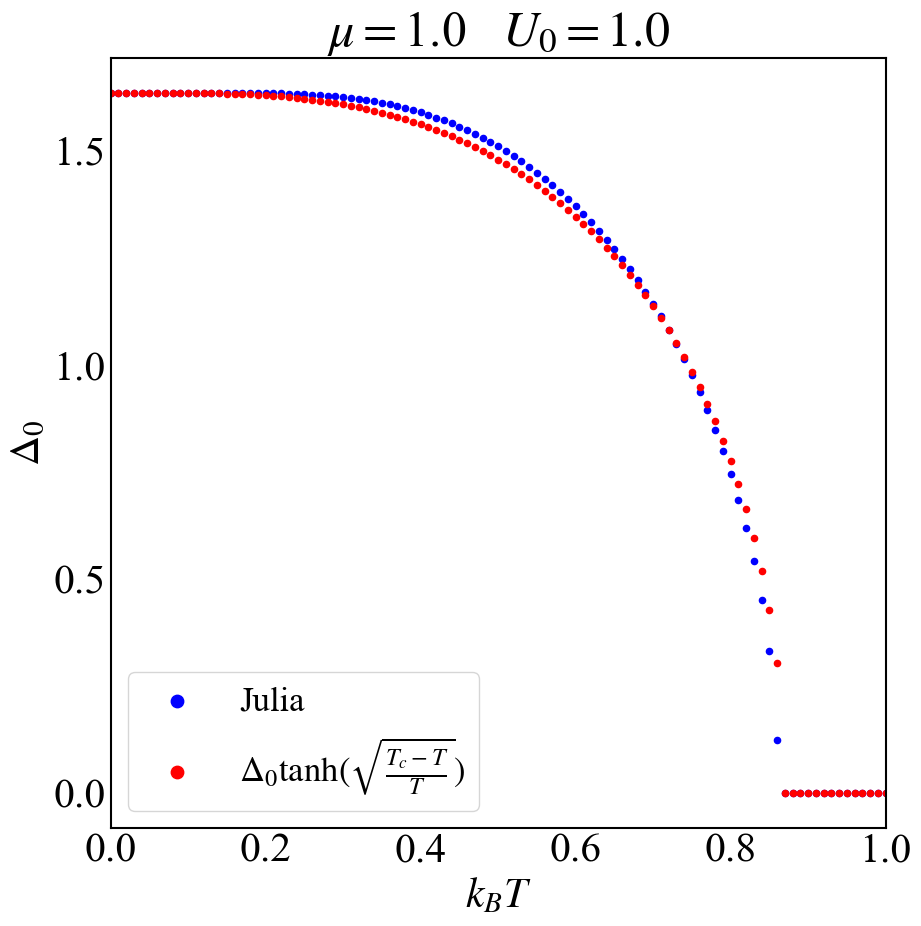
下面是绘图代码
#----------------------------------------------------------
def plot_order_analy(mu):
da1 = "julia-order-kbt.dat"
picname = "order-kbt.png"
da1 = np.loadtxt(da1)
plt.figure(figsize=(10, 10))
Umax = np.max(da1[:,0])
# 解析拟合公式
k0 = 1.74
Tc = 0.87 # 转变温度
da2 = []
for kbt in da1[:,0]:
if kbt < Tc:
da2.append(np.max(da1[:,1]) * np.tanh(k0 * np.sqrt((Tc - kbt)/kbt)))
else:
da2.append(0.0)
plt.scatter(da1[:,0],da1[:,1], s = 20,c = "b",label = "Julia") # Julia
plt.scatter(da1[:,0],da2, s = 20,c = "r",label = r"$\Delta_0\tanh(\sqrt{\frac{T_c-T}{T}})$") # Julia
plt.xlabel(r"$k_BT$")
plt.ylabel(r"$\Delta_0$")
plt.title(r"$\mu = $" + format(mu,".1f") + r"$\quad U_0 = 1.0$")
plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
plt.legend(loc='best', fontsize = 25, scatterpoints = 1, markerscale = 2) # markerscale 调整点的大小
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
若有错误,欢迎指出。感谢李公子以及俊熹的帮助。点击下载文件
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |