整理一下在研究超导序参量的时候,理解傅里叶分析的一些笔记
最近在计算电子配对序参量,其中要分析序参量的配对对称性,这个时候可以采用Fourier变换,分解到不同的$\sin(n\theta)$和$\cos(n\theta)$通道中,通过比较哪个通道的系数最大,就可以确定序参量的位相在动量空间中的依赖关系。不过一般在费米面上绘制出序参量差不多也就可以看出对称性了。
$d_{x^2-y^2}$配对
首先是铜基超导中$d_{x^2-y^2}$电子配对,它的位相在动量空间的变换为
\[\Delta(\theta)=\cos(2\theta)\]考虑将展开
\[\cos(2\theta)=\sum_{\omega_n}C(\omega)e^{i\omega_n\theta}\]因为形式太简单了,所以可以手动进行Fourier展开
\[\cos(2\theta)=e^{i2\theta} + e^{-i2\theta}\]因此可以知道在
\[\omega=2,\qquad \omega=-2\]这两个频率处,Fourier展开系数$C(\omega)$会是最大的。
代码实现
下面就通过代码来演示一下上面的分析


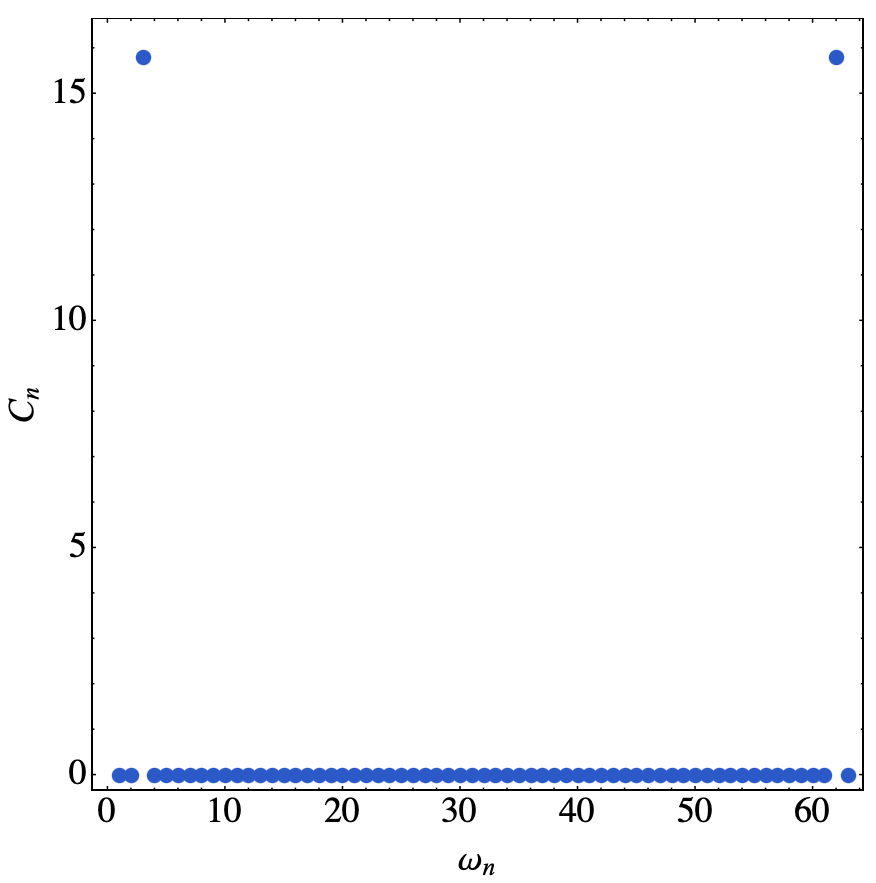
因为这里使用的是Mathematica的离散傅里叶变化,所以这里的$\omega_n$是会依赖于网格间距$dk$的,具体关于离散Fourier变化的算法自己不太懂,但使用这个方法的确是印证了上面的分析。
代码可以点击这里下载
参考文献
- Kohn-Luttinger Mechanism of Superconductivity in Twisted Bilayer WSe$_2$: Gate-Tunable Unconventional Pairing Symmetry
- Quantum Geometric Unconventional Superconductivity
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |