整理一下将库仑势以及屏蔽库仑势通过Fourier变换到实空间时的衰减情况
库伦势
如果电子之间是直接的库伦相互作用,
\[V(\boldsymbol{k})=\frac{1}{|\boldsymbol{k}|}\]该势能随着$\rvert \boldsymbol{k}\rvert $增加而减小,如下图所示
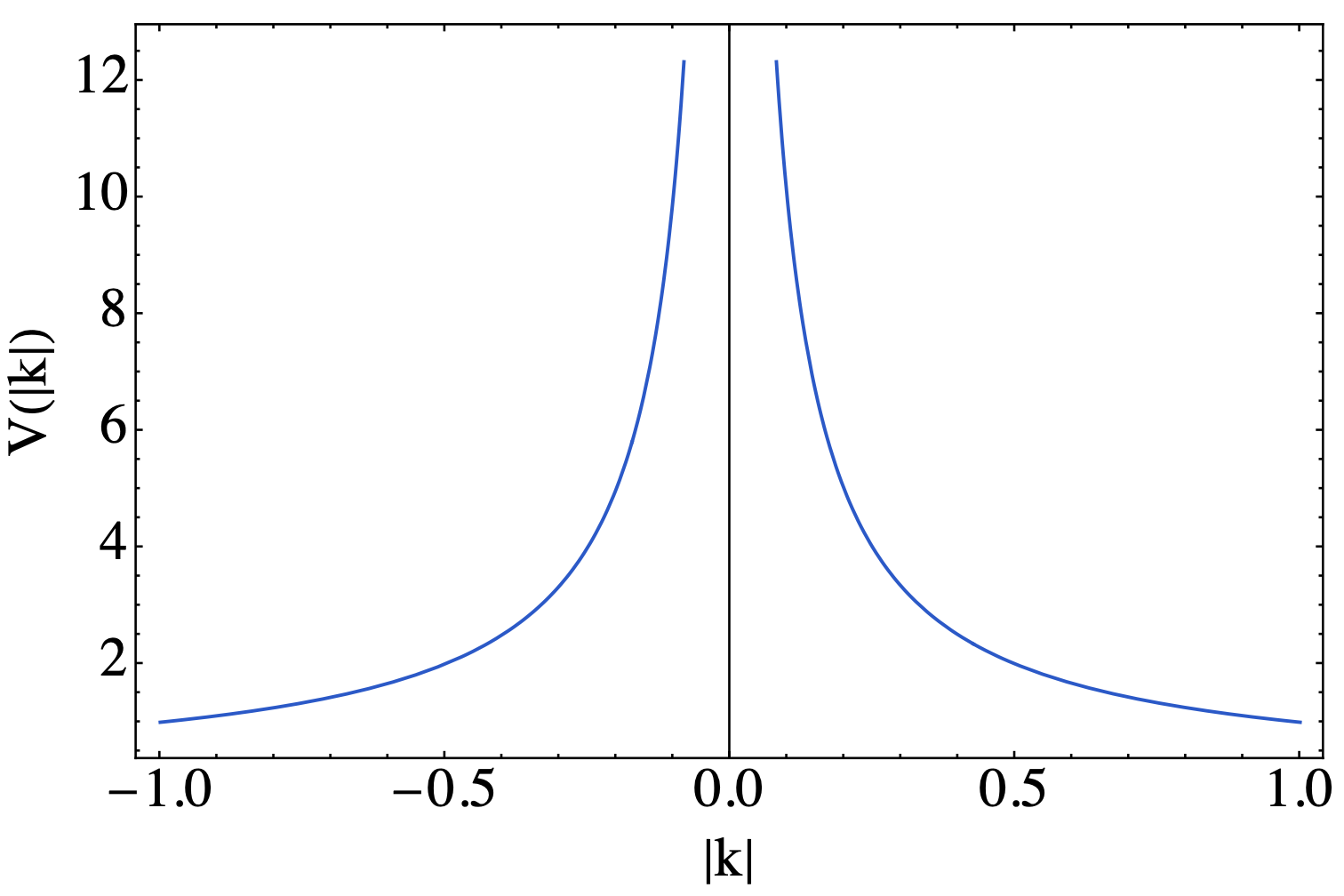
通过Fourier变换到实空间中
\[V(\boldsymbol{r})=\sum_{\boldsymbol{k}}V(\boldsymbol{k})e^{i(\boldsymbol{k}\cdot \boldsymbol{r})}\]这里取$y=0$进行$x$方向进行Fourier变换,得到实空间中库伦势能
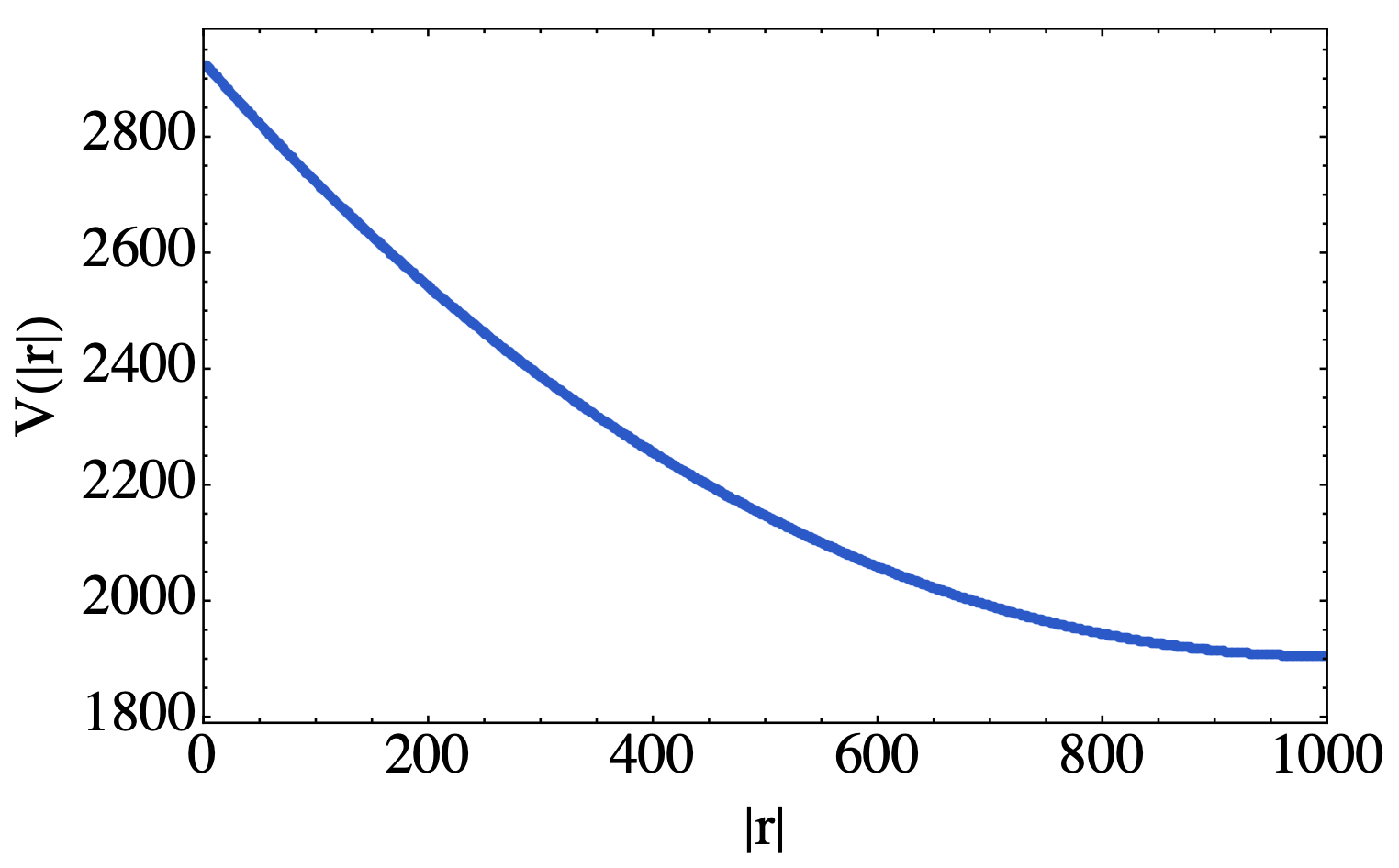
可以看到在$x$比较大的时候,排斥相互作用还是比较强的。
屏蔽库伦势
现在考虑屏蔽库伦势
\[V(\boldsymbol{k})=\frac{1}{\boldsymbol{k}}\tanh(\boldsymbol{k})\]该势能在$\boldsymbol{k}\rightarrow 0$的时候并不是发散的,而是趋近于一个常数,其分布如下图所示

与前面的库伦势相同,对$x$方向做Fourier变换,并取$y=0$,可以得到
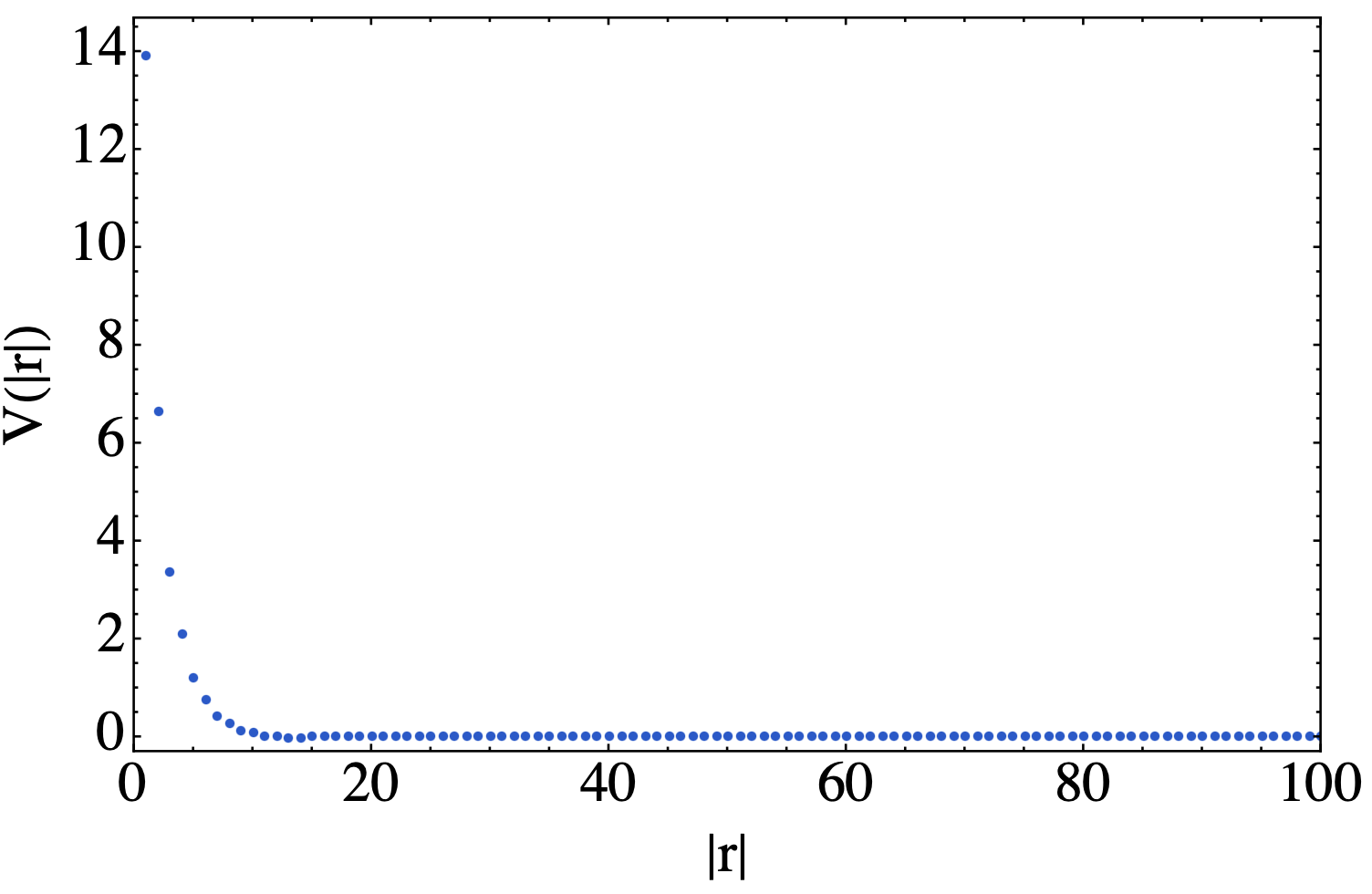
此时可以看到,屏蔽库伦势能在实空间会很快衰减。
代码
这里是用Mathematica做的快速Fourier变换,代码也贴一下

还有比较愚蠢的方式就是自己写程序进行上面的求和过程
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function Set_BZ(kn::Int64)
knn::Int64 = 2 * kn + 1
kmax::Float64 = pi
klist = zeros(Float64,2,knn^2)
ik0 = 0
for ikx in -kn:kn
for iky in -kn:kn
ik0 += 1
klist[1,ik0] = ikx * kmax/kn
klist[2,ik0] = iky * kmax/kn
end
end
return klist
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function Bare_Coulomb_potential(qx::Float64,qy::Float64)
re1::Float64 = 0.0
dd0::Float64 = 40
epsilon::Float64 = 4.0
if (qx == 0 && qy == 0)
# re1 = 2.0 * pi * dd0/epsilon
re1 = 0.0
else
re1 = 2.0 * pi/(epsilon * sqrt(qx^2 + qy^2)) * tanh(dd0 * sqrt(qx^2 + qy^2))
end
return re1
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function Coulomb_Real(ix::Int64,iy::Int64)
kn::Int64 = 1e2
klist = Set_BZ(kn)
re1::ComplexF64 = 0.0
for ik0 in 1:(2 * kn + 1)^2
kx, ky = klist[1,ik0],klist[2,ik0]
re1 += Bare_Coulomb_potential(kx,ky) * exp(im * (kx * ix + ky * iy))
end
return real(re1)/(2 * kn + 1)^2
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function main1()
xn::Int64 = 100
re1 = SharedArray(zeros(Float64, xn, xn))
@sync @distributed for ix in 1:xn
for iy in 1:xn
re1[ix,iy] = Coulomb_Real(ix,iy)
end
end
fx1 = "Real_Coulobm.dat"
f1 = open(fx1,"w")
# x0 = (a->(@sprintf "%15.8f" a)).(re1)
writedlm(f1,re1,"\t")
close(f1)
end
#----------------------------------------------------------------------------------------------------------------------------
@time main1()
实际上用Julia也可以进行快速Fourier变换,这里就还是蠢办法上了。
参考
- 固体理论(李正中) p108
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |