这篇博客整理了几个简单平带模型中量子度规的计算,作为学习笔记整理了一下。
前言
对于一个量子态$\lvert u(\mathbf{k}\rangle$,它的量子几何张量为
\[\begin{equation} \!\!\mathfrak{G}_{ab}\!=\!\langle\partial_{a}u(\mathbf{k})|\partial_{b}u(\mathbf{k})\rangle-\langle\partial_{a}u(\mathbf{k})|u(\mathbf{k})\rangle\langle u(\mathbf{k})|\partial_{b}u(\mathbf{k})\rangle. \end{equation}\]而量子几何张量的实部就是量子度规
\[\begin{equation} \mathcal{G}_{ab}(\mathbf{k})=\mathrm{Re}\left[\langle\partial_{a}u(\mathbf{k})\vert\partial_{b}u(\mathbf{k})\rangle-\langle\partial_{a}u(\mathbf{k})\vert u(\mathbf{k})\rangle\langle u(\mathbf{k})\vert\partial_{b}u(\mathbf{k})\rangle\right], \end{equation}\]度规可调的平带模型
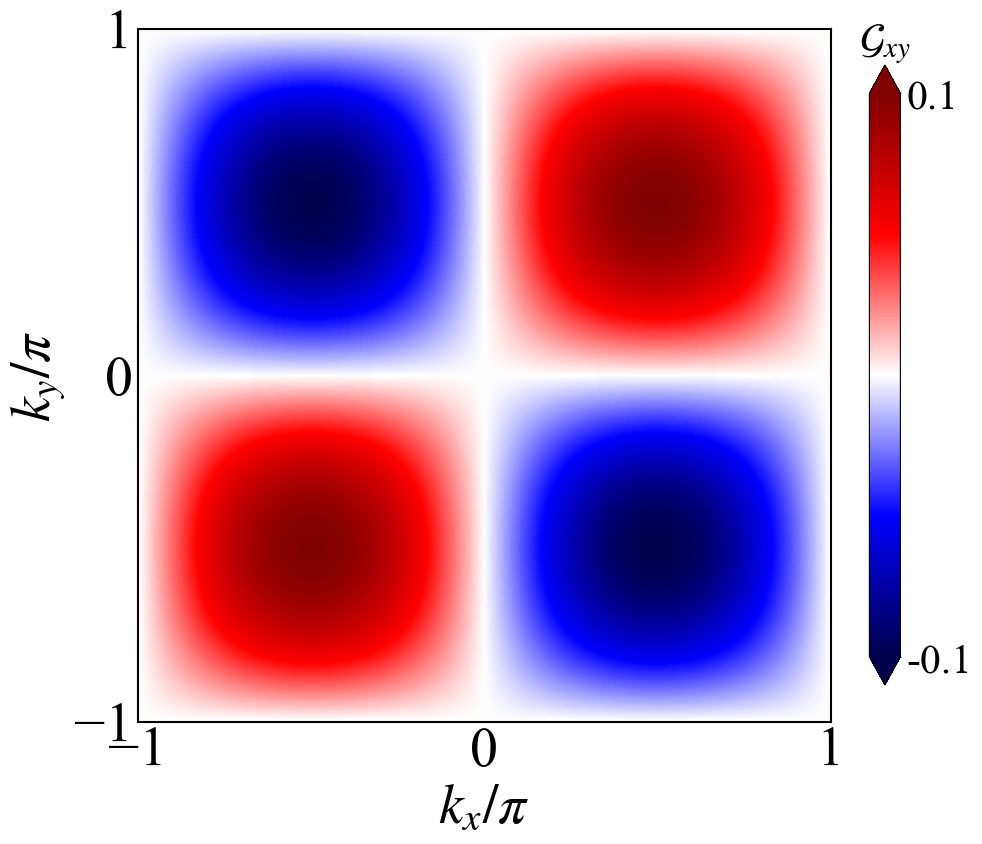
考虑一个拓扑平庸但是度规可调的平带模型
\[\begin{equation} h_s(\mathbf{k})=-t [\sin(\alpha_{\mathbf{k}})\lambda_x+ s_z \cos(\alpha_{\mathbf{k}})\lambda_y]+[-2t_2(\cos k_x+\cos k_y)-\mu]\lambda_0~, \end{equation}\]其中$\alpha(\mathbf{k})=\chi[\cos(k_x a)+\cos(k_y a)]$, $t_2$是最近邻跃迁大小,$\mu$是化学势,$s={ \uparrow,\downarrow }$是自旋指标$s_z=\pm 1$。该哈密顿量具有时间反演对称性$h_{\uparrow}(\mathbf{k})=h^{*}_{\downarrow}(-\mathbf{k})$,其能带色散为
\[\begin{equation} \varepsilon_{\pm}(\mathbf{k})=\pm t+2t_2(\cos k_x+\cos k_y)-\mu \end{equation}\]两个本征波函数为
\[\begin{equation} \vert u_{+}\rangle =\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ i s_ze^{is_z \alpha_{\mathbf{k}}} \end{pmatrix},\\\\\vert u_{-}\rangle =\frac{1}{\sqrt{2}}\begin{pmatrix} -1 \\ i s_ze^{is_z \alpha_{\mathbf{k}}} \end{pmatrix}~. \end{equation}\]结合前面两字几何张量的定义,将本征波函数代入可得
\[\begin{equation} \mathfrak G_{ab}=\frac{1}{4}\partial_a \alpha_{\mathbf{k}}\partial_b \alpha_{\mathbf{k}}. \end{equation}\]从而得到量子度规的解析表达式
\[\begin{equation} \mathcal{G}_{ab}=a^2\chi^2 \sin(k_a)\sin(k_b)/4, \end{equation}\]下面就用代码实现以下
# ========================================================================================================================
# 计算给定模型的量子几何张量
# Ref: Anomalous Coherence Length in Superconductors with Quantum Metric(http://arxiv.org/abs/2308.05686)
# ========================================================================================================================
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function PauliMatrix()
s0 = zeros(ComplexF64,2,2)
sx = zeros(ComplexF64,2,2)
sy = zeros(ComplexF64,2,2)
sz = zeros(ComplexF64,2,2)
s0[1,1] = 1
s0[2,2] = 1
sx[1,2] = 1
sx[2,1] = 1
sy[1,2] = -im
sy[2,1] = im
sz[1,1] = 1
sz[2,2] = -1
return s0,sx,sy,sz
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset(kx::Float64,ky::Float64)::Matrix
t0::Float64 = 1.0
mu::Float64 = 0.0
t2::Float64 = 0.0
chi::Float64 = 0.5
alpha::Float64 = 0.0
hn::Int64 = 2
Ham = zeros(ComplexF64,hn,hn)
alpha = chi * (cos(kx) + cos(ky))
s0,sx,sy,sz = PauliMatrix()
Ham = -t0 * (sin(alpha) * sx + cos(alpha) * sy) + (-2 * t2 * (cos(kx) + cos(ky)) - mu) * s0
return Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset_dkxky(kx::Float64,ky::Float64)
# 计算哈密顿量的导数
hn::Int64 = 2
dk::Float64 = 1E-5
Ham = zeros(ComplexF64,hn,hn)
Hamdk = zeros(ComplexF64,hn,hn)
D_Ham = zeros(ComplexF64,2,hn,hn) # 哈密顿量偏导
# DH_kx
Ham = matset(kx - dk,ky)
Hamdk = matset(kx + dk,ky)
D_Ham[1,:,:] = (Hamdk - Ham)/(2.0 * dk)
# DH_ky
Ham = matset(kx,ky - dk)
Hamdk = matset(kx,ky + dk)
D_Ham[2,:,:] = (Hamdk - Ham)/(2.0 * dk)
return D_Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_cal(kx::Float64,ky::Float64)
# 计算给定能带(bandindex)的量子几何张量(Qxx,Qxy,Qyx,Qyy)
eta::Float64 = 1E-5
ham = matset(kx,ky)
ham_dk = matset_dkxky(kx,ky)
vals,vecs = eigen(ham)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
re1 = zeros(ComplexF64,hn,2,2)
for mu in 1:2,nu in 1:2
for bandindex in 1:hn
for ie in 1:hn
if ie != bandindex
re1[bandindex,mu,nu] += ((vecs[:,bandindex]' * ham_dk[mu,:,:] * vecs[:,ie]) * (vecs[:,ie]' * ham_dk[nu,:,:] * vecs[:,bandindex]))/(vals[bandindex] - vals[ie] + eta)^2
end
end
end
end
return re1
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT(bandindex::Int64)
kn::Int64 = 100
hn::Int64 = 2
klist = range(-pi,pi,length = kn)
kxlist = zeros(Float64,kn^2)
kylist = zeros(Float64,kn^2)
re1 = zeros(ComplexF64,kn^2,hn,2,2)
for ikx in 1:kn,iky in 1:kn
ik0 = Int((ikx - 1) * kn + iky)
kxlist[ik0] = klist[ikx]/pi
kylist[ik0] = klist[iky]/pi
re1[ik0,:,:,:] = QGT_cal(klist[ikx],klist[iky]) # 计算每个动量点上的QGT并存储
end
fx1 ="QGT.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(kxlist)
y0 = (a->(@sprintf "%15.8f" a)).(kylist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex,1,2]))
writedlm(f1,[x0 y0 z0],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_parallel(bandindex::Int64)
kn::Int64 = 100
hn::Int64 = 2
klist = range(-pi,pi,length = kn)
kxlist = SharedArray(zeros(Float64,kn^2))
kylist = SharedArray(zeros(Float64,kn^2))
re1 = SharedArray(zeros(ComplexF64,kn^2,hn,2,2))
@sync @distributed for ikx in 1:kn
for iky in 1:kn
ik0 = Int((ikx - 1) * kn + iky)
kxlist[ik0] = klist[ikx]/pi
kylist[ik0] = klist[iky]/pi
re1[ik0,:,:,:] = QGT_cal(klist[ikx],klist[iky]) # 计算每个动量点上的QGT并存储
end
end
fx1 ="QGT.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(kxlist)
y0 = (a->(@sprintf "%15.8f" a)).(kylist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex,1,2]))
writedlm(f1,[x0 y0 z0],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function main()
return
end
#----------------------------------------------------------------------------------------------------------------------------
@time QGT(2)
绘图
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
import matplotlib.gridspec as gridspec
from matplotlib.path import Path
import matplotlib.colors as mcolors
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#------------------------------------------------------------
def plotQGT():
# dataname = "chi-val-kn-" + str(format(numk,"0>3d")) + ".dat"
dataname = "QGT-lieb.dat"
# dataname = "QGT.dat"
picname = os.path.splitext(dataname)[0] + ".png"
da = np.loadtxt(dataname)
# 使用第一列和第二列分别作为 kx 和 ky
x0 = da[:, 0]
y0 = da[:, 1]
z0 = np.array(da[:, 2])
# 确定坐标范围
xmin, xmax = x0.min(), x0.max()
ymin, ymax = y0.min(), y0.max()
# 假设 kx, ky 网格是方形的,计算网格大小
xn = int(np.sqrt(len(x0)))
# 将 z0 重塑为二维矩阵
z0 = z0.reshape(xn, xn)
plt.figure(figsize=(10, 9))
# 将 extent 参数设置为 (xmin, xmax, ymin, ymax)
sc = plt.imshow(z0, interpolation='bilinear', cmap="Reds", origin='lower', extent=[xmin, xmax, ymin, ymax])
# sc = plt.imshow(z0, interpolation='bilinear', cmap="seismic", origin='lower', extent=[xmin, xmax, ymin, ymax])
# 添加 colorbar
# cb.ax.tick_params(labelsize = 20)
cb = plt.colorbar(sc,fraction = 0.04,ticks = [np.min(z0),np.max(z0)],extend = 'both') # 调整colorbar的大小和图之间的间距
cb.ax.tick_params(size = 1)
cb.ax.set_title(r"Tr[$\mathcal{G}$]",fontsize = 30)
cb.ax.set_yticklabels([format(np.min(z0),".1f"),format(np.max(z0),".1f")])
font2 = {'family': 'Times New Roman', 'weight': 'normal', 'size': 40}
plt.xlabel(r"$k_x/\pi$", font2)
plt.ylabel(r"$k_y/\pi$", font2)
# 隐藏坐标轴刻度值
plt.yticks( fontproperties='Times New Roman', size =40)
plt.xticks( fontproperties='Times New Roman', size = 40)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
# 设置坐标轴的线条宽度
ax = plt.gca()
# 减少 x 和 y 轴上的刻度数量
ax.locator_params(axis='x', nbins = 2) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 2) # y 轴最多显示 3 个刻度
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
# 保存图像
plt.savefig(picname, dpi = 100, bbox_inches='tight')
plt.close()
#------------------------------------------------------------
if __name__=="__main__":
plotQGT()
再给一下Mathematica计算的代码
ClearAll["`*"]
{s0,sx,sy,sz}=PauliMatrix[{0,1,2,3}];
t2=0.0;t=1.0;\[Mu]=0.0;\[Chi]=0.5;
ak=\[Chi](Cos[kx]+Cos[ky]);
H=-t(Sin[ak]sx+Cos[ak]sy)+(-2t2(Cos[kx]+Cos[ky])-\[Mu])s0;
Plot3D[Eigenvalues[H],{kx,-Pi,Pi},{ky,-Pi,Pi},ImageSize->Large,PlotStyle->Directive[Blue,Thickness[0.005]]]
hn=Length[H];(*获取矩阵维度*)
DHkx=D[H,kx];
DHky=D[H,ky];
{vals,vecs}=Eigensystem[H];
QGT[kxx_,kyy_,\[Alpha]_,\[Beta]_]:=Module[{func1,re1},
kx=kxx;ky=kyy;
func1[n_,m_,mat_]:=ConjugateTranspose[{#}&/@vecs[[n]]] . mat . vecs[[m]];
re1=Table[func1[n,m,DHkx] . func1[m,n,DHky]/(vals[[n]]-vals[[m]]+0.0001)^2,{n,1,hn},{m,1,hn}];
re1[[\[Alpha]]][[\[Beta]]]]
QGTRe=Flatten[ParallelTable[{kx,ky,Re[QGT[kx,ky,1,2]]},{kx,-Pi,Pi,0.05},{ky,-Pi,Pi,0.05}],1];
QGTIm=Flatten[ParallelTable[{kx,ky,Im[QGT[kx,ky,1,2]]},{kx,-Pi,Pi,0.05},{ky,-Pi,Pi,0.05}],1];
ListDensityPlot[QGTRe,ColorFunction->"ThermometerColors",PlotLegends->Automatic,FrameStyle->Directive[Black,24,FontFamily->"Times New Roman"],FrameLabel->{Style["\!\(\*SubscriptBox[\(k\), \(x\)]\)",24,
FontFamily->"Times New Roman"],Style["\!\(\*SubscriptBox[\(k\), \(y\)]\)",24,FontFamily->"Times New Roman"]},ClippingStyle->Automatic,ImageSize->Large,FrameTicksStyle->Directive[Black,FontFamily->"Times New Roman",20]]
Lieb模型
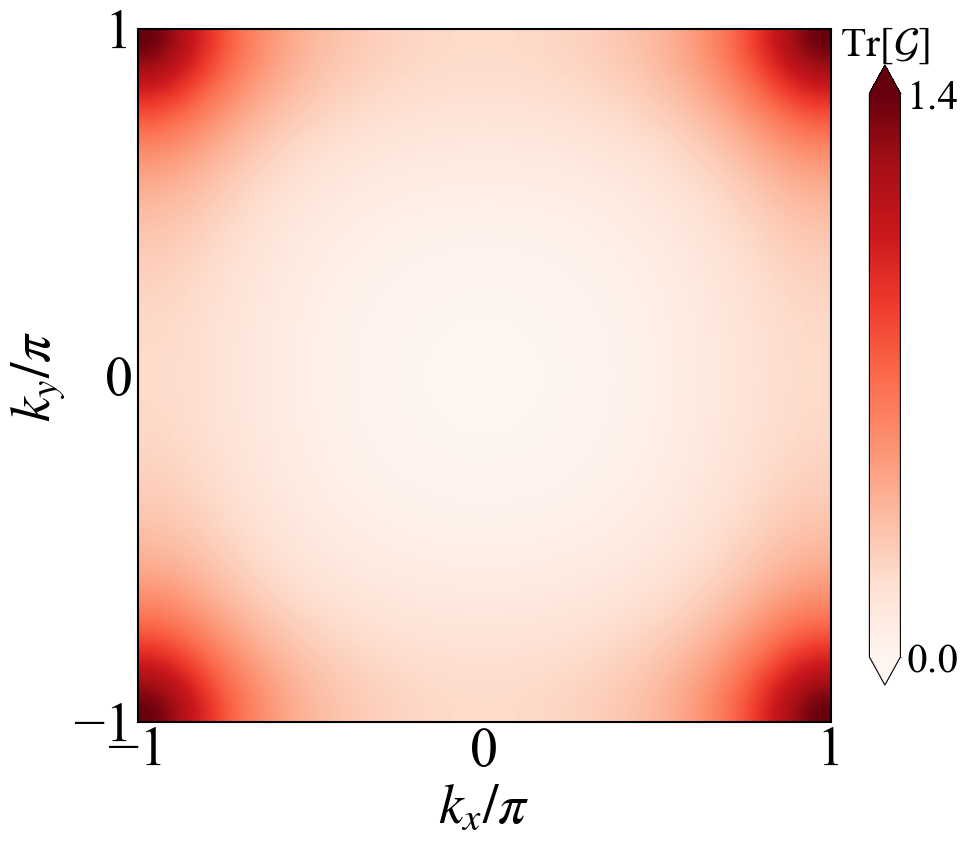
Lieb模型也具有一个平带,但是该模型可以是拓扑非平庸的,这里就只关注其度规部分。哈密顿量为
\[\begin{equation}\left( \begin{array}{cc} 0&f_x&f_2\\ f_x^*&0&f_y\\ f_x^*&f_y^*&0 \end{array}\right) \end{equation}\]其中
\[\begin{equation} \begin{aligned} &f_x=2J(\cos(kx/2) + i\eta\sin(kx/2))\\ & f_y=2J(\cos(ky/2) + i\eta\sin(ky/2))\\ & f_2=2t_2(\cos((k_x+k_y)/2.0) + \cos((k_x-k_y)/2.0)) \end{aligned} \end{equation}\]这里给出Lieb模型量子几何张量实部量子度规的计算
# ========================================================================================================================
# 计算Lieb模型的量子几何张量
# Ref: Anomalous Coherence Length in Superconductors with Quantum Metric(http://arxiv.org/abs/2308.05686)
# ========================================================================================================================
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset(kx::Float64,ky::Float64)::Matrix
J0::Float64 = 1.0
t2::Float64 = 0.0
eta::Float64 = 0.3 * J0
hn::Int64 = 3
Ham = zeros(ComplexF64,hn,hn)
fx = 2 * J0 * (cos(kx/2.0) + im * eta * sin(kx/2.0))
fy = 2 * J0 * (cos(ky/2.0) + im * eta * sin(ky/2.0))
f2 = 2 * t2 * (cos((kx + ky)/2.0) + cos((kx - ky)/2.0))
Ham[1,2] = fx
Ham[1,3] = f2
Ham[2,1] = fx'
Ham[2,3] = fy
Ham[3,1] = f2'
Ham[3,2] = fy'
return Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset_dkxky(hn::Int64,kx::Float64,ky::Float64)
# 计算哈密顿量的导数
dk::Float64 = 1E-5
Ham = zeros(ComplexF64,hn,hn)
Hamdk = zeros(ComplexF64,hn,hn)
D_Ham = zeros(ComplexF64,2,hn,hn) # 哈密顿量偏导
# DH_kx
Ham = matset(kx - dk,ky)
Hamdk = matset(kx + dk,ky)
D_Ham[1,:,:] = (Hamdk - Ham)/(2.0 * dk)
# DH_ky
Ham = matset(kx,ky - dk)
Hamdk = matset(kx,ky + dk)
D_Ham[2,:,:] = (Hamdk - Ham)/(2.0 * dk)
return D_Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_cal(kx::Float64,ky::Float64)
# 计算给定能带(bandindex)的量子几何张量(Qxx,Qxy,Qyx,Qyy)
eta::Float64 = 1E-5
ham = matset(kx,ky)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
ham_dk = matset_dkxky(hn,kx,ky)
vals,vecs = eigen(ham)
re1 = zeros(ComplexF64,hn,2,2)
for mu in 1:2,nu in 1:2
for bandindex in 1:hn
for ie in 1:hn
if ie != bandindex
re1[bandindex,mu,nu] += ((vecs[:,bandindex]' * ham_dk[mu,:,:] * vecs[:,ie]) * (vecs[:,ie]' * ham_dk[nu,:,:] * vecs[:,bandindex]))/(vals[bandindex] - vals[ie] + eta)^2
end
end
end
end
return re1
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT(bandindex::Int64)
kn::Int64 = 100
ham = matset(0.1,0.1)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
klist = range(-pi,pi,length = kn)
kxlist = zeros(Float64,kn^2)
kylist = zeros(Float64,kn^2)
re1 = zeros(ComplexF64,kn^2,hn,2,2)
for ikx in 1:kn,iky in 1:kn
ik0 = Int((ikx - 1) * kn + iky)
kxlist[ik0] = klist[ikx]/pi
kylist[ik0] = klist[iky]/pi
re1[ik0,:,:,:] = QGT_cal(klist[ikx],klist[iky]) # 计算每个动量点上的QGT并存储
end
fx1 ="QGT-lieb.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(kxlist)
y0 = (a->(@sprintf "%15.8f" a)).(kylist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex,1,1] + re1[:,bandindex,2,2]))
writedlm(f1,[x0 y0 z0],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_parallel(bandindex::Int64)
kn::Int64 = 100
hn::Int64 = 2
klist = range(-pi,pi,length = kn)
kxlist = SharedArray(zeros(Float64,kn^2))
kylist = SharedArray(zeros(Float64,kn^2))
re1 = SharedArray(zeros(ComplexF64,kn^2,hn,2,2))
@sync @distributed for ikx in 1:kn
for iky in 1:kn
ik0 = Int((ikx - 1) * kn + iky)
kxlist[ik0] = klist[ikx]/pi
kylist[ik0] = klist[iky]/pi
re1[ik0,:,:,:] = QGT_cal(klist[ikx],klist[iky]) # 计算每个动量点上的QGT并存储
end
end
fx1 ="QGT-lieb.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(kxlist)
y0 = (a->(@sprintf "%15.8f" a)).(kylist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex,1,2]))
writedlm(f1,[x0 y0 z0],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function main()
return
end
#----------------------------------------------------------------------------------------------------------------------------
@time QGT(2) # 第二条能带是平带
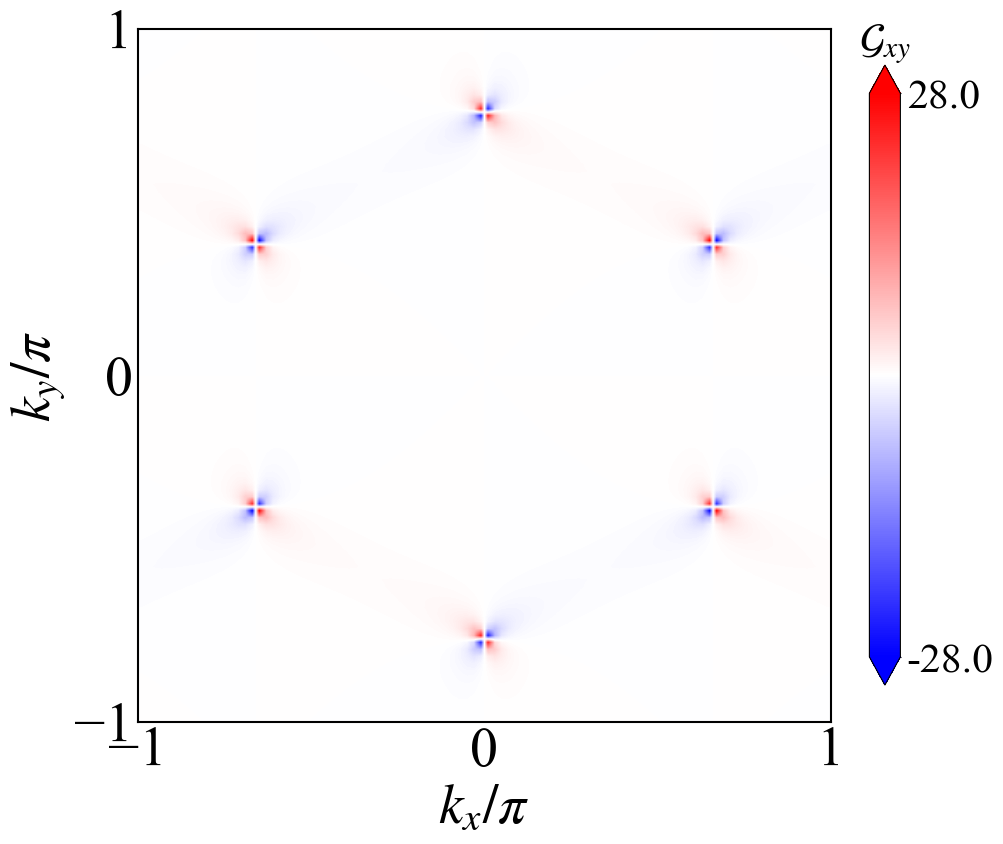
Graphene Quantum Metric
# ========================================================================================================================
# 计算Lieb模型的量子几何张量
# Ref: Anomalous Coherence Length in Superconductors with Quantum Metric(http://arxiv.org/abs/2308.05686)
# ========================================================================================================================
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function PauliMatrix()
s0 = zeros(ComplexF64,2,2)
sx = zeros(ComplexF64,2,2)
sy = zeros(ComplexF64,2,2)
sz = zeros(ComplexF64,2,2)
s0[1,1] = 1
s0[2,2] = 1
sx[1,2] = 1
sx[2,1] = 1
sy[1,2] = -im
sy[2,1] = im
sz[1,1] = 1
sz[2,2] = -1
return s0,sx,sy,sz
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset(kx::Float64,ky::Float64)::Matrix
t1::Float64 = 1.0
delta::Float64 = 0.05
hn::Int64 = 2
Ham = zeros(ComplexF64,hn,hn)
s0,sx,sy,sz = PauliMatrix()
Ham = t1 * (cos(sqrt(3)/2 * kx + 1/2 * ky) + cos(-sqrt(3)/2 * kx + 1/2 * ky) + cos(-ky)) * sx + t1 * (sin(sqrt(3)/2 * kx + 1/2 * ky) + sin(-sqrt(3)/2 * kx + 1/2 * ky) + sin(-ky)) * sy + delta * sz
return Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset_dkxky(hn::Int64,kx::Float64,ky::Float64)
# 计算哈密顿量的导数
dk::Float64 = 1E-5
Ham = zeros(ComplexF64,hn,hn)
Hamdk = zeros(ComplexF64,hn,hn)
D_Ham = zeros(ComplexF64,2,hn,hn) # 哈密顿量偏导
# DH_kx
Ham = matset(kx - dk,ky)
Hamdk = matset(kx + dk,ky)
D_Ham[1,:,:] = (Hamdk - Ham)/(2.0 * dk)
# DH_ky
Ham = matset(kx,ky - dk)
Hamdk = matset(kx,ky + dk)
D_Ham[2,:,:] = (Hamdk - Ham)/(2.0 * dk)
return D_Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_cal(kx::Float64,ky::Float64)
# 计算给定能带(bandindex)的量子几何张量(Qxx,Qxy,Qyx,Qyy)
eta::Float64 = 1E-3
ham = matset(kx,ky)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
ham_dk = matset_dkxky(hn,kx,ky)
vals,vecs = eigen(ham)
re1 = zeros(ComplexF64,hn,2,2)
for mu in 1:2,nu in 1:2
for bandindex in 1:hn
for ie in 1:hn
if ie != bandindex
re1[bandindex,mu,nu] += ((vecs[:,bandindex]' * ham_dk[mu,:,:] * vecs[:,ie]) * (vecs[:,ie]' * ham_dk[nu,:,:] * vecs[:,bandindex]))/(vals[bandindex] - vals[ie] + eta)^2
end
end
end
end
return re1
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT(bandindex::Int64)
kn::Int64 = 100
ham = matset(0.1,0.1)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
klist = range(-pi,pi,length = kn)
kxlist = zeros(Float64,kn^2)
kylist = zeros(Float64,kn^2)
re1 = zeros(ComplexF64,kn^2,hn,2,2)
for ikx in 1:kn,iky in 1:kn
ik0 = Int((ikx - 1) * kn + iky)
kxlist[ik0] = klist[ikx]/pi
kylist[ik0] = klist[iky]/pi
re1[ik0,:,:,:] = QGT_cal(klist[ikx],klist[iky]) # 计算每个动量点上的QGT并存储
end
fx1 ="QGT-graphene.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(kxlist)
y0 = (a->(@sprintf "%15.8f" a)).(kylist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex,1,2]))
z1 = (a->(@sprintf "%15.8f" a)).(imag(re1[:,bandindex,1,2]))
writedlm(f1,[x0 y0 z0 z1],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_parallel(bandindex::Int64)
kn::Int64 = 100
hn::Int64 = 2
klist = range(-pi,pi,length = kn)
kxlist = SharedArray(zeros(Float64,kn^2))
kylist = SharedArray(zeros(Float64,kn^2))
re1 = SharedArray(zeros(ComplexF64,kn^2,hn,2,2))
@sync @distributed for ikx in 1:kn
for iky in 1:kn
ik0 = Int((ikx - 1) * kn + iky)
kxlist[ik0] = klist[ikx]/pi
kylist[ik0] = klist[iky]/pi
re1[ik0,:,:,:] = QGT_cal(klist[ikx],klist[iky]) # 计算每个动量点上的QGT并存储
end
end
fx1 ="QGT-lieb.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(kxlist)
y0 = (a->(@sprintf "%15.8f" a)).(kylist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex,1,2]))
z1 = (a->(@sprintf "%15.8f" a)).(imag(re1[:,bandindex,1,2]))
writedlm(f1,[x0 y0 z0 z1],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function main()
return
end
#----------------------------------------------------------------------------------------------------------------------------
@time QGT(2)
Sawtooth模型
Sawtooth模型的晶格结构如下图所示
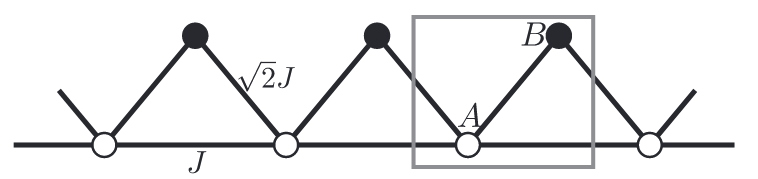
每个原胞内有两个轨道$(A,B)$,其哈密顿量为
\[\begin{equation} \left[ \begin{array}{cc} 2J_0 \cos(k)-\mu & 2\sqrt{2}J_0\cos(k/2)\\ 2\sqrt{2}J_0\cos(k/2)& -\mu \end{array} \right] \end{equation}\]该模型两个能带的度规是相同的
\[\begin{equation} g=\frac{1-\cos(k)}{2(2+\cos(k))^2} \end{equation}\]下面直接上数值计算的代码了
# ========================================================================================================================
# 计算Sawthhod 模型的量子度规
# Ref: Wave-packet dynamics of Bogoliubov quasiparticles: Quantum metric effects(https://link.aps.org/doi/10.1103/PhysRevB.96.064511)
# ========================================================================================================================
@everywhere using SharedArrays,LinearAlgebra,Distributed,DelimitedFiles,Printf,BenchmarkTools,Arpack,Dates
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset(kx::Float64,)::Matrix
J0::Float64 = 1.0
mu::Float64 = -2
hn::Int64 = 2
Ham = zeros(ComplexF64,hn,hn)
Ham[1,1] = 2 * J0 * cos(kx) - mu
Ham[1,2] = 2 * J0 * cos(kx/2.0)
Ham[2,1] = 2 * J0 * cos(kx/2.0)
Ham[2,2] = -mu
return Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function matset_dkxky(hn::Int64,kx::Float64)
# 计算哈密顿量的导数
dk::Float64 = 1E-5
Ham = zeros(ComplexF64,hn,hn)
Hamdk = zeros(ComplexF64,hn,hn)
D_Ham = zeros(ComplexF64,hn,hn) # 哈密顿量偏导
# DH_kx
Ham = matset(kx - dk)
Hamdk = matset(kx + dk)
D_Ham = (Hamdk - Ham)/(2.0 * dk)
return D_Ham
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT_cal(kx::Float64,)
# 计算给定能带(bandindex)的量子几何张量(Qxx)
eta::Float64 = 1E-3
ham = matset(kx)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
ham_dk = matset_dkxky(hn,kx)
vals,vecs = eigen(ham)
re1 = zeros(ComplexF64,hn)
for bandindex in 1:hn
for ie in 1:hn
if ie != bandindex
re1[bandindex] += ((vecs[:,bandindex]' * ham_dk * vecs[:,ie]) * (vecs[:,ie]' * ham_dk * vecs[:,bandindex]))/(vals[bandindex] - vals[ie] + eta)^2
end
end
end
return re1
end
#----------------------------------------------------------------------------------------------------------------------------
@everywhere function QGT(bandindex::Int64)
kn::Int64 = 2E2
ham = matset(0.1)
hn = size(ham)[1] # 根据哈密顿量来确定矩阵维度
klist = range(-pi,pi,length = kn)
re1 = SharedArray(zeros(ComplexF64,kn,hn))
re2 = SharedArray(zeros(Float64,kn))
@sync @distributed for ikx in 1:kn
kx = klist[ikx]/pi
re1[ikx,:] = QGT_cal(kx) # 计算每个动量点上的QGT并存储
re2[ikx] = (1 - cos(kx))/(2(2 + cos(kx))^2) # 解析结果
end
fx1 ="QGT-Sawthhod.dat"
f1 = open(fx1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(klist)
z0 = (a->(@sprintf "%15.8f" a)).(real(re1[:,bandindex]))
z1 = (a->(@sprintf "%15.8f" a)).(imag(re1[:,bandindex]))
z2 = (a->(@sprintf "%15.8f" a)).(real(re2))
writedlm(f1,[x0 z0 z1 z2],"\t")
close(f1)
return
end
#----------------------------------------------------------------------------------------------------------------------------
@time QGT(1)
绘图代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
import matplotlib.gridspec as gridspec
from matplotlib.path import Path
import matplotlib.colors as mcolors
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#---------------------------------------------------------------------------------------------------------------------------------------------------------
def plot_QGT_Sawthhod():
dataname = "QGT-Sawthhod.dat"
picname = os.path.splitext(dataname)[0] + ".png"
da = np.loadtxt(dataname)
# 使用第一列和第二列分别作为 kx 和 ky
x0 = da[:, 0]
y0 = da[:, 1] # Quantum Metric numerical
y1 = da[:, 3] # Quantum Metric analy
plt.figure(figsize=(10, 9))
num_ticks = 3
Umax = np.max(da[:,0])
Umin = np.min(da[:,0])
plt.scatter(x0,y0,c = "b", marker = "*", label = r"Numerical")
plt.scatter(x0,y1,c = "r", marker = "h", label = r"Analcial")
plt.xlabel(r"$k$")
plt.ylabel(r"$\mathcal{G}_{xx}$")
plt.xlim(Umin,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
plt.legend(loc='best', fontsize = 30, markerscale = 2)
# plt.axis('scaled')
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
ax.locator_params(axis='x', nbins = num_ticks) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = num_ticks) # y 轴最多显示 3 个刻度
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
数值结果与解析结果对比
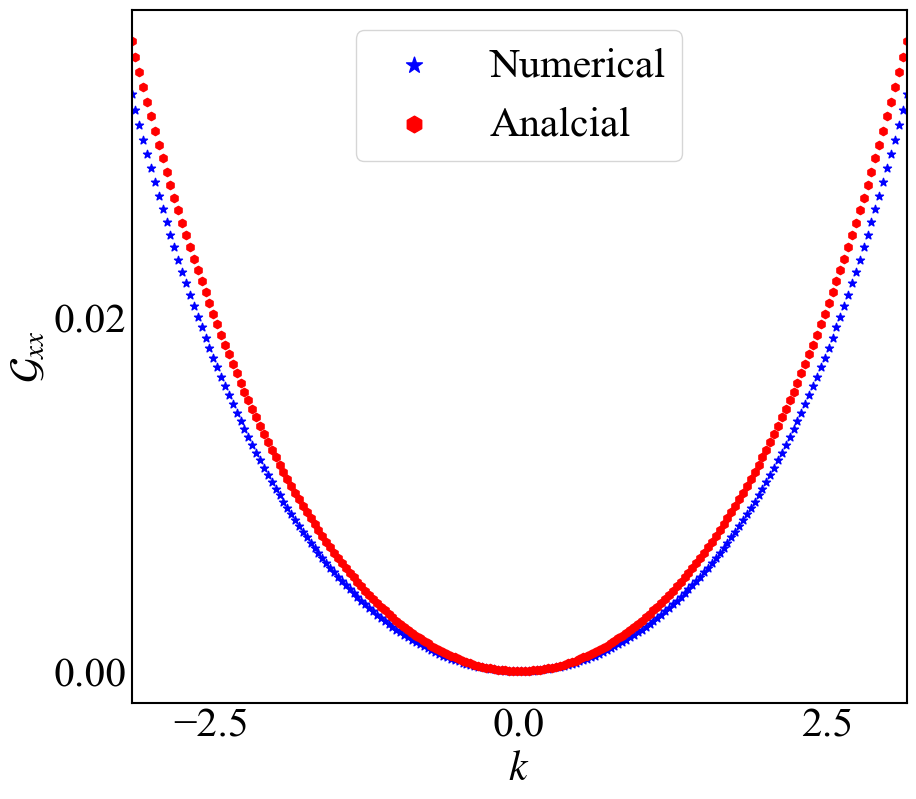
参考文献
- Anomalous Coherence Length in Superconductors with Quantum Metric
- Wave-packet dynamics of Bogoliubov quasiparticles: Quantum metric effects
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |