整理用Fortran计算某一条能带的Hall电导,这里使用的QWZ模型。
前言
这里使用的是最简单的QWZ模型,其哈密顿量为
\[H = (m_0 - t_x \cos(k_x) - t_y \cos(k_y))\sigma_z + a_x \sin(k_x) \sigma_x + a_y * \sin(k_y) * sigma_y\]程序实现上目前是分别计算每一条能带的Hall电导,而不是计算费米面以下电子贡献的电导。当化学势落在能隙中的时候,这里计算的Hall电导就是单独一条能带贡献,如果化学势与能带有交点,那么Hall电导的计算应该是考虑所有费米面以下的贡献,这里先不考虑这件事情。
代码
串行版
module code_param
implicit none
integer, parameter :: dp = kind(1.0d0) ! 双精度
real(dp),parameter::pi = acos(-1.0_dp)
complex(dp),parameter::im = (0.,1.) ! Imagine unit
integer Nk,numk_bz
real(dp),allocatable::BZklist(:,:)
real(dp) m0,t1,ax,ay,mu
real(dp) omega
parameter(m0 = 1.0,t1 = 1.0,ax = 1.0,ay = 1.0,Nk = 1e2, mu = 0.0, omega = 1e-8)
end module code_param
!==============================================================================================================================================================
program chern_insulator_hall_conductance
use code_param
implicit none
integer :: ik0
real(dp) :: kx, ky, hall_conductance
real(dp),external :: calculate_berry_curvature
call squareBZ() ! 构建布里渊区
hall_conductance = 0.0
! 遍历 k 空间,计算 Berry 曲率并积分
do ik0 = 1,size(BZklist,2)
kx = BZklist(1,ik0)
ky = BZklist(2,ik0)
hall_conductance = hall_conductance + calculate_berry_curvature(kx,ky,1) * (pi/Nk)**2
end do
! 输出结果
write(*,"(A50,F15.6)")"Hall Conductance (in units of e^2/h): ", hall_conductance / (2.0 * pi)
end program chern_insulator_hall_conductance
!==============================================================================================================================================================
function calculate_berry_curvature(kx,ky,ind_band)
! 计算某一条能带的 Berry 曲率的子程序
use code_param
implicit none
integer,parameter::hn = 2 ! 哈密顿量维度
integer ie1,ie2
real(dp), intent(in) :: kx, ky
integer, intent(in) :: ind_band
real(dp) :: eigvals(hn),calculate_berry_curvature
complex(dp) :: re1(hn), dHdkx(hn,hn), dHdky(hn,hn), Ham(hn,hn), eigvecs(hn,hn)
complex(dp),external::Ave_Ham
! H = (m0 - tx cos(kx) - ty cos(ky))\sigma_z + ax sin(kx) \sigma_x + ay * sin(ky) * sigma_y
Ham = 0.0
Ham(1,1) = m0 - t1 * (cos(kx) + cos(ky)) - mu
Ham(2,2) = -(m0 - t1 * (cos(kx) + cos(ky))) - mu
Ham(1,2) = ax * sin(kx) - im * ay * sin(ky)
Ham(2,1) = ax * sin(kx) + im * ay * sin(ky)
! 计算哈密顿量的特征值和特征向量
eigvecs = 0.0
eigvals = 0.0
call diagonalize_hermitian_matrix(hn, Ham, eigvecs, eigvals)
! 构建哈密顿量对 kx 和 ky 的导数矩阵
dHdkx = 0.0
dHdky = 0.0
! DH_x
dHdkx(1,1) = t1 * sin(kx)
dHdkx(2,2) = -t1 * sin(kx)
dHdkx(1,2) = ax * cos(kx)
dHdkx(2,1) = ax * cos(kx)
! DH_y
dHdky(1,1) = t1 * sin(ky)
dHdky(2,2) = -t1 * sin(ky)
dHdky(1,2) = -im * ay * cos(ky)
dHdky(2,1) = im * ay * cos(ky)
! 计算 Berry 曲率
re1 = 0.0
do ie1 = 1, hn ! 索引能带
do ie2 = 1, hn
if (ie2 /= ie1) then
re1(ie1) = re1(ie1) + (Ave_Ham(hn, eigvecs(:, ie1), dHdkx, eigvecs(:, ie2)) * &
Ave_Ham(hn, eigvecs(:, ie2), dHdky, eigvecs(:, ie1))) / &
((eigvals(ie1) - eigvals(ie2))**2 + omega) ! 添加正则项防止除零
endif
end do
end do
calculate_berry_curvature = 2 * aimag(re1(ind_band))
end function calculate_berry_curvature
!==============================================================================================================================================================
function Ave_Ham(matdim,psi1,Ham,psi2)
! 计算 <psi_1|Ham|psi_2>
use code_param
implicit none
integer i0,j0,matdim
complex(dp) Ave_Ham,expectation,Ham(matdim,matdim),temp(matdim),psi1(matdim),psi2(matdim)
expectation = 0.0
do i0 = 1,matdim
temp(i0) = 0.0
do j0 = 1,matdim
temp(i0) = temp(i0) + Ham(i0, j0) * psi2(j0)
end do
end do
do i0 = 1,matdim
expectation = expectation + conjg(psi1(i0)) * temp(i0)
end do
Ave_Ham = expectation
return
end function
!============================================================================================================================
subroutine squareBZ()
! 构建四方BZ
use code_param
integer ikx,iky,i0
! 对于四方点阵,BZ的点数可以直接确定
numk_bz = (2 * Nk)**2
allocate(BZklist(2,numk_bz))
i0 = 0
open(30,file = "BZ.dat")
do ikx = -Nk,Nk - 1
do iky = -Nk,Nk - 1
i0 = i0 + 1
BZklist(1,i0) = pi * ikx/(1.0 * Nk)
BZklist(2,i0) = pi * iky/(1.0 * Nk)
write(30,"(4F15.8)")BZklist(1,i0),BZklist(2,i0)
end do
end do
close(30)
return
end subroutine
!==============================================================================================================================================================
subroutine diagonalize_Hermitian_matrix(matdim, matin, matout, mateigval)
! 厄米矩阵对角化
! matin 输入矩阵, matout 本征矢量, mateigval 本征值
implicit none
integer, parameter :: dp = kind(1.0d0) ! 双精度
integer, intent(in) :: matdim
integer :: lda0, lwmax0, lwork, lrwork, liwork, info
complex(dp), intent(in) :: matin(matdim, matdim)
complex(dp), intent(out) :: matout(matdim, matdim)
real(dp), intent(out) :: mateigval(matdim)
complex(dp), allocatable :: work(:)
real(dp), allocatable :: rwork(:)
integer, allocatable :: iwork(:)
!-----------------
lda0 = matdim
lwmax0 = 2 * matdim + matdim**2
allocate(work(lwmax0))
allocate(rwork(1 + 5 * matdim + 2 * matdim**2))
allocate(iwork(3 + 5 * matdim))
matout = matin
lwork = -1
liwork = -1
lrwork = -1
! 初次调用 zheevd 获取最佳工作空间大小
call zheevd('V', 'U', matdim, matout, lda0, mateigval, work, lwork, rwork, lrwork, iwork, liwork, info)
! 根据第一次调用的返回值重新调整工作空间大小
lwork = min(2 * matdim + matdim**2, int(work(1)))
lrwork = min(1 + 5 * matdim + 2 * matdim**2, int(rwork(1)))
liwork = min(3 + 5 * matdim, iwork(1))
! 重新分配工作空间
deallocate(work)
allocate(work(lwork))
deallocate(rwork)
allocate(rwork(lrwork))
deallocate(iwork)
allocate(iwork(liwork))
! 第二次调用 zheevd 计算本征值和本征矢量
call zheevd('V', 'U', matdim, matout, lda0, mateigval, work, lwork, rwork, lrwork, iwork, liwork, info)
! 错误处理
if (info > 0) then
open(11, file = "mes.dat", status = "unknown")
write(11, *) 'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine diagonalize_Hermitian_matrix
并行版
module code_param
implicit none
integer, parameter :: dp = kind(1.0d0) ! 双精度
real(dp),parameter::pi = acos(-1.0_dp)
complex(dp),parameter::im = (0.,1.) ! Imagine unit
real(dp), parameter :: e0 = 1.602176634e-19_dp ! 电子电荷 (C)
real(dp), parameter :: hbar = 1.0545718e-34_dp ! 约化普朗克常数 (J·s)
integer Nk,numk_bz,num_mu
real(dp),allocatable::BZklist(:,:)
real(dp) m0,t1,ax,ay,mu,mu_Max
real(dp) omega,delta_k
parameter(t1 = 1.0,ax = 1.0,mu = 0.0,ay = 1.0,Nk = 1e3, omega = 1e-8, delta_k = 1e-5,num_mu = 100,mu_max = 3)
end module code_param
!==============================================================================================================================================================
program main
use code_param
use mpi
implicit none
integer numcore,indcore,ierr,nki,nkf ! Parameter for MPI
integer i0
real(dp) temp,hall_conductance
real(dp),external::calculate_Hall_conductance
real(dp) da_mpi(num_mu),da_list(num_mu),hall_mpi(num_mu),hall_list(num_mu)
!####################################### 并行计算设置 #######################################
call MPI_INIT(ierr) ! 初始化进程
call MPI_COMM_RANK(MPI_COMM_WORLD, indcore, ierr) ! 得到本进程在通信空间中的rank值,即在组中的逻辑编号(该indcore为0到numcore-1间的整数,相当于进程的ID。)
call MPI_COMM_SIZE(MPI_COMM_WORLD, numcore, ierr) !获得进程数量,用numcoer保存
! 并行循环分拆
nki = floor(indcore * (1.0 * num_mu)/numcore) + 1
nkf = floor((indcore + 1) * (1.0 * num_mu)/numcore)
!####################################### 并行计算设置 #######################################
call squareBZ() ! 构建布里渊区
do i0 = nki,nkf
m0 = 2.0 * mu_max/num_mu * i0 - mu_max
da_mpi(i0) = m0
hall_mpi(i0) = calculate_Hall_conductance()
end do
call MPI_Barrier(MPI_COMM_WORLD,ierr) ! 等所有核心都计算完成
call MPI_Reduce(da_mpi, da_list, num_mu, MPI_DOUBLE_PRECISION, MPI_SUM, 0, MPI_COMM_WORLD,ierr)
call MPI_Reduce(hall_mpi, hall_list, num_mu, MPI_DOUBLE_PRECISION, MPI_SUM, 0, MPI_COMM_WORLD,ierr)
if(indcore.eq.0)then
! 数据读写
open(30,file = "Hall-mu.dat")
do i0 = 1,num_mu
write(30,"(9F20.10)")da_list(i0),hall_list(i0)
enddo
close(30)
endif
call MPI_Finalize(ierr)
! hall_conductance = calculate_Hall_conductance()
! 输出结果
! write(*,"(A50,F15.6)")"Hall Conductance (in units of e^2/h): ", hall_conductance
end program main
!==============================================================================================================================================================
function calculate_Hall_conductance()
use code_param
implicit none
integer :: ik0
real(dp) :: kx, ky, re1, re2, calculate_Hall_conductance
real(dp),external :: calculate_berry_curvature_v1
real(dp),external :: calculate_berry_curvature_v2
re1 = 0.0
re2 = 0.0
! 遍历 k 空间,计算 Berry 曲率并积分
do ik0 = 1,size(BZklist,2)
kx = BZklist(1,ik0)
ky = BZklist(2,ik0)
! re2 = re2 + calculate_berry_curvature_v1(kx,ky,1) * (pi/Nk)**2 ! 我这里的步长上是 pi/Nk
re1 = re1 + calculate_berry_curvature_v2(kx,ky,1) * (pi/Nk)**2 ! 我这里的步长上是 pi/Nk
end do
calculate_Hall_conductance = re1/(2.0 * pi)
! 输出结果
! write(*,"(A50,F15.6)")"Hall Conductance (in units of e^2/h): ", re1/(2 * pi)
end function calculate_Hall_conductance
!==============================================================================================================================================================
function calculate_berry_curvature_v1(kx,ky,ind_band)
! 计算某一条能带的 Berry 曲率的子程序
! 解析给出哈密顿量偏导
use code_param
implicit none
integer,parameter::hn = 2 ! 哈密顿量维度
integer ie1,ie2
real(dp), intent(in) :: kx, ky
integer, intent(in) :: ind_band
real(dp) :: eigvals(hn),calculate_berry_curvature_v1
complex(dp) :: re1(hn), dHdkx(hn,hn), dHdky(hn,hn), Ham(hn,hn), eigvecs(hn,hn)
complex(dp),external::Ave_Ham
! H = (m0 - tx cos(kx) - ty cos(ky))\sigma_z + ax sin(kx) \sigma_x + ay * sin(ky) * sigma_y
Ham = 0.0
Ham(1,1) = m0 - t1 * (cos(kx) + cos(ky)) - mu
Ham(2,2) = -(m0 - t1 * (cos(kx) + cos(ky))) - mu
Ham(1,2) = ax * sin(kx) - im * ay * sin(ky)
Ham(2,1) = ax * sin(kx) + im * ay * sin(ky)
! 计算哈密顿量的特征值和特征向量
eigvecs = 0.0
eigvals = 0.0
call diagonalize_hermitian_matrix(hn, Ham, eigvecs, eigvals)
! 构建哈密顿量对 kx 和 ky 的导数矩阵
dHdkx = 0.0
dHdky = 0.0
! DH_x
dHdkx(1,1) = t1 * sin(kx)
dHdkx(2,2) = -t1 * sin(kx)
dHdkx(1,2) = ax * cos(kx)
dHdkx(2,1) = ax * cos(kx)
! DH_y
dHdky(1,1) = t1 * sin(ky)
dHdky(2,2) = -t1 * sin(ky)
dHdky(1,2) = -im * ay * cos(ky)
dHdky(2,1) = im * ay * cos(ky)
! 计算 Berry 曲率
re1 = 0.0
do ie1 = 1, hn ! 索引能带
do ie2 = 1, hn
if (ie2 /= ie1) then
re1(ie1) = re1(ie1) + (Ave_Ham(hn, eigvecs(:, ie1), dHdkx, eigvecs(:, ie2)) * &
Ave_Ham(hn, eigvecs(:, ie2), dHdky, eigvecs(:, ie1))) / &
((eigvals(ie1) - eigvals(ie2))**2 + omega) ! 添加正则项防止除零
endif
end do
end do
calculate_berry_curvature_v1 = 2 * aimag(re1(ind_band))
end function calculate_berry_curvature_v1
!==============================================================================================================================================================
function calculate_berry_curvature_v2(kx,ky,ind_band)
! 计算某一条能带的 Berry 曲率的子程序
! 数值差分计算哈密顿量偏导
use code_param
implicit none
integer,parameter::hn = 2 ! 哈密顿量维度
integer ie1,ie2
real(dp), intent(in) :: kx, ky
integer, intent(in) :: ind_band
real(dp) :: eigvals(hn),calculate_berry_curvature_v2
complex(dp) :: re1(hn), dHdkx(hn,hn), dHdky(hn,hn), Ham(hn,hn), eigvecs(hn,hn)
complex(dp),external::Ave_Ham
call matset(kx,ky,Ham)
call DH_kxky(kx,ky,dHdkx,dHdky)
! 计算哈密顿量的特征值和特征向量
eigvecs = 0.0
eigvals = 0.0
call diagonalize_hermitian_matrix(hn, Ham, eigvecs, eigvals)
! 计算 Berry 曲率
re1 = 0.0
do ie1 = 1, hn ! 索引能带
do ie2 = 1, hn
if (ie2 /= ie1) then
re1(ie1) = re1(ie1) + (Ave_Ham(hn, eigvecs(:, ie1), dHdkx, eigvecs(:, ie2)) * &
Ave_Ham(hn, eigvecs(:, ie2), dHdky, eigvecs(:, ie1))) / &
((eigvals(ie1) - eigvals(ie2))**2 + omega) ! 添加正则项防止除零
endif
end do
end do
calculate_berry_curvature_v2 = 2 * aimag(re1(ind_band))
end function calculate_berry_curvature_v2
!==============================================================================================================================================================
subroutine matset(kx,ky,Ham)
use code_param
implicit none
integer,parameter::hn = 2 ! 哈密顿量维度
real(dp) kx,ky
complex(dp) :: Ham(hn,hn)
! H = (m0 - tx cos(kx) - ty cos(ky))\sigma_z + ax sin(kx) \sigma_x + ay * sin(ky) * sigma_y
Ham = 0.0
Ham(1,1) = m0 - t1 * (cos(kx) + cos(ky)) - mu
Ham(2,2) = -(m0 - t1 * (cos(kx) + cos(ky))) - mu
Ham(1,2) = ax * sin(kx) - im * ay * sin(ky)
Ham(2,1) = ax * sin(kx) + im * ay * sin(ky)
return
end subroutine
!==============================================================================================================================================================
subroutine DH_kxky(kx,ky,Ham_dkx,Ham_dky)
use code_param
implicit none
integer,parameter::hn = 2 ! 哈密顿量维度
real(dp) kx,ky
complex(dp) :: Ham_pk(hn,hn),Ham_mk(hn,hn),Ham_dkx(hn,hn),Ham_dky(hn,hn)
call matset(kx + delta_k,ky,Ham_pk)
call matset(kx - delta_k,ky,Ham_mk)
Ham_dkx = (Ham_pk - Ham_mk)/(2.0 * delta_k)
call matset(kx,ky + delta_k,Ham_pk)
call matset(kx,ky - delta_k,Ham_mk)
Ham_dky = (Ham_pk - Ham_mk)/(2.0 * delta_k)
return
end subroutine
!==============================================================================================================================================================
function Ave_Ham(matdim,psi1,Ham,psi2)
! 计算 <psi_1|Ham|psi_2>
use code_param
implicit none
integer i0,j0,matdim
complex(dp) Ave_Ham,expectation,Ham(matdim,matdim),temp(matdim),psi1(matdim),psi2(matdim)
expectation = 0.0
do i0 = 1,matdim
temp(i0) = 0.0
do j0 = 1,matdim
temp(i0) = temp(i0) + Ham(i0, j0) * psi2(j0)
end do
end do
do i0 = 1,matdim
expectation = expectation + conjg(psi1(i0)) * temp(i0)
end do
Ave_Ham = expectation
return
end function
!============================================================================================================================
subroutine squareBZ()
! 构建四方BZ
use code_param
integer ikx,iky,i0
! 对于四方点阵,BZ的点数可以直接确定
numk_bz = (2 * Nk)**2
allocate(BZklist(2,numk_bz))
i0 = 0
open(30,file = "BZ.dat")
do ikx = -Nk,Nk - 1
do iky = -Nk,Nk - 1
i0 = i0 + 1
BZklist(1,i0) = pi * ikx/(1.0 * Nk)
BZklist(2,i0) = pi * iky/(1.0 * Nk)
write(30,"(4F15.8)")BZklist(1,i0),BZklist(2,i0)
end do
end do
close(30)
return
end subroutine
!==============================================================================================================================================================
subroutine diagonalize_Hermitian_matrix(matdim, matin, matout, mateigval)
! 厄米矩阵对角化
! matin 输入矩阵, matout 本征矢量, mateigval 本征值
implicit none
integer, parameter :: dp = kind(1.0d0) ! 双精度
integer, intent(in) :: matdim
integer :: lda0, lwmax0, lwork, lrwork, liwork, info
complex(dp), intent(in) :: matin(matdim, matdim)
complex(dp), intent(out) :: matout(matdim, matdim)
real(dp), intent(out) :: mateigval(matdim)
complex(dp), allocatable :: work(:)
real(dp), allocatable :: rwork(:)
integer, allocatable :: iwork(:)
!-----------------
lda0 = matdim
lwmax0 = 2 * matdim + matdim**2
allocate(work(lwmax0))
allocate(rwork(1 + 5 * matdim + 2 * matdim**2))
allocate(iwork(3 + 5 * matdim))
matout = matin
lwork = -1
liwork = -1
lrwork = -1
! 初次调用 zheevd 获取最佳工作空间大小
call zheevd('V', 'U', matdim, matout, lda0, mateigval, work, lwork, rwork, lrwork, iwork, liwork, info)
! 根据第一次调用的返回值重新调整工作空间大小
lwork = min(2 * matdim + matdim**2, int(work(1)))
lrwork = min(1 + 5 * matdim + 2 * matdim**2, int(rwork(1)))
liwork = min(3 + 5 * matdim, iwork(1))
! 重新分配工作空间
deallocate(work)
allocate(work(lwork))
deallocate(rwork)
allocate(rwork(lrwork))
deallocate(iwork)
allocate(iwork(liwork))
! 第二次调用 zheevd 计算本征值和本征矢量
call zheevd('V', 'U', matdim, matout, lda0, mateigval, work, lwork, rwork, lrwork, iwork, liwork, info)
! 错误处理
if (info > 0) then
open(11, file = "mes.dat", status = "unknown")
write(11, *) 'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine diagonalize_Hermitian_matrix
绘图代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
import matplotlib.gridspec as gridspec
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#----------------------------------------------------------
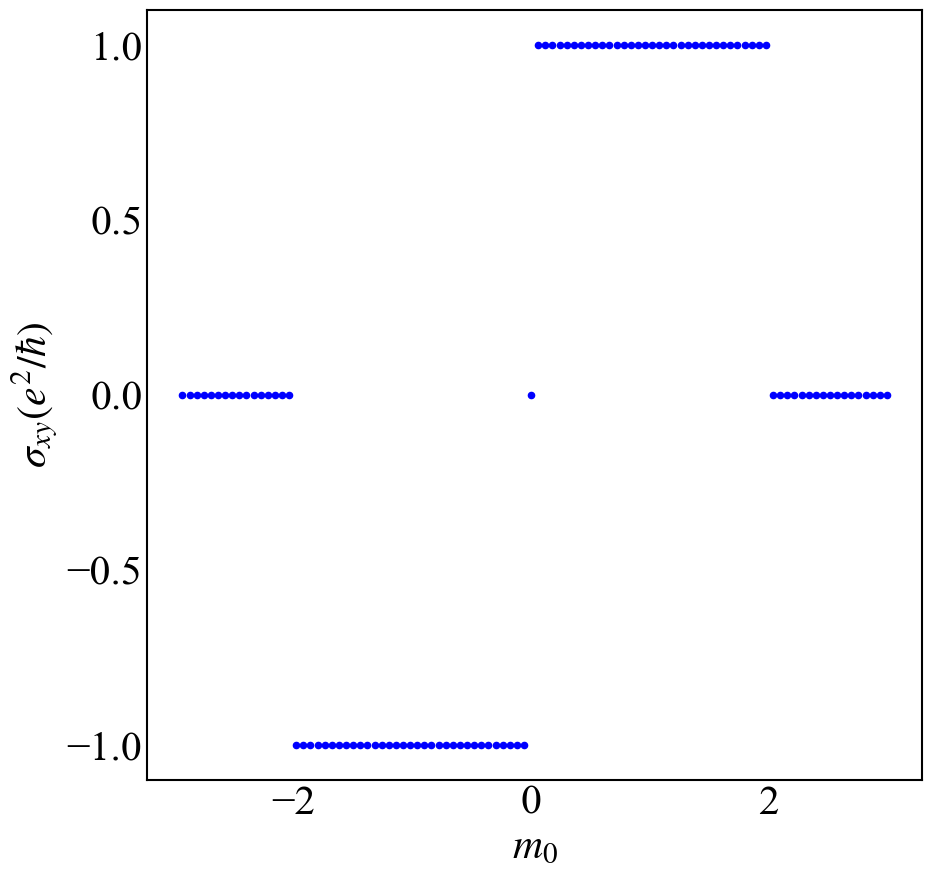
def plot_hall():
dataname = "Hall-mu.dat"
picname = os.path.splitext(dataname)[0] + ".png"
da = np.loadtxt(dataname)
plt.figure(figsize = (10,10))
plt.scatter(da[:,0],da[:,1], s = 20,c = "b")
plt.xlabel(r"$m_0$")
plt.ylabel(r"$\sigma_{xy}(e^2/\hbar)$")
# plt.xlim(0,Umax)
plt.tick_params(direction = 'in' ,axis = 'x',width = 0,length = 10)
plt.tick_params(direction = 'in' ,axis = 'y',width = 0,length = 10)
# plt.axis('scaled')
ax = plt.gca()
ax.locator_params(axis='x', nbins = 5) # x 轴最多显示 3 个刻度
ax.locator_params(axis='y', nbins = 5) # y 轴最多显示 3 个刻度
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
# plt.show()
plt.savefig(picname, dpi = 100,bbox_inches = 'tight')
plt.close()
#------------------------------------------------------------
if __name__=="__main__":
plot_hall()
所有文件可以点击这里下载.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |