整理用Fortran读取Wannier90拟合的hr数据,后续设计到极化率以及响应之类的计算还是用Fortran的计算速度是最快的。
前言
在之前博客利用Wannier90的hr数据构建动量空间能带并计算高对称点宇称中用Python实现过读取Wannier90_hr.dat这个数据,当时只是涉及到计算一下能带以及拓扑不变量,此时不会遇到一些计算瓶颈。在涉及到一些响应系数或者RPA极化率计算 的时候Python用起来就有点慢了,所以干脆也就用Fortran写一个读取Wannier90_hr.dat的程序,方面以后自己使用。
代码
module param
implicit none
integer,parameter::dp = kind(1.0)
integer numk_bz,num_wann,nrpts,numk_FS,kn
real(dp) mu
parameter(kn = 100,mu = 0.0)
real(dp),parameter::pi = 3.1415926535897
real(dp),parameter::deltaE = 0.01 ! 费米面展宽
complex(dp),parameter::im = (0.,1.) !Imagine unit
real(dp),allocatable::ones_ham(:,:) ! 为了后续考虑化学势
complex(dp),allocatable::HmnR(:,:,:) ! hr中的hopping
integer,allocatable::irvec(:,:) ! hr中的位置矢量
integer,allocatable::indorbit(:,:,:,:)
real(dp),allocatable::BZklist(:,:)
real(dp),allocatable::FS_points(:,:)
integer FS_index(-kn:kn - 1,-kn:kn - 1)
!------------------------------------------
integer,allocatable::FSindex(:,:) ! 费米点索引指标
end module
!==============================================================================================================================================================
program main
use param
use mpi
implicit none
integer numcore,indcore,ierr
!-------------------------------------------------
real(dp) code_time_start,code_time_end,code_time
integer nki,nkf
character(len = 20)::filename,char1,char2,char3,char4
!-------------------------------------------------------------------
call MPI_INIT(ierr) ! 初始化进程
call MPI_COMM_RANK(MPI_COMM_WORLD, indcore, ierr) ! 得到本进程在通信空间中的rank值,即在组中的逻辑编号(该indcore为0到numcore-1间的整数,相当于进程的ID。)
call MPI_COMM_SIZE(MPI_COMM_WORLD, numcore, ierr) !获得进程数量,用numcoer保存
! 循环分拆
nki = floor(indcore * (2.0 * kn)/numcore) - kn
nkf = floor((indcore + 1) * (2.0 * kn)/numcore) - kn - 1
if(indcore.eq.0)then
call CPU_TIME(code_time_start)
write(*,*)"Start calcation: ",code_time_start
write(*,*)"Number of CPU = ",numcore
write(*,*)"Number of nk = ",2 * kn
end if
! 输出程序的基本参数信息
if(indcore.eq.0)then
write(*,*)"Number of Fermi points = ",numk_FS
write(*,*)"Number of BZ points = ",numk_bz
call squareBZ()
call read_hr()
call fermisurface() ! 确定体系的费米面,其中会给出所有费米点的位置
call CPU_TIME(code_time_end)
write(*,*)"Calcation finished",code_time_end
write(*,*)"Code execution time:",abs(code_time_end - code_time_start),"second"
end if
call MPI_Finalize(ierr)
stop
end program main
!================================================================================================================================================================================================
subroutine fermisurface()
use param
integer ibz,ie,ikx,iky
real(dp) kx,ky,mateigval(num_wann)
complex(dp) Ham_temp(num_wann,num_wann),matvec(num_wann,num_wann)
! call honeycomyBZ()
open(13,file = "FS.dat")
! numk_FS = 0 ! 全局变量,共计费米点的数量
do ibz = 1,numk_bz
kx = BZklist(1,ibz)
ky = BZklist(2,ibz)
call HamR_to_K(kx,ky,0.0,Ham_temp)
call diagonalize_Hermitian_matrix(num_wann,Ham_temp,matvec,mateigval)
do ie = 1,num_wann
if (abs(mateigval(ie)) < deltaE)then
write(13,"(3F12.6)")kx,ky,1.0
numk_FS = numk_FS + 1 ! 统计费米点的数量
end if
end do
end do
close(13)
!--------------------------------------------------------------
!确定费米面点的数量后就可以确定相互作用矩阵的维度
if(numk_FS.eq.0)then
write(*,*)"The Number of Fermi surface points = ",numk_FS
write(*,*)"----------------------------------------------"
write(*,*)" Warnning "
write(*,*)"----------------------------------------------"
stop
else
allocate(FS_points(2,numk_FS))
FS_points = 0.0
end if
!-----------------------------------------------
! 根据动量坐标记录这是第几个费米点
numk_FS = 0
do iky = -kn,kn - 1
ky = 2.0 * pi * iky/kn
do ikx = -kn,kn - 1
kx = 2.0 * pi * ikx/kn
call HamR_to_K(kx,ky,0.0,Ham_temp)
call diagonalize_Hermitian_matrix(num_wann,Ham_temp,matvec,mateigval)
do ie = 1,num_wann
if (abs(mateigval(ie)) < deltaE)then
numk_FS = numk_FS + 1
FS_index(ikx,iky) = numk_FS
FS_points(1,numk_FS) = kx
FS_points(2,numk_FS) = ky
end if
end do
end do
end do
return
end subroutine
!================================================================================================================================================================================================
subroutine squareBZ()
use param
integer ikx,iky,i0
! 对于四方点阵,BZ的点数可以直接确定
numk_bz = (2 * kn)**2
allocate(BZklist(2,numk_bz))
i0 = 0
do ikx = -kn,kn - 1
do iky = -kn,kn - 1
i0 = i0 + 1
BZklist(1,i0) = 2.0 * pi * ikx/kn
BZklist(2,i0) = 2.0 * pi * iky/kn
end do
end do
return
end subroutine
!==============================================================================================================================================================
subroutine HamR_to_K(kx,ky,kz,Ham_temp)
! 将hr变成动量空间
use param
implicit none
real(dp) kx,ky,kz
integer i1,i2,i3,w1,w2,r1,r2,r3
complex(dp) Ham_temp(num_wann,num_wann)
ones_ham = 0.0 ! 对于具有allocatable属性的变量,一定要先赋值为零
! 设置单位矩阵
do i1 = 1,num_wann
ones_ham(i1,i1) = 1.0
end do
Ham_temp = 0.0
do i1 = 1,nrpts
do i2 = 1,num_wann
do i3 = 1,num_wann
r1 = irvec(1,i1)
r2 = irvec(2,i1)
r3 = irvec(3,i1)
w1 = indorbit(1,i1,i2,i3)
w2 = indorbit(2,i1,i2,i3)
Ham_temp(w1,w2) = Ham_temp(w1,w2) + (cos(kx * r1 + ky * r2 + kz * r3) + im * sin(kx * r1 + ky * r2 + kz * r3)) * HmnR(w1,w2,i1)
end do
end do
end do
Ham_temp = Ham_temp - mu * ones_ham ! 在Wannier90_hr的基础上考虑体系的化学势
end subroutine
!==============================================================================================================================================================
subroutine read_hr()
! 读取DFT的hr数据,并返回Hr以及
use param
implicit none
integer :: i,j,k
integer :: r1,r2,r3,w1,w2
real(dp) :: hr,hi
real(dp),allocatable::ndegen(:)
logical stat
inquire(file = 'wannier90_hr.dat', exist = stat)
if(stat)then
open(12,file = 'wannier90_hr.dat',action = 'read')
read(12,*)
read(12,*) num_wann ! 轨道数量,也决定了动量空间哈密顿量维度,这是一个全局变量
! read(12,*)r1
read(12,*) nrpts
allocate(ndegen(nrpts))
! 全局变量
allocate(HmnR(num_wann,num_wann,nrpts),irvec(3,nrpts))
allocate(indorbit(2,nrpts,num_wann,num_wann))
read(12,*) (ndegen(i),i = 1,nrpts)
do i = 1,nrpts
do j = 1,num_wann
do k = 1,num_wann
read(12,*) r1,r2,r3,w1,w2,hr,hi
irvec(1,i) = r1
irvec(2,i) = r2
irvec(3,i) = r3
indorbit(1,i,j,k) = w1 ! 哈密顿量中的轨道索引,后续构建动量空间哈密顿量使用
indorbit(2,i,j,k) = w2
HmnR(w1,w2,i) = hr + im * hi
enddo
end do
end do
close(12)
allocate(ones_ham(num_wann,num_wann))
else
write(*,*)"**************** Error *********************"
write(*,*)"Tight-binding dat is not exist"
write(*,*)"**************** Error *********************"
end if
return
end subroutine read_hr
!==============================================================================================================================================================
function delta(x)
!> Lorentz or gaussian expansion of the Delta function
use param, only : dp, pi
implicit none
! real(dp), intent(in) :: eta
real(dp), intent(in) :: x
real(dp) :: delta, y
real(dp) :: eta = 0.001
!> Lorentz expansion
!delta= 1d0/pi*eta/(eta*eta+x*x)
y= x*x/eta/eta/2d0
!> Gaussian broadening
!> exp(-60) = 8.75651076269652e-27
if (y>60d0) then
delta = 0d0
else
delta= exp(-y)/sqrt(2d0*pi)/eta
endif
return
end function delta
!==============================================================================================================================================================
subroutine diagonalize_complex_matrix(matdim,matin,matout,mateigval)
! 对角化一般复数矩阵,这里的本征值是个复数
! matin 输入矩阵 matout 本征矢量 mateigval 本征值
implicit none
integer,parameter::dp = kind(1.0)
integer matdim,LDA,LDVL,LDVR,LWMAX,INFO,LWORK
complex(dp),intent(in)::matin(matdim,matdim)
complex(dp),intent(out)::matout(matdim,matdim)
complex(dp),intent(out)::mateigval(matdim)
real(dp),allocatable::RWORK(:)
complex(dp),allocatable::WORK(:)
complex(dp),allocatable::VL(:,:)
complex(dp),allocatable::VR(:,:)
LDA = matdim
LDVL = matdim
LDVR = matdim
LWMAX = 2 * matdim + matdim**2
! write(*,*)matin
allocate(RWORK(2 * matdim))
allocate(VL(LDVL,matdim))
allocate(VR(LDVR, matdim))
allocate(WORK(LWMAX))
matout = matin
LWORK = -1
call cgeev( 'V', 'N', matdim, matout, LDA, mateigval, VL, LDVL,VR, LDVR, WORK, LWORK, RWORK, INFO)
LWORK = MIN( LWMAX, INT( WORK( 1 ) ) )
call cgeev( 'V', 'N', matdim, matout, LDA, mateigval, VL, LDVL,VR, LDVR, WORK, LWORK, RWORK, INFO )
IF( INFO.GT.0 ) THEN
WRITE(*,*)'The algorithm failed to compute eigenvalues.'
! STOP
END IF
end subroutine diagonalize_complex_matrix
!================================================================================================================================================================================================
subroutine Matrix_Inv(matdim,matin,matout)
! 矩阵求逆
implicit none
integer,parameter::dp = kind(1.0)
integer matdim,info
complex(dp),intent(in) :: matin(matdim,matdim)
complex(dp):: matout(size(matin,1),size(matin,2))
real(dp):: work2(size(matin,1)) ! work2 array for LAPACK
integer::ipiv(size(matin,1)) ! pivot indices
! Store matin in matout to prevent it from being overwritten by LAPACK
matout = matin
! SGETRF computes an LU factorization of a general M - by - N matrix A
! using partial pivoting with row interchanges .
call CGETRF(matdim,matdim,matout,matdim,ipiv,info)
! if (info.ne.0) stop 'Matrix is numerically singular!'
if (info.ne.0) write(*,*)'Matrix is numerically singular!'
! SGETRI computes the inverse of a matrix using the LU factorization
! computed by SGETRF.
call CGETRI(matdim,matout,matdim,ipiv,work2,matdim,info)
! if (info.ne.0) stop 'Matrix inversion failed!'
if (info.ne.0) write(*,*)'Matrix inversion failed!'
return
end subroutine Matrix_Inv
!================================================================================================================================================================================================
subroutine diagonalize_Hermitian_matrix(matdim,matin,matout,mateigval)
! 厄米矩阵对角化
! matin 输入矩阵 matout 本征矢量 mateigval 本征值
implicit none
integer,parameter::dp = kind(1.0)
integer matdim
integer lda0,lwmax0,lwork,lrwork,liwork,info
complex(dp) matin(matdim,matdim),matout(matdim,matdim)
real(dp) mateigval(matdim)
complex(dp),allocatable::work(:)
real(dp),allocatable::rwork(:)
integer,allocatable::iwork(:)
!-----------------
lda0 = matdim
lwmax0 = 2 * matdim + matdim**2
allocate(work(lwmax0))
allocate(rwork(1 + 5 * matdim + 2 * matdim**2))
allocate(iwork(3 + 5 * matdim))
matout = matin
lwork = -1
liwork = -1
lrwork = -1
call cheevd('V','U',matdim,matout,lda0,mateigval,work,lwork ,rwork,lrwork,iwork,liwork,info)
lwork = min(2 * matdim + matdim**2, int( work( 1 ) ) )
lrwork = min(1 + 5 * matdim + 2 * matdim**2, int( rwork( 1 ) ) )
liwork = min(3 + 5 * matdim, iwork( 1 ) )
call cheevd('V','U',matdim,matout,lda0,mateigval,work,lwork,rwork,lrwork,iwork,liwork,info)
if( info .GT. 0 ) then
open(11,file = "mes.dat",status = "unknown")
write(11,*)'The algorithm failed to compute eigenvalues.'
close(11)
end if
return
end subroutine diagonalize_Hermitian_matrix
绘图程序
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import matplotlib.cm as cm
import os
import re
plt.rc('font', family='Times New Roman')
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#----------------------------------------------------------------------------
def WannierDETband():
path = os.path.abspath('.')
band_file = os.path.join(path,'BAND.dat')
knode_file = os.path.join(path,'KLABELS')
fermi_file = os.path.join(path,'FERMI_ENERGY')
plt.figure(figsize = (10,8))
#******************** DFT band ************************************************************
band_data = np.loadtxt(band_file)
plt.plot(band_data[:,0],band_data[:,1:],color = 'b',linewidth = 2.0,label = "DFT")
xmin = np.min(band_data[:,0])
xmax = np.max(band_data[:,0])
ymin = np.min(band_data[:,1:])
ymax = np.max(band_data[:,1:])
plt.xlim(xmin,xmax)
# plt.ylim(ymin,ymax)
plt.ylim(-6,6)
with open(knode_file,"r",encoding = "utf-8") as f:
lines = f.readlines()
lines = lines[1:-3]
knodes = []
for i in range(len(lines)):
knodes.append(str.split(lines[i]))
knodes[i][1] = float(knodes[i][1])
plt.axvline(x = knodes[i][1],linewidth = 1.5,color = 'silver')
plt.axhline(y = 0,linewidth = 2.0,color = 'b',ls = "-.")
knodes = list(map(list, zip(*knodes)))
plt.xticks(knodes[1],list(knodes[0]),fontproperties='Times New Roman')
#******************** Wannier band ********************
wannier_bandfile = os.path.join(path,'wannier90_band.dat')
wannier_kptfile = os.path.join(path,'wannier90_band.kpt')
wannier_labkptfile = os.path.join(path,'wannier90_band.labelinfo.dat')
fermi_file = os.path.join(path,'FERMI_ENERGY')
wannier_print = True
if os.path.exists(wannier_bandfile) is True and wannier_print is True:
wann_k = open(wannier_kptfile,"r",encoding = "utf-8")
wann_l = open(wannier_labkptfile,"r",encoding = "utf-8")
n_k = np.array(int(wann_k.readlines()[0]))
lab = np.array(re.findall('[A-Z]*[A-Z]',wann_l.read()))
fermi_energy = np.loadtxt(fermi_file)
wann_k.close()
wann_l.close()
wb = np.loadtxt(wannier_bandfile)
wj = int(len(wb)/n_k)
for j in range(wj):
if j == wj - 2:
plt.plot(wb[:,0][j*n_k:j*n_k+n_k],wb[:,1][j*n_k:j*n_k+n_k] - fermi_energy,color = 'r',ls = '--',linewidth = 2.0,label = "Wannier")
else:
plt.plot(wb[:,0][j*n_k:j*n_k+n_k],wb[:,1][j*n_k:j*n_k+n_k] - fermi_energy,color = 'r',ls = '--',linewidth = 2.0)
plt.legend(loc='upper right', shadow = True, fancybox = True)
#********************************************************************************
plt.tick_params(axis='x',width = 0,length = 10)
plt.tick_params(axis='y',width = 0,length = 10)
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
# plt.show()
plt.savefig("bandstructure.png",dpi = 300,bbox_inches = 'tight',transparent=True)
#-----------------------------------------------------------------------------------------------------
def plotfs(mu,numk):
# 费米面以及极化率绘制
dataname = "fermi-mu-" + str(mu) + "-numk-" + str(numk) + ".dat"
dataname = "FS.dat"
# dataname = "Honeycomb-fermi-mu-" + str(mu) + ".dat"
# dataname = "Square-fermi-mu-" + str(mu) + ".dat"
# dataname = "fermi-mu-" + str(mu) + ".dat"
# dataname = "Honeycomb-fermivs-" + str(mu) + ".dat"
# dataname = "maxvals-chi0-" + str(numk) + ".dat"
# picname = os.path.splitext(dataname)[0] + "-" + str(num) + ".png"
picname = os.path.splitext(dataname)[0] + ".png"
da = np.loadtxt(dataname)
plt.figure(figsize = (10,8))
sc = plt.scatter(da[:,0],da[:,1], s = 1, c = da[:,2],cmap = "jet")
#-------------------------------------------------
r0 = 5
hex = [np.sqrt(3)/2 * r0,np.sqrt(3)/4 * r0,-np.sqrt(3)/4 * r0,-np.sqrt(3)/2 * r0,-np.sqrt(3)/4 * r0,np.sqrt(3)/4 * r0,np.sqrt(3)/2 * r0]
hey = [0 * r0 ,3/4 * r0 ,3/4 * r0 ,0 * r0 ,-3/4 * r0 ,-3/4 * r0 ,0 * r0]
plt.plot(hex,hey,c = "black",lw = 2,ls = "--")
#-------------------------------------------------
cb = plt.colorbar(sc,fraction = 0.1,ticks = [np.min(da[:,2]),np.max(da[:,2])]) # 调整colorbar的大小和图之间的间距
# cb.ax.set_yticklabels([r'$d_{3z^2-r^2}$', r'$d_{x^2-y^2}$'])
xtic = [-2 * np.pi,0,2 * np.pi]
xticlab = ["$-2\pi$","$0$","$2\pi$"]
plt.xticks(xtic,list(xticlab),fontproperties='Times New Roman', size = 40)
plt.yticks(xtic,list(xticlab),fontproperties='Times New Roman', size = 40)
xmin = np.min(da[:,0])
xmax = np.max(da[:,0])
ymin = np.min(da[:,1])
ymax = np.max(da[:,1])
# plt.xlim(xmin,xmax)
# plt.ylim(ymin,ymax)
plt.xlim(-2 * np.pi,2 * np.pi)
plt.ylim(-2 * np.pi,2 * np.pi)
plt.tick_params(axis='x',width = 0,length = 10)
plt.tick_params(axis='y',width = 0,length = 10)
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
# plt.show()
plt.savefig(picname, dpi = 300,bbox_inches = 'tight',transparent=True)
plt.close()
#-----------------------------------------------------------------------------------------------------
# WannierDETband()
numk = 100
mu = -2.15
plotfs(format(mu,".2f"),format(numk,".2f"))
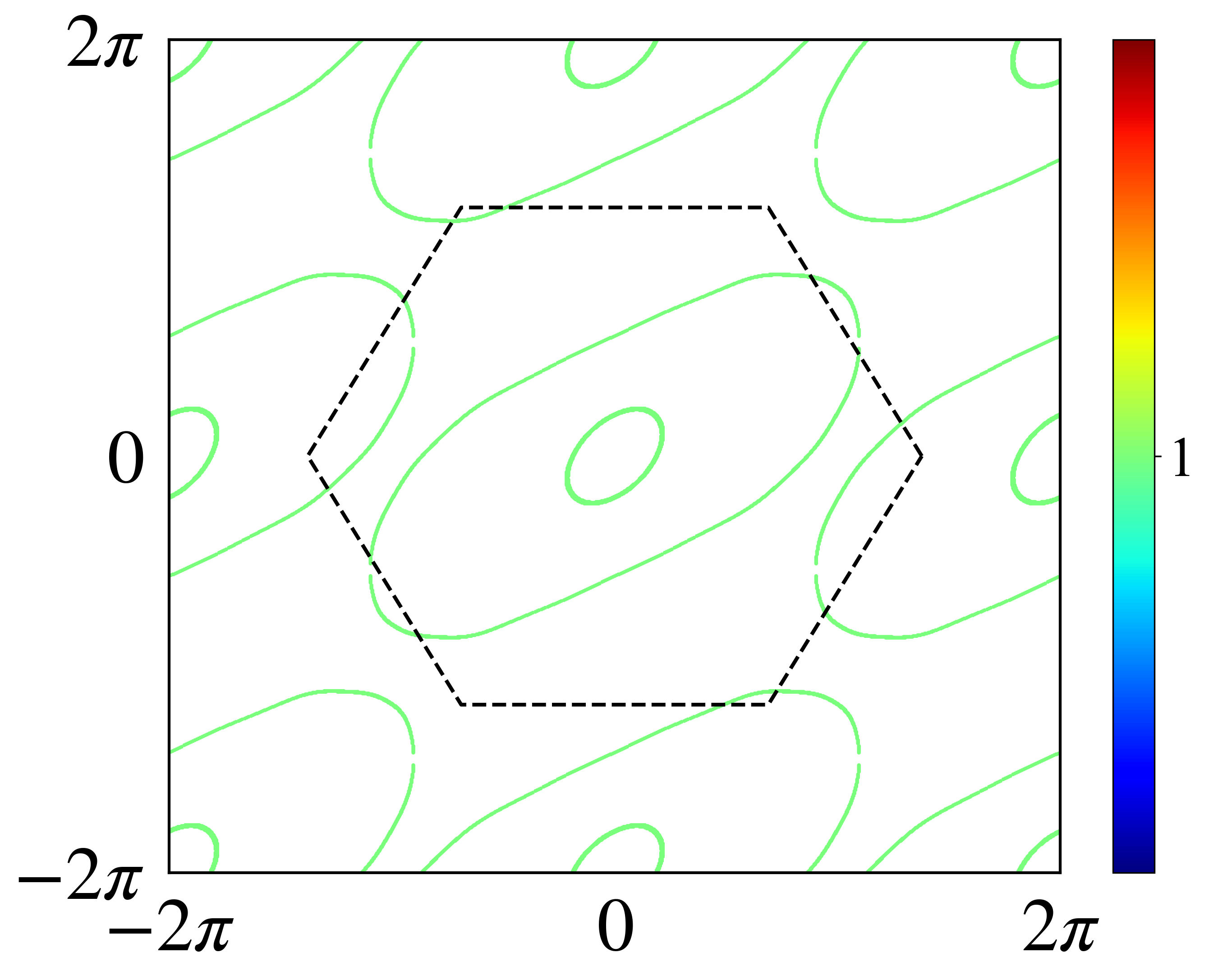
上面的所有文件可以点击这里下载
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |