这里想整理一下如何利用已有的实空间的tight binding的数据,通过Fourier变换来得到动量空间中的模型,从而可以利用同时利用这两种不同表象下的数据进行计算研究。这里使用了BHZ模型作为例子来进行研究,并利用Fu-Kane判据计算了高对称点的宇称,从而达到计算拓扑不变量的目的。
前言
之前已经学习了如何将一个现有的动量空间中的模型,变换成Wannier90所输出的tight binding的数据,可以参考从紧束缚模型出发构建WannierTools需要的数据这个Blog中的内容,因为现有一些程序是可以直接利用这些数据进行计算的,但是同样有时候需要利用实空间的tight binding数据来进行动量空间中的一些计算,这里就想整理一个比较通用的脚本,可以方便的将一个Wannier90输出的TB模型的数据,通过Fourier变换从而来得到动量空间中的哈密顿量,这样可以方便自己进行后面的一些计算.
数据结构分析
这里就以最熟悉的BHZ模型为例,借用从紧束缚模型出发构建WannierTools需要的数据这篇Blog中的方法,来构建
\[H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+ A_x\sin k_x\sigma_xs_z+A\sin k_y\sigma_y\]这个哈密顿量的wannier90_hr.dat这个数据,程序如下
! Quantum Spin Hall
! usage:
! compile and run
! gfortran hr_bhz.f90 -o hr_bhz
! ./hr_bhz
! H = Ax sin(kx)sigma_x s_z + Ay sin(ky) sigma_y s_0 + (m0 - tx cos(kx) - ty cos(ky))sigma_z s_0 + lam1 sigma_0 s_x
program hr_bhz
implicit none
integer, parameter :: dp=kind(1d0) ! 双精度计算
complex(dp), parameter :: im = (0d0, 1d0) ! 虚数单位i
complex(dp), parameter :: zzero = (0d0, 0d0)
integer :: i, j
integer :: ir
integer :: nwann
!> arrays for hamiltonian storage
integer :: nrpts
integer, allocatable :: ndegen(:)
integer, allocatable :: irvec(:, :)
complex(dp), allocatable :: hmnr(:, :, :)
!> three lattice constants
real(dp) :: Ax,Ay,m0,tx,ty,lamc
Ax = 1d0
Ay = 1d0
m0 = 1.5d0
tx = 1d0
ty = 1d0
lamc = 0.2d0 ! 层间耦合大小
nwann = 2 ! 构建紧束缚模型时候Wannier轨道的数目,这个模型中有4个轨道,化学式为零时占据两个
nrpts = 17
allocate(irvec(3, nrpts)) ! 该模型时2D的,所以hopping的方向也就只有2个,所以在之后的设置中保持第三个方向上恒为0
allocate(ndegen(nrpts))
allocate(hmnr(nwann*2, nwann*2, nrpts))
irvec = 0
ndegen = 1 ! 手动设置紧束缚模型数据所需要
hmnr = zzero ! 矩阵初始化
! 0 0 onsite能量
ir = 1 ! ir用来记录这里一共会有多少个hopping的方位(包括了onsite)
irvec(1, ir) = 0
irvec(2, ir) = 0
hmnr(1, 1, ir) = m0
hmnr(2, 2, ir) = m0
hmnr(3, 3, ir) = -m0
hmnr(4, 4, ir) = -m0
hmnr(1 ,2, ir) = lamc
hmnr(2 ,1, ir) = lamc
hmnr(3 ,4, ir) = lamc
hmnr(4 ,3, ir) = lamc
!1 0 x正反向hopping
ir = ir + 1
irvec(1, ir) = 1
irvec(2, ir) = 0
hmnr(1, 1, ir) = tx/2.0
hmnr(2, 2, ir) = tx/2.0
hmnr(3, 3, ir) = -tx/2.0
hmnr(4, 4, ir) = -tx/2.0
hmnr(1, 3, ir) = ax/(2.0*im)
hmnr(2, 4, ir) = -ax/(2.0*im)
hmnr(3, 1, ir) = ax/(2.0*im)
hmnr(4, 2, ir) = -ax/(2.0*im)
!-1 0 x负方向hopping
ir = ir+ 1
irvec(1, ir) = -1
irvec(2, ir) = 0
hmnr(1, 1, ir) = tx/2.0
hmnr(2, 2, ir) = tx/2.0
hmnr(3, 3, ir) = -tx/2.0
hmnr(4, 4, ir) = -tx/2.0
hmnr(1, 3, ir) = -ax/(2.0*im)
hmnr(2, 4, ir) = ax/(2.0*im)
hmnr(3, 1, ir) = -ax/(2.0*im)
hmnr(4, 2, ir) = ax/(2.0*im)
! 0 1 y正方向hopping
ir = ir + 1
irvec(1, ir) = 0
irvec(2, ir) = 1
hmnr(1, 1, ir) = ty/2.0
hmnr(2, 2, ir) = ty/2.0
hmnr(3, 3, ir) = -ty/2.0
hmnr(4, 4, ir) = -ty/2.0
hmnr(1, 3, ir) = -im*ay/(2.0*im)
hmnr(2, 4, ir) = -im*ay/(2.0*im)
hmnr(3, 1, ir) = im*ay/(2.0*im)
hmnr(4, 2, ir) = im*ay/(2.0*im)
!0 -1 y负方向hopping
ir = ir + 1
irvec(1, ir) = 0
irvec(2, ir) = -1
hmnr(1, 1, ir) = ty/2.0
hmnr(2, 2, ir) = ty/2.0
hmnr(3, 3, ir) = -ty/2.0
hmnr(4, 4, ir) = -ty/2.0
hmnr(1, 3, ir) = im*ay/(2.0*im)
hmnr(2, 4, ir) = im*ay/(2.0*im)
hmnr(3, 1, ir) = -im*ay/(2.0*im)
hmnr(4, 2, ir) = -im*ay/(2.0*im)
nrpts = ir
!> write to new_hr.dat
open(unit=105, file='wannier90_hr.dat')
write(105, *)'BHZ model'
write(105, *)nwann*2
write(105, *)nrpts
write(105, '(15I5)')(ndegen(i), i=1, nrpts)
do ir = 1, nrpts
do i = 1, nwann*2
do j = 1, nwann*2
write(105, '(5I5, 2f16.8)')irvec(:, ir), i, j, HmnR(i, j, ir)
end do
end do
end do
close(105)
stop
end ! end of program
先来看看数据结构
- 第一行
注释,说明一下这个TB数据是什么体系的
- 第二行
能带数目,从模型的角度可以理解成哈密顿量的维度,多大的矩阵自然就对应几条能带,但是可能包含简并,简并度是多少就算多少条能带.
- 第三行
在实空间中,每个格点上的hopping的方向,比如$\cos k_x=\frac{1}{2}(e^{ik_x\cdot R_x}+e^{-ik_x\cdot R_x})\quad R_x=1$,这里假设晶格长度为单位1,所以此时就是有两个hopping的方向,同样的格点上的onsite占位能也同样算是一个方向,比如在BHZ模型中$m_0$就代表的是格点上的占位能,它同样也是一个方向,所以BHZ中x的正负方向,以及y的正负方向,还有onsite能量,就一共存在5个hopping的方向,这也就是第三行的含义.
- 第四行
这一行是每个hopping方向格点上的简并度,因为这里研究的是BHZ模型,TB数据是手动构造的,所以这个数字都是1,这里由多少个hopping方向就会存在所少个数字.
- 第五行及之后
\(\begin{equation}
x\quad y\quad z\quad m\quad n\quad\text{Re}\quad\text{Im}
\end{equation}\)
这里前面的三个数(x,y,z)就是用来定义实空间中hopping的方向,比如x正方向最近邻hopping为$(1,0,0)$,其他更远或者其他方向的hopping就可以通过类似的方式来得到.后面的$(m,n)$表示的是能带指标,而最后两行代表的是hopping对应的实部和虚部.关于数据结构这部分的内容,同样可以参考WannierTools中的解释.
BHZ model 4 5 1 1 1 1 1 0 0 0 1 1 1.50000000 0.00000000 0 0 0 1 2 0.20000000 0.00000000 0 0 0 1 3 0.00000000 0.00000000 0 0 0 1 4 0.00000000 0.00000000 0 0 0 2 1 0.20000000 0.00000000 0 0 0 2 2 1.50000000 0.00000000 0 0 0 2 3 0.00000000 0.00000000 0 0 0 2 4 0.00000000 0.00000000 0 0 0 3 1 0.00000000 0.00000000 0 0 0 3 2 0.00000000 0.00000000 0 0 0 3 3 -1.50000000 0.00000000 0 0 0 3 4 0.20000000 0.00000000 0 0 0 4 1 0.00000000 0.00000000 0 0 0 4 2 0.00000000 0.00000000 0 0 0 4 3 0.20000000 0.00000000 0 0 0 4 4 -1.50000000 0.00000000 1 0 0 1 1 0.50000000 0.00000000 1 0 0 1 2 0.00000000 0.00000000 1 0 0 1 3 0.00000000 -0.50000000 1 0 0 1 4 0.00000000 0.00000000 1 0 0 2 1 0.00000000 0.00000000 1 0 0 2 2 0.50000000 0.00000000 1 0 0 2 3 0.00000000 0.00000000 1 0 0 2 4 0.00000000 0.50000000 1 0 0 3 1 0.00000000 -0.50000000 1 0 0 3 2 0.00000000 0.00000000 1 0 0 3 3 -0.50000000 0.00000000 1 0 0 3 4 0.00000000 0.00000000 1 0 0 4 1 0.00000000 0.00000000 1 0 0 4 2 0.00000000 0.50000000 1 0 0 4 3 0.00000000 0.00000000 1 0 0 4 4 -0.50000000 0.00000000 -1 0 0 1 1 0.50000000 0.00000000 -1 0 0 1 2 0.00000000 0.00000000 -1 0 0 1 3 0.00000000 0.50000000 -1 0 0 1 4 0.00000000 0.00000000 -1 0 0 2 1 0.00000000 0.00000000 -1 0 0 2 2 0.50000000 0.00000000 -1 0 0 2 3 0.00000000 0.00000000 -1 0 0 2 4 0.00000000 -0.50000000 -1 0 0 3 1 0.00000000 0.50000000 -1 0 0 3 2 0.00000000 0.00000000 -1 0 0 3 3 -0.50000000 0.00000000 -1 0 0 3 4 0.00000000 0.00000000 -1 0 0 4 1 0.00000000 0.00000000 -1 0 0 4 2 0.00000000 -0.50000000 -1 0 0 4 3 0.00000000 0.00000000 -1 0 0 4 4 -0.50000000 0.00000000 0 1 0 1 1 0.50000000 0.00000000 0 1 0 1 2 0.00000000 0.00000000 0 1 0 1 3 -0.50000000 0.00000000 0 1 0 1 4 0.00000000 0.00000000 0 1 0 2 1 0.00000000 0.00000000 0 1 0 2 2 0.50000000 0.00000000 0 1 0 2 3 0.00000000 0.00000000 0 1 0 2 4 -0.50000000 0.00000000 0 1 0 3 1 0.50000000 0.00000000 0 1 0 3 2 0.00000000 0.00000000 0 1 0 3 3 -0.50000000 0.00000000 0 1 0 3 4 0.00000000 0.00000000 0 1 0 4 1 0.00000000 0.00000000 0 1 0 4 2 0.50000000 0.00000000 0 1 0 4 3 0.00000000 0.00000000 0 1 0 4 4 -0.50000000 0.00000000 0 -1 0 1 1 0.50000000 0.00000000 0 -1 0 1 2 0.00000000 0.00000000 0 -1 0 1 3 0.50000000 0.00000000 0 -1 0 1 4 0.00000000 0.00000000 0 -1 0 2 1 0.00000000 0.00000000 0 -1 0 2 2 0.50000000 0.00000000 0 -1 0 2 3 0.00000000 0.00000000 0 -1 0 2 4 0.50000000 0.00000000 0 -1 0 3 1 -0.50000000 0.00000000 0 -1 0 3 2 0.00000000 0.00000000 0 -1 0 3 3 -0.50000000 0.00000000 0 -1 0 3 4 0.00000000 0.00000000 0 -1 0 4 1 0.00000000 0.00000000 0 -1 0 4 2 -0.50000000 0.00000000 0 -1 0 4 3 0.00000000 0.00000000 0 -1 0 4 4 -0.50000000 0.00000000
文件读写
import numpy as np
import matplotlib.pyplot as plt
# ------------------------------------
file = open('wannier90_hr.dat') # 打开TB模型的数据
comment = file.readline()
Band_number = int(file.readline())
Hopping_number = int(file.readline()) # 对于单独的一个字符串可以将其转化为整数
degenerate = [] # 用来存储每个hopping的简并度,每个hopping方向对应一个数字
con = 0
for line in file: # 接着上面读取到行的位置继续读
temp = line.strip().split() # 移除字符串头尾指定的字符(默认为空格),并以空格将这些字符串分开
t1 = [int(x) for x in temp] #遍历每个字符串并转换为整数
degenerate.extend(t1) # 数据追加
if len(degenerate) == Hopping_number: # 当获取的hopping对应的简并度的个数和hopping方向的数目相等的时候,就停止读取文件
break
# 接下来读取核心的hr参数,也就是不同带之间hopping的大小以及方向,hr文件中剩下所有的数据都是这些信息,因此可以直接读取到文件末尾
Hr = []
for line in file:
temp = line.strip().split() # 先除去空格,再以空格分立成单独的字符串
# 将所有的字符串再转化成数值进行存储
Hr.append([int(temp[0]),int(temp[1]),int(temp[2]),int(temp[3]),int(temp[4]),float(temp[5]),float(temp[6])])
file.close() # 读取完成之后关闭文件
Hr1 = np.array(Hr) # 将一个list转化成矩阵
# 在通过TB数据进行Fourier变换得到动量空间中的模型时,需要利用的hopping R,这里将这些hopping方向R单独提取出来
Hopping_dir = np.zeros([Hopping_number,3],np.int64)
for i in range(Hopping_number):
Hopping_dir[i] = Hr1[Band_number**2 * i ,0:3] # 获取所有的hopping方向
规范一
\[\rvert\chi_i^\mathbf{k}\rangle=\sum_\mathbf{R}e^{i\mathbf{k}\cdot(\mathbf{R}-\mathbf{\tau}_i)}\rvert\phi_{\mathbf{R}i}\rangle\]利用其构建Bloch态
\[\rvert\psi_{n\mathbf{k}}\rangle=\sum_jC_{j}^{n\mathbf{k}}\rvert\chi_j^\mathbf{k}\rangle\] \[H_{ij}^\mathbf{k}=\langle\chi_i^\mathbf{k}\rvert H\rvert\chi_j^\mathbf{k}\rangle=\sum_\mathbf{R}e^{i\mathbf{k}\cdot(\mathbf{R}+\tau_j-\tau_i)}H_{ij}(\mathbf{R})\] \[H(\mathbf{k})C_{n\mathbf{k}}=E_{n\mathbf{k}}C_{n\mathbf{k}}\]这里的$ij$是轨道(能带)的索引.
规范二
\[\rvert\tilde{\chi}_i^\mathbf{k}\rangle=\sum_\mathbf{R}e^{i\mathbf{k}\cdot\mathbf{R}}\rvert\phi_{\mathbf{R}i}\rangle\]利用其构建Bloch态
\[\rvert\tilde{\psi}_{n\mathbf{k}}\rangle=\sum_j\tilde{C}_{j}^{n\mathbf{k}}\rvert\tilde{\chi}_j^\mathbf{k}\rangle\] \[\tilde{H}_{ij}^\mathbf{k}=\langle\tilde{\chi}_i^\mathbf{k}\rvert H\rvert\tilde{\chi}_j^\mathbf{k}\rangle=\sum_\mathbf{R}e^{i\mathbf{k}\cdot\mathbf{R}}H_{ij}(\mathbf{R})\]其满足的本征方程为
\[\tilde{H}(\mathbf{k})\tilde{C}_{n\mathbf{k}}=E_{n\mathbf{k}}\tilde{C}_{n\mathbf{k}}\]在同TB构建Bloch哈密顿量的时候会有两种规范选择,其实不同之处就在于构建的时候,在hopping中是否考虑轨道的中心$\tau_i$,而通过这两种规范得到的Bloch哈密顿量之间的关系为
\[\tilde{H}(\mathbf{k})_{ij}=e^{i\mathbf{k}\cdot(\tau_i-\tau_j)}H_{ij}(\mathbf{k})\]其实这个额外的位相因子通常是反映在本征矢量上的
\[\tilde{C}_j^{n\mathbf{k}}=e^{i\mathbf{k}\cdot\tau_j}C^{n\mathbf{k}}_j\]这里的n代表的是哈密顿量的那个本征值,$j$则是轨道(能带)的索引.
因为我在这里考虑的是BHZ模型,所以就直接采用第二种规范,不考虑每个轨道的$\tau_i$,主要是对于一个给出形式的Bloch哈密顿量,也确实不知道它每个给定的轨道对应的$\tau_i$是多少,但是如果是利用Wannier90计算出的hr数据(具体材料),那么在hr中就会有对应的每个轨道的$\tau_i$,这个时候就可以同时用两种不同的规范来进行Bloch哈密顿量构建.
#-------------------------------------------------------------------
def Hamk(hamhr,Hopping_dir,Hopping_number,Band_number,kx,ky):
# 同过TB数据构建动量空间哈密顿量
H = np.zeros([Band_number,Band_number],np.complex128) # 动量空间哈密顿量
for i0 in range(Hopping_number):# 对所有的R求和进行Fourier变换
H += np.exp(-1j*np.dot(Hopping_dir[i0,0:2],[kx,ky]))*hamhr[i0,:,:] # 每个轨道index对应的前面的位相因子是相同的
return H
从上面的公式中可以看到这里需要的就只是不同轨道(能带)之间的hopping大小$H_{ij}$以及hopping的方向$\mathbf{R}$,我们这里采用的是第二种规范,所以实际上就是对所有的$\mathbf{R}$求和,这里每个轨道自由度对应的这个位相因子是相同的,所以在程序中直接就使用了hamhr[i0,:,:],整个这部分用到的核心公式就是
\[H_{mn}(\mathbf{k})=\sum_\mathbf{R}e^{i\mathbf{k}\cdot\mathbf{R}}H_{mn}(\mathbf{R})\]通过上面的方式就完全由TB数据构建出了动量空间中的哈密顿量。下面就进行一下double check,验证一下高对称路径上的能带
def Band_HighSymmetry():
nx = 100
vals = []
klist = []
for i0 in range(0,nx):
kx = np.pi*i0/nx
klist.append(kx/np.pi)
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
H = Hamk(ham,Hopping_dir,Hopping_number,Band_number,kx,0)
val,vec = np.linalg.eigh(H)
vals.append(val)
for i0 in range(0,nx):
ky = np.pi*i0/nx
klist.append(1 + ky/np.pi)
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
H = Hamk(ham,Hopping_dir,Hopping_number,Band_number,np.pi,ky)
val,vec = np.linalg.eigh(H)
vals.append(val)
for i0 in range(0,nx):
ki = np.pi*i0/nx
klist.append(2 + ki/np.pi)
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
H = Hamk(ham,Hopping_dir,Hopping_number,Band_number,np.pi - ki,np.pi - ki)
val,vec = np.linalg.eigh(H)
vals.append(val)
return klist,vals
结果如下
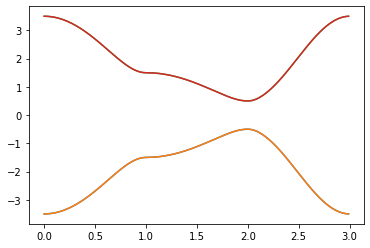
完整的代码如下
import numpy as np
import matplotlib.pyplot as plt
def Hamhr():
# ------------------------------------
file = open('wannier90_hr.dat') # 打开TB模型的数据(通常默认文件名为wannier90_hr.dat)
comment = file.readline()
Band_number = int(file.readline())
Hopping_number = int(file.readline()) # 对于单独的一个字符串可以将其转化为整数
degenerate = [] # 用来存储每个hopping的简并度,每个hopping方向对应一个数字
con = 0
for line in file: # 接着上面读取到行的位置继续读
temp = line.strip().split() # 移除字符串头尾指定的字符(默认为空格),并以空格将这些字符串分开
t1 = [int(x) for x in temp] #遍历每个字符串并转换为整数
degenerate.extend(t1) # 数据追加
if len(degenerate) == Hopping_number: # 当获取的hopping对应的简并度的个数和hopping方向的数目相等的时候,就停止读取文件
break
# 接下来读取核心的hr参数,也就是不同带之间hopping的大小以及方向,hr文件中剩下所有的数据都是这些信息,因此可以直接读取到文件末尾
Hr = []
for line in file:
temp = line.strip().split() # 先除去空格,再以空格分立成单独的字符串
# 将所有的字符串再转化成数值进行存储
Hr.append([int(temp[0]),int(temp[1]),int(temp[2]),int(temp[3]),int(temp[4]),float(temp[5]),float(temp[6])])
file.close() # 读取完成之后关闭文件
Hr = np.array(Hr) # 将一个list转化成矩阵, 这里存储的是核心的hooping方向以及大小
# 在通过TB数据进行Fourier变换得到动量空间中的模型时,需要利用的hopping R,这里将这些hopping方向R单独提取出来
Hopping_dir = np.zeros([Hopping_number,3],np.int64)
for i in range(Hopping_number):
Hopping_dir[i] = Hr[Band_number**2 * i ,0:3] # 获取所有的hopping方向
#现在得到了每个轨道hopping方向和对应的大小,那么将其全部存储,方便下一步构建Bloch哈密顿量
con1 = 0 # 用来计数,工具人
ham = np.zeros([Hopping_number, Band_number, Band_number], np.complex128)
for ih in range(Hopping_number):
for i1 in range(Band_number):
for i2 in range(Band_number):
ham[ih,i1,i2] = Hr[con1,5] + 1j*Hr[con1,6] # 对每一个hopping方向,存储每个轨道之间的hopping的大小
con1 = con1 + 1
return ham,Hopping_dir,Band_number,Hopping_number
#-------------------------------------------------------------------
def Hamk(hamhr,Hopping_dir,Hopping_number,Band_number,kx,ky):
# 同过TB数据构建动量空间哈密顿量
H = np.zeros([Band_number,Band_number],np.complex128) # 动量空间哈密顿量
for i0 in range(Hopping_number): # 对所有的R求和进行Fourier变换
H += np.exp(-1j*np.dot(Hopping_dir[i0,0:2],[kx,ky]))*hamhr[i0,:,:] # 每个轨道index对应的前面的位相因子是相同的
return H
#-------------------------------------------------------------------
def Band_HighSymmetry():
nx = 100
vals = []
klist = []
for i0 in range(0,nx):
kx = np.pi*i0/nx
klist.append(kx/np.pi)
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
H = Hamk(ham,Hopping_dir,Hopping_number,Band_number,kx,0)
val,vec = np.linalg.eigh(H)
vals.append(val)
for i0 in range(0,nx):
ky = np.pi*i0/nx
klist.append(1 + ky/np.pi)
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
H = Hamk(ham,Hopping_dir,Hopping_number,Band_number,np.pi,ky)
val,vec = np.linalg.eigh(H)
vals.append(val)
for i0 in range(0,nx):
ki = np.pi*i0/nx
klist.append(2 + ki/np.pi)
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
H = Hamk(ham,Hopping_dir,Hopping_number,Band_number,np.pi - ki,np.pi - ki)
val,vec = np.linalg.eigh(H)
vals.append(val)
return klist,vals
#-------------------------------------------------------------------
re1,re2 = Band_HighSymmetry()
plt.plot(re1,re2)
Double Check
这里提示一下,我再选择BHZ模型的参数的时候,$t_x=t_y=-1,A_x=A_y=1.0$,下面用本身的动量空间中的哈密顿量来计算沿着高对称点的能带
def BHZ(kx,ky):
m0 = 1.5
tx = -1.0
ty = -1.0
ax = 1.0
ay = 1.0
s0 = np.array([[1,0],[0,1]])
sx = np.array([[0,1],[1,0]])
sy = np.array([[0,-1j],[1j,0]])
sz = np.array([[1,0],[0,-1]])
g1 = np.kron(s0,sz)
g2 = np.kron(sz,sx)
g3 = np.kron(s0,sy)
ham = np.zeros([g1.shape[0],g1.shape[0]],np.complex128)
ham = (m0 - tx * np.cos(kx) - ty * np.cos(ky))*g1 + ax * np.sin(kx)*g2 + ay * np.sin(ky)*g3
return ham
#-------------------------------------------------------------------------------------------------
def BHZ_High_path():
nx = 100
vals = []
klist = []
for i0 in range(0,nx):
kx = np.pi*i0/nx
klist.append(kx/np.pi)
H = BHZ(kx,0)
val,vec = np.linalg.eigh(H)
vals.append(val)
for i0 in range(0,nx):
ky = np.pi*i0/nx
klist.append(1 + ky/np.pi)
H = BHZ(np.pi,ky)
val,vec = np.linalg.eigh(H)
vals.append(val)
for i0 in range(0,nx):
ki = np.pi*i0/nx
klist.append(2 + ki/np.pi)
H = BHZ(np.pi - ki,np.pi - ki)
val,vec = np.linalg.eigh(H)
vals.append(val)
return klist,vals
#-------------------------------------------------------------------------
r1,r2 = BHZ_High_path()
plt.plot(r1,r2)

可以看到两者的结果是完全相同的,构造完毕。
宇称计算
对于BHZ模型,可以通过宇称来简单的判断它是否是拓扑的,所以这里就想通过数值的方法来计算高对称点上波函的宇称, 从而来判断拓扑与否。这个模型的基矢选择为
\[\psi=(\rvert s\uparrow\rangle,\rvert s\downarrow\rangle),\rvert p_x+ip_y\uparrow\rangle,\rvert p_x-ip_y\uparrow\rangle)\]对应的动量空间中的形式为
\[H(\mathbf{k})=(m_0-t_x\cos k_x-t_y\cos k_y)\sigma_z+ A_x\sin k_x\sigma_xs_z+A\sin k_y\sigma_y\]它的空间反演操作算符为
\[P=\sigma_z\otimes s_0\]这里的$s$轨道再空间反演下是不变的,而在空间反演下$p_x+ip_y\rightarrow p_x-ip_y$,因此空间反演操作就可以表示为上面的形式。
可以判断的是,在写出这个模型的时候,它的基矢中包含了轨道和自旋的信息,所以这里的$\sigma_i$表示的轨道自由度, 而$s_i$表示的则是自旋自由度,而空间反演并不会改变自旋,所以只会对轨道自由度部分有影响,那么就用这个操作算符,来计算BZ高对称点上的宇称。
import numpy as np
import matplotlib.pyplot as plt
def Hamhr():
# ------------------------------------
file = open('wannier90_hr.dat') # 打开TB模型的数据(通常默认文件名为wannier90_hr.dat)
comment = file.readline()
Band_number = int(file.readline())
Hopping_number = int(file.readline()) # 对于单独的一个字符串可以将其转化为整数
degenerate = [] # 用来存储每个hopping的简并度,每个hopping方向对应一个数字
con = 0
for line in file: # 接着上面读取到行的位置继续读
temp = line.strip().split() # 移除字符串头尾指定的字符(默认为空格),并以空格将这些字符串分开
t1 = [int(x) for x in temp] #遍历每个字符串并转换为整数
degenerate.extend(t1) # 数据追加
if len(degenerate) == Hopping_number: # 当获取的hopping对应的简并度的个数和hopping方向的数目相等的时候,就停止读取文件
break
# 接下来读取核心的hr参数,也就是不同带之间hopping的大小以及方向,hr文件中剩下所有的数据都是这些信息,因此可以直接读取到文件末尾
Hr = []
for line in file:
temp = line.strip().split() # 先除去空格,再以空格分立成单独的字符串
# 将所有的字符串再转化成数值进行存储
Hr.append([int(temp[0]),int(temp[1]),int(temp[2]),int(temp[3]),int(temp[4]),float(temp[5]),float(temp[6])])
file.close() # 读取完成之后关闭文件
Hr = np.array(Hr) # 将一个list转化成矩阵, 这里存储的是核心的hooping方向以及大小
# 在通过TB数据进行Fourier变换得到动量空间中的模型时,需要利用的hopping R,这里将这些hopping方向R单独提取出来
Hopping_dir = np.zeros([Hopping_number,3],np.int64)
for i in range(Hopping_number):
Hopping_dir[i] = Hr[Band_number**2 * i ,0:3] # 获取所有的hopping方向
#现在得到了每个轨道hopping方向和对应的大小,那么将其全部存储,方便下一步构建Bloch哈密顿量
con1 = 0 # 用来计数,工具人
ham = np.zeros([Hopping_number, Band_number, Band_number], np.complex128)
for ih in range(Hopping_number):
for i1 in range(Band_number):
for i2 in range(Band_number):
ham[ih,i1,i2] = Hr[con1,5] + 1j*Hr[con1,6] # 对每一个hopping方向,存储每个轨道之间的hopping的大小
con1 = con1 + 1
return ham,Hopping_dir,Band_number,Hopping_number
#-------------------------------------------------------------------
def Hamk(hamhr,Hopping_dir,Hopping_number,Band_number,kx,ky):
# 同过TB数据构建动量空间哈密顿量
H = np.zeros([Band_number,Band_number],np.complex128) # 动量空间哈密顿量
for i0 in range(Hopping_number): # 对所有的R求和进行Fourier变换
H += np.exp(-1j*np.dot(Hopping_dir[i0,0:2],[kx,ky]))*hamhr[i0,:,:] # 每个轨道index对应的前面的位相因子是相同的
return H
#------------------------------------------------------------------------
def Pauli():
s0 = np.array([[1,0],[0,1]])
sx = np.array([[0,1],[1,0]])
sy = np.array([[0,-1j],[1j,0]])
sz = np.array([[1,0],[0,-1]])
return s0,sx,sy,sz
#--------------------------------------------------------------------------
def inversion_parity(kx,ky):
ham,Hopping_dir,Band_number,Hopping_number = Hamhr()
Hk = Hamk(ham,Hopping_dir,Hopping_number,Band_number,kx,ky)
val,vec = np.linalg.eigh(Hk)
s0,sx,sy,sz = Pauli()
P_operator = np.kron(sz,s0)
re1 = np.zeros((2,2),dtype = complex)
for i0 in range(2):
for i1 in range(2):
re1[i0,i1] = np.dot(np.dot(vec[:,i0].T.conj(),P_operator),vec[:,i1])
return np.trace(re1).real.round()
#-------------------------------------------------------------------------
def main():
p1 = inversion_parity(0,0) # (0,0)
p2 = inversion_parity(0,np.pi) # (0,pi)
p3 = inversion_parity(np.pi,0) # (pi,0)
p4 = inversion_parity(np.pi,np.pi) # (pi,pi)
# 计算四个高对称点的宇称本征值
return p1,p2,p3,p4
#------------------------------------------------------------------------
if __name__=='__main__':
p1,p2,p3,p4 = main()
这里来对计算的结果做一些说明,BHZ模型的每条能带都是两重简并的,因此在这种情况下计算高对称点的pairty的时候,哈密顿量会有两个本征态$\psi_1,\psi_2$, 因此在计算的时候需要同时用这两个简并的本征态同时来计算对应的pairty
\[\langle\psi_i\rvert P\rvert\psi_j\rangle\]这时候得到的结果会是一个矩阵,对这个矩阵求trace就可以得到对应的parity。而对于BHZ模型,此时在高对称点上它的宇称则是$\pm 2$,但是着并不影响结果分析,此时的参数对应的正是一个拓扑绝缘体, 因为四个高对称点上的宇称,其中三个是相同的,有一个是相反的,这个宇称相反的位置对应的就是发生能带反转的位置。
代码下载
整个计算过程相应的代码可以点击这里下载。
参考
-
- Berry Phases in Electronic Structure Theory Electric Polarization, Orbital Magnetization and Topological Insulators
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |