这里来整理一下在考虑了次次近邻hopping之后,如何利用迭代格林函数的方法来求解得到系统对应的边界态,这里所有的例子都是以动量空间的哈密顿量为基础,将其 离散化到格点上之后进行计算的。
模型
这里仍然以最简单的Chern绝缘体模型为例子来进行学习
\[H(\mathbf{k})=(m_0-t_x\cos k_x-\cos k_y)\sigma_z+A_x\sin 2k_x\sigma_x+\sin 2k_y\sigma_y\label{s1}\]这里唯一不同的就是此时该模型的Chern数可以是$\pm 1,\pm 3$,而且这里包含着次次近邻之间的hopping。在之前的Blog快速格林函数方法计算Chern绝缘体边界态 中计算的知识包含最近邻的,其实当包含次次近邻hopping的时候,计算思路是完全一致的。
这里只需要将本来的周期性结构扩大,使得在这个更大的原胞中,本来的次近邻hopping变成原胞内的hopping,而在这个更大的原胞的表示下,次次近邻的hopping反而 就变成了最近邻hopping,当将这个问题搞明白之后,那么就只需要构建这个更大的原胞即可。
以Chern绝缘体为例,本来在只有最近邻hopping的情况下,每个原胞有两个轨道,也就是(\ref{s1})中$\sigma$这个Pauli矩阵所代表的自由度,因此快速格林函数方法计算Chern绝缘体边界态 中就给出了如何在这种情况下构建出迭代格林函数所需要的$H00,H01$。但是现在情况只是变成了包含次次近邻hopping的一个模型,那么自然而然就需要将原胞扩大为原来的 两倍,因为只有这样,才可以在这个扩大的原胞下面,将次近邻表示为原胞内的hopping,而次次近邻就会变成较大原胞表示下的次近邻hopping。也就是说此时的每个原胞内 是包含了4个轨道的,分别是原来格点1的两个轨道,格点2的两个轨道
\[\Psi=\{c_{1,a},c_{1,b},c_{2,a},c_{2,b}\}\]那么剩下的问题就是如何构建onsite的$H00$以及现在这个大的原胞下面的hopping的矩阵表示$H01$,而这部分内容的完全就回到的快速格林函数方法计算Chern绝缘体边界态 中的内容。
这里可以拓展一下,无论之后遇到什么样的形式,这里需要做的就是将最远的hooping,利用一个大的原胞将其表示为最近邻hopping,只要做到了这一步,那么剩下的问题就是如何利用迭代格林函数 来计算体态和边界态的性质。
代码
这里是完整的代码,可以先用julia计算得到数据,因为迭代格林函数要想作图精确就需要很大的数据量,所以之后结合Fortran将数据规范化,在结合gnuplot绘图,这里
正是因为数据体量较大,所以借用软件画图可能会很费劲,所以就直接在服务器上进行绘图了。
主程序
using LinearAlgebra,DelimitedFiles
# ========================================================
function Pauli()
hn::Int64 = 2
g1 = zeros(ComplexF64,hn,hn)
g2 = zeros(ComplexF64,hn,hn)
g3 = zeros(ComplexF64,hn,hn)
#------------------------
g1[1,2] = 1
g1[2,1] = 1
g2[1,2] = -im
g2[2,1] = im
g3[1,1] = 1
g3[2,2] = -1
return g1,g2,g3
end
# ========================================================
function openx1(ky::Float64)
# 手动填写最近邻和和次近邻hopping
hn::Int64 = 4
H00 = zeros(ComplexF64,hn,hn)
H01 = zeros(ComplexF64,hn,hn)
#--------------------
m0::Float64 = .5 # C = 3
tx::Float64 = 1.0
ty::Float64 = 1.0
ax1::Float64 = .0
ay1::Float64 = .0
ax2::Float64 = 1.0
ay2::Float64 = 1.0
#--------------------
H00[1,1] = m0 - ty*cos(ky)
H00[2,2] = -m0 + ty*cos(ky)
H00[3,3] = m0 - ty*cos(ky)
H00[4,4] = -m0 + ty*cos(ky)
H00[1,2] = -im*ay1*sin(ky) - im*ay2*sin(2*ky)
H00[2,1] = im*ay1*sin(ky) + im*ay2*sin(2*ky)
H00[3,4] = -im*ay1*sin(ky) - im*ay2*sin(2*ky)
H00[4,3] = im*ay1*sin(ky) + im*ay2*sin(2*ky)
H00[1,3] = -tx/2.0
H00[2,4] = tx/2.0
H00[3,1] = -tx/2.0
H00[4,2] = tx/2.0
H00[1,4] = ax1/(2.0*im)
H00[2,3] = ax1/(2.0*im)
H00[3,2] = -ax1/(2.0*im)
H00[4,1] = -ax1/(2.0*im)
# 次近邻hopping
H01[1,2] = ax2/(2*im)
H01[2,1] = ax2/(2*im)
H01[3,4] = ax2/(2*im)
H01[4,3] = ax2/(2*im)
H01[3,2] = ax1/(2.0*im)
H01[4,1] = ax1/(2.0*im)
H01[3,1] = tx/2.0
H01[4,2] = -tx/2.0
#------
return H00,H01
end
# ==================================================================================
function openx2(ky::Float64)
hn::Int64 = 2 # Dirac 矩阵的维度
on::Int64 = 5 # lattice 数目,这个数目需要包含一个完整的hopping周期
N::Int64 = hn*on
cn::Int64 = hn*2 # 在包含次近邻hopping的时候,元胞的大小是只包含最近邻的2倍
H00 = zeros(ComplexF64,cn,cn)
H01 = zeros(ComplexF64,cn,cn)
Ham = zeros(ComplexF64,N,N)
g1 = zeros(ComplexF64,hn,hn)
g2 = zeros(ComplexF64,hn,hn)
g3 = zeros(ComplexF64,hn,hn)
#--------------------
m0::Float64 = .5
tx::Float64 = 1.0
ty::Float64 = 1.0
ax1::Float64 = 1.0
ay1::Float64 = 1.0
ax2::Float64 = .0
ay2::Float64 = .0
#---------------------------------
g1,g2,g3 = Pauli()
if(N < cn)
println("The lattice number should be large")
end
for ni in 0:on - 1 # 遍历所有格点
if ni == 0
for m in 1:hn
for l in 1:hn
Ham[m,l] = (ay2*sin(ky) + ay1*sin(2*ky))*g2[m,l] + (m0 - ty*cos(ky))*g3[m,l]
Ham[m,l + hn] = -tx/2.0*g3[m,l] + ax2/(2*im)*g1[m,l]
end
end
elseif ni == on - 1
for m in 1:hn
for l in 1:hn
Ham[ni*hn + m,ni*hn + l] = (ay2*sin(ky) + ay1*sin(2*ky))*g2[m,l] + (m0 - ty*cos(ky))*g3[m,l]
Ham[ni*hn + m,ni*hn + l - hn] = -tx/2.0*g3[m,l] - ax2/(2*im)*g1[m,l]
end
end
else
for m in 1:hn
for l in 1:hn
Ham[ni*hn + m,ni*hn + l] = (ay2*sin(ky) + ay1*sin(2*ky))*g2[m,l] + (m0 - ty*cos(ky))*g3[m,l]
Ham[ni*hn + m,ni*hn + l + hn] = -tx/2.0*g3[m,l] + ax2/(2*im)*g1[m,l]
Ham[ni*hn + m,ni*hn + l - hn] = -tx/2.0*g3[m,l] - ax2/(2*im)*g1[m,l]
end
end
end
end
#---------------------------------------------------------------------------------------------
for ni = 0:on - 1
if ni == 0 || ni == 1
for m = 1:hn
for l = 1:hn
Ham[ni*hn + m,ni*hn + l + hn*2] = ax1/(2*im)*g1[m,l]
end
end
elseif ni == on - 1 || ni == on - 2
for m = 1:hn
for l = 1:hn
Ham[ni*hn + m,ni*hn + l - hn*2] = -ax1/(2*im)*g1[m,l]
end
end
else
for m = 1:hn
for l = 1:hn
Ham[ni*hn + m,ni*hn + l + hn*2] = ax1/(2*im)*g1[m,l]
Ham[ni*hn + m,ni*hn + l - hn*2] = -ax1/(2*im)*g1[m,l]
end
end
end
end
#----------------------------------------------------------------------------
# 提取H00与hopping H01
# 这里因为包含次次近邻,相比较于只有最近邻hopping的Chern insulator模型,这个时候需要将元胞扩大
# 令相邻元胞之间等效的也只是包含次近邻hopping,其实相比较于只有最近邻hopping的情况而言,此时元胞的
# 大小是原来的两倍,因为这时候最近邻的相互作用是次次近邻,所以就会使得原来的元胞变成两倍
for i1 in 1:cn
for i2 in 1:cn
H00[i1,i2] = Ham[i1,i2]
H01[i1,i2] = Ham[cn + i1,i2]
end
end
return H00,H01
end
# ====================================================================================
function gf(omg::Float64,ky::Float64,H00::Matrix{ComplexF64},H01::Matrix{ComplexF64})
# 后续可以升级,将H00和H01作为输入参数
hn::Int64 = 4
iter::Int64 = 0
itermax::Int64 = 100
eta::Float64 = 0.01
omegac::ComplexF64 = 0.0
accuarrcy::Float64 = 1E-7
erracc::Float64 = 0.0
epsilon0 = zeros(ComplexF64,hn,hn)
epsilon0s_1 = zeros(ComplexF64,hn,hn)
epsilon0s_2 = zeros(ComplexF64,hn,hn)
epsiloni = zeros(ComplexF64,hn,hn)
epsilonis_1 = zeros(ComplexF64,hn,hn)
epsilonis_2 = zeros(ComplexF64,hn,hn)
alpha0 = zeros(ComplexF64,hn,hn)
alphai = zeros(ComplexF64,hn,hn)
beta0 = zeros(ComplexF64,hn,hn)
betai = zeros(ComplexF64,hn,hn)
unit = zeros(ComplexF64,hn,hn)
GLL = zeros(ComplexF64,hn,hn)
GRR = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
#------------------------------------------
omegac = omg + 1im*eta
epsilon0s_1 = H00
epsilon0s_2 = H00
epsilon0 = H00
alpha0 = H01
beta0 = conj(transpose(H01))
#-------------------------------------
for i in 1:hn
unit[i,i] = 1
end
#--------------------------------------------
for iter in 1:itermax
epsilonis_1 = epsilon0s_1 + alpha0*inv(omegac*unit - epsilon0)*beta0
epsilonis_2 = epsilon0s_2 + beta0*inv(omegac*unit - epsilon0)*alpha0
epsiloni = epsilon0 + alpha0*inv(omegac*unit - epsilon0)*beta0 + beta0*inv(omegac*unit - epsilon0)*alpha0
alphai = alpha0*inv(omegac*unit - epsilon0)*alpha0
betai = beta0*inv(omegac*unit - epsilon0)*beta0
epsilon0s_1 = epsilonis_1
epsilon0s_2 = epsilonis_2
epsilon0 = epsiloni
alpha0 = alphai
beta0 = betai
erracc = abs(sum(alphai))
if erracc < accuarrcy
break
end
end
# GLL = inv(omegac*unit - epsilon0s)
# GBulk = inv(omegac*unit - epsilon0)
GLL = epsilon0s_1
GRR = epsilon0s_2
GBulk = epsilon0
return GLL,GRR,GBulk
end
# ==========================================================
function main()
hn::Int64 = 4
dk::Float64 = 0.01
domg::Float64 = 0.01
ky::Float64 = 0.0
omg::Float64 = 0.0
GLL = zeros(ComplexF64,hn,hn)
GRR = zeros(ComplexF64,hn,hn)
GBulk = zeros(ComplexF64,hn,hn)
f1 = open("test-1.dat","w")
for ky in -pi:dk:pi
h00,h01 = openx1(ky)
# h00,h01 = openx2(ky)
for omg in -3:domg:3
GLL,GRR,GBulk = gf(omg,ky,h00,h01)
re1 = log(-imag(sum(GLL))/pi)
re2 = log(-imag(sum(GRR))/pi) # 取log可能会遇到是负数的情况,这里使用log本来也是为了让结果在数值上好看
re3 = log(-imag(sum(GBulk))/pi)
# re1 = -imag(sum(GLL))/pi
# re2 = -imag(sum(GRR))/pi
# re3 = -imag(sum(GBulk))/pi
writedlm(f1,[ky/pi omg re1 re2 re3],"\t")
end
writedlm(f1,"\n")
end
close(f1)
end
# =========================================================
# @time main()
main()
数据格式化
implicit none
integer m1,m2,m3
call main1()
stop
end program
!=======================================================
subroutine main1()
! 读取不明行数的文件
implicit none
integer count,stat
real h1,h2,h3,h4,h5,h22
h1 = 0
h2 = 0
h3 = 0
h22 = 0
open(1,file = "test.dat")
open(2,file = "test-format.dat")
count = 0
do while (.true.)
count = count + 1
h22 = h1
read(1,*,iostat = STAT)h1,h2,h3,h4,h5
if(h22.ne.h1)write(2,*)"" ! 在这里加空行是为了gnuplot绘制密度图
write(2,999)h1,h2,h3,h4,h5 ! 数据格式化
if(stat .ne. 0) exit ! 当这个参数不为零的时候,证明读取到文件结尾
end do
! write(*,*)h1,h2,h3
! write(*,*)count
close(1)
close(2)
999 format(10f11.6)
return
end subroutine main1
绘图
set encoding iso_8859_1
#set terminal postscript enhanced color
#set output 'arc_r.eps'
#set terminal pngcairo truecolor enhanced font ",50" size 1920, 1680
set terminal png truecolor enhanced font ",50" size 1920, 1680
set output 'Chern-1.png'
#set size 2, 1
#set palette defined ( -10 "#194eff", 0 "white", 10 "red" )
set palette defined ( -10 "blue", 0 "white", 10 "red" )
#set palette rgbformulae 33,13,10
set multiplot layout 2,2
unset ztics
unset key
set pm3d
set border lw 6
#set size ratio 1
set view map
#set xtics
#set ytics
#set xlabel "K_1 (1/{\305})"
#set xlabel "X_1"
#set ylabel "K_2 (1/{\305})"
#set ylabel "Y"
#set ylabel offset 1, 0
set colorbox
set xrange [-1:1]
set yrange [-3:3]
set pm3d interpolate 4,4
#splot 'wavenorm.dat' u 1:2:3 w pm3d
#splot 'wavenorm.dat' u 1:2:3 w pm3d
splot 'test-1.dat' u 1:2:3 w pm3d
splot 'test-1.dat' u 1:2:4 w pm3d
splot 'test-1.dat' u 1:2:5 w pm3d
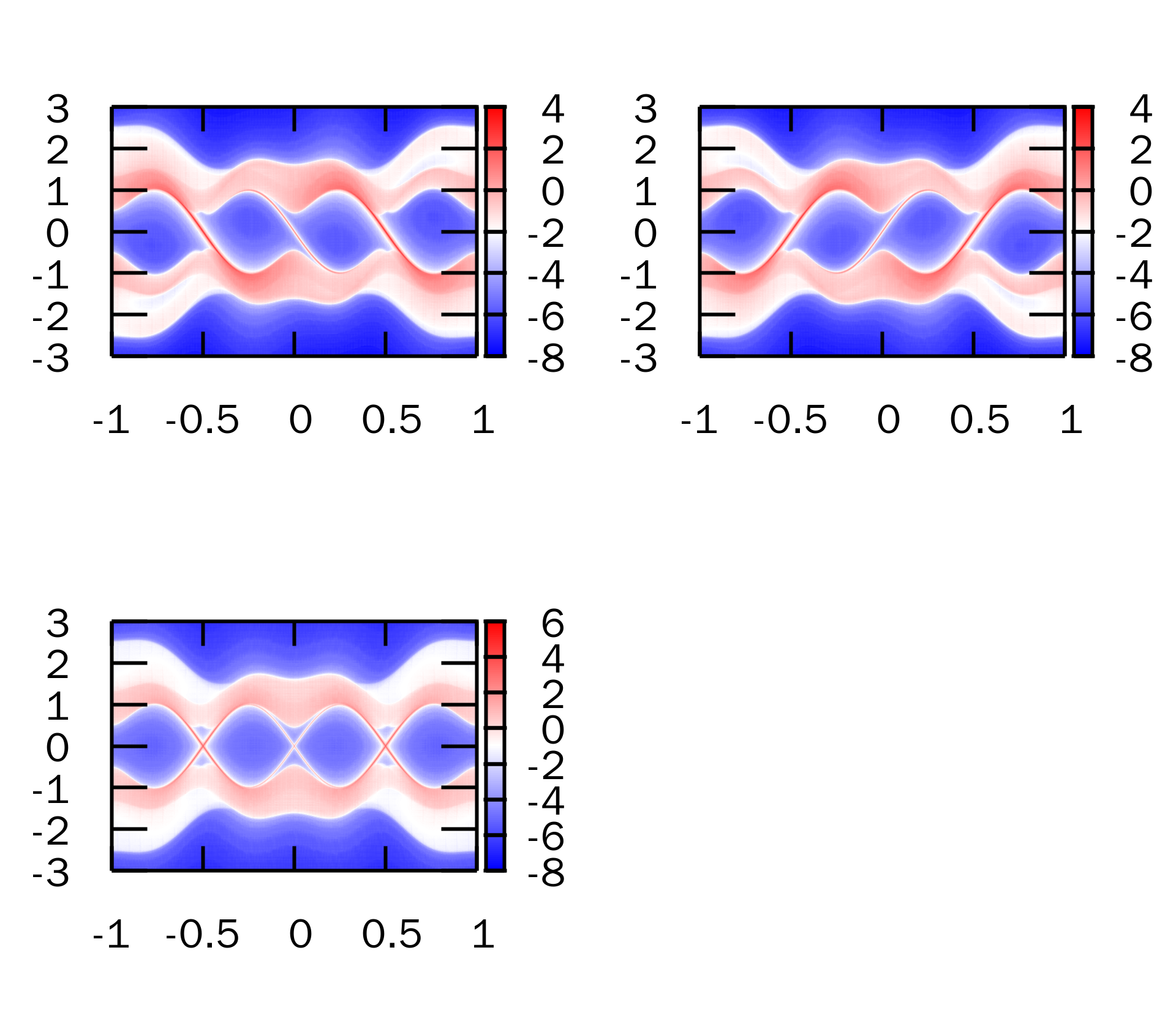
结果
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |