转角石墨烯成为研究热点受到了广泛的关注,最近看到的文献涉及到了相应的内容,虽然不是在研究转角石墨烯的强关联性质,但是还是需要了解如何对转角石墨烯构建有效模型,并通过数值的方式计算能带。这里就整理一下自己在学习twisted bilayer graphene(TBG)时候的笔记,并通过代码来复现Bistritzer-MacDonald模型能带。
单层与双层石墨烯
为了更加清晰明了的理解Bistritzer-MacDonald模型,这里从单层石墨烯出发,逐步理解如何构建紧束缚模型。
单层石墨烯
单层石墨烯的结构如下图所示,其最小原胞如灰色阴影区域所示,其中包含两个不等价的碳原子,这里将其标记为A,B。
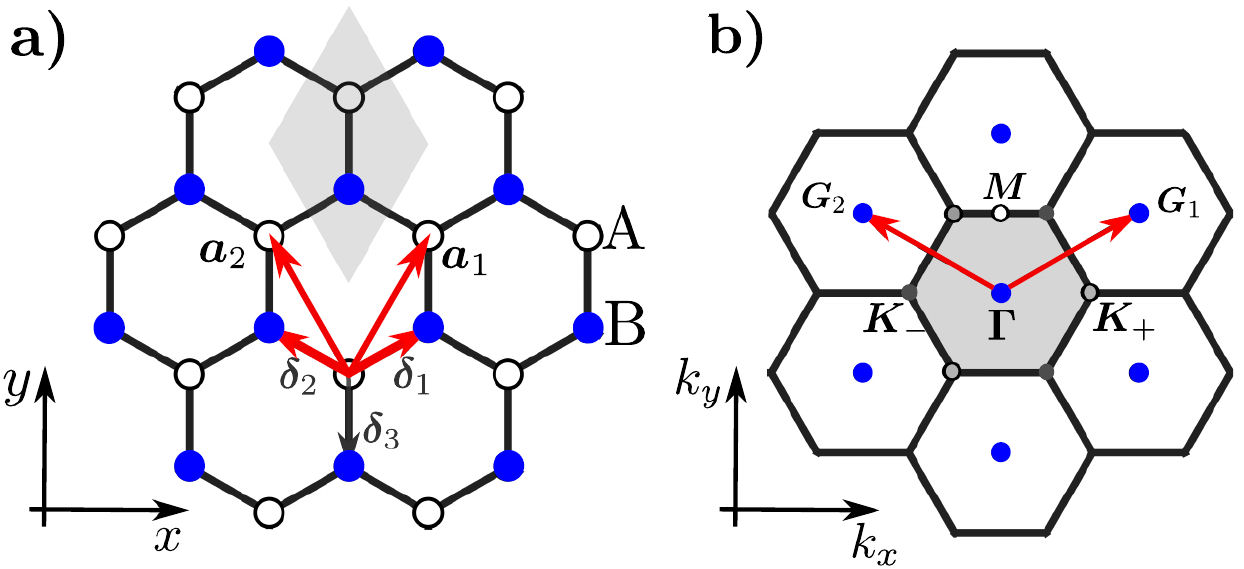
石墨烯的原胞在实空间构成了六角Bravais ${\mathbf{R}}$,这些点阵可以通过矢量进行表示
\[\begin{equation} \mathbf{R}=n_1\mathbf{a}_1+n_2\mathbf{a}_2,\qquad n_1,n_2\in\mathbb{Z} \end{equation}\]这里的$\mathbf{a}_1,\mathbf{a}_2$为原胞基矢
\[\begin{equation} \mathbf{a}_1=a(\frac{1}{2},\frac{\sqrt{3}}{2})\qquad \mathbf{a}_2=a(-\frac{1}{2},\frac{\sqrt{3}}{2}) \end{equation}\]在石墨烯中$a\simeq2.46 A$,两个碳原子之间的距离为$d=1/\sqrt{3}a$,则对应的原胞面积可以通过两个基矢的叉乘得到
\[\begin{equation} A_{\rm U.c}=\rvert \mathbf{a}_1\times\mathbf{a}_2 \rvert=\frac{\sqrt{3}}{2}a^2 \end{equation}\]后面将会关注周期系统,即这里原胞的数量$N=\mathcal{N}_1\mathcal{N}_2(\mathcal{N}_1\rightarrow\infty)$。
紧束缚模型
之前有过一篇博客Graphene紧束缚模型推导整理了石墨烯的模型,这里为了自洽,还是将这部分内容再整理一下。在紧束缚近似中,通常是将电子哈密顿量表示在一些正交的类原子轨道基矢上面(Wannier基矢),利用二次量子化的语言,通常紧束缚模型可以表示为
\[\begin{equation} H=\sum_{\mathbf{R},\mathbf{\delta},\alpha,\beta}c^\dagger_\alpha(\mathbf{R})h^{\alpha\beta}_{\mathbf{\delta}}c_\beta(\mathbf{R}+\mathbf{\delta}) \end{equation}\]这里$c^\dagger_\alpha(\mathbf{R})$表示$\alpha$类型Wannier态的产生算符,它的中心位置为$\mathbf{R}+\mathbf{\tau}\alpha$,这里的$\mathbf{R}$为原胞位置,$\mathbf{\delta}\alpha$则是原子轨道中心相对于原胞中心的位置。在后面的讨论中先忽略自旋,只考虑无自旋的情况。用$\rvert\mathbf{R},\alpha\rangle$表示$c^\dagger_\alpha(\mathbf{R})$产生的态,将一个轨道写在实空间为$w_\alpha(\mathbf{r}-\mathbf{R}-\mathbf{\tau}\alpha)\mathbf{r}$表示位置,$h^{\alpha\beta}\mathbf{\delta}$表示跃迁交叠积分
\[\begin{equation} h^{\alpha\beta}_\mathbf{\delta}=\langle\mathbf{R},\alpha\rvert H\rvert\mathbf{R}+\mathbf{\delta},\beta\rangle \end{equation}\]这里的$\mathbf{\delta}$要遍历所有相邻的原胞。因为我们要考虑的是周期系统,所以系统具有平移对成性,这也就意味着$h^{α\beta}_\mathbf{\delta}$与原胞位置$\mathbf{R}$没有关系。因为Wannier态在实空间都是很局域的,所以对于较大值的$\mathbf{\delta}$,Wannier波函数之间的交叠就会非常小,因为我们在处理问题的时候只会关心少数的几个hopping,通常已经可以很好的描述系统的性质。
对于石墨烯单轨道的紧束缚模型,因为原胞中存在两个不等价的A,B原子,所以此时有两种$p_z$轨道,分别位于A,B原子上($\alpha=A,B$),根据上面所示的石墨烯结构示意图原胞中原子位置为
\[\begin{equation} \mathbf{\tau}_A=(0,0)\qqaud \mathbf{\tau}_B=(0,d) \end{equation}\]在只考虑最进行hopping近似下,系统中就只有onsite展位能与最近邻hopping
\[\begin{equation} \begin{aligned} &h^{AA}_\mathbf{0}=h^{BB}_\mathbf{0}=\epsilon_{p_z}\ &h^{AB}_{\mathbf{\delta}NN}=h^{BA}_{-\mathbf{\delta}NN}\equiv-t \end{aligned} \end{equation}\]这里的$\mathbf{\delta}_{\rm NN}$是最近邻hopping矢量。对于原胞中的A原子,其最近邻的位置是B原子,所以
\[\begin{equation} \mathbf{\delta}_{\rm NN}=\mathbf{0},-\mathbf{a}_1,-\mathbf{a}_2 \end{equation}\]除了最近邻位置,其它更远的hopping在这里就忽略了。根据第一性计算的结果,这里的hopping强度$t=2.97eV$ 。为了不是一般性,这里可以重新第一能量呢零点,将占位能$\epsilon_{p_z}=0$选择为能量零点,此时单层石墨烯的紧束缚哈密顿量为
\[\begin{equation} H=-t \sum_{\mathbf{R}} c_{A}^{\dagger}(\mathbf{R})(c_{A}(\mathbf{R})+c_{B}(\mathbf{R}-\mathbf{a}_{1})+c_{B}(\mathbf{R}-\mathbf{a}_{2}))+\text { h.c. }\label{q1} \end{equation}\]为了将哈密顿量对角化,这里需要使用Bloch定理:在周期系统中,电子的波函数具有Bloch波的形式 \(\begin{equation} \psi_{\mathbf{k},n}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_{\mathbf{k},n}(\mathbf{r}) \end{equation}\)
这里的$\mathbf{k}$是晶体动量,$n$是能带追奥,$u_{\mathbf{k},n}(\mathbf{r})$是周期函数,其周期与晶体点阵相同
\[\begin{equation} u_{\mathbf{k},n}(\mathbf{r})=u_{\mathbf{k},n}(\mathbf{r}+\mathbf{R})\quad\mathbf{R}=n_1\mathbf{a}_1+n_2\mathbf{a}_2,\qquad n_1,n_2\in\mathbb{Z} \end{equation}\]Bloch定理的一个等价表述为:在周期系统中,电子态满足
\[\begin{equation} \psi_{\mathbf{k},n}(\mathbf{r}+\mathbf{R})=e^{i\mathbf{k}\cdot\mathbf{R}}\psi_{\mathbf{k},n}(\mathbf{r}) \end{equation}\]这个电子态是平移算符的本征态,对应的本征值为$e^{i\mathbf{k}\cdot\mathbf{R}}$。石墨烯波函数满足Bloch定理可以利用局域基矢表示出来
\[\begin{equation} \psi_{\mathbf{k},\alpha}(\mathbf{r})=\frac{1}{\sqrt{N}}\sum_\mathbf{R}e^{i\mathbf{k}\cdot(\mathbf{R}+\mathbf{\tau}_\alpha)}w_\alpha(\mathbf{r}-\mathbf{R}-\mathbf{\tau}_\alpha) \end{equation}\]或者可以利用Dirac符号表示
\[\begin{equation} \rvert\psi_{\mathbf{k},\alpha}\rangle=\frac{1}{\sqrt{N}}\sum_\mathbf{R}e^{i\mathbf{k}\cdot(\mathbf{R}+\mathbf{\tau}_\alpha)}\rvert\mathbf{R},\alpha\rangle\label{q2} \end{equation}\]通常情况下,本征态会是一系列类原子轨道波函数的叠加,所以对于单层石墨烯哈密顿量\eqref{q1},其本征态的一般形式为
\[\begin{equation} \rvert\psi_{\mathbf{k}}\rangle=\sum_\alpha u_\alpha(\mathbf{k})\rvert\psi_{\mathbf{k},\alpha}\rangle\label{q3} \end{equation}\]这里的$\alpha$表示的是不同的轨道,因此本征态就表示为不同轨道波函数的叠加态,$u_\alpha(\mathbf{r})$则表示不同轨道分量的振幅。
这里在构建$\rvert\psi_{\mathbf{k},\alpha}\rangle$的时候有一个人为选择性,可以将方程\eqref{q2}中的$e^{i\mathbf{k}\cdot\mathbf{\tau}\alpha}$这个因子略去,从而将其包含在方程\eqref{q3}的振幅$u\alpha({\mathbf{k}})$中,这两种选择都是可以的,只不过就是在计算体系的性质的时候,一些物理算符的表示在这两种表示下面是不同的,当前的笔记中并不涉及到这些内容,所以可以先不考虑这件事情。
不依赖于时间的单粒子薛定谔方程为
\[\begin{equation} H\rvert\psi\rangle=E\rvert E\rangle \end{equation}\]这里$E$是系统能量,将$\rvert\psi\rangle$选取为方程\eqref{q2}的形式,并利用$\langle\mathbf{R},A\rvert$和$\langle\mathbf{R},B\rvert$左乘到方程两侧可以得到
\[\begin{equation} H(\mathbf{k})\cdot\left[ \begin{array}{cc} u_A(\mathbf{k})\\ u_B(\mathbf{k})\\ \end{array} \right]=E\left[ \begin{array}{cc} u_A(\mathbf{k})\\ u_B(\mathbf{k})\\ \end{array} \right] \end{equation}\]这里的$H(\mathbf{k})$是表示在$(\rvert\psi_{\mathbf{k},A},\rvert\psi_{\mathbf{k},B})$基矢下面的哈密顿量,其具体形式为
\[\begin{equation} H=\left[ \begin{array}{cc} 0&-tf(\mathbf{k})\\ -tf^*(\mathbf{k})&0\\ \end{array} \right]\qquad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}_i}\label{q4} \end{equation}\]由下图可知

它们分别表示最格点A最近邻的三个B个点的位置,从而可以得到哈密顿量$H(\mathbf{k})$的本征值为
\[\begin{equation} E_\pm(\mathbf{k})=\pm t\sqrt{4\cos(\frac{\sqrt{3}}{2}d\cdot k_x)\cos(\frac{3}{2}d\cdot k_y)+2\cos(\sqrt{3}d\cdot k_3)+3} \end{equation}\]其对应的能谱为

低能Dirac哈密顿量
在凝聚态系统中,我们通常只是关心系统低能情况下的性质,此时就可以对前面得到的哈密顿量\eqref{q4}进行化简。通过其动量空间中的能谱可以发现单层石墨烯具有gapless的能带交叉点,而且处在布里渊区(BZ)两个不等价位置$K$和$K’$点,其动量空间坐标位置为
\[\begin{equation} K=\frac{4\pi}{3\sqrt{3}d}(1,0) \end{equation}\]在电中性的单层石墨烯中,每个碳原子贡献一个$p_z$轨道来形成能带,而且原胞中原子贡献轨道的数量就对应了能带的数量,在电中性时,每个原胞中只有一个电子,那么此时体系的两条能带就只有最下面的能带$E_{-}(\mathbf{k})$是被占据的,而$E_{+}(\mathbf{k})$则时空带,此时体系的费米能$E=0$正好落在能带交叉点(K和K’),所以此时单层石墨烯的性质就主要有这些点附近的低能电子态决定。将电子的Bloch动量(晶体动量)表示为$\mathbf{k}=\pm K+\mathbf{q}$,将哈密顿量在$K(K’)$附近做Taylor展开并保留到$\mathbf{q}$的一阶项,此时可以得到低能哈密顿量为
\[\begin{equation} H^{\pm K}(\mathbf{q})=\hbar v_F\left[ \begin{array}{cc} 0&\pm q_x-iq_y\\ \pm q_x+iq_y&0 \end{array} \right]=\hbar v_F\mathbf{q}\cdot(\pm\sigma_x,\sigma_y)\label{q5} \end{equation}\]这里$v_f=\frac{3td}{2\hbar}$为费米速度,$\hbar$时普朗克常数,$\sigma_i$则是作用在A,B子格上的Pauli矩阵。通过哈密顿量\eqref{q5}可以看到,单层石墨烯的低能有效哈密顿量类似于无质量的Dirac哈密顿量,$K,K’$点则被称为Dirac点。
倒空间能带折叠描述
通过实空间点阵
\[\begin{equation*} \mathbf{R}=n_1\mathbf{a}_1+n_2\mathbf{a}_2,\qquad n_1,n_2\in\mathbb{Z} \end{equation*}\]可以定义倒空间的格点${\mathbf{G}}$满足
\[\begin{equation*} e^{i\mathbf{G}\cdot\mathbf{R}}=1 \end{equation*}\]这些倒空间中的格点同样可以类似于实空间格点一样形成规则的点阵,称为倒空间点阵,表示为
\[\begin{equation} \mathbf{G}=m_1\mathbf{b}_1+m_2\mathbf{b}_2,\qquad n_1,n_2\in\mathbb{Z} \end{equation}\]这里$\mathbf{b}_1,\mathbf{b}_1$是倒空间中的基矢,它与实空间基矢满足
\[\begin{equation} \mathbf{a}_i\cdot\mathbf{b}_j=2\pi\delta_{ij} \end{equation}\]对于单层石墨烯,可以得到
\[\begin{equation} \mathbf{b}_1=\frac{4\pi}{3d}(\frac{\sqrt{3}}{2},\frac{1}{2}),\quad\mathbf{b}_2=\frac{4\pi}{3d}(\frac{-\sqrt{3}}{2},\frac{1}{2}) \end{equation}\]倒空间格矢如下图所示
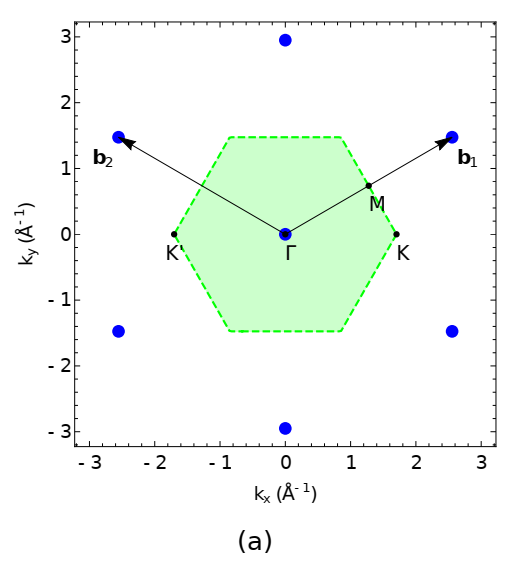
通过Bloch定理可以知道,晶体动量平移整数个倒格矢之后$\mathbf{k}\rightarrow\mathbf{k}+\mathbf{G}$是不变的,这也就意味着我们只需要关注倒空间原胞内的晶体动量就可以了(也就是布里渊区),其它晶体动量处的电子态可以通过平移晶体动量整数个倒格矢得到。
在之前的分析中,我们选择一个最小的原胞进行问题的研究,但其实因为我们研究的是周期系统,并没有那条规定说我们必须选择一个最小的原胞来研究,只要我们选择的这个单元,可以通过平移的方式铺满整个空间就可以。而选择最小的周期单元也只是为了方便进行分析。
现在我们放开限制,在实空间中选择一个更大的原胞,它同样可以通过平移铺满整个实空间。此时动量空间(倒空间)中原胞的面积就会变小,因为实空间与倒空间原胞基矢满足
\[\begin{equation*} \mathbf{a}_i\cdot\mathbf{b}_j=2\pi\delta_{ij} \end{equation*}\]这里可以举个例子,保持原胞的形状不变,还是选择一个菱形的原胞,不过此时其面积会更大包含$2\times3^p(p\in\mathbb{Z})$个碳原子,那么对应的可以得到这种形状原胞构成的点阵的基矢为
\[\begin{equation} \mathbf{a}_1^{(p)}=\sqrt{3}^{p+1}d\left\{ \begin{array}{c} (\frac{1}{2},\frac{\sqrt{3}}{2})\qquad p为偶数\\ (\frac{\sqrt{3}}{2},\frac{1}{2})\qquad p为奇数\\ \end{array} \right. \end{equation}\] \[\begin{equation} \mathbf{a}_2^{(p)}=\sqrt{3}^{p+1}d\left\{ \begin{array}{c} (-\frac{1}{2},\frac{\sqrt{3}}{2})\qquad p为偶数\\ (-\frac{\sqrt{3}}{2},\frac{1}{2})\qquad p为奇数 \end{array} \right. \end{equation}\]当$p=0$的时候就是前面分析对应的最小原胞,$p=1$的结果如下图所示,对应的倒空间中的基矢为
\[\begin{equation} \mathbf{b}_1^{(p)}=\frac{4\pi}{\sqrt{3}^p3d}\left\{ \begin{array}{c} (\frac{\sqrt{3}}{2},\frac{1}{2})\qquad p\text{为偶数}\\ (\frac{1}{2},\frac{\sqrt{3}}{2})\qquad p\text{为奇数} \end{array} \right. \end{equation}\] \[\begin{equation} \mathbf{b}_2^{(p)}=\frac{4\pi}{\sqrt{3}^p3d}\left\{ \begin{array}{c} (-\frac{\sqrt{3}}{2},\frac{1}{2})\qquad p\text{为偶数}\\ (-\frac{1}{2},\frac{\sqrt{3}}{2})\qquad p\text{为奇数} \end{array} \right. \end{equation}\]
从可以看到,随着实空间原胞大小增加,即$\rvert\mathbf{a}^{(p)_i}\rvert$增加,倒空间基矢$\rvert\mathbf{b}^{(p)_i}\rvert$和对应的布里渊区就会减小。同时随着实空间原胞大小的增加,每个原胞中原子的数量会从2变成$2\times 3^p$,那么能量数量也会从2变成$2\times 3^p$。虽然选择实空间的原胞变的不同了,但是不同的选择方式描述的还是同一个系统,那么这些多出来的$2\times 3^{p} - 2$条能带就完全来自于将原本布里渊区中的能带折叠到现在这个更小的布里渊区中。
现在来分析一下在选择了更大的实空间原胞之后,如何构建其动量空间中的哈密顿量。前面虽然是通过紧束缚近似的方法给出的,现在我们选择了一个更大的原胞,那么原则是还是可以通过这个方式来得到动量空间中的哈密顿量,只不过此时因为原胞中包含的原子数量为$2\times 3^p$个,那么Bloch态在构建的时候就需要利用$2\times 3^p$个原子轨道,这样会比较麻烦,这里选择另外一个较为简单点的方式,还是希望可以使用没有发生能带折叠的哈密顿量来构建出有能带折叠的哈密顿量,这种方式给出的物理图像会比较清晰一些。
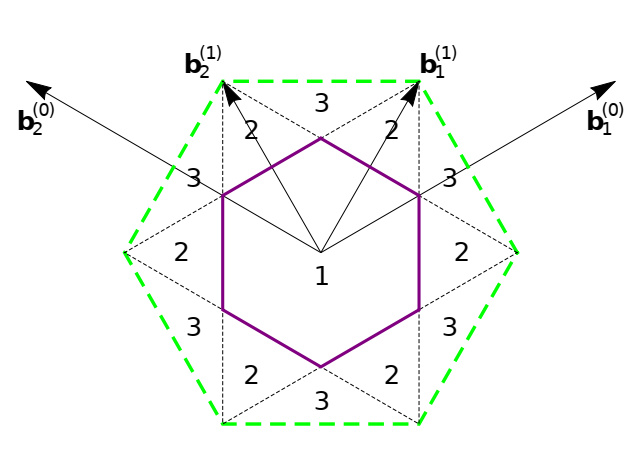
如上图所示,当$p=1$的时候,扩大后的原胞对应的布里渊区是最小原胞($p=0$)的布里渊区的1/3。虽然此时不同原胞选择对应的表示方式变了,但是系统是不变的,那么原始布里渊区中区域2和区域3中的能带信息就会折叠到区域1中,也就是$p=1$对应的布里渊区中。现在假设我们已经有了$p=1$是的哈密顿量,此时原胞中包含6个碳原子,那么我们就一定会有6条能带,如果用拓展布里渊区的方式来表示能带,那么就会有两条能带在第一布里渊区,两条能带在第二布里渊区,还有两条能带在第三布里渊区(这里的拓展布里渊区是对$p=1$而言的),那么这三个布里渊区合起来其实对应的就是$p=0$的第一布里渊区,那么此时就得到了$p=0$时候的能带。这就提供了一个可以将区域1来得到区域2和区域3能带信息的方法,通过观察可以发现,将区域1中的动量$\mathbf{k}$平移$\mathbf{b}_1^{(1)}$就可以等价变成区域2,平移$\mathbf{b}_2^{(2)}$就可以等价变成区域3。前面已经知道,对于区域1中的哈密顿量(其实也就是没有发生能带折叠的哈密顿量)为
\[\begin{equation} H=\left[ \begin{array}{cc} 0&-tf(\mathbf{k})\\ -tf^*(\mathbf{k})&0 \end{array} \right]\qquad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}_i}\label{q4} \end{equation}\]这个哈密顿量可以认为它处在的空间$\rvert\mathbf{k}\rangle$中的(与前面说的$H(\mathbf{k})$是在$\rvert\psi_{\mathbf{k},A}\rangle,\rvert\psi_{\mathbf{k},B}\rangle$上区分一下,其实$\rvert\mathbf{k}\rangle$就是它们的简写),在$p=1$的时候,想要通过$\rvert\mathbf{k}$因为发生了能带折叠,所以此时为了折叠区域的哈密顿量对应的是一个更大的基矢空间
\[\begin{equation} \rvert\mathbf{k}\rangle,\rvert\mathbf{k}+\mathbf{b}_1^{(1)}\rangle,,\rvert\mathbf{k}+\mathbf{b}_2^{(1)}\rangle, \end{equation}\]这里可以符号上会又点让人迷惑,为了和前面说过的$H(\mathbf{k})$是表示在$\rvert\psi_{\mathbf{k},A}\rangle,\rvert\psi_{\mathbf{k},B}\rangle$上一致一些,这里可以将上面的这个基矢完整的表示出来
\[\begin{equation} (\rvert\psi_{\mathbf{k},A}\rangle,\rvert\psi_{\mathbf{k},B}\rangle,\rvert\psi_{\mathbf{k}+\mathbf{b}_1^{(1)},A}\rangle,\rvert\psi_{\mathbf{k}+\mathbf{b}_1^{(1)},B}\rangle,\rvert\psi_{\mathbf{k}+\mathbf{b}_2^{(1)},A}\rangle,\rvert\psi_{\mathbf{k}+\mathbf{b}_2^{(1)},B}\rangle) \end{equation}\]对应的就可以得到在这个基矢下的哈密顿量为
\[\begin{equation} H^{(1)}(\mathbf{k})=\left[ \begin{array}{ccc} H^{(0)}(\mathbf{k})&0&0\\ 0&H^{(0)}(\mathbf{k}+\mathbf{b}_1^{(1)})&0\\ 0&0&H^{(0)}(\mathbf{k}+\mathbf{b}_2^{(1)}) \end{array} \right] \end{equation}\]所以只要知道了最小原胞对应的倒空间哈密顿量$H^{(0)}(\mathbf{k})$以及发生折叠之后的基矢$\mathbf{b}_1^{p-1},\mathbf{b}_2^{p-1}$,将$H^{(0)}(\mathbf{k})$对应的动量进行平移,然后进行直和就可以得到折叠后的哈密顿量。
对于一般的$p>0$可以直接的表示处
\[\begin{equation} H^{(p)}(\mathbf{k})=\left[ \begin{array}{ccc} H^{(p-1)}(\mathbf{k})&0&0\\ 0&H^{(p-1)}(\mathbf{k}+\mathbf{b}_1^{(1)})&0\\ 0&0&H^{(p-1)}(\mathbf{k}+\mathbf{b}_2^{(1)}) \end{array} \right] \end{equation}\]可以看到这个哈密顿量其实是一个递归的形式,想要得到$H^{(p)}(\mathbf{k})$就需要知道$H^{(p-1)}(\mathbf{k})$,而前面分析可以看到$H^{(p-1)}(\mathbf{k})$的构造又需要$H^{(p-2)}(\mathbf{k})$,即
\[\begin{equation} H^{(p-1)}(\mathbf{k})=\left[ \begin{array}{ccc} H^{(p-2)}(\mathbf{k})&0&0\\ 0&H^{(p-2)}(\mathbf{k}+\mathbf{b}_1^{(1)})&0\\ 0&0&H^{(p-2)}(\mathbf{k}+\mathbf{b}_2^{(1)}) \end{array} \right]\quad\cdots,H^{(1)}(\mathbf{k})=\left[ \begin{array}{ccc} H^{(0)}(\mathbf{k})&0&0\\ 0&H^{(0)}(\mathbf{k}+\mathbf{b}_1^{(1)})&0\\ 0&0&H^{(0)}(\mathbf{k}+\mathbf{b}_2^{(1)}) \end{array} \right] \end{equation}\]最终到$H^{(0)}$结束,所以随着实空间中原胞的变大,对应的动量空间布里渊区变小,即$p$增大,那么这个矩阵的维度就会越来越大,所以在实际的计算中,也只是考虑较小的$p$,这些分析在后面推到转角石墨烯的有效哈密顿量的时候会有进一步的体会。
双层石墨烯
双层石墨烯就是将两层单层石墨烯进行堆垛,在实验上测量它们的层间距$d_\perp=3.35A$。这里存在两种堆垛方式
- AA堆垛
- AB堆垛(Bernal stacked)
前面已经说过,单层石墨烯的原胞中有两个不等价的A,B碳原子,所谓的AA堆垛就是下层A型碳原子和上层A型碳原子对齐。而AB堆垛则是下层A型碳原子与上层B型碳原子对齐。这里就只是分析AB堆垛的情况。
紧束缚模型
想要在模型上来模拟AB堆垛的石墨烯,最直接的想法就是想给出单层石墨烯的哈密顿量,再考虑上层与下层格点之间的耦合,而且为了简化,考虑的都是正对格点之间的耦合,那么哈密顿量首先就可以表示为
\[\begin{equation} H=H_1+H_2+H_\perp \end{equation}\]这里$H_i(i=1,2)$为上下单层石墨烯的哈密顿量,$H_\perp$表示不同层石墨烯之间的耦合。利用二次量子化的语言有
\[\begin{equation} \begin{aligned} H_1&=-t\sum_\mathbf{R}c^\dagger_{1,A}(\mathbf{R})[c_{1,B}(\mathbf{R})+c_{1,B}(\mathbf{R}-\mathbf{a}_1)+c_{1,B}(\mathbf{R}-\mathbf{a}_2)]+\text{h.c.}\\ H_2&=-t\sum_\mathbf{R}c^\dagger_{2,A}(\mathbf{R})[c_{2,B}(\mathbf{R})+c_{2,B}(\mathbf{R}-\mathbf{a}_1)+c_{2,B}(\mathbf{R}-\mathbf{a}_2)]+\text{h.c.}\\ \end{aligned} \end{equation}\]这里$c^\dagger_l(\mathbf{R})$为位于原胞$\mathbf{R}$处Wannier态$\rvert l,\mathbf{R},\alpha\rangle$的产生算符。对于层间耦合$H_\perp$,考虑耦合强度是均匀的$t_\perp$,而且只有最近邻层原子之间的耦合
\[\begin{equation} \langle 1\mathbf{R},A\rvert H_\perp\rvert 2,\mathbf{R},B\rangle=t_\perp \end{equation}\]利用二次量子化可以表示为
\[\begin{equation} H_\perp=t_\perp\sum_\mathbf{R}c^\dagger_{1,A}(\mathbf{R})c^\dagger_{2,B}(\mathbf{R})+\text{h.c} \end{equation}\]现在将问题转换到动量空间中进行处理并将哈密顿量表示在Bloch电子态下面
\[\begin{equation} \rvert\psi_{l,\mathbf{k},\alpha}\rangle=\frac{1}{\sqrt{N}}\sum_\mathbf{R}e^{i\mathbf{k}\cdot(\mathbf{R}+\mathbf{\tau}_{l,\alpha})}\rvert l,\mathbf{R},\alpha\rangle \end{equation}\]这里$\mathbf{\tau}_{l,\alpha}$是原胞中四个碳原子相对于原胞中心的位置
\[\begin{equation*} \mathbf{\tau}_{1,A}=\mathbf{\tau}_{2,B}=0\quad \mathbf{\tau}_{1,B}=-\mathbf{\tau}_{2,A}=(0,d) \end{equation*}\]对应的可以将产生算符表示为
\[\begin{equation} c^\dagger_{l,\alpha}(\mathbf{k})=\frac{1}{\sqrt{N}}\sum_\mathbf{R}e^{i\mathbf{k}\cdot(\mathbf{R}+\mathbf{\tau}_{l,\alpha})}c^\dagger_{l,\alpha}(\mathbf{R}) \end{equation}\]其实这个表达式就很熟悉了,就是动量空间和实空间算符之间的Fourier变换,再利用
\[\begin{equation} \sum_\mathbf{R}e^{i\mathbf{R}\cdot(\mathbf{k}-\mathbf{k}')}=N\sum_\mathbf{G}\delta_{\mathbf{k}-\mathbf{k}',\mathbf{G}} \end{equation}\]对于$\mathbf{k},\mathbf{k}’\in$BZ可以得到
\[\begin{equation} \sum_\mathbf{R}e^{i\mathbf{R}\cdot(\mathbf{k}-\mathbf{k}')}=N_{\mathbf{k},\mathbf{k}'} \end{equation}\]那么对应的可以得到
\[\begin{equation} c^\dagger_{l,\alpha}(\mathbf{R})=\frac{1}{\sqrt{N}}\sum_\mathbf{k}e^{-i\mathbf{k}\cdot(\mathbf{R}+\mathbf{\tau}_{l,\alpha})}c^\dagger_{l,\alpha}(\mathbf{k}) \end{equation}\]这里的求和被限制在第一布里渊区(BZ)。因此可以将哈密顿量在二次量子化的下面表示为
\[\begin{equation} H=\sum_\mathbf{k}\Psi^\dagger(\mathbf{k})\cdot H(\mathbf{k})\cdot\Psi(\mathbf{k}) \end{equation}\]这里哈密顿量的基矢为
\[\begin{equation*} \Psi^\dagger(\mathbf{k})=(c^\dagger_{1,A},c^\dagger_{1,B},c^\dagger_{2,A},c^\dagger_{2,B}) \end{equation*}\]哈密顿量的矩阵形式为
\[\begin{equation} H(\mathbf{k})=\left[ \begin{array}{cccc} 0&-tf(\mathbf{k})&0&t_\perp\\ -tf^*(\mathbf{k})&0&0&0\\ 0&0&0&-tf(\mathbf{k})\\ t_\perp&0&-tf^*(\mathbf{k})&0 \end{array} \right]\quad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}} \end{equation}\]通过对角化哈密顿量矩阵$H(\mathbf{k})$就可以得到AB堆垛双层石墨烯的能谱
\[\begin{equation} E_{\pm,\pm}(\mathbf{k})=\pm\sqrt{(\frac{t_\perp}{2t})^2+4\cos(\frac{\sqrt{3}}{2}d\cdot k_x)\cos(\frac{3}{2}d\cdot k_y)+2\cos(\sqrt{3}d\cdot k_x)+3}\pm\frac{t_\perp}{2} \end{equation}\]AB堆垛的能谱如下图所示,可以发现$E_{+,-}(\mathbf{k})$和$E_{-,+}(\mathbf{k})$是交叉的,形成了gapless的点,而且这个点还是处在BZ边界的$K(K’)$点处。
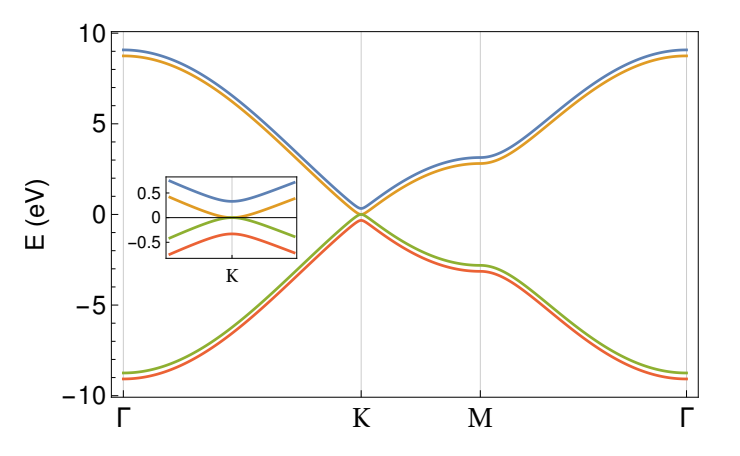
因为这里没有考虑转角,上下两层石墨烯都是正对的,其实要想得到动量空间中的哈密顿量,可以直接从动量空间中来入手,实空间的分析只是为了更加深刻的帮助理解问题。对于两个独立的系统$\mathcal{H}_1,\mathcal{H}_2$,想要研究它们两个耦合在一起的性质,首先第一步就是将它们进行直和
\[\begin{equation} \mathcal{H}=\mathcal{H}_1\oplus\mathcal{H}_2 \end{equation}\]然后再考虑二者之间的耦合$\mathcal{H}_\perp$,这种做法无论是动量空间还是实空间都是如此。而且在直和的时候$\mathcal{H}$对应的基矢就是$\mathcal{H}_i$基矢的直和
\[\begin{equation} \Psi^\dagger=\psi_1\oplus\psi_2 \end{equation}\]对于单层的石墨烯,这里
\[\begin{equation} \Psi=(c_{1,A},c_{1,B},c_{2,A},c_{2,B})\quad \psi_1=(c_{1,A},c_{1,B})\quad \psi_1=(c_{2,A},c_{2,B}) \end{equation}\]所以只需要考虑不同的$c_{l,\alpha}$之间是如何耦合的,就可以表示得到完整的矩阵
\[\begin{equation} \mathcal{H}_\perp=(c^\dagger_{1,A},c^\dagger_{1,B},c^\dagger_{2,A},c^\dagger_{2,B})\left[ \begin{array}{cccc} H_{11}&H_{12}&H_{13}&H_{14}\\ H_{21}&H_{22}&H_{23}&H_{24}\\ H_{31}&H_{32}&H_{33}&H_{34}\\ H_{41}&H_{42}&H_{43}&H_{44}\\ \end{array} \right]\left[ \begin{array}{c} c_{1,A}\\ c_{1,B}\\ c_{2,A}\\ c_{2,B}\\ \end{array} \right] \end{equation}\]对于AB堆垛的石墨烯,这里有
\[\begin{equation*} H_{14}=t_\perp,H_{41}=t_\perp\quad\text{其他}H_{ij}=0 \end{equation*}\]那么如果考虑AA堆垛的双层石墨烯,此时就有
\[\begin{equation*} H_{13}=t_\perp,H_{31}=t_\perp\quad\text{其他}H_{ij}=0 \end{equation*}\]则AA堆垛的双层石墨烯哈密顿量为
\[\begin{equation} H(\mathbf{k})=\left[ \begin{array}{cccc} 0&-tf(\mathbf{k})&t_\perp&0\\ -tf^*(\mathbf{k})&0&0&0\\ t_\perp&0&0&-tf(\mathbf{k})\\ 0&0&-tf^*(\mathbf{k})&0 \end{array} \right]\quad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}} \end{equation}\]转角双层石墨烯
上面分析了很多,就是为了对分析转角双层石墨烯(TBG)进行铺垫,这里就来研究一下怎么样得到TBG的有效模型,不过首先还是要从集合结构出发进行分析。
摩尔条纹(Moir$'e$ pattern)
这从完美堆垛的双层石墨烯出发,考虑AB堆垛,一层固定(记为层1),另外一层进行转动(记为层2),每一层的格点 表示为
\[\begin{equation} \mathbf{R}_l=n_1\mathbf{a}_{l,1}+n_2\mathbf{a}_{l,2}\quad n_1,n_2\in\mathbb{Z} \end{equation}\]这里的$a_{l,i}$表示每一层的基矢,在考虑转角之后,不同层的基矢之间满足
\[\begin{equation} \mathbf{a}_{2,i}=\mathcal{R}_\theta\cdot\mathbf{a}_{1,i} \end{equation}\]其中$\mathcal{R}_\theta$是逆时针的旋转矩阵,2维的旋转矩阵为
\[\begin{equation} \mathcal{R}_\theta=\left[ \begin{array}{cc} \cos(\theta)&-\sin(\theta)\\ \sin(\theta)&\cos(\theta) \end{array} \right] \end{equation}\]每一层石墨烯原胞中的A,B碳原子的位置为
\[\begin{equation} \mathbf{\tau}_{1,A}=(0,0)\quad \mathbf{\tau}_{2,A}=\mathcal{R}_\theta\cdot[(0,-d)+\mathbf{\tau}_0]\\ \mathbf{\tau}_{1,B}=(0,d)\quad \mathbf{\tau}_{2,B}=\mathcal{R}_\theta\cdot[(0,0)+\mathbf{\tau}_0] \end{equation}\]这里的$\mathbf{\tau}0$表示两层之间的相对平移。得到每一层石墨烯实空间点阵${\mathbf{R}_l}$之后,就可以对应的得到倒空间点阵${\mathbf{G}_l}$,倒空间基矢为$\mathbf{b}{l,1},\mathbf{b}_{l,2}$。当两层石墨烯之间存在转角时,每一层倒空间基矢满足
\[\begin{equation} \mathbf{b}_{2,l}=\mathcal{R}_\theta\cdot\mathbf{b}_{1,l} \end{equation}\]当不存在转角的时候,两层石墨烯的基矢是相同的
\[\begin{equation*} \mathbf{b}_{1,1} = \mathbf{b}_{2,1}\quad \mathbf{b}_{1,2} = \mathbf{b}_{2,2} \end{equation*}\]当存在两层存在转角,那么此时会有
\[\begin{equation*} \mathbf{b}_{1,1} \neq \mathbf{b}_{2,1}\quad \mathbf{b}_{1,2} \neq \mathbf{b}_{2,2} \end{equation*}\]那么当不同层的基矢不一致的时候,那么通过基矢进行重复排列时候的周期就会变的不一致,就会类似于经典物理中的两个频率不同的波相遇,产生干涉效应,这也就是为什么会两层石墨烯相互转动可以moir$`e$条纹。更加形象的比喻就是声波的拍频效应,小的周期还会受到一个更大的周期进行调制,如下图所示
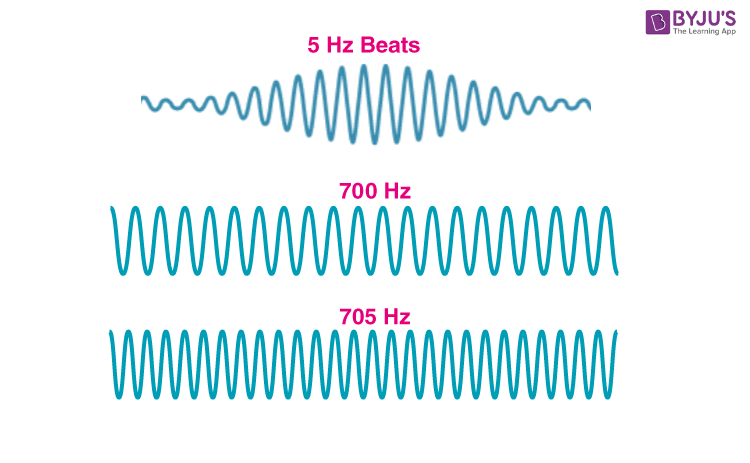
再来仔细理解一下moir$`e$条纹的形成,考虑两个函数$h_1(\mathbf{r}),h_1(\mathbf{r})$具有相同的周期,就像两层石墨烯一样,既然是周期函数,那么就选用最熟悉的三角函数
\[\begin{equation*} h_l(\mathbf{r})=\sum_{k=1}^3\cos(\mathbf{G}_{l,k}\cdot\mathbf{r}) \end{equation*}\]这里记
\[\begin{equation*} \mathbf{G}_{l,1}=\mathbf{b}_{l,1}\quad \mathbf{G}_{l,2}=\mathbf{b}_{l,2}\quad \mathbf{G}_{l,3}=\mathbf{b}_{l,1}-\mathbf{b}_{l,2} \end{equation*}\]两层之间的干涉效应可以通过函数
\[\begin{equation*} h(\mathbf{r})=h_1(\mathbf{r})+h_2(\mathbf{r}) \end{equation*}\]利用和差化积可以得到
\[\begin{equation} h_{m}(\mathbf{r})=\sum_{k=1}^{3} 2 \cos(\frac{\mathbf{G}_{1, k}+\mathbf{G}_{2, k}}{2} \cdot \mathbf{r}) \cos(\frac{\mathbf{G}_{1, k}-\mathbf{G}_{2, k}}{2} \cdot \mathbf{r}) \end{equation}\]所以可以看到这个函数会有一个频率较大的快速震荡$(\mathbf{G}{1,k}+\mathbf{G}{2,k})/2$同时也会受到一个较慢频率$(\mathbf{G}{1,k}-\mathbf{G}{2,k})/2$的包络函数调制,这个包络函数就是对应的是moir$`e$条纹,而频率较大的就是石墨烯自身的周期。包络函数的赋值则会影响摩尔条纹的明暗程度,它会随着$\mathbf{G}{1,k}-\mathbf{G}{2,k}$震荡。因此函数$h_m(\mathbf{r})$将会出现准周期的条纹,与之相对应的倒空间点阵${\mathbf{G}^m}$则是由moir$`e$基矢张开的
\[\begin{equation} \mathbf{b}_1^m=\mathbf{b}_{1,1}-\mathbf{b}_{2,1},\quad \mathbf{b}_2^m=\mathbf{b}_{1,2}-\mathbf{b}_{2,2} \end{equation}\]这里$\mathbf{b}_{l,\alpha}$为单层石墨烯倒空间的基矢,$l$表示不同层指标,$\alpha$则是每一层不同的基矢。
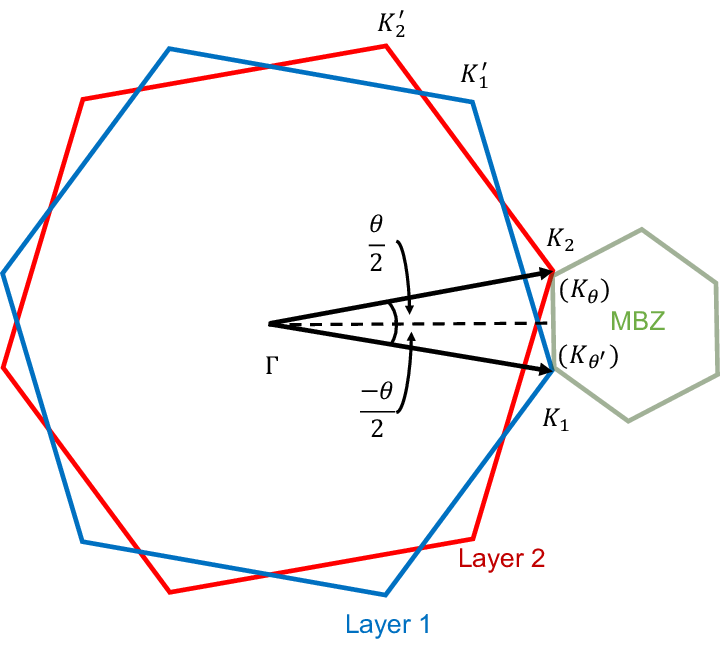
在前面的分析中,我们是将第一层固定,然后第二层转动进行转动,这里选择将第二层转动$\theta/2$,第一层转动$-\theta/2$,此时moir$`e$条纹对应的基矢为
\[\begin{equation} \mathbf{b}_1^m=\sqrt{3}\rvert\Delta K\rvert(\frac{1}{2},-\frac{\sqrt{3}}{2})\quad \mathbf{b}_2^m=\sqrt{3}\rvert\Delta K\rvert(\frac{1}{2},\frac{\sqrt{3}}{2}) \end{equation}\]这里$\rvert\Delta K\rvert=2\rvert\Delta K\rvert\sin(\theta/2)$是两层石墨烯Dirac点相对的偏移距离,这里$\rvert K\rvert=4\pi/(3\sqrt{3}d)$,如下图所示
根据倒空间中的moir$`e$点阵${\mathbf{G}^m}$可以定义实空间的moir$`e$点阵${\mathbf{R}^m}$,实空间的moir$`e$基矢$\mathbf{a}^m_1,\mathbf{a}^m_2$可以通过$\mathbf{a}^m_i\cdot\mathbf{b}^m_j=2\pi\delta_{ij}$,可以得到
\[\begin{equation} \mathbf{a}_1^m=\frac{4\pi}{3\rvert\Delta K\rvert}(\frac{\sqrt{3}}{2},-\frac{1}{2}),\quad \mathbf{a}_2^m=\frac{4\pi}{3\rvert\Delta K\rvert}(\frac{\sqrt{3}}{2},\frac{1}{2}) \end{equation}\]从而可以得到实空间moir$`e$原胞的面积为
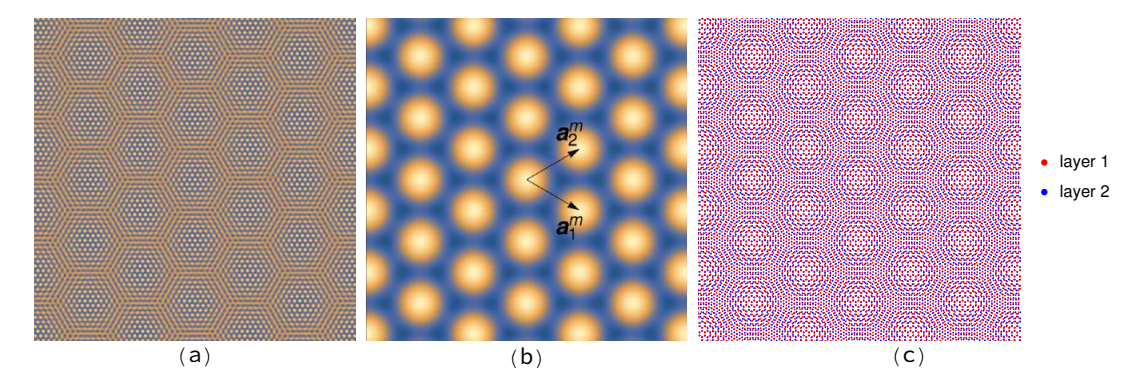
\[\begin{equation} A_{\rm m.u.c}=\rvert\mathbf{a}_1^m\times\mathbf{a}_2^m\rvert=\frac{\sqrt{3}}{2}(\frac{2\pi}{3\rvert\Delta K\rvert})^2=\frac{3\sqrt{3}d^2}{8\sin^2(\theta/2)} \end{equation}\]如下图所示,给出了函数$h_m(\mathbf{r})$的图样以及双层转角石墨烯
模型哈密顿量
旋转单层石墨烯哈密顿量
接下来就来研究一下如何对转角双层石墨烯构建有效模型。这里的出发点与前面讨论双层石墨烯是一样的,紧束缚哈密顿量为
\[\begin{equation} H=H_1+H_1+H_\perp \end{equation}\]这里$H_l$为每一层单独的哈密顿量,$H_\perp=V_{12}+V_{21}$为两层之间的耦合,$V_{12}$表示电子从第二层hopping到第一层,$V_{21}=V^\dagger_{12}$表示相反的过程。在紧束缚近似中通常采取两中心近似,此时就可以将整个哈密顿量根据每一层的Bloch函数表示出来。
我们想要根据每一层的Bloch函数完整的表示出哈密顿量,Bloch函数表示为
\[\begin{equation} \rvert\psi_{l,\mathbf{k},\alpha}\rangle=\frac{1}{\sqrt{N}_l}\sum_{\mathbf{R}_l}e^{i\mathbf{k}\cdot(\mathbf{R}_l+\mathbf{\tau}_{k,\alpha})}\rvert l,\mathbf{R}_l,\alpha\rangle \end{equation}\]这里$l=1,2$代表每一层,$\alpha=A,B$为不等价的子晶格,$\mathbf{N}l$为每一层的原胞数量,$\mathbf{R}_l$是格点位置,$\mathbf{\tau}{l,\alpha}$是原胞中轨道中心的位置,$\rvert l,\mathbf{R}_l,\alpha\rangle$是局域的Wannier态。在这个几基矢下面,考虑单轨道最近邻近似,每一层的哈密顿量为
\[\begin{equation} \begin{aligned} &H_l(\mathbf{k})=\left[ \begin{array}{cc} 0&-tf_l(\mathbf{k})\\ -tf^*_l(\mathbf{k})&0 \end{array} \right]\quad f_l(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot \mathbf{d}_{l,i}}\\ &\mathbf{d}_{l,1}=\frac{1}{3}(\mathbf{a}_{l,1}+\mathbf{a}_{l,2}),\mathbf{d}_{l,2}=\frac{1}{3}(-2\mathbf{a}_{l,1}+\mathbf{a}_{l,2}),\mathbf{d}_{l,3}=\frac{1}{3}(\mathbf{a}_{l,1}-2\mathbf{a}_{l,2}) \end{aligned} \end{equation}\]通常情况下我们只对低能态感兴趣,我们可以在Dirac点$K_l$附近$\mathbf{k}=\pm K_l+\mathbf{q}$将每一层的哈密顿量展开成一个Dirac哈密顿量,这里
\[\begin{equation} K_1=(\frac{4\pi}{3},0),\quad K_2=\mathcal{R}_\theta\cdot K_1 \end{equation}\]展开保留至$\mathbf{q}$的低阶,得到的哈密顿量可以表示为统一的形式
\[\begin{equation} H_l^{\pm K}(\mathbf{q})=\pm\hbar v_F\rvert \mathbf{q}\rvert \left[ \begin{array}{cc} 0&e^{\mp i(\theta_\mathbf{q}-\theta_l)}\\ e^{\pm i(\theta_\mathbf{q}-\theta_l)}&0 \end{array} \right],\quad\theta_1=0,\theta_2=\theta \end{equation}\]这里$\theta_\mathbf{q}$表示动量$\mathbf{q}$和$x$轴的夹角
\[\begin{equation} \mathbf{q}=\rvert \mathbf{q}\rvert (\cos(\theta_\mathbf{q}),\sin(\theta_\mathbf{q})) \end{equation}\]利用Pauli矩阵可以将上面的哈密顿量表示为更加紧凑的形式
\[\begin{equation} H_l^{\pm K}(\mathbf{q})=v_F\hbar\mathbf{q}\cdot(\pm\sigma_x^{\theta_l},\sigma_y^{\theta_l}) \end{equation}\]这里
\[\begin{equation} \sigma_x^\theta=\sigma_x\cos\theta-\sigma_y\sin\theta,\quad\sigma_y^\theta=\sigma_x\sin\theta+\sigma_y\cos\theta \end{equation}\]一般形式层间耦合哈密顿量
在二次量子化描述下,层间耦合哈密顿量写为
\[\begin{equation} V_{12}=\sum_{\mathbf{R}_1,\alpha,\mathbf{R}_2,\beta}c^\dagger_{1,\alpha}t^{\alpha\beta}_{12}(\mathbf{R}_1,\mathbf{R}_2)c_{2,\beta}(\mathbf{R}_2) \end{equation}\]这里
\[\begin{equation} t_{12}^{\alpha\beta}(\mathbf{R}_1,\mathbf{R}_2)=\langle 1,\mathbf{R}_1,\alpha\rvert H_\perp\rvert 2,\mathbf{R}_2,\beta\rangle \end{equation}\]紧束缚基矢下的层间hopping。把算符在Bloch波函数下写出来
\[\begin{equation} c^\dagger_{l,\alpha}(\mathbf{R}_l)=\frac{1}{\sqrt{N}_l}\sum_{\mathbf{k}_l}e^{-i\mathbf{k}\cdot(\mathbf{R}_l+\mathbf{\tau}_{l,\alpha})}c^\dagger_{l,\alpha}(\mathbf{k}_l) \end{equation}\]上面对每一层$\mathbf{k}_l$的求和限制在第一BZ中,从而可以得到
\[\begin{equation} V_{12}=\sum_{\mathbf{k}_{1}, \alpha, \mathbf{k}_{2}, \beta} c_{1, \alpha}^{\dagger}(\mathbf{k}_{1}) T_{12}^{\alpha \beta}(\mathbf{k}_{1}, \mathbf{k}_{2}) c_{2, \beta}^{\dagger}(\mathbf{k}_{2}) \end{equation}\]这里层间耦合矩阵为
\[\begin{equation} T_{12}^{\alpha \beta}(\mathbf{k}_{1}, \mathbf{k}_{2})=\frac{1}{\sqrt{N_{1} N_{2}}} \sum_{\mathbf{R}_{1}, \mathbf{R}_{2}} e^{-i \mathbf{k}_{1} \cdot(\mathbf{R}_{1}+\mathbf{\tau}_{1, \alpha})} t_{12}^{\alpha \beta}(\mathbf{R}_{1}, \mathbf{R}_{2}) e^{i \mathbf{k}_{2} \cdot(\mathbf{R}_{2}+\mathbf{\tau}_{2, \beta})} \end{equation}\]因为这里此时考虑了两层石墨烯,所以在涉及到实空间到动量空间的Fourier变换的时候,两层都要考虑。上面从实空间变化到动量空间中的基矢变化并没有使得问题简化,采用两中心近似可以使得层间耦合简化。假设层间耦合hopping$t_{12}^{\alpha\beta}(\mathbf{R}_1,\mathbf{R}_2)$仅仅是两个轨道中心距离的函数
\[\begin{equation} t_{12}^{\alpha\beta}(\mathbf{R}_1,\mathbf{R}_2)=t_{12}^{\alpha\beta}(\mathbf{R}_1+\mathbf{\tau}_{1,\alpha}-\mathbf{R}_2-\mathbf{\tau}_{2,\beta})\label{q6} \end{equation}\]这里$\mathbf{R}1$是第一层石墨烯的点阵位置,$\mathbf{\tau}{1,\alpha}$则是第一层原子轨道相对于原胞中心的位置,类似的,$\mathbf{R}2,\mathbf{\tau}{2,\beta}$是第二层相对应的量。
通过方程\eqref{q6}可以看到,在两中心近似下,层间耦合在实空间中是一个周期函数,因为每一层石墨烯都是具有周期性的,那么它们点阵位置的差同样会具有周期性,因此可以将层间hopping表示为2D的Fourier变换
\[\begin{equation} t_{12}^{\alpha\beta}(\mathbf{R}_{1}+\mathbf{\tau}_{1,\alpha}-\mathbf{R}_{2}-\mathbf{\tau}_{2,\beta})=\int_{\mathbb{R}^{2}}\frac{d^{2}\mathbf{p}}{(2\pi)^{2}}e^{i\mathbf{p}\cdot(\mathbf{R}_{1}+\mathbf{\tau}_{1,\alpha}-\mathbf{R}_{2}-\mathbf{\tau}_{2,\beta})}t_{12}^{\alpha\beta}(\mathbf{p}).\label{eq:hopping_FT} \end{equation}\]假设$t_{12}^{\alpha\beta}(\mathbf{r})$已知,这里的$\mathbf{r}$表示两个轨道在面内分离的距离,可以通过逆Fourier变换得到动量空间中的$t_{12}^{\alpha\beta}(\mathbf{p})$
\[\begin{equation} t_{12}^{\alpha\beta}(\mathbf{p})=\int_{\mathbb{R}^{2}}d^{2}\mathbf{r}e^{-i\mathbf{p}\cdot\mathbf{r}}t_{12}^{\alpha\beta}(\mathbf{r}).\label{eq:invFT_tp} \end{equation}\]将公式\eqref{eq:hopping_FT}代入到
\[\begin{equation*} T_{12}^{\alpha \beta}(\mathbf{k}_{1}, \mathbf{k}_{2})=\frac{1}{\sqrt{N_{1} N_{2}}} \sum_{\mathbf{R}_{1}, \mathbf{R}_{2}} e^{-i \mathbf{k}_{1} \cdot(\mathbf{R}_{1}+\mathbf{\tau}_{1, \alpha})} t_{12}^{\alpha \beta}(\mathbf{R}_{1}, \mathbf{R}_{2}) e^{i \mathbf{k}_{2} \cdot(\mathbf{R}_{2}+\mathbf{\tau}_{2, \beta})} \end{equation*}\]中可以得到
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{k}_{1},\mathbf{k}_{2})=\frac{1}{\sqrt{N_{1}N_{2}}}\int_{\mathbb{R}^{2}}\frac{d^{2}\mathbf{p}}{(2\pi)^{2}}\sum_{\mathbf{R}_{1}}e^{-i(\mathbf{k}_{1}-\mathbf{p})\cdot(\mathbf{R}_{1}+\mathbf{\tau}_{1,\alpha})}t_{12}^{\alpha\beta}(\mathbf{p})\sum_{\mathbf{R}_{2}}e^{i(\mathbf{k}_{2}-\mathbf{p})\cdot(\mathbf{R}_{2}+\mathbf{\tau}_{2,\beta})}\label{q7} \end{equation}\]使用求和规则
\[\begin{equation*} \sum_{\mathbf{R}_{l}}e^{i\mathbf{k}\cdot\mathbf{R}_{l}}=N_{l}\sum_{\mathbf{G}_{l}}\delta_{\mathbf{k},\mathbf{G}_{l}} \end{equation*}\]可以将方程\eqref{q7}进行化简,得到
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{k}_{1},\mathbf{k}_{2})=\sqrt{N_{1}N_{2}}\int_{\mathbb{R}^{2}}\frac{d^{2}\mathbf{p}}{(2\pi)^{2}}\sum_{\mathbf{G}_{1},\mathbf{G}_{2}}e^{-i\mathbf{G}_{1}\cdot\mathbf{\tau}_{1,\alpha}}t_{12}^{\alpha\beta}(\mathbf{p})e^{i\mathbf{G}_{2}\cdot\mathbf{\tau}_{2,\beta}}\delta_{\mathbf{k}_{1}-\mathbf{p},\mathbf{G}_{1}}\delta_{\mathbf{k}_{2}-\mathbf{p},\mathbf{G}_{2}}. \end{equation}\]接下来利用$\delta$-Kronecker与$\delta$-Dirac函数之间的关系
\[\begin{equation*} \delta_{\mathbf{k},\mathbf{k}^{\prime}}=\delta(\mathbf{k}-\mathbf{k}^{\prime})(2\pi)^{2}/A \end{equation*}\]这里的$A$是体系的总面积,执行对$\mathbf{p}$的积分可以得到
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{k}_{1},\mathbf{k}_{2})=\sqrt{\frac{N_{1}N_{2}}{A^{2}}}\sum_{\mathbf{G}_{1},\mathbf{G}_{2}}e^{-i\mathbf{G}_{1}\cdot\mathbf{\tau}_{1,\alpha}}t_{12}^{\alpha\beta}(\mathbf{k}_{1}+\mathbf{G}_{1})e^{-i\mathbf{G}_{2}\cdot\mathbf{\tau}_{2,\beta}}\delta_{\mathbf{k}_{1}+\mathbf{G}_{1},\mathbf{k}_{2}+\mathbf{G}_{2}},\label{eq:interlayer_hopping_Bloch_0} \end{equation}\]在上面的积分求解中,最主要的结果就是
\[\delta_{\mathbf{k}_{1}-\mathbf{p},\mathbf{G}_{1}}\delta_{\mathbf{k}_{2}-\mathbf{p},\mathbf{G}_{2}}\rightarrow \delta_{\mathbf{k}_{1}+\mathbf{G}_{1},\mathbf{k}_{2}+\mathbf{G}_{2}}\]因为对$\mathbf{G}1,\mathbf{G}_2$的求和是限制在第一BZ中的,因此在方程\eqref{eq:interlayer_hopping_Bloch_0}中将$\mathbf{G}_2\rightarrow-\mathbf{G}_2$是不影响结果的。这里体系的总面积$A=A{u.c.1}N_{1}=A_{u.c.2}N_{2}$,$A_{u.c.l}$是每一层对应的原胞面积($A_{u.c.1}=A_{u.c.2}=A_{u.c.}=\sqrt{3}a^{2}/2$),从而可以将上面的方程表示为
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{k}_{1},\mathbf{k}_{2})=\frac{1}{\sqrt{A_{u.c.1}A_{u.c.2}}}\sum_{\mathbf{G}_{1},\mathbf{G}_{2}}e^{-i\mathbf{G}_{1}\cdot\mathbf{\tau}_{1,\alpha}}t_{12}^{\alpha\beta}(\mathbf{k}_{1}+\mathbf{G}_{1})e^{-i\mathbf{G}_{2}\cdot\mathbf{\tau}_{2,\beta}}\delta_{\mathbf{k}_{1}+\mathbf{G}_{1},\mathbf{k}_{2}+\mathbf{G}_{2}}.\label{eq:interlayer_hopping_Bloch} \end{equation}\]到这里就得到层间耦合在动量空间中的表达式,而且从方程\eqref{eq:interlayer_hopping_Bloch}中可以看到,第一层$l=1$和第二层$l=2$的晶体动量$\mathbf{k}_1,\mathbf{k}_2$需要满足
\[\begin{equation} \mathbf{k}_{1}+\mathbf{G}_{1}=\mathbf{k}_{2}+\mathbf{G}_{2}. \end{equation}\]时才会耦合在一起,被称为一般化的umklapp条件。
$p_z$轨道的层间hopping
在前面,我们只是假设了$t_{12}^{\alpha,\beta}(\mathbf{r})$是已知的,然后得到了层间hopping在动量空间中的具体形式,这里就来明确一下$t_{12}^{\alpha,\beta}(\mathbf{r})$的具体形式。首先因为石墨烯的两个不等间碳原子贡献了相同的$p_z$轨道,所以
\[\begin{equation*} t_{12}^{AA}(\mathbf{r})=t_{12}^{BB}(\mathbf{r})=t_{12}^{AB}(\mathbf{r})=t_{12}^{BA}(\mathbf{r})=t_\perp(\mathbf{r}) \end{equation*}\]在两中心近似下,可以将$t_\perp(\mathbf{r})$根据Slater-Koster参数表示
\[\begin{equation} t_{\perp}(\mathbf{r})=\cos^{2}(\gamma)\ V_{pp\sigma}(\sqrt{d_{\perp}^{2}+\rvert \mathbf{r}\rvert ^{2}})+\sin^{2}(\gamma)\ V_{pp\pi}(\sqrt{d_{\perp}^{2}+\rvert \mathbf{r}\rvert ^{2}}), \end{equation}\]这里$d_{\perp}=3.35A$(这里假设AB堆垛在空间上是均匀的),$\gamma$是两个轨道的连线与$z$轴的夹脚,从而有
\[\begin{equation} \cos^{2}(\gamma)=\frac{d_{\perp}^{2}}{d_{\perp}^{2}+\rvert \mathbf{r}\rvert ^{2}},\quad\sin^{2}(\gamma)=\frac{\rvert \mathbf{r}\rvert ^{2}}{d_{\perp}^{2}+\rvert \mathbf{r}\rvert ^{2}}. \end{equation}\]为了计算$t_\perp(\mathbf{p})$,还是需要明确Slater-Koster参数与两轨道中心分离距离之间的依赖关系。在Numerical studies of confined states in rotated bilayer of graphene这篇文献中已经研究过了$V_{pp\sigma},V_{pp\pi}$的依赖关系
\[\begin{equation} V_{pp\sigma}(r)=t_{\perp}\ \text{exp}\left[q_{\sigma}(1-r/d_{\perp})\right],\quad V_{pp\pi}(r)=-t\ \text{exp}\left[q_{\pi}(1-r/d)\right]. \end{equation}\]它们随着空间距离是指数衰减的。这里要注意
\[\begin{equation*} V_{pp\pi}(d)=-t,\quad V_{pp\sigma}(d_{\perp})=t_{\perp} \end{equation*}\]对应的正是单层石墨烯和AB堆垛的双层石墨烯。为了确定$q_\pi$,作者选择第二近邻hopping的幅值$t’\simeq0.1t$并得到
\[\begin{equation} \frac{V_{pp\pi}(d)}{V_{pp\pi}(\sqrt{3}d)}=\frac{t}{t'}\Leftrightarrow q_{\pi}\simeq3.15. \end{equation}\]剩余的参数$q_\sigma$可以通过假设$\sigma$键和$\pi$键具有相同的空间衰减指数
\[\begin{equation} \frac{q_{\pi}}{d}=\frac{q_{\sigma}}{d_{\perp}}\Leftrightarrow q_{\sigma}\simeq7.42. \end{equation}\]利用这个模型,可以通过计算数值积分得到$t_\perp(\mathbf{p})$
\[\begin{equation} t_{\perp}(\mathbf{p})=2\pi\int_{0}^{\infty}drrJ_{0}(\rvert \mathbf{p}\rvert r)t_{\perp}(r), \end{equation}\]这里$J_0(x)$是第一类Bessel函数,它是由
\[\begin{equation*} t_{12}^{\alpha\beta}(\mathbf{p})=\int_{\mathbb{R}^{2}}d^{2}\mathbf{r}e^{-i\mathbf{p}\cdot\mathbf{r}}t_{12}^{\alpha\beta}(\mathbf{r}) \end{equation*}\]中对角度的积分得到的。通过上面的方程可以看到$t_\perp(\mathbf{p})$仅仅是$\rvert\mathbf{p}\rvert$的函数,当$\rvert\mathbf{p}\rvert$在动量空间中增加时,$t_\perp(\mathbf{p})$会迅速的衰减。直观地说,由于$d_{\perp}>d$增加了2倍以上,因此双中心层间hopping项 $t_{\perp}(\mathbf{r})$依赖与三维空间中的分离距离$\sqrt{\mathbf{r}^{2}+d_{\perp}^{2}}$,对于$\rVert\mathbf{r}\rvert\lesssim d_{\perp}$的情形,$t_\perp(\mathbf{p})$将对$\mathbf{r}$的依赖时比较弱的,因此层间距$d_\perp$对层间hopping占主导作用。因此$t_\perp(\mathbf{r})$在空间中存在一定的展宽,其Fourier变换到动量空间中的$t_\perp(\mathbf{p})$展宽分布较窄,当$\rvert\mathbf{p}\rvert d_\perp>1$的时候就会迅速衰减,如下图所示
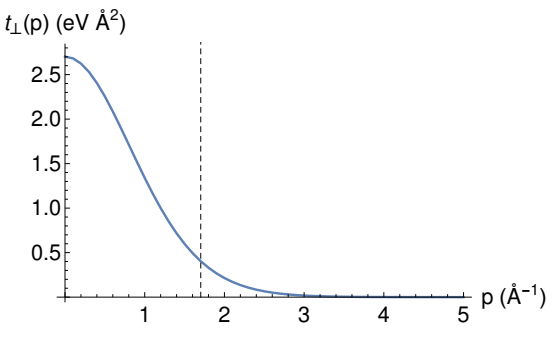
实际上$t_\perp(\mathbf{p})$在$\rvert\mathbf{p}\rvert$较大的时候迅速衰减存在很重要的影响,这也就意味着只有少数的umklapp过程会对层间hopping具有显著的贡献,从而方程 \(T_{12}^{\alpha\beta}(\mathbf{k}_{1},\mathbf{k}_{2})=\frac{1}{\sqrt{A_{u.c.1}A_{u.c.2}}}\sum_{\mathbf{G}_{1},\mathbf{G}_{2}}e^{-i\mathbf{G}_{1}\cdot\mathbf{\tau}_{1,\alpha}}t_{12}^{\alpha\beta}(\mathbf{k}_{1}+\mathbf{G}_{1})e^{-i\mathbf{G}_{2}\cdot\mathbf{\tau}_{2,\beta}}\delta_{\mathbf{k}_{1}+\mathbf{G}_{1},\mathbf{k}_{2}+\mathbf{G}_{2}}\) 中对整个BZ的求和就可以限制在少数的几个离散动量上,这一点我们后面很快就可以利用到。
小转角层间hopping哈密顿量
这里就来研究一下在小转角情况下双层石墨烯的层间耦合时怎样的。对于小转角$\theta$,两层的Dirac点$K_1$和$K_2$就不再重合,在动量空间中它们会相互错开,而且此时忽略$K_l$点与$-K_l$点之间的耦合,因为这两个点在动量空间中相隔距离较远,前面已经讨论过了,$t_\perp(\mathbf{p})$在动量$\rvert\mathbf{p}\rvert$较大的时候会指数衰减,所以就可以忽略它们之间的耦合。

我们这里只关心低能物理,因此可以将所有的量都在Dirac点附近做展开,所以在靠近$K_l$位置处,可以写作
\[\begin{equation} \mathbf{k}_{l}=K_{l}+\mathbf{q}_{l}. \end{equation}\]此时就可以将层间耦合
\[\begin{equation*} T_{12}^{\alpha\beta}(\mathbf{k}_{1},\mathbf{k}_{2})=\frac{1}{\sqrt{A_{u.c.1}A_{u.c.2}}}\sum_{\mathbf{G}_{1},\mathbf{G}_{2}}e^{-i\mathbf{G}_{1}\cdot\mathbf{\tau}_{1,\alpha}}t_{12}^{\alpha\beta}(\mathbf{k}_{1}+\mathbf{G}_{1})e^{-i\mathbf{G}_{2}\cdot\mathbf{\tau}_{2,\beta}}\delta_{\mathbf{k}_{1}+\mathbf{G}_{1},\mathbf{k}_{2}+\mathbf{G}_{2}}.\label{eq:interlayer_hopping_Bloch} \end{equation*}\]表示为
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{q}_{1},\mathbf{q}_{2})=\frac{1}{A_{u.c.}}\sum_{\mathbf{G}_{1},\mathbf{G}_{2}}e^{-i\mathbf{G}_{1}\cdot\mathbf{\tau}_{1,\alpha}}t_{12}^{\alpha\beta}(K_{1}+\mathbf{q}_{1}+\mathbf{G}_{1})e^{-i\mathbf{G}_{2}\cdot\mathbf{\tau}_{2,\beta}}\delta_{K_{1}+\mathbf{q}_{1}+\mathbf{G}_{1},K_{2}+\mathbf{q}_{2}+\mathbf{G}_{2}}. \end{equation}\]对于所有靠近Dirac点的态,满足
\[\begin{equation*} \rvert \mathbf{q}_{1}\rvert ,\rvert \mathbf{q}_{2}\rvert \ll\rvert K\rvert \end{equation*}\]因此可以取近似
\[\begin{equation} t_{\perp}(K_{1}+\mathbf{q}_{1}+\mathbf{G}_{1})\simeq t_{\perp}(K_{1}+\mathbf{G}_{1}) \end{equation}\]正如前面所讨论的,$t_\perp(\mathbf{p})$在$\rvert\mathbf{p}\rvert$较大的时候迅速衰减存在很重要的影响,这也就意味着只有少数的umklapp过程会对层间hopping具有显著的贡献,在这里我们只关注三个最相关的过程,它们对应的层间耦合转移动量都是靠近三个Dirac点。因此可以将$T_{12}^{\alpha\beta}(\mathbf{q}{1},\mathbf{q}{2})$中的求和进行限制
\[\begin{equation} \begin{aligned} \mathbf{G}_{l}&=\mathbf{g}_{l,1},\,\mathbf{g}_{l,2},\,\mathbf{g}_{l,3}\\ \mathbf{g}_{l,1}&=\mathbf{0}, \mathbf{g}_{l,2}=\mathbf{b}_{l,2} \end{aligned} \end{equation}\]最终可以得到层间耦合为
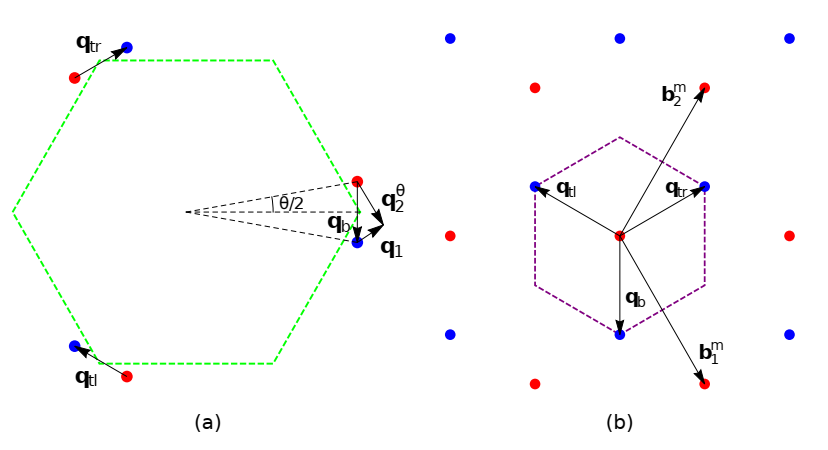
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{q}_{1},\mathbf{q}_{2})=T_{\mathbf{q}_{b}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},-\mathbf{q}_{b}}+T_{\mathbf{q}_{tr}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},-\mathbf{q}_{tr}}+T_{\mathbf{q}_{tl}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},-\mathbf{q}_{tl}},\label{eq:Dirac_interlayer} \end{equation}\]这里对于$n=1(b),2(tr),3(tl)$有$\rvert K_{1}+\mathbf{g}_{1,n}\rvert =\rvert K\rvert =4\pi/(3a)$,在上面的方程中,定义了
\[\begin{equation*} T_{\mathbf{q}_{n}}^{\alpha\beta}=\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{i\mathbf{g}_{1,n}\cdot\mathbf{\tau}_{1,\alpha}}e^{-i\mathbf{g}_{2,n}\cdot\mathbf{\tau}_{2,\beta}} \end{equation*}\]对于石墨烯而言,每个原胞中有A,B两个不等价的碳原子,所以方程\eqref{eq:Dirac_interlayer}中的矩阵分别为
\[\begin{align} T_{\mathbf{q}_{b}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}\left[\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right],\\ T_{\mathbf{q}_{tr}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{-i\mathbf{g}_{1,2}\cdot\mathbf{\tau}_{0}}\left[\begin{array}{cc} e^{i\phi} & 1\\ e^{-i\phi} & e^{i\phi} \end{array}\right],\\ T_{\mathbf{q}_{tl}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{-i\mathbf{g}_{1,3}\cdot\mathbf{\tau}_{0}}\left[\begin{array}{cc} e^{-i\phi} & 1\\ e^{i\phi} & e^{-i\phi} \end{array}\right], \end{align}\]这里有$\phi=2\pi/3$,除此之外还引入了新的矢量
\[\begin{align} \mathbf{q}_{b} & =K_{1}-K_{2},\label{eq:q_b}\\ \mathbf{q}_{tr} & =K_{1}+\mathbf{g}_{1,2}-K_{2}-\mathbf{g}_{2,2},\label{eq:q_tr}\\ \mathbf{q}_{tl} & =K_{1}+\mathbf{g}_{1,3}-K_{2}-\mathbf{g}_{2,3}.\label{eq:q_tl} \end{align}\]考虑第二层转动$\theta/2$,第一层转动$-\theta/2$的时候有
\[\begin{align} \mathbf{q}_{b} & =\rvert \Delta K\rvert (0,-1),\\ \mathbf{q}_{tr} & =\rvert \Delta K\rvert (\frac{\sqrt{3}}{2},\frac{1}{2}),\\ \mathbf{q}_{tl} & =\rvert \Delta K\rvert (-\frac{\sqrt{3}}{2},\frac{1}{2}). \end{align}\]它们在倒空间的如下图所示
上面考虑的是第一层到第二层的hopping,那么第二层倒第一层的hopping就是将方程\eqref{eq:Dirac_interlayer}求厄米共轭即可
\[\begin{equation} T_{21}^{\alpha\beta}(\mathbf{q}_{2},\mathbf{q}_{1})=(T_{\mathbf{q}_{b}}^{\beta\alpha})^{*}\delta_{\mathbf{q}_{2}-\mathbf{q}_{1},\mathbf{q}_{b}}+(T_{\mathbf{q}_{tr}}^{\beta\alpha})^{*}\delta_{\mathbf{q}_{2}-\mathbf{q}_{1},\mathbf{q}_{tr}}+(T_{\mathbf{q}_{tl}}^{\beta\alpha})^{*}\delta_{\mathbf{q}_{2}-\mathbf{q}_{1},\mathbf{q}_{tl}}.\label{eq:Dirac_interlayer_21} \end{equation}\]如果这里取$\theta=0,\mathbf{\tau}_0=0$,那么对应的就是AB堆垛的情况,此时层间耦合为
\[\begin{equation} T_{12}^{\alpha\beta}(\mathbf{q}_{2},\mathbf{q}_{1})=\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}\left\{ \left[\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right]+\left[\begin{array}{cc} e^{i\phi} & 1\\ e^{-i\phi} & e^{i\phi} \end{array}\right]+\left[\begin{array}{cc} e^{-i\phi} & 1\\ e^{i\phi} & e^{-i\phi} \end{array}\right]\right\} =\frac{3t_{\perp}(\rvert K\rvert )}{A_{u.c.}}\left[\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array}\right].\label{eq:Tmatrix_AB_BLG} \end{equation}\]将方程\eqref{eq:Tmatrix_AB_BLG}与前面讨论AB堆垛时候的哈密顿量
\[\begin{equation} H(\mathbf{k})=\left[ \begin{array}{cccc} 0&-tf(\mathbf{k})&0&t_\perp\\ -tf^*(\mathbf{k})&0&0&0\\ 0&0&0&-tf(\mathbf{k})\\ t_\perp&0&-tf^*(\mathbf{k})&0 \end{array} \right]\quad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}} \end{equation}\]进行对比可以得到
\[\begin{equation} t_{\perp}=\frac{3t_{\perp}(\rvert K\rvert )}{A_{u.c.}}. \end{equation}\]通过这个关系可以确定$t_\perp(K)$的值
\[\begin{equation} t_{\perp}(\rvert K\rvert )\simeq0.58 ev\cdot A^2 \end{equation}\]这是一个很好的近似,与恰面的数值结果也是符合的。
上面推导了在$K_l$处的耦合,对于$-K_l$处的耦合,推导方式与$K_l$处是类似的,最终可以得到
\[\begin{equation} \tilde{T}_{12}^{\alpha\beta}(\mathbf{q}_{1},\mathbf{q}_{2})=\tilde{T}_{\mathbf{q}_{b}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},\mathbf{q}_{b}}+\tilde{T}_{\mathbf{q}_{tr}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},\mathbf{q}_{tr}}+\tilde{T}_{\mathbf{q}_{tl}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},\mathbf{q}_{tl}}, \end{equation}\]这里对应的矩阵为
\[\begin{align} \tilde{T}_{\mathbf{q}_{b}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}\left[\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right],\\ \tilde{T}_{\mathbf{q}_{tr}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{i\mathbf{g}_{1,2}\cdot\mathbf{\tau}_{0}}\left[\begin{array}{cc} e^{-i\phi} & 1\\ e^{i\phi} & e^{-i\phi} \end{array}\right],\\ \tilde{T}_{\mathbf{q}_{tl}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{i\mathbf{g}_{1,3}\cdot\mathbf{\tau}_{0}}\left[\begin{array}{cc} e^{i\phi} & 1\\ e^{-i\phi} & e^{i\phi} \end{array}\right]. \end{align}\]电子性质
通过上面的分析,已经得到了转角后的单层石墨烯的哈密顿量以及层间耦合,接下来就分析一下电子的色散关系是如何受到层间耦合影响的。
费米速度重整化
首先来研究对于层间耦合对于一层Dirac点附近电子态的微扰效果。这里考虑第一层,对应的晶体动量为$K_1+\mathbf{q}$,根据层间耦合
\[\begin{equation*} T_{12}^{\alpha\beta}(\mathbf{q}_{1},\mathbf{q}_{2})=T_{\mathbf{q}_{b}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},-\mathbf{q}_{b}}+T_{\mathbf{q}_{tr}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},-\mathbf{q}_{tr}}+T_{\mathbf{q}_{tl}}^{\alpha\beta}\delta_{\mathbf{q}_{1}-\mathbf{q}_{2},-\mathbf{q}_{tl}}, \end{equation*}\]可以看到,这些态仅会与第二层晶体动量为$K_2+\mathbf{q}_2$的态耦合在一起,这里有三个可能的动量$\mathbf{q}_2$
\[\begin{align} \mathbf{q}_{2} & =\mathbf{q}+\mathbf{q}_{b},\quad\mathbf{q}_{2}=\mathbf{q}+\mathbf{q}_{tr},\quad\text{or}\quad\mathbf{q}_{2}=\mathbf{q}+\mathbf{q}_{tl}. \end{align}\]考虑了这些态之后,可以得到下面这个截断的哈密顿量矩阵
\[\begin{equation} H_{4,\text{tBLG}}^{K}(\mathbf{q})=\begin{bmatrix}H_{1}^{K}(\mathbf{q}) & T_{\mathbf{q}_{b}} & T_{\mathbf{q}_{tr}} & T_{\mathbf{q}_{tl}}\\ T_{\mathbf{q}_{b}}^{\dagger} & H_{2}^{K}(\mathbf{q}+\mathbf{q}_{b}) & 0 & 0\\ T_{\mathbf{q}_{tr}}^{\dagger} & 0 & H_{2}^{K}(\mathbf{q}+\mathbf{q}_{tr}) & 0\\ T_{\mathbf{q}_{tl}}^{\dagger} & 0 & 0 & H_{2}^{K}(\mathbf{q}+\mathbf{q}_{tl}) \end{bmatrix},\label{eq:4-wave_truncated_Hamiltonian} \end{equation}\]这个矩阵的基矢为
\[\begin{equation} \rvert 1,K_{1}+\mathbf{q},\alpha\rangle,\rvert 2,K_{2}+\mathbf{q}+\mathbf{q}_{b},\alpha\rangle, \rvert 2,K_{2}+\mathbf{q}+\mathbf{q}_{tr},\alpha\rangle , \rvert 2,K_{2}+\mathbf{q}+\mathbf{q}_{tl},\alpha\rangle \end{equation}\]这里要说明的是,这个矩阵\eqref{eq:4-wave_truncated_Hamiltonian}中的每个子块都是$2\times 2$的矩阵。
当$\rvert \mathbf{q}\rvert\ll\rvert\mathbf{q}n\rvert$且层间耦合$t\perp\ll v_F\hbar\rvert\mathbf{q}_n\rvert$时,可以将\eqref{eq:4-wave_truncated_Hamiltonian}中第二层的态积分掉,从而得到一个关于第一层的有效哈密顿量
\[\begin{equation} H_{1,\text{eff}}^{K}(\mathbf{q})=H_{1}^{K}(\mathbf{q})-\sum_{n=1}^{3}T_{\mathbf{q}_{n}}\cdot\left[H_{2}^{K}(\mathbf{q}+\mathbf{q}_{n})\right]^{-1}\cdot T_{\mathbf{q}_{n}}^{\dagger}. \end{equation}\]通过
\[\begin{equation} H^{\pm K}_l(\mathbf{q})=v_F\hbar\mathbf{q}\cdot(\pm\sigma_x^{\theta_l},\sigma_y^{\theta_l}) \end{equation}\]可以得到
\[\begin{equation} \left[H_{2}^{K}(\mathbf{q})\right]^{-1}=(\mathbf{\sigma}^{\theta}\cdot\mathbf{q})/(v_{F}\hbar\rvert \mathbf{q}\rvert ^{2}) \end{equation}\]展开到$\mathbf{q}$的最低阶得到有效哈密顿量为
\[\begin{equation} H_{1,\text{eff}}^{K}(\mathbf{q})=H_{1}^{K}(\mathbf{q})-\frac{1}{v_{F} \hbar \rvert \Delta K\rvert ^{2}}\sum_{n=1}^{3}\left[T_{\mathbf{q}_{n}}\cdot\mathbf{\sigma}^{\theta}\cdot T_{\mathbf{q}_{n}}^{\dagger}\right]\cdot(\mathbf{q}-\mathbf{q}_{n}+2\mathbf{q}_{n}\frac{\mathbf{q}_{n}\cdot\mathbf{q}}{\mathbf{q}_{n}^{2}}). \end{equation}\]对所有的$\mathbf{q}_n$求和得到
\[\begin{equation} H_{1,\text{eff}}^{ K}(\mathbf{q})=v_{F}\hbar(1-9\alpha^{2})\left[\begin{array}{cc} 0 & q_{x}-iq_{y}\\ q_{x}+iq_{y} & 0 \end{array}\right]-6v_{F}\hbar\rvert \Delta K\rvert \sin(\frac{\theta}{2})\alpha^{2}\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right],\label{eq:vF_renorm_Hamiltonian} \end{equation}\]这里
\[\begin{equation*} \alpha=t_{\perp}(\rvert K\rvert )/(v_{F}\hbar\rvert \Delta K\rvert A_{u.c.}) \end{equation*}\]方程\eqref{eq:vF_renorm_Hamiltonian}中的第二项不过就是将能量在零能进行平移,从第一项中可以发现此时费米速度被重整化了
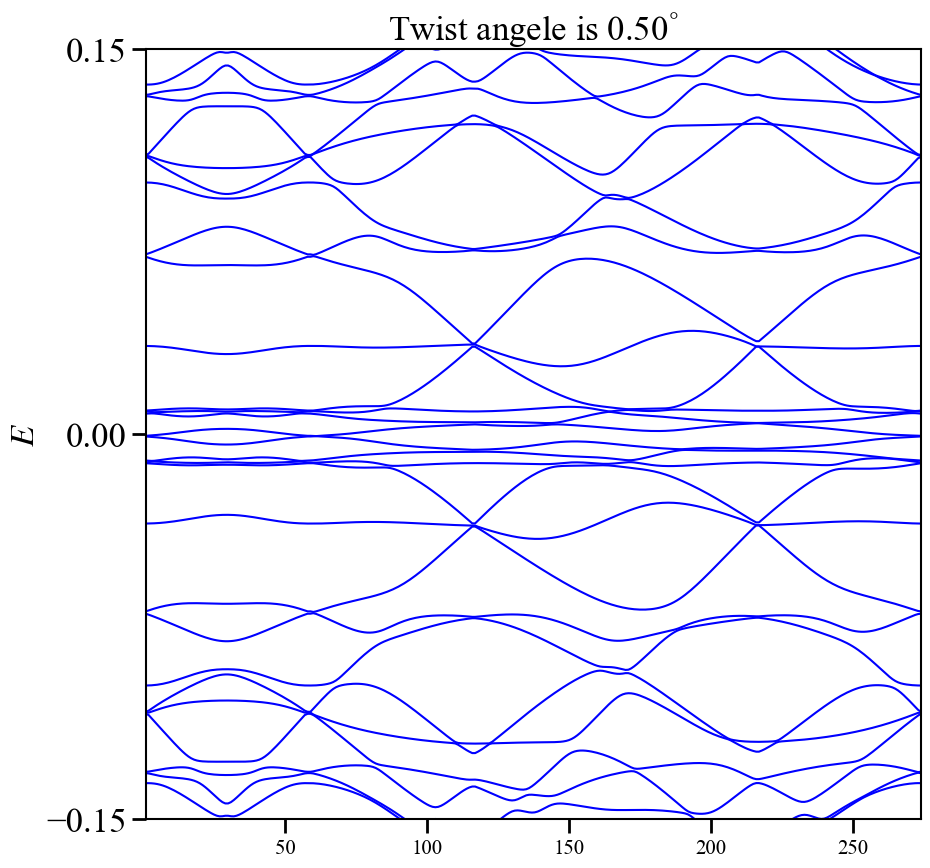
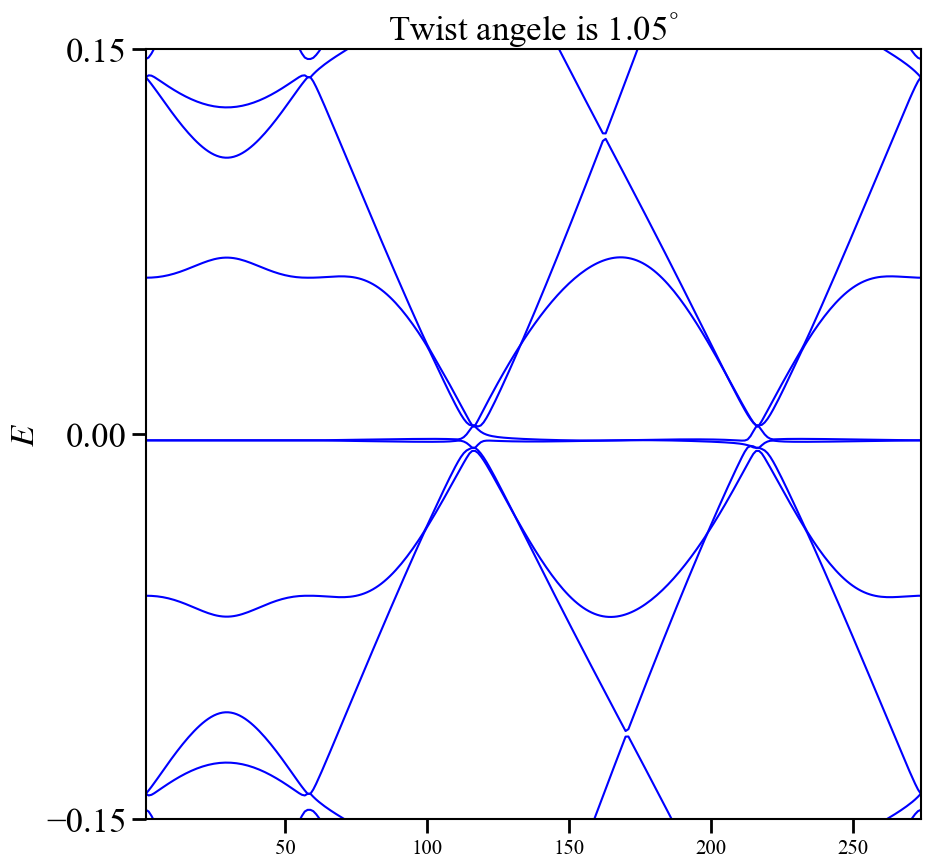
\[\begin{equation} \frac{v_{F}^{*}(\theta)}{v_{F}}=1-(\frac{t_{\perp}(\rvert K\rvert )}{v_{F}\hbar\rvert K\rvert A_{u.c.}})^{2}\frac{1}{4\sin^{2}(\theta/2)}, \end{equation}\]我们可以看到,有效的费米速度时依赖于转角的,对于特殊的转角$\theta$,费米速度会变的非常小,甚至可以变为零。对于很小的转角,其实$t_{\perp}\ll v_{F}\hbar\vert\mathbf{q}_{n}\rvert$这个条件就并不再适用了,上面使用的微扰方法也并不成立,但是在特定的转角下,即魔角附近($\theta\sim1.05^\degree$),费米速度将会变为零,转角双层石墨烯中就会出现平带。
能带结构
为了精确的描述TBG的电子性质,必须超越前面的微扰论,也就是说前面得到的截断的哈密顿量
\[\begin{equation*} H_{4,\text{tBLG}}^{K}(\mathbf{q})=\begin{bmatrix}H_{1}^{K}(\mathbf{q}) & T_{\mathbf{q}_{b}} & T_{\mathbf{q}_{tr}} & T_{\mathbf{q}_{tl}}\\ T_{\mathbf{q}_{b}}^{\dagger} & H_{2}^{K}(\mathbf{q}+\mathbf{q}_{b}) & 0 & 0\\ T_{\mathbf{q}_{tr}}^{\dagger} & 0 & H_{2}^{K}(\mathbf{q}+\mathbf{q}_{tr}) & 0\\ T_{\mathbf{q}_{tl}}^{\dagger} & 0 & 0 & H_{2}^{K}(\mathbf{q}+\mathbf{q}_{tl}) \end{bmatrix}, \end{equation*}\]并不能精确描述TBG,实际上第二层的态$\rvert 2,K_2+\mathbf{q}+\mathbf{q}_n,\alpha\rangle$同样会与第一层的几个态发生耦合,所以上面的这个哈密顿量应该增加它的截断阶数。
在前面讨论最主要的层间耦合贡献的时候,我们已经知道了有三个贡献最大的转移动量$\mathbf{q}b,\mathbf{q}{\rm tr},\mathbf{q}_{\rm tl}$,可以将它们表示为
\[\begin{equation} \mathbf{q}_{b}=\Delta K,\quad\mathbf{q}_{tr}=\Delta K+\mathbf{b}_{2}^{m},\quad\mathbf{q}_{tl}=\Delta K-\mathbf{b}_{1}^{m}, \end{equation}\]这里$\Delta K=2\rvert K\rvert \sin(\theta/2)$时动量空间中两层石墨烯Dirac点之间的距离,通过这个关系可以看到在层间耦合中,转移动量与moir$`e$条纹动量空间的基矢有关系,这使得我们可以将转角石墨烯本征态的结构表示为
\[\begin{equation} \rvert \psi_{\mathbf{q}}^{m}\rangle =\sum_{l,\alpha,m_{1},m_{2}}u_{\alpha}^{(l)}(\mathbf{q},m_{1},m_{2})\rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle ,\label{eq:Bloch-wave_expansion_tBLG} \end{equation}\]这里我们定义
\[\begin{equation} \rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle \equiv\rvert l,\text{K}_{l}+\mathbf{q}+m_{1}\mathbf{b}_{1}^{m}+m_{2}\mathbf{b}_{2}^{m},\alpha\rangle . \end{equation}\]例子
这里考虑一些态(将动量$\mathbf{q}$和子晶格指标先省略,只写出层指标与moir$`e$动量指标)
\[\begin{equation} \rvert 1,(0,0)\rangle ,\,\rvert 2,(0,0)\rangle ,\,\rvert 2,(0,1)\rangle \,\rvert 2,(-1,0)\rangle ,\,\rvert 1,(0,-1)\rangle ,\,\rvert 1,(1,0)\rangle ,\,\rvert 1,(0,1)\rangle ,\,\rvert 1,(1,1)\rangle ,\,\rvert 1,(-1,0)\rangle ,\,\rvert 1,(-1,-1)\rangle \end{equation}\]在这个基矢下面哈密顿量矩阵为
\[\begin{equation} H_{10,\text{TBG}}^{\text{K}}(\mathbf{q})=\left[\begin{array}{cccccccccc} H_{1}^{\text{K}} & T_{\mathbf{q}_{b}} & T_{\mathbf{q}_{tr}} & T_{\mathbf{q}_{tl}} & 0 & 0 & 0 & 0 & 0 & 0\\ T_{\mathbf{q}_{b}}^{\dagger} & H_{2}^{\text{K}} & 0 & 0 & T_{\mathbf{q}_{tr}}^{\dagger} & T_{\mathbf{q}_{tl}}^{\dagger} & 0 & 0 & 0 & 0\\ T_{\mathbf{q}_{tr}}^{\dagger} & 0 & H_{2}^{\text{K}} & 0 & 0 & 0 & T_{\mathbf{q}_{b}}^{\dagger} & T_{\mathbf{q}_{tl}}^{\dagger} & 0 & 0\\ T_{\mathbf{q}_{tl}}^{\dagger} & 0 & 0 & H_{2}^{\text{K}} & 0 & 0 & 0 & 0 & T_{\mathbf{q}_{b}}^{\dagger} & T_{\mathbf{q}_{tr}}^{\dagger}\\ 0 & T_{\mathbf{q}_{tr}} & 0 & 0 & H_{1}^{\text{K}} & 0 & 0 & 0 & 0 & 0\\ 0 & T_{\mathbf{q}_{tl}} & 0 & 0 & 0 & H_{1}^{\text{K}} & 0 & 0 & 0 & 0\\ 0 & 0 & T_{\mathbf{q}_{b}} & 0 & 0 & 0 & H_{1}^{\text{K}} & 0 & 0 & 0\\ 0 & 0 & T_{\mathbf{q}_{tl}} & 0 & 0 & 0 & 0 & H_{1}^{\text{K}} & 0 & 0\\ 0 & 0 & 0 & T_{\mathbf{q}_{b}} & 0 & 0 & 0 & 0 & H_{1}^{\text{K}} & 0\\ 0 & 0 & 0 & T_{\mathbf{q}_{tr}} & 0 & 0 & 0 & 0 & 0 & H_{1}^{\text{K}} \end{array}\right],\label{eq:10_wave_expansion} \end{equation}\]这里为了在表示上简化,将$H_{1/2}^K$的动量指标也省略了,实际上$H_1^K$对应的动量为$\mathbf{q}+m_{1}\mathbf{b}{1}^{m}+m{2}\mathbf{b}{2}^{m}$,对于$H_2^K$为$\mathbf{q}+\mathbf{q}{b}+m_{1}\mathbf{b}{1}^{m}+m{2}\mathbf{b}{2}^{m}$。通过对$H{10,\text{TBG}}^{\text{K}}(\mathbf{q})$进行对角化,就可以近似的得到在moir$`e$ BZ中的能带结构,这里是10表示此时我们考虑的moir$`e$格矢,因为此时还存在子晶格自由度,因此$H_{10,\text{TBG}}^{\text{K}}(\mathbf{q})$实际上是一个$20\times20$的矩阵。如果这里考虑的更多的moir$`e$倒格矢,那么对应的矩阵就会更大,对系统的描述也就更加的精确。
分析到这里可以看到,这个矩阵的构建与之前在讨论单层石墨烯中能带折叠时的情形很类似,实际上如果我们不考虑层间耦合(此时矩阵中只有对角线上的子块矩阵存在,其余位置都是零),我们看到这里基本上是在使用能带折叠描述,它在某种程度上显式地捕获moir$`e$周期性(取决于截断顺序)。在实空间中,这对应于取一个具有moir$`e$周期性的放大单元格。
其实这里的描述的构造TBG模型的方法很类似于DFT里面的平面波展开
\[\begin{equation} \psi_{\mathbf{k},n}(\mathbf{r})=\sum_{\mathbf{G}}u_{\mathbf{k},n}\left(\mathbf{G}\right)e^{i\left(\mathbf{k}+\mathbf{G}\right)\cdot\mathbf{r}},\label{eq:plane_wave_expansion} \end{equation}\]对于TBG而言
\[\begin{equation*} \rvert \psi_{\mathbf{q}}^{m}\rangle =\sum_{l,\alpha,m_{1},m_{2}}u_{\alpha}^{(l)}(\mathbf{q},m_{1},m_{2})\rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle \end{equation*}\]是通过参数$(m_1,m_2)$来控制选择的moir$`e$倒格矢的数量,其实也就是控制求和中的$m_1,m_2$。
在DFT的计算中,比如VASP就是利用平面波作为基函数来对本征态进行展开,并且会选取截断能$E\sim\mathbf{k}^2$,实际上截断对应的也就是晶体动量$\mathbf{k}$倒底要选择几倍的倒格矢(也就是说要落在第几BZ中),这一点就会与TBG中选择截断的moir$`e$的数量是相似的。

上图来源于Google到的一个PPT,可以点击这里查阅。
在DFT的平面展开方程\eqref{eq:plane_wave_expansion}中,通过量子力学我们知道,平面构成完备的基空间其对应的维度时无穷大,所以在实际计算的时候总是会选择一个截断来达到数值精度要求。但是对于TBG的展开
\[\begin{equation*} \rvert \psi_{\mathbf{q}}^{m}\rangle =\sum_{l,\alpha,m_{1},m_{2}}u_{\alpha}^{(l)}(\mathbf{q},m_{1},m_{2})\rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle \end{equation*}\]而言,它可以是有限阶也可以是无限阶,与体系的转角有关系。对于一个公度系统(moir$`e$周期可以表示为两个有理数的商),此时两层之间的耦合只包含确定$\mathbf{G}^m$,此时$\rvert \psi_{\mathbf{q}}^{m}\rangle$的展开就是有限阶的,这里的有限阶描述的系统是精确的。如果系统是非共度的,那么此时展开就会是无限阶的。对于TBG系统而言,在非公度时电子的性质其实与平面内两层相对平移矢量$\mathbf{\tau}_0$是无关的,这一点可以通过一个幺正变换来理解
\[\begin{equation} \rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle\rightarrow e^{i\left(m_{1}\mathbf{b}_{1,1}+m_{2}\mathbf{b}_{1,2}\right)\cdot\mathbf{\tau}_{0}}\rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle \end{equation}\]通过这个变换之后会使得哈密顿量不依赖于$\mathbf{\tau}_0$,而量子力学告诉我们对哈密顿量做幺正变换并不会改变系统的性质,所以不失一般性的都会选择$\mathbf{\tau}_0=0$。但是对于共度系统,体系则是依赖于$\mathbf{\tau}_0$的,比如我们前面在讨论AB堆垛和AA堆垛哈密顿量构建时,AA堆垛和AB堆垛可以通过平移$\mathbf{\tau}_0$得到,即通过平移让上层的B型碳原子对应到下层B型碳原子上方,就可以实现$AB\rightarrow AA$堆垛的变换,但是两种不同堆垛的哈密顿量分别为
\[\begin{equation} H^{AB}(\mathbf{k})=\left[ \begin{array}{cccc} 0&-tf(\mathbf{k})&0&t_\perp\\ -tf^*(\mathbf{k})&0&0&0\\ 0&0&0&-tf(\mathbf{k})\\ t_\perp&0&-tf^*(\mathbf{k})&0 \end{array} \right]\quad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}} \end{equation}\] \[\begin{equation} H^{AA}(\mathbf{k})=\left[ \begin{array}{cccc} 0&-tf(\mathbf{k})&t_\perp&0\\ -tf^*(\mathbf{k})&0&0&0\\ t_\perp&0&0&-tf(\mathbf{k})\\ 0&0&-tf^*(\mathbf{k})&0 \end{array} \right]\quad f(\mathbf{k})=\sum_{i=1}^3e^{i\mathbf{k}\cdot\mathbf{d}} \end{equation}\]可以看到这两个哈密顿量很显然时不等价的,无法通过一个幺正变换将它们相互转换。
代码
代码解析
前面我们已将讲清楚了,可以将TBG哈密顿量的本征态表示为
\[\begin{equation*} \rvert \psi_{\mathbf{q}}^{m}\rangle =\sum_{l,\alpha,m_{1},m_{2}}u_{\alpha}^{(l)}(\mathbf{q},m_{1},m_{2})\rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle \end{equation*}\]这里定义了
\[\begin{equation*} \rvert l,\mathbf{q},(m_{1},m_{2}),\alpha\rangle \equiv\rvert l,\text{K}_{l}+\mathbf{q}+m_{1}\mathbf{b}_{1}^{m}+m_{2}\mathbf{b}_{2}^{m},\alpha\rangle . \end{equation*}\]在基矢中选择$m_1,m_2$的值就决定了我们选择截断的大小,比如选择
\[\begin{equation*} m_1,m_2\in 1,2,\cdots N \end{equation*}\]就表示此时截断为N。其中$l$表示的是层指标,$\alpha$表示子晶格自由度,其实这里可以进行拓展,$\alpha$可以表示任何的內禀自由度(如果在graphene中考虑自旋的话)。在后面的基矢表示中我就先忽略$\alpha$指标,那么在给矩阵赋值的时候,每个值其实对应的就是一个矩阵了。
下面选择基矢为
\[\begin{equation} \begin{aligned} \psi(\mathbf{q})=(&\rvert 1,\mathbf{q}+1\cdot\mathbf{b}_1^m+1\cdot\mathbf{b}_2^m\rangle,\rvert 1,\mathbf{q}+2\cdot\mathbf{b}_1^m+1\cdot\mathbf{b}_2^m\rangle,\rvert 1,\mathbf{q}+2\cdot\mathbf{b}_1^m+2\cdot\mathbf{b}_2^m\rangle\\ &\cdots\rvert 1,\mathbf{q}+N\cdot\mathbf{b}_1^m+N\cdot\mathbf{b}_2^m\rangle,\rvert 2,\mathbf{q}+1\cdot\mathbf{b}_1^m+1\cdot\mathbf{b}_2^m\rangle,\rvert 2,\mathbf{q}+2\cdot\mathbf{b}_1^m+1\cdot\mathbf{b}_2^m\rangle,\\& \rvert 2,\mathbf{q}+2\cdot\mathbf{b}_1^m+2\cdot\mathbf{b}_2^m\rangle,\cdot \rvert 1,\mathbf{q}+N\cdot\mathbf{b}_1^m+N\cdot\mathbf{b}_2^m\rangle)\label{ba1} \end{aligned} \end{equation}\]首先就可以根据这个机选选择构建出矩阵对角线上的元素,对角线上的都是单层石墨烯的哈密顿量,通过我们前面的分析可以将代码写为
function HSLG(vf::Float64,qx::Float64,qy::Float64,kk::Int64,jj::Int64,d::Float64,theta::Float64)
b1m = 8 * pi * sin(abs(theta))/(3 * d) * [1/2,-sqrt(3)/2]
b2m = 8 * pi * sin(abs(theta))/(3 * d) * [1/2,sqrt(3)/2]
kx = qx - kk * b1m[1] - jj * b2m[1]
ky = qy - kk * b1m[2] - jj * b2m[2]
h = -vf * sqrt(kx^2 + ky^2) * [0 exp(im * (angle(kx + im * ky) - theta)); exp(-im * (angle(kx + im * ky) - theta)) 0]
return h
end
下面就通过循环在对角线上填充单层石墨烯的哈密顿量。选择截断大小为$N_1$,习惯的选择
\[\begin{equation} m_1.m_2=-N_1,-N_1+1,\cdots,N_1-1,N_1 \end{equation}\]那么可以选择的摩尔倒格矢共有$2N_1+1$个,虽然这里的选择和前面\eqref{ba1}给出的基矢选择的moire倒格矢不一样,但是在写程序的时候还是按照后面的这个方式来进行的,因为习惯上会将BZ分成正负对称的部分。比如对于正方晶格,BZ可以时$[0,2\pi]$,但是通常会在文献中看到选择的是$[-\pi,\pi]$,没关系,反正都是等价的,相互之间差了一个平移而已。
在确定了moire基矢之后,因为这里还存在着子晶格对称性,所以哈密顿量的维度为
\[\begin{equation} N_{\rm dim}=2\times2\times(2N_1 + 1) \end{equation}\]下面就给出程序的示意循环(不是能运行的程序,后面会给出完整的程序)
#------------------------------------------
@everywhere function diag()
tr::Int64 = 3 # truncation
s::Int64 = (2 * tr + 1)
N::Int64 = s^2
H = zeros(ComplexF64,2 * 2 * N,2 * 2 * N) # Hamiltonian
c = 1
Hdiag = zeros(ComplexF64,2 * 2 * N,2 * 2 * N) # diagonal element
for kk in -tr:tr,jj = -tr:tr
temp = zeros(Float64,2 * N,2 * N)
temp[c,c] = 1
Hdiag += kron(temp,HSLG(vf,kx,ky,kk,jj,d,theta/2)) # 1st layer
c += 1
end
for kk = -tr:tr,jj = -tr:tr
temp = zeros(Float64,2 * N,2 * N)
temp[c,c] = 1
Hdiag += kron(temp,HSLG(vf,kx - qb[1],ky - qb[2],kk,jj,d,-theta/2)) # 2nd layer
c += 1
end
end
考虑完了对角线元素,那么接下来就考虑层间耦合带来的非对角元素。前面已经得到层间耦合有
\[\begin{equation*} \mathbf{q}_{b}=\Delta K,\quad\mathbf{q}_{tr}=\Delta K+\mathbf{b}_{2}^{m},\quad\mathbf{q}_{tl}=\Delta K-\mathbf{b}_{1}^{m}, \end{equation*}\]也就是说,如果第一层和第二层的moire倒格矢完全相同($\mathbf{q}_b$),那么对应的散射矩阵就是
\[\begin{equation} \mathbf{q}_b\rightarrow T_{\mathbf{q}_b} \end{equation}\]当第一层与第二层的moire倒格矢相差$\mathbf{b}_2^m$时对应的散射矩阵为
\[\begin{equation} \mathbf{q}_{tr}\rightarrow T_{\mathbf{q}_{tr}} \end{equation}\]当第一层与第二层的moire倒格矢相差$\mathbf{b}_1^m$时对应的散射矩阵为
\[\begin{equation} \mathbf{q}_{tl}\rightarrow T_{\mathbf{q}_{tl}} \end{equation}\]这里
\[\begin{equation*} \begin{aligned} T_{\mathbf{q}_{b}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}\left[\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right],\\ T_{\mathbf{q}_{tr}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{-i\mathbf{g}_{1,2}\cdot\mathbf{\tau}_{0}}\left[\begin{array}{cc} e^{i\phi} & 1\\ e^{-i\phi} & e^{i\phi} \end{array}\right],\\ T_{\mathbf{q}_{tl}} & =\frac{t_{\perp}(\rvert K\rvert )}{A_{u.c.}}e^{-i\mathbf{g}_{1,3}\cdot\mathbf{\tau}_{0}}\left[\begin{array}{cc} e^{-i\phi} & 1\\ e^{i\phi} & e^{-i\phi} \end{array}\right], \end{aligned} \end{equation*}\]这里表示散射矩阵中虽然包含了平移矢量$\mathbf{\tau}_0$,但是在前面的讨论中我们说过了,这个平移矢量在特殊情况下时不会影响能带结构的。
Hoff1 = zeros(ComplexF64,2 * N,2 * N) # off-diagonal element
Hoff2 = zeros(ComplexF64,2 * N,2 * N)
for k2 in -tr:tr,j2 in -tr:tr,k1 in -tr:tr,j1 in -tr:tr
if k1 == k2 && j1 == j2
off1 = zeros(ComplexF64,N,N)
off1[(k1 + tr) * s + j1 + tr + 1,(k2 + tr) * s + j2 + tr + 1] = 1
Hoff1 += kron(off1,Tb)
off2 = zeros(ComplexF64,N,N)
off2[(k2 + tr) * s + j2 + tr + 1,(k1 + tr) * s + j1 + tr + 1] = 1
Hoff2 += kron(off2,Tb')
elseif k1 == k2 && j1 + 1 == j2
off1 = zeros(ComplexF64,N,N)
off1[(k1 + tr) * s + j1 + tr + 1,(k2 + tr) * s + j2 + tr + 1] = 1
Hoff1 += kron(off1,Ttr)
off2 = zeros(ComplexF64,N,N)
off2[(k2 + tr) * s + j2 + tr + 1,(k1 + tr) * s + j1 + tr + 1] = 1
Hoff2 += kron(off2,Ttr')
elseif k1 - 1 == k2 && j1 == j2
off1 = zeros(ComplexF64,N,N)
off1[(k1 + tr) * s + j1 + tr + 1,(k2 + tr) * s + j2 + tr + 1] = 1
Hoff1 += kron(off1,Ttl)
off2 = zeros(ComplexF64,N,N)
off2[(k2 + tr) * s + j2 + tr + 1,(k1 + tr) * s + j1 + tr + 1] = 1
Hoff2 += kron(off2,Ttl')
end
end
Hoff = kron([0 1;0 0],Hoff1) + kron([0 0;1 0],Hoff2)
因为这里考虑的是层间耦合,而且在散射矩阵$T_{\mathbf{q}b},T{\mathbf{q}{tr}},T{\mathbf{q}_{tl}}$是$2\times 2$的矩阵,其实也就是子晶格对称性带来的自由度,所以就需要对构建好的耦合矩阵再直积上一个非对角的矩阵来代表耦合,而且在前面的分析中,耦合有两部分。
\[\begin{equation} V=V_{12}+V_{21} \end{equation}\]从而也就是程序中的
Hoff = kron([0 1;0 0],Hoff1) + kron([0 0;1 0],Hoff2)
完整程序
@everywhere using SharedArrays, LinearAlgebra,Distributed,DelimitedFiles,Printf,Arpack
#-----------------------------------------
@everywhere function HSLG(vf::Float64,qx::Float64,qy::Float64,kk::Int64,jj::Int64,d::Float64,theta::Float64)
b1m = 8 * pi * sin(abs(theta))/(3 * d) * [1/2,-sqrt(3)/2]
b2m = 8 * pi * sin(abs(theta))/(3 * d) * [1/2,sqrt(3)/2]
kx = qx - kk * b1m[1] - jj * b2m[1]
ky = qy - kk * b1m[2] - jj * b2m[2]
h = -vf * sqrt(kx^2 + ky^2) * [0 exp(im * (angle(kx + im * ky) - theta)); exp(-im * (angle(kx + im * ky) - theta)) 0]
return h
end
#-----------------------------------------------------
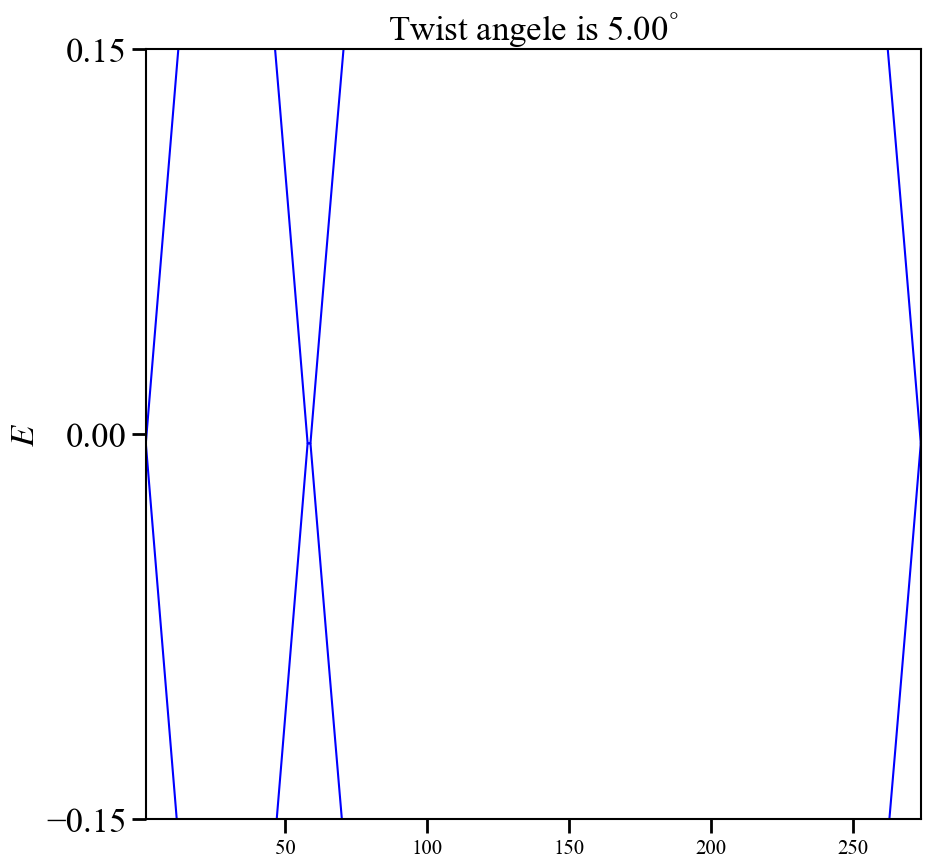
@everywhere function band(ang::Float64)
# ang is twist angle
d::Float64 = 1.42 # nearest c-c bond length
vf::Float64 = 5.944 # Fermi velocity
phi::Float64 = 2 * pi/3
# theta::Float64 = 1.05/180 * pi
theta::Float64 = ang/180 * pi
w1::Float64 = 0.110
tr::Int64 = 3 # truncation
s::Int64 = (2 * tr + 1)
N::Int64 = s^2
Tb = w1 * ones(2,2) # 对角单位矩阵
Ttr = w1 * [exp(-im * phi) 1; exp(im * phi) exp(-im * phi)]
Ttl = w1 * [exp(im * phi) 1; exp(-im * phi) exp(im * phi)]
qb = 8 * pi * sin(theta/2)/(3 * sqrt(3) * d) * [0, -1]
qtr = 8 * pi * sin(theta/2)/(3 * sqrt(3) * d) * [sqrt(3)/2,1/2]
qtl = 8 * pi * sin(theta/2)/(3 * sqrt(3) * d) * [-sqrt(3)/2,1/2]
# geaphene具有A,B子晶格
H = zeros(ComplexF64,2 * 2 * N,2 * 2 * N) # Hamiltonian
N1y = collect(range(-1,0,58)) .* norm(qb)
N1x = 0 * N1y
N2y = collect(range(0,1,58)) .* norm(qb)
N2x = 0 * N2y
N3y = collect(range(1,-1/2,100)) .* norm(qb)
N3x = (-N3y .+ norm(qb))/sqrt(3)
N4y = collect(range(-1/2,-1,58)) .* norm(qb)
N4x = (N4y .+ norm(qb)) * sqrt(3)
Nx = append!(N1x,N2x,N3x,N4x)
Ny = append!(N1y,N2y,N3y,N4y) # k-path : A - B - C - D - A
# band = zeros(length(Nx),4 * N)
band = SharedArray(zeros(Float64,length(Nx),4 * N))
#-----------------------------------------
@sync @distributed for ii in eachindex(Nx)
kx = Nx[ii]
ky = Ny[ii]
c = 1
Hdiag = zeros(ComplexF64,2 * 2 * N,2 * 2 * N) # diagonal element
for kk in -tr:tr,jj = -tr:tr
temp = zeros(Float64,2 * N,2 * N)
temp[c,c] = 1
Hdiag += kron(temp,HSLG(vf,kx,ky,kk,jj,d,theta/2)) # 1st layer, red points
c += 1
end
for kk = -tr:tr,jj = -tr:tr
temp = zeros(Float64,2 * N,2 * N)
temp[c,c] = 1
Hdiag += kron(temp,HSLG(vf,kx - qb[1],ky - qb[2],kk,jj,d,-theta/2)) # 2nd layer, blue points
c += 1
end
Hoff1 = zeros(ComplexF64,2 * N,2 * N) # off-diagonal element
Hoff2 = zeros(ComplexF64,2 * N,2 * N)
for k2 in -tr:tr,j2 in -tr:tr,k1 in -tr:tr,j1 in -tr:tr
if k1 == k2 && j1 == j2
off1 = zeros(ComplexF64,N,N)
off1[(k1 + tr) * s + j1 + tr + 1,(k2 + tr) * s + j2 + tr + 1] = 1
Hoff1 += kron(off1,Tb)
off2 = zeros(ComplexF64,N,N)
off2[(k2 + tr) * s + j2 + tr + 1,(k1 + tr) * s + j1 + tr + 1] = 1
Hoff2 += kron(off2,Tb')
elseif k1 == k2 && j1 + 1 == j2
off1 = zeros(ComplexF64,N,N)
off1[(k1 + tr) * s + j1 + tr + 1,(k2 + tr) * s + j2 + tr + 1] = 1
Hoff1 += kron(off1,Ttr)
off2 = zeros(ComplexF64,N,N)
off2[(k2 + tr) * s + j2 + tr + 1,(k1 + tr) * s + j1 + tr + 1] = 1
Hoff2 += kron(off2,Ttr')
elseif k1 - 1 == k2 && j1 == j2
off1 = zeros(ComplexF64,N,N)
off1[(k1 + tr) * s + j1 + tr + 1,(k2 + tr) * s + j2 + tr + 1] = 1
Hoff1 += kron(off1,Ttl)
off2 = zeros(ComplexF64,N,N)
off2[(k2 + tr) * s + j2 + tr + 1,(k1 + tr) * s + j1 + tr + 1] = 1
Hoff2 += kron(off2,Ttl')
end
end
Hoff = kron([0 1;0 0],Hoff1) + kron([0 0;1 0],Hoff2)
H = Hdiag + Hoff
val= eigvals(H)
band[ii,:] = sort(val)
end
temp = (a->(@sprintf "%3.2f" a)).(ang)
fn1 = "band-theta=" * temp * ".dat"
f1 = open(fn1,"w")
x0 = (a->(@sprintf "%15.8f" a)).(1:length(Nx))
y0 = (a->(@sprintf "%15.8f" a)).(band)
writedlm(f1,[x0 y0],"\t")
close(f1)
end
#----------------------------------------------------------
@time band(1.05)
@time band(5.0)
@time band(0.5)
绘图程序
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
config = {
"font.size": 30,
"mathtext.fontset":'stix',
"font.serif": ['SimSun'],
}
rcParams.update(config) # Latex 字体设置
#---------------------------------------------------------
def scatterplot1(cont):
dataname = "band-theta=" + format(cont,'.2f') + ".dat"
# dataname = "band-theta=1.05.dat"
tit = "Twist angele is " + format(cont,'.2f') + "$^\degree$"
# da1 = "did-short.dat"
picname = os.path.splitext(dataname)[0] + ".png"
os.chdir(os.getcwd())# 确定用户执行路径
x0 = np.loadtxt(dataname)
plt.figure(figsize=(10,10))
plt.plot(x0[:,0], x0[:,1:-1], c = 'blue')
x0min = np.min(x0[:,0])
x0max = np.max(x0[:,0])
# y0min = np.min(x0[:,1])
# y0max = np.max(x0[:,1])
font2 = {'family': 'Times New Roman',
'weight': 'normal',
'size': 25,
}
plt.xlim(x0min,x0max)
plt.ylim(-0.15,0.15)
# plt.xlabel(r'$\phi_{R-L}/\pi$',font2)
plt.ylabel("$E$",font2)
plt.title(tit,font2)
# plt.yticks(fontproperties='Times New Roman', size = 15)
plt.xticks(fontproperties='Times New Roman', size = 15)
# plt.xticks([0,1,2],fontproperties='Times New Roman', size = 25)
# plt.yticks([-0.25,-0.15,0,0.15,0.25],fontproperties='Times New Roman', size = 25)
plt.yticks([-0.15,0,0.15],fontproperties='Times New Roman', size = 25)
plt.tick_params(axis='x',width = 2,length = 10)
plt.tick_params(axis='y',width = 2,length = 10)
ax = plt.gca()
ax.spines["bottom"].set_linewidth(1.5)
ax.spines["left"].set_linewidth(1.5)
ax.spines["right"].set_linewidth(1.5)
ax.spines["top"].set_linewidth(1.5)
plt.savefig(picname, dpi = 100, bbox_inches = 'tight',transparent = True)
plt.close()
#---------------------------------------------------------
if __name__=="__main__":
scatterplot1(1.05)
scatterplot1(0.5)
scatterplot1(5)