之前在实空间在未考虑Rashba自旋轨道耦合的情况下计算了Kane-Mele的边界态,在这里详细的推导一下它动量空间和实空间之间是怎么变换的,由于它是在六角点阵上,所以和四方点阵相比就有一定的复杂性,在这里一边学习如何在六角点阵上进行正倒空间的变换,同时考虑Rashba自旋轨道耦合,完全重复一下文章结果。
基本定义
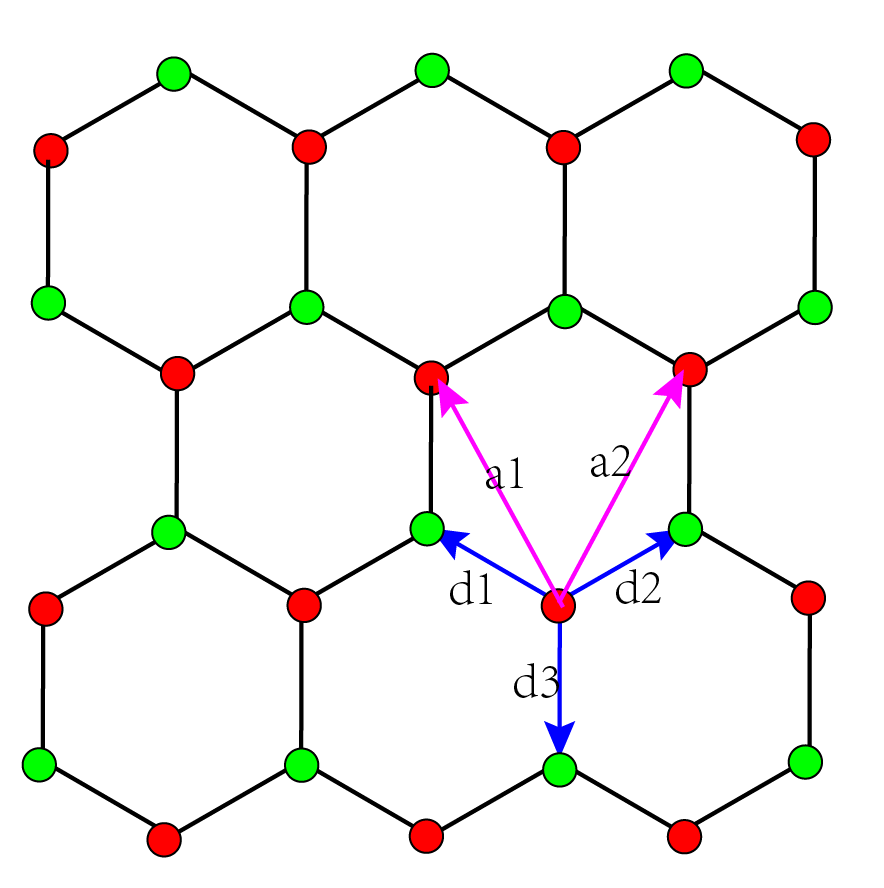
lattice vectors:$d_1=a(0,-1),d_2=a(-\sqrt{3}/2,1/2),d_3=a(\sqrt{3}/2,1)$,lattice平移矢量为$a_1=a(-\sqrt{3}/2,3/2),a_2=a(\sqrt{3}/2,3/2)$ ,平移矢量的长度为$\sqrt{3}a$,以这个长度为最小的单位。
Kane Mele模型的哈密顿量为
\[H=t \sum_{\langle i j\rangle} c_{i}^{\dagger} c_{j}+i \lambda_{S O} \sum_{\langle(i j)\rangle} v_{i j} c_{i}^{\dagger} s_{2} c_{j}+i \lambda_{R} \sum_{\langle i j\rangle} c_{i}^{\dagger}\left(\mathbf{s} \times \mathbf{d}\_{i j}\right)\_{z} c_{j}+\lambda_{v} \sum_{i} \epsilon_{i} c_{i}^{\dagger} c_{i}\]这里的每一个$c_i=(c_{i\uparrow},c_{i\downarrow})$都是二分量的形式,$v_{ij}=\frac{2}{\sqrt{3}}(\mathbf{d}_1\times\mathbf{d}_2)_z$,这一项中的$\mathbf{d}_i$代表的连接次近邻的矢量,不同的位置上会有符号的改变,充当的角色就是Haldane model中的位相。在这里也已经讨论过这一项的符号问题,可进行参考。
$\lambda_v\sum_i\epsilon_{i}c_i^\dagger c_i$
这一项中$\epsilon_i$对与a格点(红色)和b格点(绿色)是反号的,对于不同的自旋则都是相同的,且代表的是on-site的能量,所以从实空间转化到动量空间为
\[\lambda_v\sum_i\epsilon_{i}c_i^\dagger c_i=\lambda_v\Gamma_2\]$\Gamma_2=\sigma_zs_0$,这里$\sigma_z$ 正好代表了不同类型格点的符号是相反的,而$s_0$代表不同自旋是不会改变符号的,且写成矩阵形式的时候,基矢的选择为$\psi=(c_{a\uparrow},c_{b\uparrow},c_{a\downarrow},c_{b\downarrow})$,对于基矢选择与哈密顿量矩阵形式的问题,可以参考这里。
$t\sum_{\langle ij\rangle}c_i^\dagger c_j$
\[t\sum_{\langle ij\rangle}c_i^\dagger c_j\]通过上图可以看到,每个格点上都有3个最近邻位置,按照石墨烯哈密顿量构造中的方法,将这个实空间的形式变换到动量空间$\sum_k(e^{ikd_1} + e^{ikd_2} + e^{ik*d_3})$,利用关系$d_1=a_1+d_3,d_2=a_2+d_3$,则可以得到
\[\sum_ke^{ikd_3}(1+e^{ika_1}+e^{ika_2})=\sum_ke^{ikd_3}(\cos(ka_1)+\cos(ka_2)+i(\sin(ka_1)+\sin(ka_2)))\]利用关系表达$ka_1=y-x,ka_2=y+x,\cos(y-x)+\cos(y+x)=2\cos(x)\cos(y)$,$\sin(y+x)+\sin(y-x)=2\cos(y)\sin(x)$
最后的结果为:
\[t\sum_{<ij>}c^\dagger_ic_j\rightarrow t(1+2\cos(x)\cos(y))\Gamma_1-2t\cos(x)\sin(y)\Gamma_{12}\]$\Gamma_1=\sigma_x\otimes s_0,\Gamma_{12}=-\sigma_y\otimes s_0$
$i\lambda_{so}\sum_{\langle\langle ij\rangle\rangle}v_{ij}c^\dagger_is_zc_j$
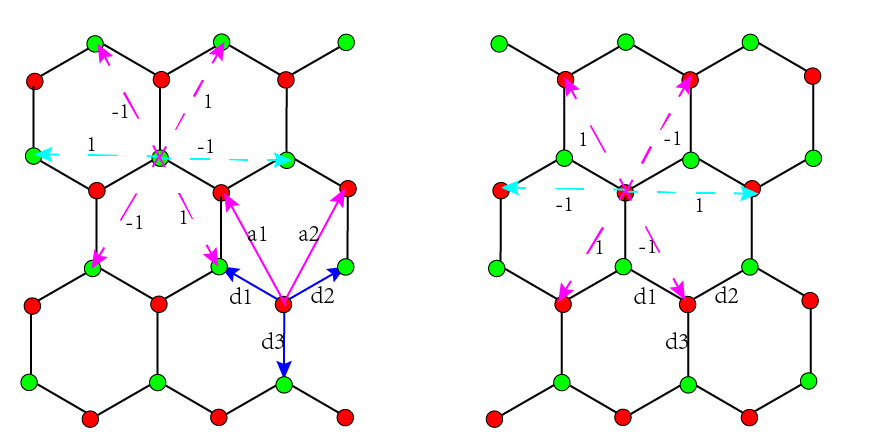
首先计算两个水平方向由青色箭头所示的次近邻hopping,这两个矢量的方向为$v_1=a_2-a_1,v_2=a_1-a_2$,$v_1$所示的hopping$v_{ij}=-1$,$v_2$所示的hopping$v_{ij}=1$ ,则这两项的结果为\(-e^{ikv_1}+e^{ikv_2}\),粉色箭头所示hopping反向正好是沿着平移矢量的方向,共有四项,$v_{ij}$的取值如上图所示,这四项的结果为
\(-e^{ika_1}+e^{ika_2}+e^{-ika_1}-e^{-ika_2}\),将这六项的结果加起来,然后利用关系$ka_2=y+x,ka_1=y-x,k*(a_1-a_2)=-2x$,可以得到$2i[2\cos(y)\sin(x)-\sin(2x)]$,自旋轨道耦合项前面本来就有一个虚数因子,将它吸收进来后,这一项变为$\lambda_{so}(2\sin(2x)-4\cos(y)\sin(x))\Gamma_{15}$,关于$\Gamma$矩阵的定义请自行参考文章。我在上面只展示了绿色原子的的次近邻hopping,对红色原子也可以进行同样的计算,即如上图中右侧标记所示,会发现它的结果和绿色原子正好相差一个负号,即可认为是不同轨道的次近邻是相反的,而且这一项中本来就存在$s_z$,基于此可以得到$\Gamma_{15}=\sigma_z\otimes s_z$ 。
$i\lambda_R\sum_{\langle ij\rangle}c^\dagger_i(\mathbf{s}\times \mathbf{d}_{ij})_zc_j$
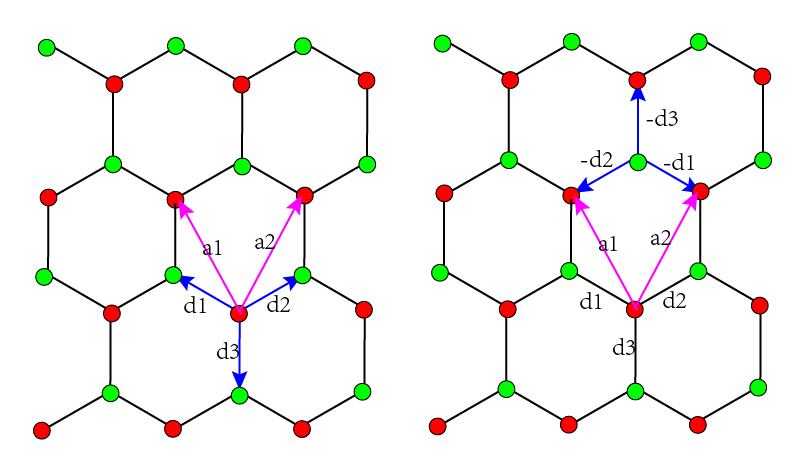
首先将三个三个最近邻的矢量$d_1,d_2,d_3$写成三维的矢量形式$d_1=(-\frac{\sqrt{3}}{2},\frac{1}{2},0),d_2=(\frac{\sqrt{3}}{2},\frac{1}{2},0),d_3=(0,-1,0)$,将上面表达式中的矢量叉乘展开则可以得到$s_x\cdot (d_{ij})y-s_y\cdot (d{ij})_x$,则接下来就这将最近邻的坐标代如计算每个最近邻的对于这个展开的表达式。将三个最近邻位置的矢量用平移矢量$d_1,d_2$表示出来$d_1=a_1+d_3,d_2=a_2+d_3$,然后计算每一个最近邻hopping的贡献。
- $\frac{1}{2}s_xe^{ik(a_1+d_3)}+\frac{\sqrt{3}}{2}s_ye^{ik(a_1+d_3)}$
- $\frac{1}{2}s_xe^{ik(a_2+d_3)}-\frac{\sqrt{3}}{2}e^{ik(a_2+d3)}$
- $-s_xe^{ikd_3}$
利用欧拉公式将上面三项展开后并组合到一起得到:
\[e^{ikd_3}[\frac{1}{2}s_x(\cos(ka_1)+\cos(ka_2)-2)+\frac{1}{2}is_y(\sin(ka_1)+\sin(ka_2))]\] \[+e^{ikd_3}[\frac{\sqrt{3}}{2}s_y(\cos(ka_1)-\cos(ka_2))+\frac{\sqrt{3}}{2}is_y(\sin(ka_1)-\sin(ka_2))]\]利用关系式:$ka_1=y-x,ka_2=y+x,\cos(y-x)+\cos(y+x)=2\cos(x)\cos(y),\sin(y-x)+\sin(y+x)=2\cos(x)\sin(y)$
$\cos(y-x)-\cos(y+x)=2\sin(x)\sin(y),\sin(y-x)-\sin(y+x)=-2\cos(y)\sin(x)$
最后整理结果为
\[e^{ikd_3}(s_x\cos(x)\cos(y)+s_xi\cos(x)\sin(y)-2s_x)+e^{ikd_3}(\frac{\sqrt{3}}{2}s_y\sin(x)\sin(y)-i\sqrt{3}s_y\cos(y)\sin(x))\]这里要说的是,上面的推导都是以上图为基础,即只是推导了红色原子的最近邻Rashba自旋轨道耦合,对蓝白色原子的推导过程和红色原子完全一样,唯一不同的是绿色原子的最近邻方向上的三个基矢和红色原子是反过来的,如上图右侧所示,所以结果会不同,可以认为这是轨道不简并所以在写成矩阵形式的时候,Rashba项对应的轨道的Pauli矩阵一定不会是$\sigma_0$
结语
到这里推导算是完成了,但是所有的结果只是在形式上和文章中符合,包括$\Gamma$矩阵到底是如何从实空间出发构建的并没有推导,而且我这里的结果是有一些不正常的地方,首先是关于次近邻的推到中,所有项都存在一个$e^{ikd_3}$的因子,我暂时不明白为什么这一项会一致存在,且在文章中并没有,但是推导过程我并没有找到自己的错误,我也会再看看推导来把这个位相因子解释清楚。
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |