在固体理论和量子场论的学习过程中都遇到了电极化函数的计算，在这里就详细的整理一下如何计算电子气中的电极化函数，这个计算有时候也成为RPA，当然这个方法并不仅限于计算电极化，还可以用来计算其它的一些量。

运动方程方法推导

假设在系统中放入一个杂质点电荷$\rho_i(\mathbf{r},t)$或这其傅里叶变换形式为$\rho_i(\mathbf{q},\omega)$,那么有这个电荷产生的等效势为$V_i(\mathbf{q},\omega)=-e\phi_i(\mathbf{q},\omega)$.一旦存在了杂质电荷之后,那么在其周围就会形成屏蔽电荷,从而也会产生一个额外的屏蔽势$V_s(\mathbf{q},\omega)$,则可以由一下方程

\[V(\mathbf{q},\omega)=V_i(\mathbf{q},\omega)+V_s(\mathbf{q},\omega)\] \[\nabla^2V_s(\mathbf{r},t)=4\pi e\rho_s(\mathbf{r},t)\qquad or\qquad V_s(\mathbf{q},\omega)=-\frac{4\pi e}{q^2}\rho_s(\mathbf{q},\omega)\] \[\nabla^2 V_i(\mathbf{r},t)=4\pi e\rho_i(\mathbf{r},t)\qquad or\qquad V_s(\mathbf{q},\omega)=-\frac{4\pi e}{q^2}\rho_i(\mathbf{q},\omega)\]

综上所述,可以知道由杂质电荷引起的势$V_i$是可以知道的,但是电子感受到的应该是$V(\mathbf{q},\omega)$,所以最终的问题就是如何求解这个总的势能,从而可以得到电极化函数

\[\epsilon(\mathbf{q},\omega)=\frac{V_i(\mathbf{q},\omega)}{V(\mathbf{q},\omega)}\]

电子的有效哈密顿量为

\[H=\sum_{\mathbf{p}\sigma}\epsilon_\mathbf{p} C^\dagger_{\mathbf{p}\sigma}C_{\mathbf{p}\sigma}+\frac{1}{v}\sum_\mathbf{q}V(\mathbf{q},t)\rho(\mathbf{q})\]

假设杂质是满足单频震动的$\qquad \rho_i(\mathbf{r},t)=\rho_i(\mathbf{r})e^{-i\omega t}\qquad V_i(\mathbf{r},t)=V_i(\mathbf{r})e^{-i\omega t}$,则系统的平均响应也是依赖于$\omega$的,$\langle \rho(\mathbf{q},t)\rangle=\rho(\mathbf{q},t)e^{-i\omega t}, \qquad \langle V(\mathbf{q},t)\rangle=V(\mathbf{q},\omega)e^{-i\omega t}$.对于均匀电子气,如果$\mathbf{q}\neq 0$,那么密度算符$\rho(\mathbf{q})$的期望值就是0,但是在杂质电荷存在时,其期望值不为0且正比于屏蔽电荷的平均值.

\[\langle \rho_s(\mathbf{q},t)\rangle = -e\langle\rho(\mathbf{q},t)\rangle=-e\sum_{\mathbf{p}\sigma}\langle C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p},\sigma}\rangle=-e\rho(\mathbf{q},\omega)e^{-i\omega t}\]

既然$\rho_s$和$\rho$是成正比的,那么整体上就可以有很大的简化,可以得到下面这个公式

\[V_s(\mathbf{q},\omega)=\frac{4\pi e^2}{q^2}\rho(\mathbf{q},\omega)\]

在这里其实是对电子电子相互作用的一个粗糙处理,这里是将电子电子相互作用简单的由屏蔽势($V_s(\mathbf{q},t)$)来描述,即电子电子相互作用导致了电荷周围吸引相反电性的电子,从而产生了屏蔽势.而在这整个问题中,需要求解的也就是$V_s(\mathbf{q},t)$,在前面的分析中我们已经得到了$V_s$与$\rho_s$之间的关系,又因为$\rho_s$和$\rho$之间又是正比的关系,所以现在的问题就转变成了$\rho(\mathbf{q},t)$的具体表达式到底是怎么样的.

下面就利用运动方程来求解$\rho(\mathbf{q},t)$的具体形式

\[i\frac{d}{dt}\rho(\mathbf{q},t)=[H,\rho(\mathbf{q},t)] \qquad \rho(\mathbf{q},t)=\sum_{\mathbf{q},\sigma}C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}\]

因为$\rho(\mathbf{q},t)$仅仅是对动量$\mathbf{q}$以及粒子内部自由度的求和,所以我们可以将求和分离开来,单独求解确定动量$\mathbf{q}$和内部自由度$\sigma$后的结果,之后再对这个量进行求和即可,所以问题转换为如何求解下面的表达式

\[i\frac{d}{dt}C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}=[H,C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}]\]

在线性屏蔽模型中,有$\langle \rho(\mathbf{q},t)\rangle\propto\langle V(\mathbf{q},t)\rangle$,杂质势$V(\mathbf{q},t)$是由一个振荡频率的$e^{-i\omega t}$,所以在对$\rho(\mathbf{q},t)$求导时,相当于只给出$-i\omega\sum_{\mathbf{p}\sigma}C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}$.

下面来计算哈密顿量于算符之间的对易关系

\[\sum_{\mathbf{k},s}\epsilon_\mathbf{k}[C^\dagger_{\mathbf{k}s}C_{\mathbf{k}s},C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}]=(\epsilon_\mathbf{p+q}-\epsilon_\mathbf{p})C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}\]

在上面的对易关系展开后不为零的两项为$\sum_{\mathbf{k}s}[C^\dagger_{\mathbf{k}s},C_{\mathbf{p}\sigma}]\sim-\epsilon_\mathbf{p}C^\dagger_{\mathbf{p+q}\sigma}C_{\mathbf{p}\sigma},\quad \sum_{\mathbf{k}s}[C_{\mathbf{k}s},C^\dagger_{\mathbf{p+q},\sigma}]\sim\epsilon_\mathbf{p+q}C^\dagger_{\mathbf{p+q}\sigma}C_{\mathbf{p}\sigma}$

在计算算符对易的时候,不同的两个动量指标$k,q$之间是需要满足一定限制的才可以,也可以简单的说这两个指标要相同它们才能满足对易关系,否则就是零.

对于包含库伦势的这一项

\[\frac{1}{v}\sum_{\mathbf{q'k},s}V(\mathbf{q'},t)[C^\dagger_{\mathbf{k+q'},s}C_{\mathbf{k}s},C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}]=\frac{1}{v}\sum_\mathbf{q'}V(\mathbf{q'},t)(C^\dagger_{\mathbf{p+q+q'}}C_{\mathbf{p}\sigma}-C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{\mathbf{p-q'},\sigma}})\]

在计算相互作用项与密度算符之间的对易关系时,同样使用算符下标之间的限制,最终就可以把求和的$\sum_k$消除,从而将不同的动量角标$p,q,k$联系起来.

将上面所有的计算结果回代,则可以得到

\[(\epsilon_\mathbf{p}-\epsilon_\mathbf{p+q}+\omega)C^\dagger_{p+q,\sigma}C_{\mathbf{p}\sigma}=\frac{1}{v}\sum_\mathbf{q'}V(\mathbf{q'},t)(C^\dagger_{\mathbf{p+q+q'},\sigma}C_{\mathbf{p}\sigma}-C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{\mathbf{p-q'},\sigma}})\]

下面开始做近似处理,也是RPA计算的关键.在上式的求和中,认为只有$\mathbf{q’}=-q$的贡献是最主要的,而其它的项则在平均之后相加等于0,这意思就是无规相近似的核心.这也说明这些被消去的项代表的是更高阶的相互作用.

\[\approx \frac{1}{v}V(\mathbf{q},t)(C^\dagger_{\mathbf{p}\sigma}C_{\mathbf{p}\sigma}-C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{\mathbf{p+q},\sigma}})\]

综上可以得到

\[C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}=\frac{V(\mathbf{q},t)}{v}(\frac{C^\dagger_{\mathbf{p}\sigma}C_{\mathbf{p}\sigma}-C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p+q},\sigma}}{\epsilon_\mathbf{p}-\epsilon_\mathbf{p+q}-\omega})\]

之后再对$(\mathbf{p},\sigma)$求和即可得到

\[\rho(\mathbf{p},t)=\sum_{\mathbf{p}\sigma}C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p}\sigma}=\frac{V(\mathbf{p},t)}{v}\sum_{\mathbf{p}\sigma}\frac{C^\dagger_{\mathbf{p}\sigma}C_{\mathbf{p}\sigma}-C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p+q},\sigma}}{\epsilon_\mathbf{p}-\epsilon_\mathbf{p+q}-\omega}\]

下面对这个方程求平均(量子期望值):$C^\dagger_{\mathbf{p}\sigma}C_{\mathbf{p}\sigma}\rightarrow n_F(\xi_{\mathbf{p}}),C^\dagger_{\mathbf{p+q},\sigma}C_{\mathbf{p+q},\sigma}\rightarrow n_F(\xi_{\mathbf{p+q}})$

对上面的方程取平均,$\langle \rho\rangle\rightarrow\rho(\mathbf{q},\omega)e^{-i\omega t},\quad \langle V\rangle\rightarrow V(\mathbf{q},\omega)e^{-i\omega t}$

\[\rho(\mathbf{q},\omega)=\frac{V(\mathbf{q},\omega)}{v}\sum_{\mathbf{p}\sigma}\frac{n_F(\xi_{\mathbf{p}})-n_F(\xi_{\mathbf{p+q}})}{\epsilon_{\mathbf{p}}-\epsilon_{\mathbf{p+q}}-\omega}=V(\mathbf{q},\omega)P^{(1)}(\mathbf{q},\omega)\]

将这个结果再回代到前面屏蔽势的表达式中可以得到

\[V_s(\mathbf{q},\omega)=\frac{4\pi e^2}{q^2}\rho(\mathbf{q},\omega)=V(\mathbf{q},\omega)v_qP^{(1)}(\mathbf{q},\omega)\]

到这里之后,又相互作用引起的屏蔽势已经可通过全库伦势能完全表示出来,剩下的问题就是将这些公式整合到一起,通过自洽的方式来的杂质势和全库伦势之间的联系

\[V(\mathbf{q},\omega)=V_i(\mathbf{q},\omega) + V_s(\mathbf{q},\omega)=V_i(\mathbf{q},\omega)+v_pV(\mathbf{q},\omega)=\frac{V_i(\mathbf{q},\omega)}{1-v_qP^{(1)}(\mathbf{q},\omega)}\]

则最终可以得到RPA计算电极化函数的结果

\[\epsilon_{RPA}=1 - v_qP^{(1)}(\mathbf{q},\omega)\] \[P^{(1)}(\mathbf{q},\omega) = \frac{1}{v}\sum_{\mathbf{q}\sigma}\frac{n_F(\xi_\mathbf{q}-n_F(\xi_\mathbf{p+q})}{\epsilon_\mathbf{p}-\epsilon_\mathbf{p+q}+\omega+i\delta}\]

格林函数方法推导

在这里不推到电极化函数到底是如何表示成格林函数形式的,具体的推到可以去看参考中的第一本书,这里直接将公式套用过来

\[\frac{1}{\epsilon(\mathbf{q})}=1-\frac{v_q}{V\beta}\int^\beta_0d\tau_1\int^\beta_0d\tau_2\langle T_\tau\rho(\mathbf{q},\tau_1)\rho(-\mathbf{q},\tau_2)\rangle\]

利用虚时间下的周期性条件,上式可以进行化简

\[\int^\beta_0d\tau_1\int^\beta_0d\tau_2\langle T_\tau\rho(\mathbf{q},\tau_1)\rho(-\mathbf{q},\tau_2)\rangle=\beta\int^\beta_0d\tau\langle T_\tau\rho(\mathbf{q},\tau)\rho(\mathbf{-q},0)\rangle\]

化简之后得到

\[\frac{1}{\epsilon(\mathbf{q})}=1-\frac{v_q}{V}\int^\beta_0d\tau\langle T_\tau\rho(\mathbf{q},\tau)\rho(\mathbf{-q},0)\rangle\]

上面的结果都是再零频率下的,接下来将这个结果推广到非零频率下

\[\frac{1}{\epsilon(\mathbf{q},i\omega_n)}=1-\frac{v_q}{V}\int^\beta_0d\tau e^{i\omega_n\tau}\langle T_\tau \rho(\mathbf{q},\tau)\rho(\mathbf{-q},0)\rangle\]

上面的推导都是在虚时的海森堡绘景中进行的,当把上面的结果转换到相互作用绘景中后,上式结果为

\[\frac{1}{\epsilon(\mathbf{q},i\omega)}=1-\frac{v_q}{V}\int^\beta_0d\tau e^{i\omega_n\tau}\frac{\langle T_\tau \hat{S}(\beta)\hat{\rho}(\mathbf{q},\tau)\hat{\rho}(-\mathbf{q},0)\rangle}{\langle\hat{S}(\beta)\rangle}\]

至于如何从海森堡绘景转换到相互作用绘景,在这里就不解释了,之后会整理一份三个不同绘景之间的联系

转换到相互作用绘景之后,可以发现这里存在一个$\hat{S}(\beta)$,其具体表达式为$S(\tau_1,\tau_2)=T_\tau exp[-\int_{\tau_1}^{\tau_2} d\tau_1\hat{V}(\tau_1)]$,这里$\hat{V}就是相互作用项在相互作用绘景中的形式$,下面对$\S(\beta)$的使用做一个示范

\[_0\langle T_{\tau}S(\beta)\hat{C}_{p\sigma}(\tau)\hat{C}^\dagger_{p\sigma}(0)\rangle=\sum^\infty_{n=0}\frac{(-1)^n}{n!}\int^\beta_0d\tau_1\dots\int^\beta_0d\tau_n(_0\langle T_\tau \hat{C}_{p\sigma}(\tau)\hat{V}(\tau_1)\dots\hat{V}(\tau_n)\hat{C}^\dagger_{p\sigma}(0)\rangle)\]

在现在这个问题中相互作用项为$V=\frac{1}{v}\sum_{pkq}\sum_{\sigma\sigma’}v_qC^\dagger_{p+q,\sigma}C^\dagger_{k-q,\sigma’}C_{k\sigma’}C_{p\sigma}$

在极化函数表达式中,将$S$展开到一阶可以得到$P^{(1)}(\mathbf{q},\omega)$

\[P^{(1)}=-\frac{1}{v}\int^\beta_0d\tau e^{i\omega_n\tau}\langle T_\tau \hat{\rho}(\mathbf{q},\tau)\hat{\rho}(-\mathbf{q},0)\rangle=-\frac{1}{v}\sum_\mathbf{kp}\sum_{\sigma\sigma'}\int^\beta_0d\tau e^{i\omega_n\tau}\langle T_\tau\hat{C}_{\mathbf{p}\sigma}(\tau)\hat{C}_{\mathbf{k-q},\sigma'}(0) \rangle\hat{C}_{\mathbf{k}\sigma'}(0)\hat{C}_{\mathbf{k}\sigma'}\\ =\frac{1}{v}\sum_{\mathbf{p}}\int^\beta_0d\tau e^{i\omega_n\tau}\mathcal{G}^{(0)}(\mathbf{p},\tau)\mathcal{G}^{(0)}(\mathbf{p+q},-\tau)=\frac{1}{v}\sum_{\mathbf{p}\sigma}\frac{n_F(\xi_\mathbf{p})-n_F(\xi_\mathbf{p+q})}{\epsilon_\mathbf{p}-\epsilon_\mathbf{p+q}+i\omega}\]

在最后一步的计算中使用了松原频率求和,可以参考这里.到这里之后,可以发现结果和运动方程求解得到的$P^{(1)}$是相同的(虚时格林函数进行解析延拓之后即可以得到实时间下的格林函数).计算到这里结束,虽然对于RPA还有很多可以讨论的内容,但是我再这里仅仅只是整理了一下它的计算方式和使用到的一些技巧.

场论方法推导

当从场论的角度出发来推导RPA的时候,最主要的是两个量,一个是action,另外一个是自由能.场论在推导到时候主要利用了微扰展开的方法,这部分内容可以参考Condensed Matter Field Theory的第五章,而RPA的推导也是在这一章,我仅仅是将主要的内容整理到一起,并加上一些自己的理解.

首先对于相互作用电子气,action为

\[S[\psi,\bar{\psi}]=\sum_p\bar{\psi}_{p\sigma}(-i\omega+\frac{\mathbf{p}^2}{2m}-\mu)\psi_{p\sigma}+\frac{T}{2L^3}\sum_{pp'q}\bar{\psi}_{p+q,\sigma}\bar{\psi}_{p'-q,\sigma'}V(\mathbf{q})\psi_{p'\sigma'}\psi_{p\sigma}\]

这里采用了简写$p\equiv(\mathbf{p},\omega_n)$,这里就不对一阶以及二阶围绕展开做讨论了,这不是现在这篇博客的关注点,我在这里直接计算n阶微扰展开

\[F^{(n)}_{RPA}=-\frac{T}{2n}\sum_q(\frac{2T}{L^3}V(\mathbf{q})\sum_pG_pG_{p+q})^n\]

如果从费曼图的角度来分析,在进行n阶微扰计算的时候,首先忽略那些贡献比较小的图,也可以简单的认为忽略那些在计算上不发散的图,保留这些计算上发散的图,然后对这些发散的图进行求和,最后可能得到一个不发散的结果,这个操作在格林函数的计算中是经常使用的,简单的图例如下

png

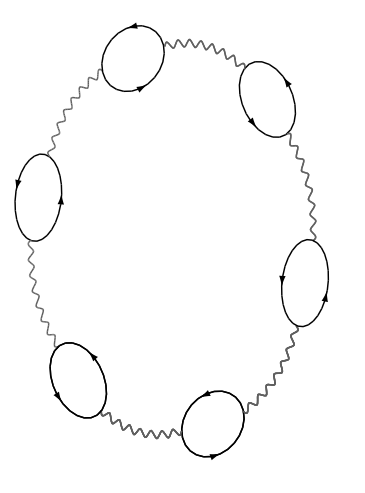
由上面的这个图可以看到,它都是由最小的bubble构成的,也正符合上面提到的求和的要求,经过计算就会发现对这种发散结构的求和最终居然可以得到一个收敛的结果,我一直觉得这是个比较怪异的事请,但是在计算上又确实没有问题.

下一步就是对所有阶数进行求和

\[F_{RPA}\equiv\sum_nF_{RPA}^(n)=\frac{T}{2}\sum_q\ln(1-V(\mathbf{q})\Pi_q)\qquad \Pi_q\equiv\frac{2T}{L^3}\sum_pG_pG_{p+q}\]

$G_p$是自由粒子的格林函数,可以很容易求解得到,则最终的结果为

\[\Pi_q=\frac{2T}{L^3}\sum_p\frac{1}{-i\omega_n+\xi_\mathbf{p}}\frac{1}{-i\omega_{n+m}+\xi_\mathbf{p+q}}=\frac{2}{L^3}\sum_\mathbf{p}\frac{n_F(\xi_\mathbf{p+q})-n_F(\xi_\mathbf{p})}{i\omega_m + \xi_\mathbf{p+q}-\xi_\mathbf{p}}\]

最后这个推导仍然是利用了松原求和技巧,Condensed Matter Field Theory$P_{170}$对这个技巧也有详细的推导和介绍,感兴趣可以进行参考.