格林函数的计算是在零温下进行的,但是实验却是再非零温下进行,那么就意味着实验观测中一定包含了热力学涨落,而这时候热力学统计物理这个工具就可以发挥作用了,自然的就需要利用松原格林函数来对有限温系统的格林函数进行计算,而零温时候的结果仅仅就是松原格林函数进行解析延拓即可,这里就主要展示一下松原格林函数的一些推导以及它与零温格林函数的联系是如何建立起来的.
热力学平均
首先定义关联函数
\[C_{AB}(t,t')=-\langle A(t)B(t')\rangle\]在这里$\langle\dots\rangle$是求期望值,如果是在非零温的情况下,那么求其统计平均为
\[C_{A B}\left(t, t^{\prime}\right)=-\frac{1}{Z} \operatorname{Tr}\left(e^{-\beta H} A(t) B\left(t^{\prime}\right)\right)\label{eq1}\]$Tr\equiv\sum_n\langle n\rvert\dots\rvert n\rangle$是一组完备基矢上的求和,接下来将(\ref{eq1})改写到相互作用绘景下,相互作用绘景的内容可以参考Schrodinger,Heisenberg,Interaction绘景的区别与联系这篇博客
\[C_{A B}\left(t, t^{\prime}\right)=-\frac{1}{Z} \operatorname{Tr}\left[e^{-\beta H} \hat{U}(0, t) \hat{A}(t) \hat{U}\left(t, t^{\prime}\right) \hat{B}\left(t^{\prime}\right) \hat{U}\left(t^{\prime}, 0\right)\right]\]在Schrodinger,Heisenberg,Interaction绘景的区别与联系中也提及到,利用相互作用绘景可以把有相互作用系统的基态与它无相互作用时的基态通过演化算符联系起来,从而达到在无相互作用基态上对物理量的求解,而这里进行这样的操作也是为了同样的目的.
虚时Heisenberg/Interaction 绘景
在这里再介绍一些虚时情况下的两种绘景.首先引进虚时完全就是一个数学的操作,是为了将统计物理中的$e^{\beta H}$与量子力学中的时间演化算符$e^{iHt}$在形式上可以进行统一,因为此时看上取好像一个是实数,另外一个则是复数,在进行$t\rightarrow i\tau$的变换后,此时$\tau$就是虚时间,那么从形式上来看$e^{\tau H}$和$e^{\beta H}$就都是实数的样子,而且这个时候也将温度$\beta=\frac{1}{k_B T}$和虚时间$it=\tau$联系了起来,这一点在松原格林函数中还是很重要的,具体它们之间是如何限制将在后面松原格林函数的性质讨论时展示.
在实时间Heisenberg绘景中
\[A(t)=e^{i t H} A e^{-i t H}\]进行虚时变换之后
\[A(\tau)=e^{\tau H} A e^{-\tau H}\]对应的相互作用绘景中的算符在虚时间下表示为
\[\hat{A}(\tau)=e^{\tau H_{0}} A e^{-\tau H_{0}}\]这里再次强调一下,这里的$H_0$是无相互作用时系统的哈密顿量.
有了上面的这些关系之后,那么同样可以将虚时Heisenberg算符改写成虚时Interaction绘景中的形式
\[A(\tau) B\left(\tau^{\prime}\right)=\hat{U}(0, \tau) \hat{A}(\tau) \hat{U}\left(\tau, \tau^{\prime}\right) \hat{B}\left(\tau^{\prime}\right) \hat{U}\left(\tau^{\prime}, 0\right)\label{eq4}\]虚时Interaction绘景下,演化算符为
\[\hat{U}\left(\tau, \tau^{\prime}\right)=e^{\tau H_{0}} e^{-\left(\tau-\tau^{\prime}\right) H} e^{-\tau^{\prime} H_{0}}\label{eq2}\] \[\begin{aligned} \hat{U}\left(\tau, \tau^{\prime}\right) &=\sum_{n=0}^{\infty} \frac{1}{n !}(-1)^{n} \int_{\tau^{\prime}}^{\tau} d \tau_{1} \cdots \int_{\tau^{\prime}}^{\tau} d \tau_{n} T_{\tau}\left(\hat{V}\left(\tau_{1}\right) \cdots \hat{V}\left(\tau_{n}\right)\right) \\ &=T_{\tau} \exp \left(-\int_{\tau^{\prime}}^{\tau} d \tau_{1} \hat{V}\left(\tau_{1}\right)\right) \end{aligned}\label{eq3}\]这里只是简单的将$it\rightarrow\tau$,其余的推导过程与Schrodinger,Heisenberg,Interaction绘景的区别与联系中完全一致,就不做重复了.结合(\ref{eq2})和(\ref{eq3})之后,可以将热力学统计的因子$e^{\beta H}$进行改写
\[e^{-\beta H}=e^{-\beta H_{0}} \hat{U}(\beta, 0)=e^{-\beta H_{0}} T_{\tau} \exp \left(-\int_{0}^{\beta} d \tau_{1} \hat{V}\left(\tau_{1}\right)\right)\]在虚时下同样可以有算符的热力学平均
\[\left\langle T_{\tau} A(\tau) B\left(\tau^{\prime}\right)\right\rangle=\frac{1}{Z} \operatorname{Tr}\left[e^{-\beta H} T_{\tau} A(\tau) B\left(\tau^{\prime}\right)\right]\]利用(\ref{eq4})其在相互作用绘景下的形式可得
\[\left\langle T_{\tau} A(\tau) B\left(\tau^{\prime}\right)\right\rangle=\frac{1}{Z} \operatorname{Tr}\left[e^{-\beta H_{0}} \hat{U}(\beta, 0) T_{\tau}\left(\hat{U}(0, \tau) \hat{A}(\tau) \hat{U}\left(\tau, \tau^{\prime}\right) \hat{B}\left(\tau^{\prime}\right) \hat{U}\left(\tau^{\prime}, 0\right)\right)\right]\]这里利用$Tr$的轮换不变性$Tr[ABC\dots YZ]=Tr[BC\dots YZA]$以及$\hat{U}\left(\tau, \tau^{\prime \prime}\right) \hat{U}\left(\tau^{\prime \prime}, \tau^{\prime}\right)=\hat{U}\left(\tau, \tau^{\prime}\right)$,以及$Z=\operatorname{Tr}\left[e^{-\beta H}\right]=\operatorname{Tr}\left[e^{-\beta H_{0} \hat{U}(\beta, 0)}\right]$可以得到
\[\left\langle T_{\tau} A(\tau) B\left(\tau^{\prime}\right)\right\rangle=\frac{1}{Z} \operatorname{Tr}\left[e^{-\beta H_{0}} T_{\tau} \hat{U}(\beta, 0) \hat{A}(\tau) \hat{B}\left(\tau^{\prime}\right)\right]=\frac{\left\langle T_{\tau} \hat{U}(\beta, 0) \hat{A}(\tau) \hat{B}\left(\tau^{\prime}\right)\right\rangle_{0}}{\langle\hat{U}(\beta, 0)\rangle_{0}}\]从上面的结果可以看到,在虚时绘景下,由成功的把问题转换到了在无相互作用哈密顿量本征态上的计算.
松原格林函数的定义
虚时格林函数的定义是利用虚时Heisenberg算符进行的
\[\mathcal{C}_{A B}\left(\tau, \tau^{\prime}\right) \equiv-\left\langle T_{\tau}\left(A(\tau) B\left(\tau^{\prime}\right)\right)\right\rangle\]编时算符展开对于Fermion与Boson是不同的
\[T_{\tau}\left(A(\tau) B\left(\tau^{\prime}\right)\right)=\theta\left(\tau-\tau^{\prime}\right) A(\tau) B\left(\tau^{\prime}\right) \pm \theta\left(\tau^{\prime}-\tau\right) B\left(\tau^{\prime}\right) A(\tau), \quad\left\{\begin{array}{c} +\text { for bosons } \\ -\text { for fermions. } \end{array}\right.\]在前面提到过,在虚时下$\tau$与$\beta$之间建立了联系,那么$\tau$的取值也就有了一定的限制,首先证明松原格林函数只不过是虚时差的函数,即$C_{AB}(\tau,\tau’)=C_{AB}(\tau-\tau’)$
\(\begin{aligned} \mathcal{C}_{A B}\left(\tau, \tau^{\prime}\right) &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} e^{\tau H} A e^{-\tau H} e^{\tau^{\prime} H} B e^{-\tau^{\prime} H}\right] \\ &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} e^{-\tau^{\prime} H} e^{\tau H} A e^{-\tau H} e^{\tau^{\prime} H} B\right] \\ &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} e^{\left(\tau-\tau^{\prime}\right) H} A e^{-\left(\tau-\tau^{\prime}\right) H} B\right] \\ &=\mathcal{C}_{A B}\left(\tau-\tau^{\prime}\right) \end{aligned}\) 这里仅仅使用了Tr的轮换性
松原格林函数重要的限制是$-\beta<\tau-\tau^{\prime}<\beta$时,才能保证$C_{AB}(\tau,\tau’)$是收敛的,因为仅从形式上看,如果虚时不在这个区间内,那么$Tr$内会出现$e^x(x>0)$这种形式,很可能会导致发散.
松原格林函数还具有周期性$C_{AB}(\tau)=\pm C_{AB}(\tau+\beta)\qquad for\quad \tau<0$
\[\begin{aligned} \mathcal{C}_{A B}(\tau+\beta) &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} e^{(\tau+\beta) H} A e^{-(\tau+\beta) H} B\right] \\ &=\frac{-1}{Z} \operatorname{Tr}\left[e^{\tau H} A e^{-\tau H} e^{-\beta H} B\right] \\ &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} B e^{\tau H} A e^{-\tau H}\right] \\ &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} B A(\tau)\right] \\ &=\pm \frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} T_{\tau}(A(\tau) B)\right] \\ &=\pm \mathcal{C}_{A B}(\tau) \end{aligned}\label{per}\]同样这里只利用了$Tr$的轮换性
既然函数具有周期性,那么就一定可以和傅里叶变换联系起来,虚时$\tau$限制在$[-\beta,\beta]$区间内,则其傅里叶变换有
\[\begin{array}{l} \mathcal{C}_{A B}(n) \equiv \frac{1}{2} \int_{-\beta}^{\beta} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau) \\ \mathcal{C}_{A B}(\tau)=\frac{1}{\beta} \sum_{n=-\infty}^{\infty} e^{-i \pi n \tau / \beta} \mathcal{C}_{A B}(n) \end{array}\]再利用(\ref{per})的周期性可得
\[\begin{aligned} \mathcal{C}_{A B}(n) &=\frac{1}{2} \int_{0}^{\beta} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau)+\frac{1}{2} \int_{-\beta}^{0} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau) \\ &=\frac{1}{2} \int_{0}^{\beta} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau)+e^{-i \pi n} \frac{1}{2} \int_{0}^{\beta} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau-\beta) \\ &=\frac{1}{2}\left(1 \pm e^{-i \pi n}\right) \int_{0}^{\beta} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau) \end{aligned}\]前面的因子$(1\pm e^{-i\pi n}$的值是由$n$来决定的,于是可以得到
\[\mathcal{C}_{A B}(n)=\int_{0}^{\beta} d \tau e^{i \pi n \tau / \beta} \mathcal{C}_{A B}(\tau), \quad\left\{\begin{array}{l} n \text { is even for bosons } \\ n \text { is odd for fermions } \end{array}\right.\]在这里进行一下符号的修改
\[\mathcal{C}_{A B}\left(i \omega_{n}\right)=\int_{0}^{\beta} d \tau e^{i \omega_{n} \tau} \mathcal{C}_{A B}(\tau), \quad\left\{\begin{array}{ll} \omega_{n}=\frac{2 n \pi}{\beta}, & \text { for bosons } \\ \omega_{n}=\frac{(2 n+1) \pi}{\beta}, & \text { for fermions. } \end{array}\right.\]$\omega_n$就是松原频率,对于费米子和玻色子,其取值是不同的.
松原格林函数与推迟格林函数
在频率域中,这松原格林函数与推迟格林函数是拥有相同的解析函数的,也就是说存在一个函数$C_{AB}(z)$,$z$是上面平面的复频率,如果$z$恰好在虚轴上那就是$C_{AB}(i\omega)$,如果是在实轴上就是$C^R_{AB}(\omega)$.这个关系告诉我们,只要知道了这两个其中的一个,那么另外一个可以通过解析延拓的方式得到.这也就是推迟格林函数与松原格林函数之间最重要的关系.$C^R_{AB}(\omega)=C_{AB}(i\omega_n\rightarrow \omega+i\eta)$,$\eta$是个无穷小量保证函数不会发散.
下面来利用Lehmann表示展示一下这两者之间的联系,首先对于$\tau>0$有
\[\begin{aligned} \mathcal{C}_{A B}(\tau) &=\frac{-1}{Z} \operatorname{Tr}\left[e^{-\beta H} e^{\tau H} A e^{-\tau H} B\right] \\ &=\frac{-1}{Z} \sum_{n n^{\prime}} e^{-\beta E_{n}}\left\langle n|A| n^{\prime}\right\rangle\left\langle n^{\prime}|B| n\right\rangle e^{\tau\left(E_{n}-E_{n^{\prime}}\right)} \end{aligned}\]$Tr\equiv\sum_n\langle n \rvert \dots \rvert n\rangle$,$\rvert n\rangle$是$H$的本征态,则可以得到上面的关系,接下来进行虚时到虚频的傅里叶变换
\[\begin{aligned} \mathcal{C}_{A B}\left(i \omega_{n}\right) &=\int_{0}^{\beta} d \tau e^{i \omega_{n} \tau} \frac{-1}{Z} \sum_{n n^{\prime}} e^{-\beta E_{n}}\left\langle n|A| n^{\prime}\right\rangle\left\langle n^{\prime}|B| n\right\rangle e^{\tau\left(E_{n}-E_{n^{\prime}}\right)} \\ &=\frac{-1}{Z} \sum_{n n^{\prime}} e^{-\beta E_{n}} \frac{\left\langle n|A| n^{\prime}\right\rangle\left\langle n^{\prime}|B| n\right\rangle}{i \omega_{n}+E_{n}-E_{n^{\prime}}}\left(e^{i \omega_{n} \beta} e^{\beta\left(E_{n}-E_{n^{\prime}}\right)}-1\right) \\ &=\frac{-1}{Z} \sum_{n n^{\prime}} e^{-\beta E_{n}} \frac{\left\langle n|A| n^{\prime}\right\rangle\left\langle n^{\prime}|B| n\right\rangle}{i \omega_{n}+E_{n}-E_{n^{\prime}}}\left(\pm e^{\beta\left(E_{n}-E_{n^{\prime}}\right)}-1\right) \\ &=\frac{1}{Z} \sum_{n n^{\prime}} \frac{\left\langle n|A| n^{\prime}\right\rangle\left\langle n^{\prime}|B| n\right\rangle}{i \omega_{n}+E_{n}-E_{n^{\prime}}}\left(e^{-\beta E_{n}}-(\pm) e^{-\beta E_{n^{\prime}}}\right) \end{aligned}\]从这里就可以得到一个在复平面上定义的函数
\[C_{A B}(z)=\frac{1}{Z} \sum_{n n^{\prime}} \frac{\left\langle n|A| n^{\prime}\right\rangle\left\langle n^{\prime}|B| n\right\rangle}{z+E_{n}-E_{n^{\prime}}}\left(e^{-\beta E_{n}}-(\pm) e^{-\beta E_{n^{\prime}}}\right)\]对松原格林函数进行解析延拓之后也就可以得到推迟格林函数,它们的联系也可以通过图像展示
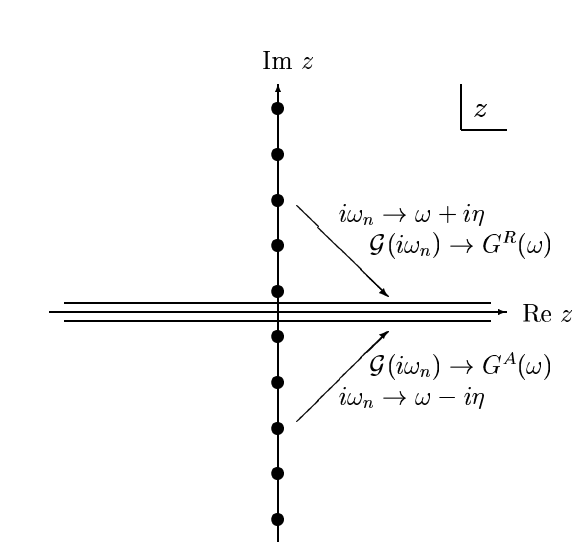
这里顺便再多说一句,$i\omega_n\rightarrow \omega+i\eta$是推迟格林函数,这个函数是再上半复平面的,当$i\omega_n\rightarrow \omega-i\eta$时得到就是超前格林函数,它是在下半复平面的,也就如上图所示
参考
- 1.Many body quantum theory in condensed matter physics
- 2.Many particle physics
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |