在固体物理的学习过程中,始终都要接触费米面这个概念,经常在学习理论知识,对实验的关注还是有些少,这里就整理一下实验上通过De Hass-Van Alphen效应测量费米面的一些理论知识,正好也梳理一下实验上的一些手法.
电子在磁场中的运动
准经典分析
这里先从准经典角度整理一下电子点外加磁场中是如何运动的.
\[\mathbf{v}(\mathbf{k})=\frac{1}{\hbar}\nabla_\mathbf{k}E(\mathbf{k})\\ \hbar\frac{d\mathbf{k}}{dt}=(-q)\mathbf{v}_k\times \mathbf{B}\]从上面的两个方程中可以有两个结论:
-
电子波矢$\mathbf{k}$沿着磁场方向是不随时间改变的,这点从第二个方程中可以得到,因为方程右端是速度和磁场的叉乘,结果中矢量的方向一定会同时垂直与速度和磁场的方向.
-
电子的能量$E(\mathbf{k})$是不会随时间变化的,也就是说电子始终在等能面上运动,这是因为磁场给电子的力是洛伦兹力,它是不会做功的,那么自然能量不会变化,电子就一直在等能面上运动.
量子分析
在不加磁场时,自由电子哈密顿量为$H=\frac{\mathbf{p}}{2m}=-\frac{\hbar^2}{2m}\nabla^2$,加入磁场之后,只要把动量$\mathbf{p}$替换成正则动量$\mathbf{p}+q\mathbf{A}$即可
\[H=\frac{1}{2m}(\mathbf{p}+q\mathbf{A})\]假设磁场是沿着z方向的,取朗道规范$\mathbf{A}=(-By,0,0)$,则哈密顿量可以写成
\[H=\frac{1}{2m}[(\hat{p}_x-qBy)^2+\hat{p}_y+\hat{p}_z]\]关于这个哈密顿量的求解可以参考固体物理$P_259$这也是一个标准的量子力学问题,最后可以求解得到随y变化部分波函数为
\[\varphi_n(y-y_0)\sim e^{-\frac{\omega_0}{2}(y-y_0)^2}H_n[\omega_0(y-y_0)]\]这里$y_0=\frac{\hbar}{qB}k_x,\omega_0=\frac{qB}{m}$,这是一个中心在$y_0$,振动频率为$\omega_0$的谐振子波函数,$H_n$是厄密多项式.则最后总的波函数为$\psi=e^{i(k_xx+k_zz)}\varphi_n(y-y_0)$.上面的计算表明,在$x-y$平面内的圆周运动对应着一种简写运动,能量是量子化的,这些量子化的能级称谓朗道能级,$E=\frac{\hbar^2 k_z^2}{2m}+(n+\frac{1}{2})$.
De Hass-Van Alphen效应
在强磁场中研究样品磁化率的时候,实验上发现磁化率随着磁场的变化会呈现出振荡,这个现象在很多材料中都存在,磁化率随磁场倒数$\frac{1}{B}$周期性振荡的现象称为De Hass-Van Alphen效应.这些现象是与金属费米面附近的电子在强磁场中的行为有关,所以它和金属费米面的结构也有密切的关系,通过这个效应可以对材料的费米面结构进行一定的探测.
自由电子气模型
二维自由电子气的色散关系为
\[E(\mathbf{k})=\frac{\hbar^2k^2}{2m}\qquad k^2=k_x^2+k_y^2\]如果在z方向加入磁场之后,那么$x-y$面内则会形成一系列离散的能级
\[E_n=(n+\frac{1}{2})\hbar\omega\]加入磁场之后,原本连续的能级编程了间隔为$\hbar\omega$的分离能级,可以把加入磁场后的过程看作无磁场时量子态的一个重组,但是在重组过程中,系统总的量子态数目时保持不变的,那么自然的每个朗道能级上对应的量子态数目是有很多的,也就是说朗道能级是高度简并的,每个朗道能级上包含的量子态数目就是原来连续能谱中能量间隔$\hbar\omega$内的量子态的数目,下图可以帮助理解
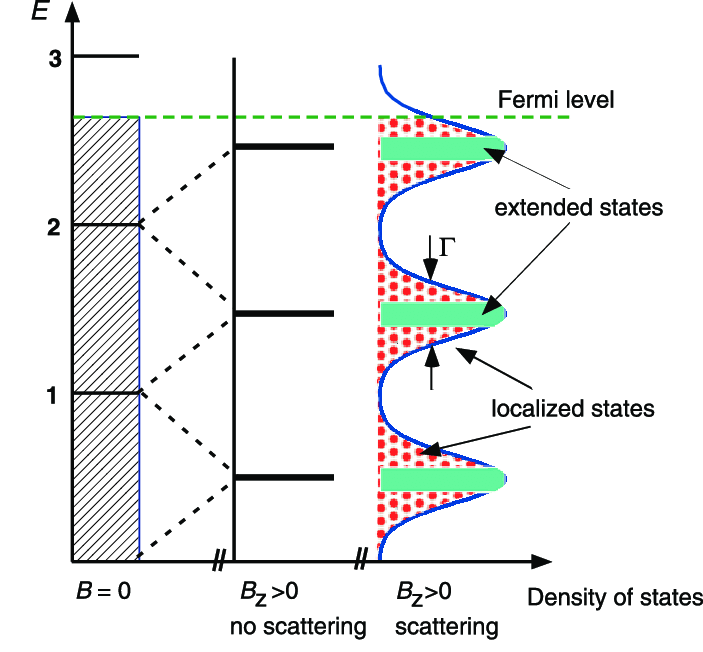
假设二维电子气所在的平面尺寸为$L\times L$,那么可以计算得到二维自由电子气的态密度为$\frac{mL^2}{\pi\hbar^2}$,从而可以计算得到每个朗道能级的简并度为
\[D=\frac{mL^2}{\pi\hbar^2}\times\hbar\omega=\frac{L^2q}{\pi\hbar}B\]下面从更加物理的角度来对朗道能级的简并度进行一个解释,前面我们已经知道,在垂直的磁场平面内,电子做简谐运动,满足波动方程
\[[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial y^2}+\frac{m}{2}\omega_0^2(y-y_0)]\phi(y)=\epsilon_1\phi(y)\]旋转中心$y_0=\frac{\hbar}{qB}k_x$,它的取值应该在L范围内,另外由边界条件$k_x$的取值是均匀的,其间隔为$\Delta k_x=\frac{2\pi}{L}$,所以可以求得$y_0$的间隔$\Delta y_0=\frac{\hbar}{qB}\times\frac{2\pi}{L}$,$y_0$的取值数为$\frac{L}{\Delta y_0}=\frac{L^2qB}{2\pi\hbar}$,如果考虑自旋,那么将这个量乘以2之后,就可以得到朗道能级的简并度.
在磁场中,形成一系列高度简并的分立能级,使得电子气系统能量将随着磁场强度B发生变化,这就是产生De Hass-Van Alphen效应的原因.
接下来对变化周期进行讨论,以$\frac{1}{B}$为变量.设磁场强度为$B_1$时,第$\lambda$能级恰好填满
\[\lambda D = N\\ \lambda\frac{L^2q}{\pi\hbar}B_1 = N\\ \frac{1}{B_1}=\lambda\frac{L^2q}{\pi\hbar N}\]设磁场强度为$B_2$时,第$(\lambda + 1)$能级恰好完全填满
\[(\lambda + 1)D = N\\ \frac{1}{B_1} = (\lambda + 1)\frac{L^2q}{\pi\hbar N}\] \[\Delta(\frac{1}{B})=(\frac{1}{B_1} - \frac{1}{B_2})=\frac{L^2q}{\pi\hbar N}=\frac{2\pi q}{\hbar S_F}\qquad S_F = 2\pi^2\frac{N}{L^2}\]$S_F$是二维自由电子气费米圆的面积,$S_F = 2\pi^2K^2_F$.在$T=0K$时,N个自由电子填充费米圆
\[2\times\frac{L^2}{(2\pi)^2}\times\pi K_F^2=N\]所以可以得到$S_F=2\pi^2\frac{N}{L^2}$.在绝对零度下系统的磁矩$M=-\partial E/\partial B$,上面分析得到$\Delta E$随$\frac{1}{B}$成周期变化,变化周期为$\frac{2\pi q}{\hbar S_F}$,所以此举也会随$\frac{1}{B}$成周期变化,与前面的变化周期相同.实验上就可以通过测量磁矩M随$\frac{1}{B}$变化的周期,从而来得到费米面$S_F$的信息.
实验结果
现在考虑在样品上施加固定的磁场$B_0$,那么振荡周期为
\[\Delta(\frac{1}{B_0})=\frac{2\pi e}{\hbar S_F}\]其中$S_F$是费米面与磁场形成的有效投影截面,前面的理论分析中实际上是以自由电子气为模型,并没有涉及到费米面存在简并的情形。因此在具体分析的时候还需要考虑到费米面是否存在简并。
在知道了振荡周期之后,自然可以得到电子的振荡频率
\[f_{B_0}=\frac{\hbar S_F}{2\pi e}\]可以看到除了费米面与磁场的有效截面$S_F$是变量之外,其它的量都是基本单位量。因此$S_F$与电子振荡频率$f_{B_0}$之间是线性关系的。
在固定磁场大小$B_0$的时候,改变体系中的电子填充,即可以调节费米面的位置,从而实现调控$S_F$的大小,如下图所示
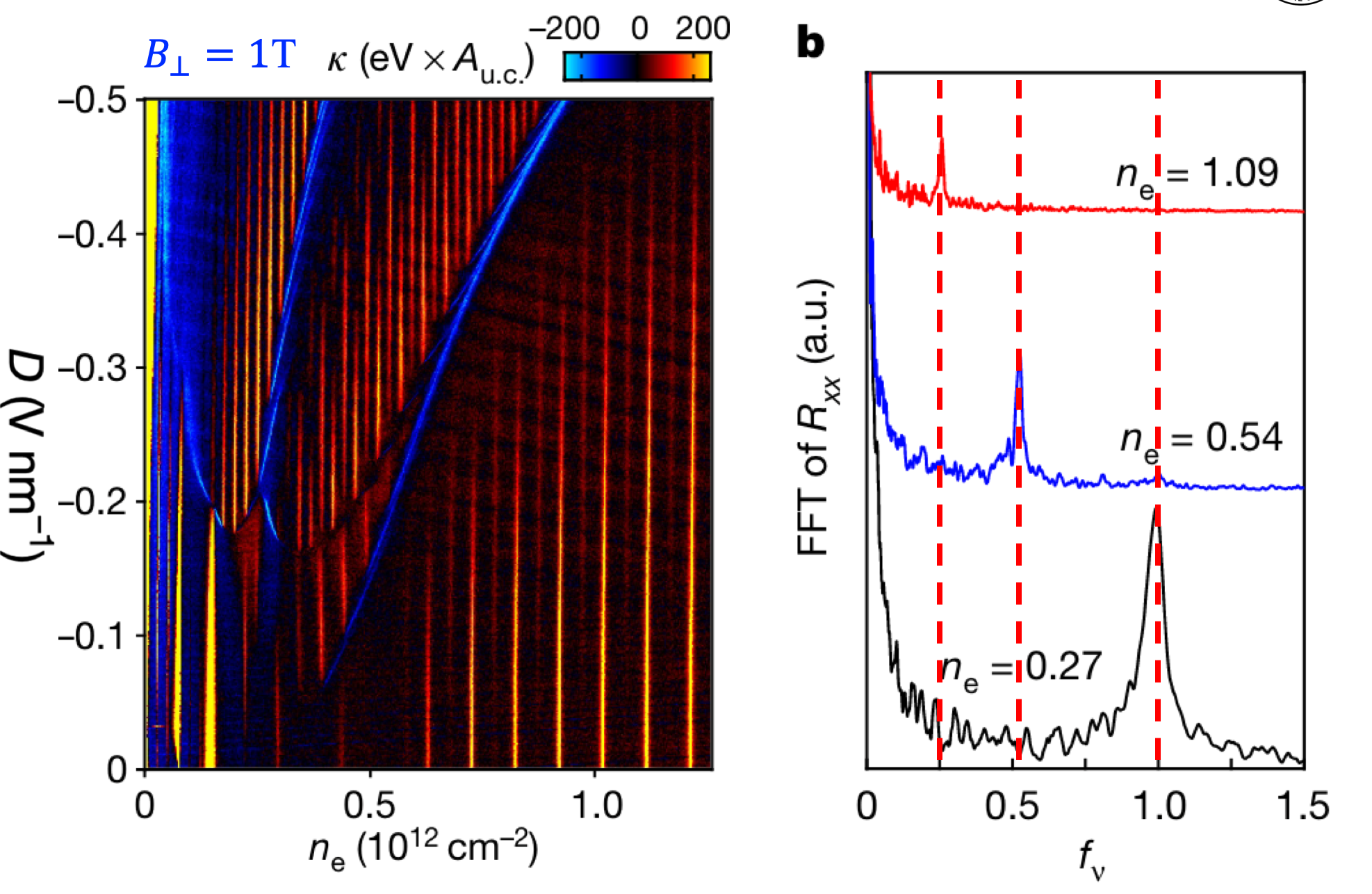
可以看到在不同的$n_e$下电子振荡频率之间存在倍数关系,从而在不同填充$n_e$的时候,它们费米面的简并度或者截面面积$S_F$之间也必然存在倍数关系(图片来源文章中研究的是费米面的简并度)。
参考
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |