在这里主要整理记录一些平时在推导中可能会用到的一些公式,以及在做计算时遇到的一些小技巧,因为时间长了可能对细节问题会忘记,所以整理在这里也可以很方便的进行查阅,同时在整理的过程中也是自己对这些知识的进一步理解。
T矩阵方法介绍
纯净系统的哈密顿量为$H^0(\bf{k})$,加入杂质$V$后,系统的哈密顿量为$H(\bf{k}) = H^0(\bf{k}) + V$。
加入杂质后系统的格林函数为\(G = G^0 + G^0 T G^0\),此处$G^0$代表纯净系统的格林函数:$G^0(z) = (z-H(\bf{k}))^{-1}$,$T$矩阵可以通过杂质$V$和$G^0$计算得到:$T=V(I-G^0V)^{-1}$,$I$代表单位矩阵。
对于点状杂质,通常是是写在实空间中的表达式$V(r)=V_0\delta(\bf{r})$,那么实空间中的格林函数为:$G(r,r’) = G^0(r,r’) + G^0(r,0)T_0(z)G^0(0,r’)$,在实空间中局域的$T_0$矩阵为$T_0(z) = (V^{-1} - G^0(z))^{-1}$,$G^0(z)=\frac{1}{N}\sum_k(z-H_k^0)^{-1}$,它是纯净系统动量空间中的格林函数的傅里叶变换,公式中的N代表傅里叶变换时选取的k点的数目。
参考文献
1.Impurity-induced states in conventional and unconventional superconductors
实空间与k空间Fourier变换
在固体物理的研究中通常要使用到紧束缚近似模型,而且还会用到它的实空间和k空间Hamiltonian,通常取晶格常数a=1,则实空间与k空间算符的变换关系为
$c_{k}=\frac{1}{\sqrt{2\pi}}\sum_jc_je^{-ikj}$
$c_j=\frac{1}{\sqrt{2\pi}}\int_{BZ}dkc_ke^{ikj}$
由于k空间是连续的,所以对动量k的积分是在整个第一布里渊区(BZ)进行的,而实空间的格点是离散的,所以由实空间算符到k空间算符进行的是离散的傅里叶变化,对应的由动量空间(k空间)到实空间的算符变化,进行的是连续傅里叶变换。
在此处需要说明的是,假设上面进行变换的算符都是费米子算符,则实空间与k空间的算符都是满足反对易关系的,在验证这个对易关系的时候,通常都要使用到$\delta$函数,它也同样有离散和连续的表达式
$\sum_j\frac{1}{2\pi}e^{-i(k-k’)j}=\delta(k-k’)$
$\frac{1}{2\pi}\int_{BZ}dke^{ik(x_i-x_j)}=\delta_{ij}$
若想将实空间中的Hamiltonian变换到k空间,则将$c_j$到$c_k$的变换关系代入,然后利用$\delta$函数的关系即可.同样的,由k空间变换到实空间的操作只不过是一个相反的过程,将本来的$c_k$写成由$c_j$的表示形式,然后利用$\delta$函数的关系即可.
通常,如果遇到实空间是个离散的晶格点阵,如果我们的体系在考虑的时候,并不是无限大的,那么对应着的k空间中的动量点k也是一些离散的量.假设取实空间的格点数为N,晶格常数为a,则实空间中系统的大小为L=N*a(为了简答考虑,先默认这个是一维的系统),则k点的取值为$k_m=\frac{2\pi m}{L}$,m的取值范围和N有关:$m=-\frac{N}{2},-\frac{N}{2}+1,…\frac{N}{2}-1$.这种离散的情况下通常进行实空间与动量空间变换时同样需要$\delta$函数的辅助
$\frac{1}{N}\sum_ke^{-ikj}e^{-ikj’}=\delta_{jj’}$
$\frac{1}{N}\sum_je^{ikj}e^{-ik’j}=\delta_{kk’}$
微分方程通解
\(H_{1}\left(-i \partial_{x}, k_{y}, k_{z}\right)=\left(\tilde{m}-\frac{t}{2} \partial_{x}^{2}+\frac{t}{2} k_{y}^{2}+\frac{t_{3}}{2} k_{z}^{2}\right) \sigma_{z}-i t^{\prime} \partial_{x} \sigma_{x} s_{z}\)
采用边界条件为$\psi_\alpha(0)=\psi_\alpha(\infty)=0$,求解本征方程$H_1\psi=E_\alpha\psi$,对于x=0处的零能解有两个
\[\psi_{\alpha}=\mathcal{N} \sin \left(\kappa_{1} x\right) e^{-\left(\kappa_{2} x\right)} e^{i k_{y} y} e^{i k_{z} z} \chi_{\alpha}\]归一化系数$\mathcal{N}=2 \sqrt{\kappa_{2}\left(\kappa_{1}^{2}+\kappa_{2}^{2}\right) / \kappa_{1}^{2}}$
\[\kappa_{1}=\sqrt{\frac{-2 \tilde{m}-t k_{y}^{2}-t_{3} k_{z}^{2}}{t}-\left(\frac{t^{\prime}}{t}\right)^{2}}, \kappa_{2}=\frac{t^{\prime}}{t}\]波函数还要满足$\sigma_{y} s_{z} \chi_{\alpha}=-\chi_{\alpha}$
满足条件的推导
由于$\psi_\alpha$是$H_1$的本征态,对应的本征值为0,则Pauli矩阵的作用对象就是$\chi_\alpha$
\[(\sigma_zs_0-i\sigma_xs_z)\chi_\alpha=0\]最终目的就是要把括号中的表达式化简成一边是Pauli矩阵,另一边是常数,也就是本征方程的形式
\[\sigma_x\sigma_y=i\sigma_z,\sigma_i^2=1\]利用上面Pauli矩阵的性质可以得到
\[-i\sigma_x\sigma_ys_0-i\sigma_xs_z=0\]将两边的$-i\sigma_x$同时消去得到$\sigma_ys_0=-s_z$,然后在两边同时乘以$s_z$,则可以得到最终的结果
\[\sigma_ys_z=-1\]在这里要说明一下,$\sigma_i,s_i$代表的是不同的自由度,$\sigma_xs_y$这种形式代表的是直积,$-i\sigma_x\sigma_y$是同一个自由度Pauli矩阵,它们在一起是代表矩阵的乘积,所以才有了上面在等式两端同时除以$-i\sigma_x$的。
粒子数密度
在这里对我遇到的两种密度算符进行一个推导,虽然平时也经常看到,但是对其如何来的并未深究,这里通过二次量子化的方法来对这两个密度算符进行推导
首先,对于任一波函数可以在一个完备的基矢组上进行展开$\Psi(r)=\sum_\lambda a_\lambda\phi_\lambda(r),\Psi^\dagger(r)=\sum_\lambda a^\dagger_\lambda\phi^{*}_\lambda(r)$,在这里要说明一下$\Psi^\dagger$与$a^\dagger$满足相同的对易关系,即都是对易或者反对易,这与研究的体系时费米子还是玻色子有关,而且在这里我们默认了算符都是不含时的,或者可以认为都是同一时刻的算符。如果它们不是同一时刻的算符,那么对易关系就不再是上面这种简单的形式了。
将哈密顿量利用二次量子化算符写出来之后为
\[H=\int d^3r\Psi^\dagger\mathcal{H}\Psi=\sum_{\lambda\lambda'}a_\lambda^\dagger a_{\lambda'}\int\phi^*_\lambda(r)\mathcal{H}\phi_{\lambda'}(r)=\sum_{\lambda}\epsilon_\lambda a^\dagger_\lambda a_\lambda\]这里强调一下几个符号$\mathcal{H}$是哈密顿量密度,所以这里是它作用到波函数上对空间的积分,而$\phi^\dagger$是$H$的本征态,所以在$\mathcal{H}$作用之后对全空间积分则可以得到$\epsilon_\lambda$,这也就是上面公式所包含的意思。
粒子密度算符 \(\rho(r)=\Psi^\dagger(r)\Psi(r)=\sum_{\lambda\lambda'}a^\dagger_\lambda a_{\lambda'}\phi^*_\lambda(r)\phi_{\lambda'}(r)\)
粒子数算符即对粒子密度算符对空间的积分 $N=\int d^3r\rho(r)=\sum_\lambda a^\dagger_\lambda a_\lambda$(利用$\phi$的归一化条件)
将密度算符变换到动量空间$\rho(q)=\int d^3re^{-iqr}\rho(r)=\sum_{\lambda\eta}c_\lambda^\dagger c_\eta\int d^3r\phi_\lambda^*(r)\phi_\eta(r)e^{-iqr}$
如果取自由粒子表象,也就是说以平面波为基矢做任意波函数的展开,那么$\phi=e^{-ikr}$
$\int e^{ik_1r}e^{-ik_2r}e^{-iqr}d^3r=\int e^{i(k_1-k_2-q)}d^3 r=\delta(k_1-k_2-q)$(这里忽略了积分的系数,并不是严格推导)
结果中会有一个$\delta$函数限制波矢的取值,即$k_1=k_2+q$,最终结果为$\rho(q)=\sum_{k\sigma}c^\dagger_{k+q,\sigma}c_{k\sigma}$
电流密度算符
粒子流:$j_i(r)=\frac{1}{2mi}{\psi^\dagger(r)\nabla\psi(r)-\psi(r)\nabla\psi^\dagger(r)}$,将波函数利用二次量子化的基矢做展开可得到:
\[j_i(q)=\frac{1}{2mi}\sum_{\lambda\eta}c^\dagger_\lambda c_\eta\int d^3re^{-iqr}[\phi^\star_\lambda(r)\nabla\phi_\eta(r)-\phi_\eta(r)\nabla\phi^*_\lambda(r)]\]接下来对于自由粒子,取平面波基矢做展开
\[\phi^\star_\lambda(r)\nabla\phi_\eta(r)-\phi_\eta(r)\nabla\phi^\star_\lambda(r)=e^{-ik_1r}\frac{\partial}{\partial r}e^{ik_2r}-e^{ik_2r}\frac{\partial}{\partial r}e^{-ir_1r}=(ik_1+ik_2)e^{i(k_1-k_2)r}\]$\int d^3r(ik_1+ik_2)e^{i(k_1-k_2-q)}=i(k_1+k_2)\delta(k_1-k_2-q)$ 利用$\delta$函数的限制之后,得到$k_1,k_2$之间的关系为$k_1=k_2+q$
最终结果为:$j_i(q)=\frac{1}{m}\sum_{k\sigma}(k+\frac{1}{2}q)c^\dagger_{k+q,\sigma}c_{k\sigma}$
泡里矩阵幺正变换
之前在文章中看到对哈密顿量进行幺正变换,可以将本来是$\sigma_x$的项变换到$\sigma_z$或者$\sigma_y$的表示下,这里整理一下这个幺正变换矩阵是如何进行操作的,首先想说明一下,我并不知道这个幺正变换如何寻出,但是发现这个变换矩阵是由$\sigma_y$的本征态构成的,应该是与定义矩阵时候的本征基矢相关,因为一般都是选取$\sigma_z$是对角形式,那么要变换泡里矩阵其实也就是意味着要以其它的泡里矩阵为基矢,也就是说以$\sigma_x$或者$\sigma_y$为对角形式,所以这个时候的幺正变换矩阵就应该是由其本征矢量来构建,矩阵形式为
\[\begin{equation}U=\frac{1}{\sqrt{2}}\left[\begin{array}{cc} i&-i\\ 1&1 \end{array}\right]\end{equation}\] \[U\cdot\sigma_yU^\dagger=\sigma_x\qquad U\sigma_xU^\dagger=-\sigma_z\] \[\sigma_x\rightarrow-\sigma_z,\sigma_y\rightarrow\sigma_x,\sigma_z\rightarrow-\sigma_y\]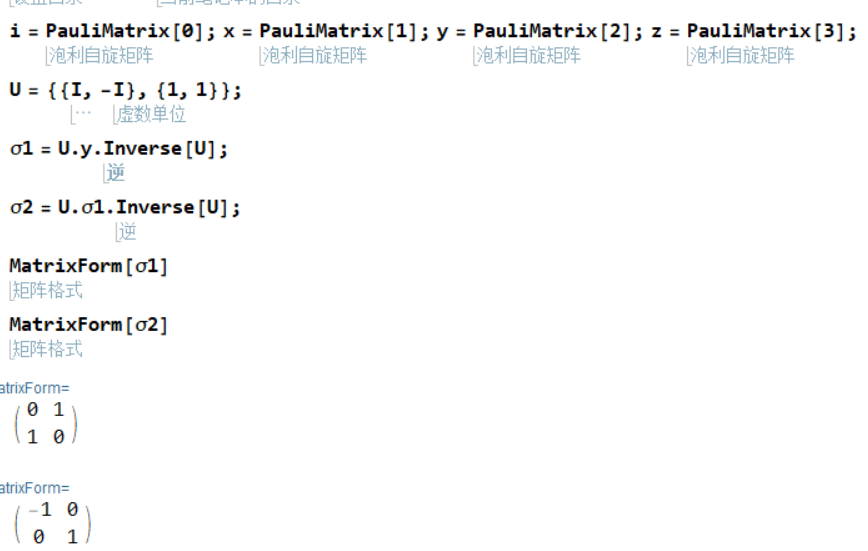
一般可以将这个幺正变换应用两次或者任意次数,来将不同的项放到不同的泡里矩阵前.
Edge mode and Dirac equation
这里整理一下通常拓扑绝缘体里面求解边界态的另外一种方法, 首先假设在$y$方向有质量的变化$m(y)$, 对于一个Chern insulator模型在低能下写成
\[H(y)=k_x\sigma_x+k_y\sigma_y+m(y)\sigma_z=-i\partial_x\sigma_x-i\partial_y\sigma_y+m(y)\sigma_z\]首先可以看到方程并没有$x,y$变量之间的耦合, 采用分离变量法, 假设方程的解为
\[\psi(x,y)=\phi_1(x)\phi_2(y)\]如果在$y$方向上存在质量畴壁, 那么存在的gapless边界态一定会是衰减形式的波函数, 且衰减长度与质量能隙$m(y)$有关
\[\phi_2(y)=e^{i\int_0^{+\infty}m(y^{'})dy^{'}}\]将假设的波函数代入薛定谔方程中
\[-i\partial_x\sigma_x\phi_1(x)+m(y)(i\sigma_y\phi_1(x)+\sigma_z\phi_1(x))=E\phi_1(x)\]对于零能解($k_x=0$), 其一定不存在与质量相关的依赖, 可以得到
\[i\sigma_y\phi_1(x)+\sigma_z\phi_1(x)=0\rightarrow \sigma_x\phi_1(x)=-\phi_1(x)\]方程的解为$\phi_1(x)=\xi(x)\frac{1}{\sqrt{2}}(1,-1)^T$, $\xi(x)$是个标量函数, 满足
\[i\partial_x\xi(x)=E\xi(x)\]解$\xi(x)=e^{ik_xx}$是一个在$x$边界上以能量$E=k_x$传播的手性模.
公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |