在学习时间反演不变拓扑绝缘体的时候,总是会遇到要计算$Z_2$拓扑不变量,但是其中会牵扯到Pfaffian这个概念,这里就整理一下反对称矩阵的Pfaffian到底和反对称矩阵之间有什么联系.

计算$Z_2$拓扑不变量的时候, 经常会遇到计算Pfaffian的计算, 这里就仔细从反对称矩阵出发, 学习整理一下Pfaffian对于反对称矩阵到底是怎样的一个概念.

反对称矩阵

如果$M$是一个$d\times d$维的复数反对称矩阵$M^T=-M^T$, 则可以有

\[\text{det}(M)=\text{det}(-M^T)=\text{det}(-M)=-(1)^d\text{det}(M)\]

从上面可以得到, 如果矩阵维度$d$是奇数, 那么一定会有$\text{det}(M)=0$, 因此矩阵$M$的秩一定是偶数$2n$, 如果$d\equiv2n$则$\text{det}(M)\neq 0$, 若$d>2n$则$\text{det}(M)=0$.

定理1 如果矩阵$M$是个非奇异的$2n\times 2n$维的复数(实数)反对称矩阵, 那么一定会存在一个$2n\times 2n$维的幺正矩阵$U$满足

\[U^TMU=N\equiv\text{diag}\left\{ \left(\begin{array}{cc}0&m_1\\ -m_1&0\end{array}\right),\left(\begin{array}{cc}0&m_2\\ -m_2&0\end{array}\right),\cdots,\left(\begin{array}{cc}0&m_n\\ -m_n&0\end{array}\right)\right \}.\]

这里矩阵$N$是由一系列$2\times 2$的分块矩阵构成的对角形式,$m_j$都是正实数. 而且$\text{det}(U)=e^{-i\theta},-\pi<\theta<\pi$. $N$被称为非奇异反对称矩阵的实正规形式.

如果$M$是一个$d\times d$秩为$2n$的奇异矩阵, 这里存在一个$d\times d$的幺正矩阵$U$

此时$N$写为对角形式后存在一些0元, 维度为$(d-2n)\times(d-2n)$.

定理2 如果$M$是个偶数维$2n\times 2n$的非奇异反对称复数矩阵, 存在一个非奇异$2n\times 2n$的矩阵$P$

\[M=P^TJP\]

这里$2n\times 2n$的矩阵$J$可以写成$2\times 2$矩阵的分块对角形式

\[U^TMU=N\equiv\text{diag}\left\{ \left(\begin{array}{cc}0&1\\ -1&0\end{array}\right),\left(\begin{array}{cc}0&1\\ -1&0\end{array}\right),\cdots,\left(\begin{array}{cc}0&1\\ -1&0\end{array}\right)\right \}. \label{eq1}\]

如果$M$是秩为$2n$维度为$d\times d$维的反对称奇异复矩阵, 存在一个非奇异的$d\times d$维的矩阵$P$

\[M=P^T\tilde{J}P\]

$\tilde{J}$的分块对角形式为

\[\tilde{J}\equiv\left(\begin{array}{cc}J&0\\0&0\end{array}\right)\]

这里$J$的形式如(\ref{eq1})所示.

Pfaffian

对于一个$2n\times 2n$偶数维的复反对称矩阵$M$, 定义矩阵$M$的Pfaffian为

\[\text{Pf}(M)=\frac{1}{2^nn!}\epsilon_{i_1j_1i_2j_2\cdots i_nj_n}M_{i_1j_1}M_{i_2j_2\cdots M_{i_nj_n}}\]

这里$\epsilon$是秩为2n的 Levi-Civita 张量, 重复指标代表求和. 如果让$P$表示${i_1,i_2,\cdots,i_n}$相对于${1,2,\cdots,2n}$的一系列置换

\[i_1\lt j_1,i_2\lt j_2,\cdots,i_{2n}\lt j_{2n}\qquad\text{and}\qquad i_1\lt i_2\lt\cdots\lt i_{2n}\label{eq2}\]

则可以将矩阵$M$的Pfaffian整理为

\[\text{Pf}(M)=\sum^{'}_P(-1)^PM_{i_1j_1}M_{i_2j_2}\cdots M_{i_nj_n}\label{eq3}\]

对于奇数次置换$(-1)^P=-1$, 对于偶数次置换$(-1)^P=1$. (\ref{eq3})求和中的上标则表示置换过程中满足(\ref{eq2})的限制. 如果矩阵$M$可以表示为分块对角直和形式$M\equiv M_1\oplus M_2=\text{diag}{M_1,M_2}$, 则矩阵的Pfaffian可表示为

\[\text{Pf}(M)=\text{Pf}(M_1)\oplus\text{Pf}(M_2)\]

相应的, 如果矩阵的维数是奇数, 那么其Pfaffian则为0.

定理3 对于任意$2n\times 2n$的复数矩阵$B$和$2n\times 2n$为的反对称矩阵$M$, 满足如下性质

\[\text{Pf}(BMB^T)=\text{Pf}(M)\text{det}(B)\]

定理4 如果$M$是一个复反对称矩阵, 则

\[\text{Pf}(M)^2=\text{det}(M)\]

程序计算

清楚了反对称矩阵的Pfaffian之后, 下面提供一个程序来计算一个反对称矩阵的Pfaffian, 代码是我从网上找的, 这里是Mathamatica的一个程序包, 需要调用才能使用, 具体如何安装一个Mathamtica的程序包, 可以参考空间群学习工具这篇博客中软件包的安装方法. 具体使用方法如下

png

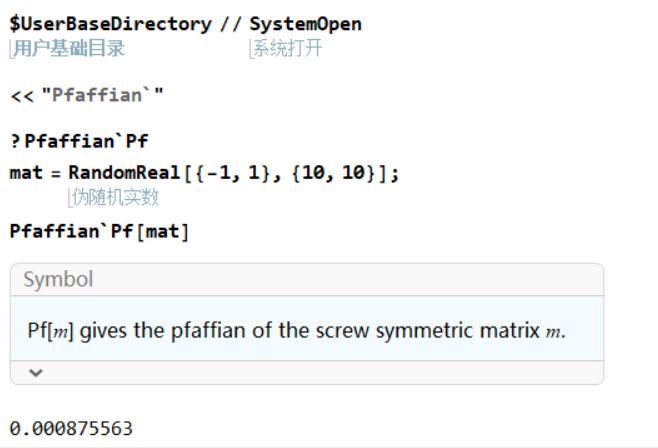
这个软件包可以点击这里下载

除了上面提到的程序包,还有一个比较系统计算Pfaffian的程序包,来源于Algorithm 923: Efficient Numerical Computation of the Pfaffian for Dense and Banded Skew-Symmetric Matrices这篇文章,程序包中包含了不同语言编写的计算Pfaffian程序

png