这篇博客从电荷极化的角度,更加物理的理解Hall电导与拓扑不变量对应的输运图像到底是怎么样对应起来的,同时也就理解了Chern数到底是怎样的一个物理对应.

虽然学习计算了许多的拓扑不变量, 但是一直没有一个清晰的物理图像来理解Chern数以及一些拓扑不变量到底是怎样的, 这里就整理一下电荷极化与拓扑不变量之间的联系,并理解其对应的物理实际.

这里先考虑最简单的一维链,其长度为$L$, 对于时间反演不变的体系, 占据态的数目一定是$2N$个, 占据态的波函数为

\[\rvert\psi_{n,k}\rangle=\frac{1}{\sqrt{L}}e^{ikx}\rvert u_{n,k}\rangle\]

与元胞波函数相关联的Wannier函数为

\[\rvert R,n\rangle=\frac{1}{2\pi}\int dk e^{-ik(R-r)}\rvert u_{n,k}\rangle\]

这里的$R$是实空间中的晶格矢量.

一维链中总的电荷极化等于所有占据态能带Wannier center的和

\[\begin{aligned}P&=\sum_n\int dr\langle 0,n\rvert r\rvert 0,n\rangle\\&=\sum_n\frac{1}{(2\pi)^2}\frac{1}{L}\int dr\int\int dk_1dk_2e^{i(k_1-k_2)r}\langle u_{n,k_1}\rvert r\rvert u_{n,k_2}\rangle\\&=\sum_n\frac{1}{2\pi}\int dk_xi\langle u_{n,k_x}\rvert\nabla\rvert u_{n,k_x}\rangle\end{aligned}\]

由于是一维体系,取$r=x$. 到这里可以将极化与Berry位相联系到一起

\[P=\frac{1}{2\pi}\int dk_xA(k_x),\qquad A(k_x)=i\sum_n\langle u_{n,k_x}\rvert\nabla_{k_x}\rvert u_{n,k_x}\rangle\]

极化中的积分是对于整个布里渊区进行的.作一个幺正变换$\rvert u(k)\rangle\rightarrow e^{i\phi}\rvert u(k)\rangle$, 这个$U(1)$规范变换将使得$k_x$在整个布里渊区增加$2\pi m$, 所以最终电荷极化变化为

\[P\rightarrow P+m\]

尽管极化不是规范不变的, 但是绝热连续的改变哈密顿量引起的电荷极化的变化量始终是规范不变的.假设哈密顿量依赖于一个外参量$k_y$变化, $H=H\left[k_y\right]$, 波函数$\rvert u_{k,n}(t)\rangle$在两个动量$K_{y1},K_{y2}$之间是连续的, 则有

\[P\left[K_{y2}\right]-P\left[K_{y1}\right]=\frac{1}{2\pi}(\int_{c2}dk_xA(k_x,k_y)-\int_{c1}dk_xA(k_x,k_y))\]

这里$c_{1,2}$是闭合的回路, 对于$k_y=K_{y1},K_{y2}$有$k_x=-\pi\rightarrow \pi$.利用Stokes定理将其改写为

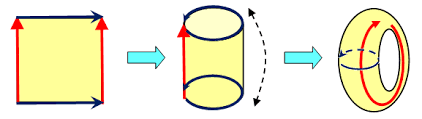
\[\int_{K_{y1}}^{K_{y2}}dk_y\int dk_xF(k_x,k_y)\] \[F(k_x,k_y)=i\sum_n(\langle\nabla_{k_x}u_{k_x,n}(k_y)\rvert\nabla_{k_x}u_{k_x,n}(k_y)\rangle-c.c)\]

此时的空间构型是个圆柱体$k_x$方向是周期的, $k_y$取值范围是$K_{y1}\rightarrow K_{y2}$, 且积分是对所有的占据态$n$求和.如果现在沿$y$方向同样取周期边界条件$K_{y1}=K_{y2}+2\pi$. 对于周期边界条件$H\left[k_y+2\pi\right]=H\left[k_y\right]$, 此时电荷极化的积分是在一个轮胎面上进行的, 他是一个闭合曲面, 这个计算量正好就对应着Chern数, 它代表着每个周期泵浦电子的差. 对于一个满足时间反演对称的体系而言$F(-k_x,-k_y)=-F(k_x,k_y)$, 所以此时Berry曲率的积分为0, 故而Chern数为0.

公众号

相关内容均会在公众号进行同步，若对该Blog感兴趣，欢迎关注微信公众号。