满足时间反演不变的体系, Chern数为0, 但是可以通过$Z_2$拓扑不变量描述, 任然可以通过一个物理图像来理解这个不变量和某一种极化之间的对应关系, 这里整理一下时间反演极化与$Z_2$拓扑不变量之间的联系.
虽然存在时间反演不变时, Berry曲率是个奇函数, 对BZ的积分为0, 但是任然可以通过$Z_2$拓扑不变量进行描述, 这里主要整理一下如何通过时间反演极化, 将一个具体的物理图像和$Z_2$拓扑不变量联系起来.
考虑一个1D能带结构, 它是具有$\frac{1}{2}$自旋满足时间反演对称的系统, 此时可以不用在考察整个BZ, 而只需要考虑半个BZ即可, 另外一半可以通过时间反演联系起来. 体系存在时间反演对称性时, 能带总是成对出现的, 系统整体的性质可以通过只考虑布里渊区中Kramers对中的一支即可.
时间反演对称将$k$的能带$\alpha$变换到$-k$的能带$\beta$,这里的$\alpha,\beta$是Kramers对,它们之间会相差一个位相因子
\[\rvert u^\alpha_{-k,a}\rangle=e^{i\chi_{k,a}}T\rvert u^\beta_{k,a}\rangle\label{2}\]时间反演操作算符$T$作用后
\[T\rvert u^\alpha_{-k,a}\rangle=Te^{i\chi_{k,a}}T\rvert u^\beta_{k,a}\rangle=e^{-i\chi_{k,a}}T^2\rvert u^\beta_{k,a}\rangle=-e^{-i\chi_{k,a}}\rvert u^\beta_{k,a}\rangle\]所以可以得到
\[\rvert u^\beta_{-k,a}\rangle=-e^{-i\chi_{-k,a}}T\rvert u^\alpha_{k,a}\rangle\]从上面可以看出, 在$\rvert u_{k,n}\rangle=\sum_mU_{mn}\rvert u_{k,m}\rangle$变换下它们并不是规范不变的表示,为了计算的目的, 将要找到一个规范不变的表示进行计算. 首先对时间反演不变Kramers对中的每一支来计算计算极化
\[P^s=\frac{1}{2\pi}\int_{-\pi}^{\pi}dkA^s(k)\qquad A^s(k)=i\sum_a\langle u^s_{k,a}\rvert\nabla_k\rvert u^s_{k,a}\rangle\qquad s=\alpha,\beta\]接下来将两支的极化联系起来
\[P^\alpha=\frac{1}{2\pi}\int_0^{\pi}(A^\alpha(k)+A^\alpha(-k))\]利用时间反演算符(\ref{2})可以得到
\[\begin{aligned}A^\alpha(-k)&=-i\sum_a\langle u^\alpha_{-k,a}\rvert\nabla_k\rvert u^\alpha_{-k,a}\rangle\\&=-i\sum_a\langle Tu^\beta_{k,a}\rvert\nabla_k\rvert Tu^\beta_{k,a}\rangle-i\sum_ai\nabla_k\chi_{k,a}\langle Tu^\beta_{k,a}\rvert Tu^\beta_{k,a}\rangle\\&=-i\sum_a\langle Tu^\beta_{k,a}\rvert\nabla_k\rvert Tu^\beta_{k,a}\rangle-i\sum_ai\nabla_k\chi_{k,a}\end{aligned}\] \[\begin{aligned}\langle Tu^\beta_{k,a}\rvert\nabla_k\rvert Tu^\beta_{k,a}\rangle&=(U_{mn}u^{\beta*}_{k,a,n})^{*}\nabla_k U_{mp}u^{\beta *}_{k,a,p}=(U^\dagger)_{mn}U_{mp}u^\beta_{k,a,n}\nabla_ku^{\beta *}_{k,a,p}\\&=u^\beta_{k,a,n}\nabla_ku^{\beta *}_{k,a,n}=-u^{\beta *}_{k,a,n}\nabla_k u^{\beta}_{k,a,n}=-\langle u^\beta_{k,a}\rvert\nabla_k\rvert u^\beta_{k,a}\rangle\end{aligned}\]综上可以得到
\[A^\alpha(-k)=i\sum_a\langle u^\beta_{k,a}\rvert\nabla_k\rvert u^\beta_{k,a}\rangle+\sum_a\nabla_k\chi_{k,a}=A^\beta(k)+\sum_a\nabla_k\chi_{k,a}\]可以得到极化为
\[\begin{equation}\begin{aligned}P^\alpha&=\frac{1}{2\pi}(\int_0^\pi(A^\alpha(k)+A^\beta(k))+\int_0^\pi\sum_a\nabla_k\chi_{k,a})\\&=\frac{1}{2\pi}(\int_0^\pi A(k)+\sum_a(\chi_{\pi,a}-\chi_{0,a}))\qquad A(k)=A^\alpha(k)+A^\beta(k)\end{aligned}\end{equation}\label{eq2}\]最后一项可以通过$U(2N)$的sewing matrix进行改写
\[B_{mn}=\langle u_{-k,m}\rvert T\rvert u_{k,n}\rangle\]这里$\rvert u_{\pm k,m}\rangle$代表的是所有的占据态,利用关系式
\[\rvert u^\alpha_{-k,a}=e^{i\chi_{k,a}}T\rvert u^\beta_{k,a}\rangle,\rvert u^\beta_{-k,a}\rangle=-e^{i\chi_{-k,a}}T\rvert u^\alpha_{k,a}\rangle\]得到
\[B^{\beta,\alpha}_{mn}(k)=\langle u^\beta_{-k,m}\rvert T\rvert u^\alpha_{k,n}\rangle=-\delta_{mn}e^{-i\chi_{-k,n}},B^{\alpha,\beta}_{mn}=-B^{\beta,\alpha}_{mn}(-k)\]$B^{\beta,\alpha}_{mn}$是Kramers对能带$\alpha,\beta$的sewing matrix,这里可以存在多个Kramers对$m=1,2,\cdots,N$, 但是sewing matrix 耦合Kramers对是两两组合的, 所以矩阵$B$将会变成分块非对角形式
\[B=\left[\begin{array}{cc}0&-e^{-i\chi_{-k,n}}\\e^{-i\chi_{k,n}}&0\end{array}\right]\label{eq7}\]可以看到在$k=0,\pi$处, 矩阵$B$是反对称的, 故而可以将(\ref{eq2})中的第二项改写为
\[\sum_a(\chi_{\pi,a}-\chi_{0,a})=i\text{log}\left[\frac{\text{Pf}[B(\pi)]}{\text{Pf}[B(0)]}\right]\]对于能带$\alpha$的极化
\[P^\alpha=\frac{1}{2\pi}(\int_0^\pi dk A(k)+i\text{log}\left[\frac{\text{Pf}[B(\pi)]}{\text{Pf}[B(0)]}\right])\]将能带$\alpha,\beta$的极化叠加起来, 就可以得到整体的极化
\[P=\frac{1}{2\pi}\int_{-\pi}^\pi dk A(k)=P^\alpha+P^\beta\]正如前面提及到的, 满足时间反演不变的体系, 对应的Chern数为0, 所以此时两个能带的极化总和也为0, 但是可以定义时间反演极化$P^T=P^\alpha-P^\beta=2p^\alpha-P$
\[P^T=\frac{1}{2\pi}(\int_0^\pi dk A(k)-\int_{-\pi}^0dk A(k)+2i\text{log}[\frac{\text{Pf}[B(\pi)]}{\text{Pf}[B(0)]}])\label{eq6}\]此时体系的时间反演极化不为零, 可以作为拓扑不变量与实际物理图像之间的联系来理解体系的拓扑性质.
非阿贝尔贝利位相
时间反演操作可以将$\rvert u_{k,\beta}\rangle$与另外一个动量为$-k$的简并态联系起来,如果系统同时存在反演对称性, 则在每个$k$点能带都是双重简并的
\[\rvert u_{-k,\alpha}\rangle=\sum_\beta B^{*}_{\alpha,\beta}(k)T\rvert u_{k,\beta}\rangle\label{eq4}\]这里的$\alpha,\beta$是能带index,矩阵$B$是幺正矩阵
\[\langle u_{-k,\alpha}\rvert T\rvert u_{k,\beta}\rangle\qquad B_{\alpha\beta}(k)=-B_{\beta\alpha}(-k)\]对于多带系统,non-Abelian Berry vector为
\[\begin{aligned}a^{\alpha\beta}_i(-k)&=i\langle u_{-k,\alpha}\rvert\partial_{k_i}\rvert u_{-k,\beta}\rangle\\&=-i\sum_{m\theta\gamma}B_{\theta\gamma}(k)B^{*}_{\beta\gamma}(k)(u_{k\theta})_nU^{*}_{mn}U_{mp}\partial_k(u_{k\gamma})^{*}_p+B_{\alpha\theta}(k)(\partial_kB^{*}_{\beta\gamma}(k))(u_{k\theta})_nU^{*}_{mn}U_{mp}(u_{k\gamma})^{*}_n\\&=-i\sum_{n,\theta,\gamma}N_{\alpha\theta}(k)B^{*}_{\beta\gamma}(k)(u_{k\theta})_n\partial_k(u_{k\gamma})^{*}_n-B_{\alpha\theta}(k)(\partial_kB^{*}_{\beta\gamma})(u_{k\theta})_n(u_{k\gamma})^{*}_n\\&=B_{\alpha\theta}(k)(-i(u_{k\theta})_n\partial_k(u_{k\gamma})^{*}_n)B^{*}_{\beta\gamma}-iB_{\alpha\theta}\partial_kB^{*}_{\beta\theta}\end{aligned}\]上式推导将(\ref{eq4})代入即可, 最终得到$-k$处的非阿贝尔矢势是$k$处非阿贝尔矢势的复共轭,再加上一个矩阵$B$的规范变换
\[a^{\alpha\beta}_i(-k)=B_{\alpha\theta}(k)a^{\theta\gamma *}_i(k)B^{*}_{\beta\gamma}-B_{\alpha\theta}\partial_kB^{*}_{\beta\theta}\qquad a_i(-k)=B(k)a^{*}_i(k)B^\dagger(k)-iB\partial_iB^\dagger\]阿贝尔Berry位相是非阿贝尔势的对角元素
\[\begin{aligned}A_i(-k)=\text{Tr}[a_i(-k)]&=\text{Tr}[B^\dagger(k)B(k)a_i^*(k)]-\text{Tr}[iB\partial_iB^\dagger]\end{aligned}\]$k,-k$点的Abelian矢势的差为
\[\text{Tr}[B^\dagger(k)\partial_kB(k)]=\frac{1}{i}(A_i(-k)-A_i(k))\label{eq5}\]结合(\ref{eq5})可以将(\ref{eq6})改写为
\[\begin{aligned}P^T&=\frac{1}{2\pi}(\int_0^\pi dk A(k)-\int_{-\pi}^0dk A(k)+2i\text{log}[\frac{\text{Pf}[B(\pi)]}{\text{Pf}[B(0)]}])\\&=\frac{1}{2\pi i}(\int_0^{\pi} dk\text{Tr}[B^\dagger\partial_kB]-2\log[\frac{\text{Pf}[B(\pi)]}{\text{Pf}[B(0)]}])\end{aligned}\]结合(\ref{eq7})可得
\[\begin{aligned}\text{Tr}[B^\dagger\partial_kB]&=\text{Tr}[\left[\begin{array}{cc}0&-e^{-i\chi_{-k,n}}\\e^{-i\chi_{k,n}}&0\end{array}\right]\left[\begin{array}{cc}0&-\nabla_ke^{-i\chi_{-k,n}}\\\nabla_ke^{-i\chi_{k,n}}&0\end{array}\right]]\\&=-i(\nabla_k\chi_k+\nabla_k\chi_{-k})=\nabla_k\log(\text{Det}[B(k)])\end{aligned}\]最终时间反演极化可以表示为
\[p_T=\frac{1}{2\pi}(\int_0^{\pi}dk\nabla_k\log[\text{Det}[B(k)]]-2\log[\frac{\text{Pf}[B(\pi)]}{\text{Pf}[B(0)]}])\]因为矩阵$B$是反对称的, 根据反对称矩阵Pfaffian学习中的内容, 可以知道$\text{Det}[B]=\text{Pf}[B]^2$, 则时间反演极化为
\[P_T=\frac{1}{\pi i}\log[\frac{\sqrt{\text{Det}[B(\pi)]}}{\text{Pf}[B(\pi)]}\frac{\text{Pf}[B(0)]}{\text{Det}[B(0)]}]\]因为取对数的不确定性, $P_T$仅对2的余数有意义$(P_T\quad\text{mod}\quad 2)$, 也就是说对于一个规范变换, 只会改变$P_T$偶数的值. $P_T$的奇偶性则决定于在$k=0,\pi$处$\text{Pf}(B(k))$与$\sqrt{\text{Det}(B(k))}$处于相同的分支还是不同的分支.
Wannier Center
当系统存在时间反演的时候,占据的Wannier轨道的中心也会随着外部参数的变化而改变,相比较于Chern insulator,此时Wannier态是成对出现的,如果体系是$Z_2$非平庸的,那么在时间演化的过程中这一对Wannier center会彼此交换位置.
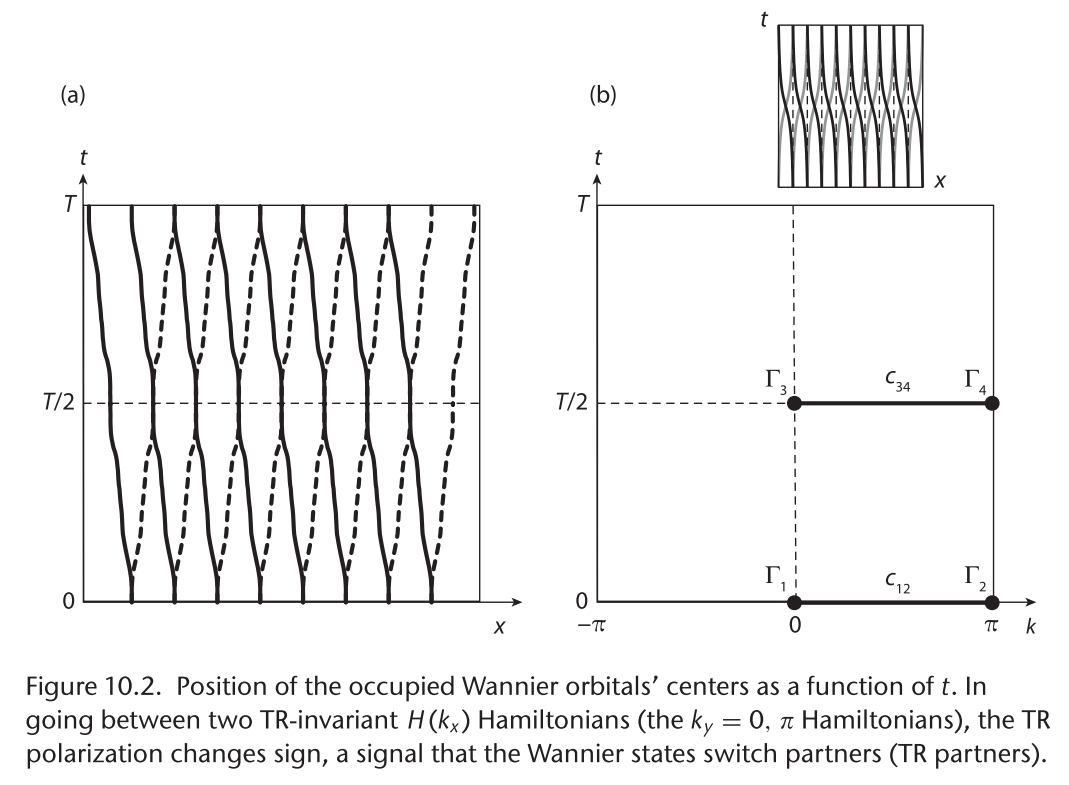
如果时间反演极化在$t=0$和$t=T/2$的差为1, 则它们之间存在一个不匹配的性质, 此时一定会有奇数条边界态在$t=0$与$t=T/2$之间穿过费米能级,对应的拓扑不变量为
\[P_T(T/2)-P_T(0)=P_T(k_y=\pi)-P_T(k_y)=0\]当系统维度是2维的时候,上式等于
\[\Pi_{i=1}^4\frac{\sqrt{\text{Det}[B(\Lambda_i)]}}{\text{Pf}[B(\Lambda_i)]}\]此处的$\Lambda_i$是2D布里渊区中的时间反演不变动量点.
对于三维的体系
\[Z_2=\Pi_{i=1}^8\frac{\sqrt{\text{Det}[B(\Lambda_i)]}}{\text{Pf}[B(\Lambda_i)]}\]$\Lambda_i$是3D布里渊区中的8个时间反演不变动量点.
\[\Lambda_i=\{(0,0,0),(0,0,\pi),(0,\pi,0),(0,\pi,\pi),(\pi,0,0),(\pi,0,\pi),(\pi,\pi,0),(\pi,\pi,\pi)\}\]公众号
相关内容均会在公众号进行同步,若对该Blog感兴趣,欢迎关注微信公众号。

|
yxli406@gmail.com |